tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

12 = 3×4, 56 = 7×8

数学 整数論 日曜数学 12 = 3×4, 56 = 7×8

こんにちは、tsujimotterです。

まずはこちらのツイートをご欄ください。


特に読んでいただきたいのは、藤坂一麦さんのプロフィールにあるこの一行です。

2008年頃　　　　１２＝３×４，５６＝７×８の美しさに感動する


つまり

12 = 3\times 4 \tag{1}
56 = 7\times 8 \tag{2}

のような式が成り立つというお話です。

1から8まで順に並んでいる のが面白いですね。このような式は、ほかにもあるのでしょうか？

f:id:tsujimotter:20190910220045p:plain:w300



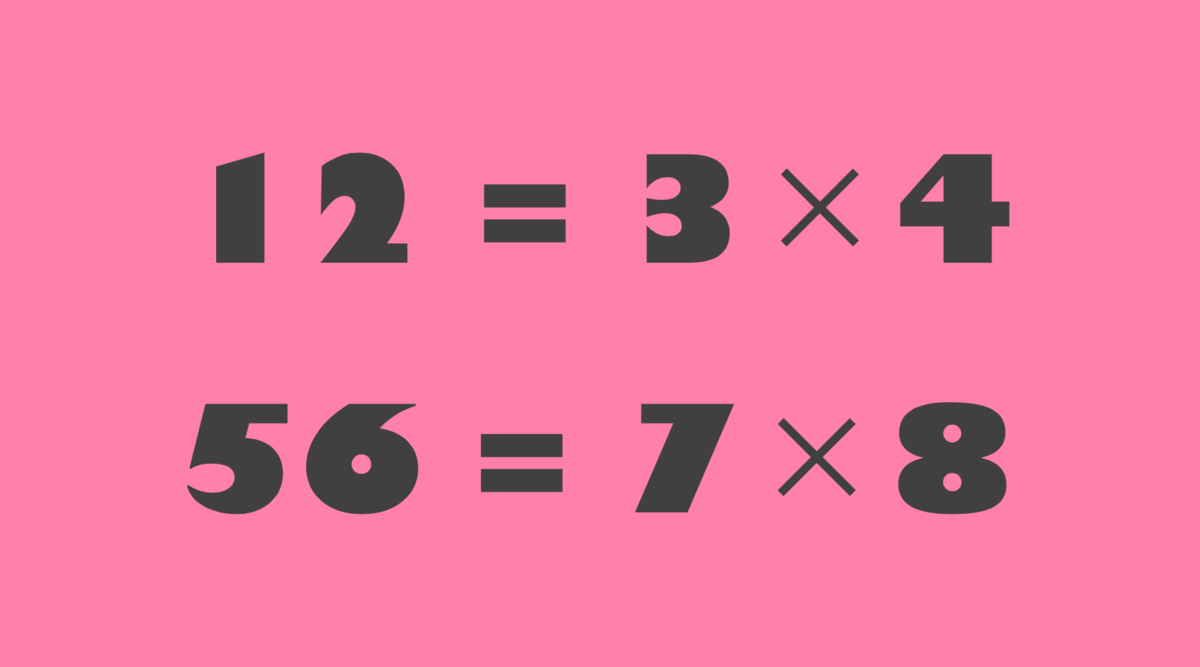
というわけで、今日はこんな問題を考えてみたいと思います。

n 進法で ab と書かれた数が、 c \times d と表せるとします。ただし、 a, b, c, d はそれぞれ n 進法の１桁の数で表される数で、 b, c, d は b = a + 1, \; c = a + 2, \; d = a + 3 を満たすとします。

このとき、正の整数 n, a を求めよ。

上の例は10進法でしたが、10進法にこだわる必要はないので、一般の n 進法で考えてみたいと思います。

今回の問題は、高校数学の範囲で解ける問題となっています。よかったら、ぜひ一度自分で考えてみてください。藤坂さんの感動を追体験できるかもしれません。

続きを読む

10/19,20に #マスパーティ を開催します！

イベントレポート 数学 日曜数学

日曜数学者のtsujimotterこと辻順平です。普段は、趣味で数学を勉強し、その成果を楽しく伝える活動をしています。

この度、2019年10月19日（土）・20日（日）の２日間、30時間ぶっ通しで数学の企画を行うというイベント マスパーティ を、横浜市鶴見周辺で開催することになりました。
mathparty.localinfo.jp

主催はキグロさんと私です。キグロさんは、2015年の第１回日曜数学会から４年間に渡って一緒に日曜数学会を主催している仲間です。この２名のほかに、数学カフェやロマンティック数学ナイトプライムなど、これまで交流を深めてきた各種の数学イベントの主催者の面々が加わり、一丸となって準備を進めております。

一昨日、マスパーティの企画の全容が情報解禁となりました。このタイミングで、マスパーティ開催に至った経緯やコンセプトの紹介、マスパーティの楽しみ方などを書いてみたいと思います。

この記事を読んで「マスパーティ楽しそうだな」「参加してあげてもいいかな」と思った方、あるいは記事に共感してくださった方がいましたら、ぜひお集まりいただけたら嬉しいなと思います。

続きを読む

ヘロンの三角形と連分数

数学 整数論

今日の話題は、数学のお兄さんこと横山明日希さんによるこちらのツイートから。

辺の長さが整数723、724、725で構成される正三角形に近い三角形の面積は、なんと整数226974になる

三角形の3辺 723, 724, 725はすべて整数で、かつ、面積も整数です。

「こんな三角形どうやって見つけるの？」

というのが今日のテーマです。


実は、連分数 を使うと見つけることができます。これが今日一番の面白ポイントです。

tsujimotterはちょうど最近、連分数にはまっていまして、その意味でもグッドなタイミングでこのお話を知ることができました。

よろしければお付き合いください。

続きを読む

3次方程式の判別式

数学 代数学

n 次多項式

f(X) = a_n X^n + a_{n-1} X^{n-1} + \cdots + a_2 X^2 + a_1 X + a_0

を考えるとき、方程式 f(X) = 0 の判別式とは、 n 個の解 \alpha_1, \alpha_2, \ldots, \alpha_n を用いて

\displaystyle \Delta = a_n^{2n-2} \prod_{i < j}(\alpha_i - \alpha_j)^2

と表せる量のことです。


たとえば、3次方程式 f(X) = X^3 + pX + q = 0 を考えて、その3つの解を \alpha, \beta, \gamma とするとき

\displaystyle \Delta = (\alpha - \beta)^2(\beta - \gamma)^2(\gamma - \alpha)^2

と表すことができますね。要するに、すべての解の差をとり、2乗して掛け合わせたものですね。

定義から明らかなように、 f(X) が重根を持つなら判別式は 0 となります。つまり、判別式は重根の存在の判定器になっているということですね。ほかにも判別式にはいろいろな面白いことがありますが、今日は深入りはしません。


さて、今日はこの3次方程式の判別式を計算したいと思います。

続きを読む

モジュラー曲線(4)：レベル構造付き楕円曲線とモジュライ空間

数学 モジュラー曲線 楕円曲線

前回の記事では、モジュラー曲線 Y(1) と楕円曲線の同型類全体が全単射であることを示しました。すなわち、 Y(1) は楕円曲線の（同型類の）モジュライ空間になっているということでした。
tsujimotter.hatenablog.com


今回はレベル構造が入ったモジュラー曲線 Y_1(N) を考えたいと思います。このモジュラー曲線は一体何のモジュライ空間なのかというのが今回の主題です。

実は、上の話の類似で、 Y_1(N) はレベル構造が付いた楕円曲線のモジュライ空間になっています。今日はそれを示すのを目的とします。

続きを読む

モジュラー曲線(3)：複素トーラスとしての楕円曲線

数学 楕円曲線 モジュラー曲線

今回の記事は、楕円曲線についての基礎的な事項についてのおさらいです。

これまでのtsujimotterのノートブックでは、色々な記事で楕円曲線について紹介してきました。しかしながら、どれも文字数や手間の関係で駆け足で紹介せざるを得ませんでした。ここで一度腰を据えて丁寧に解説したいと思います。

楕円曲線は、代数曲線としての側面を紹介することが多いですが、今回は複素トーラスとしての側面について中心に紹介します。これは、後でモジュラー曲線に関する記事で使うことを想定しています。

モジュラー曲線関連の情報は、以下のタグの一連の記事でまとめているところです。
tsujimotter.hatenablog.com

なお、今回の記事はモジュラー曲線に関するシリーズ記事の一環で書いていますが、今回の記事に関して言えば、これまでの知識なしで読めるものとなっています。

続きを読む