続々・12 = 3×4, 56 = 7×8 - tsujimotterのノートブック

前々回の記事で、 $ab = c\times d$ 型の問題に対して

$ab = d\times e \times f \tag{1}$

$abc = d\times e \times f \tag{2}$

という拡張が考えられるという話をしました。

式 $(2)$ の方は前回の記事で扱ったので、今回は式 $(1)$ を解いてみたいと思います。

つまり、今回の問題はこれです。

正の整数 $n, a$ が $a + 4 < n$ と、次の式を満たすとする：

$an + (a+1) = (a+2) (a+3) (a+4) \tag{3}$

このとき、 $n, a$ の組を求めよ。

今回の問題は比較的簡単で、 $ab = c\times d$ 型の問題とほぼ同様の手順で計算することができます。やってみましょう。

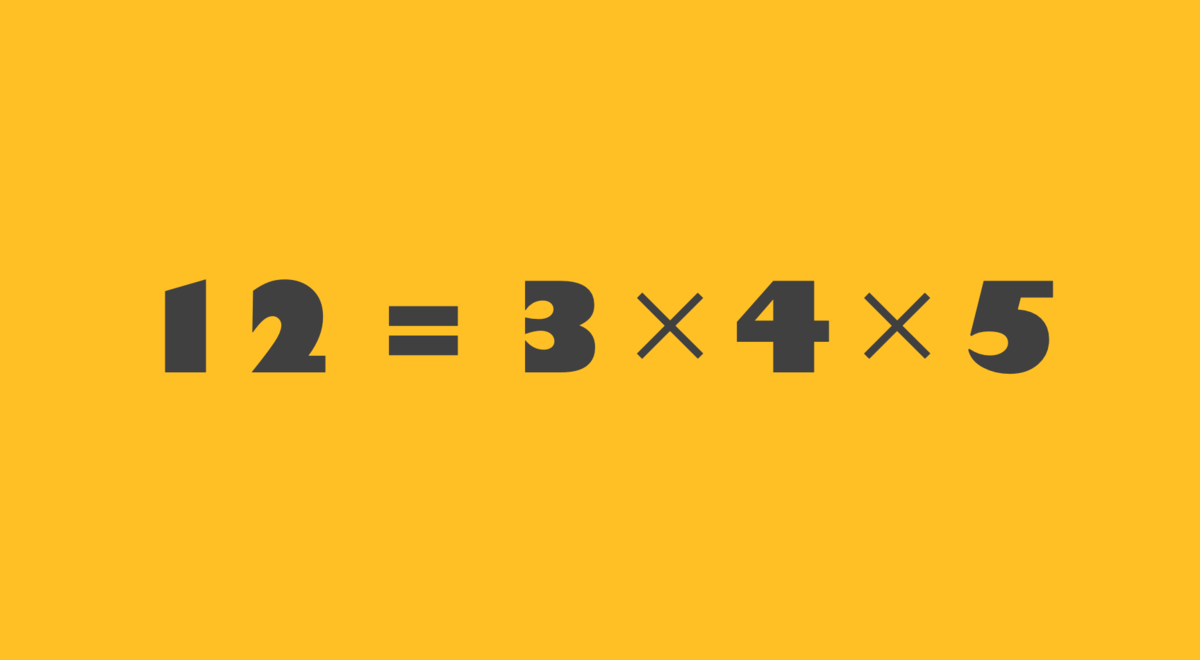
f:id:tsujimotter:20190911185603p:plain:w300

おまけとして、後半では右辺が $k$ 個になったバージョンも考えたいと思います。

解答例

式 $(3)$ を変形します。

$\begin{align} an + a + 1 &= (a + 2)(a + 3)(a + 4) \\ &= a^3 + 9a^2 + 26a + 24 \end{align}$

右辺の計算をするときのコツなんですが、次の対称式の基本定理を使うと簡単に計算できます。（このやり方はunaoyaさんに教えていただきました）

$(x + \alpha)(x + \beta)(x + \gamma) = x^3 + (\alpha + \beta + \gamma)x^2 + (\alpha \beta + \beta \gamma + \gamma \alpha)x + \alpha \beta \gamma$

さて、前々回の記事で行ったように、移項して右辺に定数項を持ってきて、左辺を $a$ で括ります。

$a(n+1-a^2-9a-26) = 23$

ここでまた整数論的な考察を使います。

右辺の約数は $1$ と $23$ で、左辺も同様です。したがって、 $a = 1$ または $a = 23$ となります。

あとは、それぞれの場合で計算すればOKです。

$a = 1$ のとき、 $n+1-a^2-9a-26 = 23$ となりますが、 $n$ について計算すると

$\begin{align} n &= 23 - 1 + a^2+9a+26 \\ &= 23 - 1 + 1+9+26 \\ &= 58 \end{align}$

よって、 $a = 1, \; n = 58$ が１つめの整数解となります。

$a = 23$ のとき、 $n+1-a^2-9a-26 = 1$ となりますが、 $n$ について計算すると

$\begin{align} n &= 1 - 1 + a^2+9a+26 \\ &= 23^2+9\cdot 23+26 \\ &= 762 \end{align}$

よって、 $a = 23, \; n = 762$ が１つめの整数解となります。

以上、２つの解

$a = 1, \; n = 58 \tag{4}$

$a = 23, \; n = 762 \tag{5}$

が求める整数解であることがわかりました。（終わり）

つまり、こういうこと

以上２つが求める整数解だったわけですが、これはどういうことでしょうか。

$(ab)_{n} = c\times d\times e$ の形に直すと、式 $(4)$ は

$(12)_{58} = 3\times 4\times 5$

となります。これは、 $58$ 進法で $12$ と表される数は、 $3\times 4\times 5$ に一致するということですね。たしかに計算するとそうなっています。

もう一つの解 $(5)$ も $(ab)_{n} = c\times d\times e$ の形に直したいのですが、各桁の数字が2桁以上になってしまいます。桁の区切りを ";" で無理やり表すと

$(23; 24)_{762} = 25\times26\times 27$

というような書き方になりますが、 $10$ 進法になれた我々にとってはやや難しいですね。 $762$ 進法をうまく表現するためには、762種類の数字が必要です。

一方で、時間を表現するために、我々は60進法を使っています。時計のアナロジーで考えてみましょう。

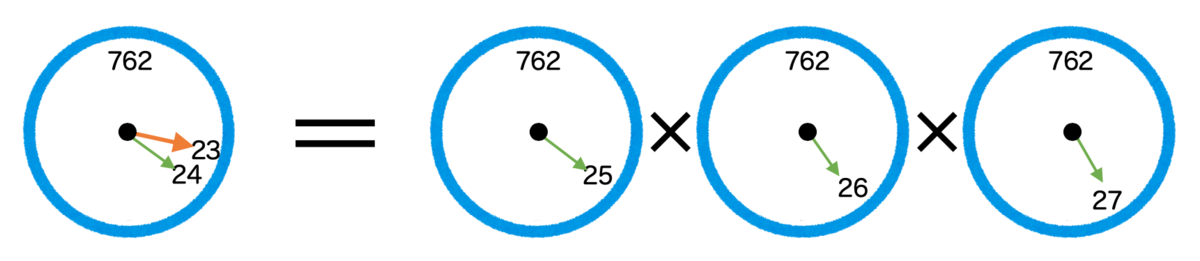
1時間が $762$ 分で、1分が $762$ 秒であるような時計を考えます。そのような時計において、 $23$ 分 $24$ 秒は一体何秒かという問題を考えると、その答えが $25\times 26\times 27$ 秒である、ということですね。図に表すとこんな感じです。

f:id:tsujimotter:20190911185459p:plain:w500

さらなる拡張

ここまでくると、右辺を $k$ 個の積にしたとしても、同様の計算ができることに気づきます。

$an + (a+1) = \underbrace{(a+2) (a+3) \cdots (a+k+1)}_{k \, \text{times}} \tag{6}$

ここで、右辺は $\{2, 3, \ldots, k+1\}$ の $i$ 次基本対称式 $\sigma_i$ を用いて

$a^k + \sigma_1 a^{k-1} + \cdots + \sigma_{k-1} a + \sigma_{k}$

と表せます。定数項の $\sigma_k$ は

$\sigma_k = 2\cdot 3\cdot \cdots \cdot (k+1) = (k+1)!$

と表せることに注意すると、式 $(6)$ は

$a(n + 1 - a^{k-1} - \sigma_1 a^{k-2} - \cdots - \sigma_{k-1}) = (k+1)! - 1$

と表せます。

$k = 3$ のときは、定数項が $(3+1)! - 1 = 23$ だったわけですね。

上の問題と同じように、 $(k+1)! - 1$ の約数を考える必要があります。これについての一般論は難しいので、 $(k+1)! - 1$ の約数の一つを $d$ として考えましょう。

すると、 $a = d$ と書くことができ

$\displaystyle n + 1 - a^{k-1} - \sigma_1 a^{k-2} - \cdots - \sigma_{k-1} = \frac{(k+1)! - 1}{d}$

と表せます。

もちろん、ここから $n = \cdots$ のように整理してもいいですが、もう少し簡単に考えましょう。

元々は式 $(6)$ からスタートしたわけなので、 $(6)$ に $a = d$ を代入してもよいわけですね。よって

$dn + (d+1) = \underbrace{(d+2) (d+3) \cdots (d+k+1)}_{k \, \text{times}}$

が成り立ちます。ここで、 $n$ 以外の項を右辺に持っていき、 $d$ で割ると

$\displaystyle n = \frac{\underbrace{(d+2) (d+3) \cdots (d+k+1)}_{k \, \text{times}} - (d+1)}{d}$

となります。また、よくよく考えると

$\underbrace{(d+2) (d+3) \cdots (d+k+1)}_{k \, \text{times}} = (d+k+1)! / (d+1)!$

とかけますから、よりすっきり

$\displaystyle n = \frac{(d+k+1)! / (d+1)! - (d+1)}{d}$

と表すことができます。

よって一般解は、 $(k+1)! - 1$ の約数を $d$ として、次のように得られることがわかりました。

$\begin{cases} \displaystyle a = d \\ \displaystyle n = \frac{(d+k+1)! / (d+1)! - (d+1)}{d} \end{cases}$

a = 1 のケース

$1$ は必ず $(k+1)! - 1$ の約数になりますので、次のタイプの式は、任意の $k$ に対して存在します。

$(12)_n = \underbrace{3 \times 4 \times \cdots \times (k+2)}_{k\, \text{times}}$

このときの $n$ は

$\displaystyle n = (k+2)! / 2 - 2$

と表せます。せっかくなので、いくつかの $k$ について計算してみましょう。

$\begin{align} (12)_{58} &= 3 \times 4 \times 5 \\ (12)_{358} &= 3 \times 4 \times 5 \times 6 \\ (12)_{2518} &= 3 \times 4 \times 5 \times 6 \times 7 \\ (12)_{20158} &= 3 \times 4 \times 5 \times 6 \times 7\times 8 \\ (12)_{181438} &= 3 \times 4 \times 5 \times 6 \times 7\times 8\times 9 \end{align}$

まとめ

これまでの結果をまとめておきましょう。

問題	解
$ab = c\times d$ 型	$\begin{align} (12)_{10} &=3\times 4, \\ (56)_{10} &=7\times 8 \end{align}$
$ab = c\times d\times e$ 型	$\begin{align} (12)_{58} &=3\times 4\times 5, \\ (23; 24)_{762} &=25\times 26 \times 27 \end{align}$
$a_1 a_2$ $= \underbrace{a_3 \times a_4 \times \cdots \times a_{k+2}}_{k\, \text{times}}$ 型	$(k+1)!-1$ の任意の約数 $d$ に対して $(d; d+1)_{n} = \prod_{i=2}^{k+1} (d+i)$ （ただし、 $n = \frac{(d+k+1)! / (d+1)! - (d+1)}{d}$ ）
$abc = d\times e$ 型	なし
$abc = d\times e\times f$ 型	なし