tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

続・12 = 3×4, 56 = 7×8

数学整数論日曜数学 12 = 3×4, 56 = 7×8

前回に引き続き、 $12 = 3\times 4$ 関連の問題を考えたいと思います！　前回の記事を読んでいない方は、ぜひ読んでみてください：
tsujimotter.hatenablog.com

前回はロマンティック数学ナイトの登壇者・藤坂さんのツイートをきっかけに、 $12 = 3\times 4$ というタイプの式は、 $56 = 7\times 8$ の他には存在しないということについて考察しました。

今回は、この問題を拡張して

$123 = 4\times 5\times 6$

のタイプの問題を考えてみたいと思います！

f:id:tsujimotter:20190910230133p:plain:w300

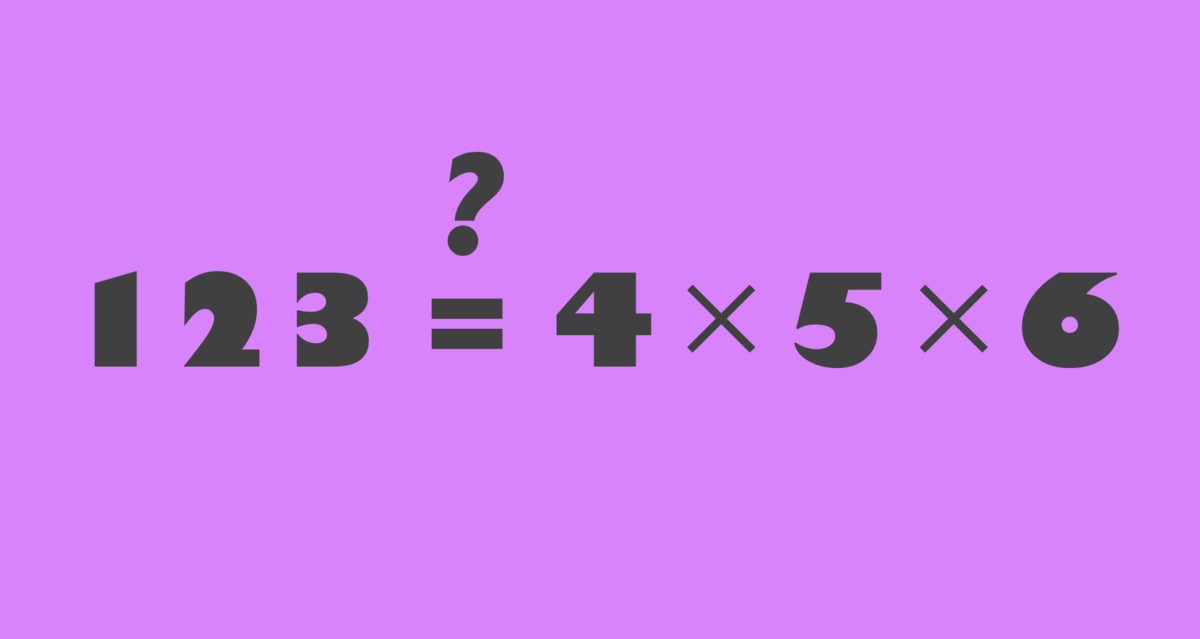
もちろん、上のような式は（少なくとも10進法では）成り立ちません。実際に考えたいのは次の問題です。

正の整数 $n, a$ が $a + 5 < n$ と、次の式を満たすとする：

$an^2 + (a+1)n + (a+2) = (a+3) (a+4) (a+5) \tag{1}$

このとき、 $n, a$ の組を求めよ。

この問はtsujimotterには解けなかったのですが、Twitterで声をかけてみたところ、みうらさん（@miura_prime）という方がその日のうちに解いてくださいました！
解法がとても興味深かったので、今回はそれをご紹介したいと思います。自分で考えてみたいという方は、スクロールを止めて、ぜひ考えてみてください。

解答例

まず $n > a+5$ なので、正の整数 $k$ を用いて $n = a + k$ と表すと $k > 5$ となることがわかります。

その $k$ を用いて、式 $(1)$ に $n = a + k$ を代入します。

$a(a+k)^2 + (a+1)(a+k) + (a+2) = (a+3) (a+4) (a+5) \tag{2}$

これで、変数は $a, k$ だけになりました。

さらに式 $(2)$ の(左辺) $-$ (右辺)を、関数 $F_k(a)$ で表すことにします。

$F_k(a) := a(a+k)^2 + (a+1)(a+k) + (a+2) - (a+3) (a+4) (a+5) \tag{3}$

$F_k(a) = 0$ となるような $a, k$ が元の問題の解を与えるというわけです。

ここで $k \geq 9$ のとき、 $F_k(a)$ は実際には正の値をとってしまう、という補題を示したいと思います。すなわち、この条件では解がないということです。

補題

$a, k$ を正の整数とする。 $k \geq 9$ のとき、 $F_k(a) > 0$ が成り立つ。

（補題の証明） $F_k(a)$ を次のように変形する。

$\begin{align} F_k(a) &= a(a+k)^2 + (a+1)(a+k) + (a+2) - (a+3) (a+4) (a+5) \\ &= a^3 + (2k + 1)a^2 + (k^2 + k + 2)a + (k + 2) - a^3 - 12a^2 - 47a - 60 \\ &= (2k - 11)a^2 + (k^2 + k - 45)a + k - 58 \end{align} \tag{4}$

ここで、 $F_k(a)$ は $a$ についての 2次関数になっていることに注意します（3次の項が消えた！）。

$k \geq 9$ のとき、 $F_k(a)$ の2次の項と1次の項の係数は

$2k - 11 > 0$

$k^2 + k - 45 > 0$

となることがわかります。したがって、 $F_k(a)$ は $a > 0$ のとき単調増加します。

ここで $k \geq 9$ のとき、 $a = 1$ を計算すると

$\begin{align} F_k(1) &= (2k - 1) + (k^2 + k - 45) + k - 58 \\ &= k^2 + 4k - 114 \\ & \geq 9^2 + 4\cdot 9 - 114 \\ & > 0 \end{align}$

となります。

したがって、 $F_k(a) > 0$ が言えました。（補題の証明終わり）

図に表すとこういう感じです。横軸が $a$ で赤い線が $F_k(a)$ です。 $k \geq 9$ のときに $F_k(1) > 0$ であることが確認できるかと思います。

k ≧ 9 のときに a ≧ 1 における F_k(a) の値が正になることをグラフで示す（訂正版） pic.twitter.com/VgkxQuQp5E
— tsujimotter (@tsujimotter) September 10, 2019

以上により、 $k$ として考えるべき範囲は $5 < k < 9$ のとき、すなわち

$k = 6, 7, 8$

の 3通りであることがわかりました。

あとは、この3通りすべてを調べればよいでしょう！

$k = 6$ のとき

式 $(4)$ に $k = 6$ を代入すると

$F_6(a) = a^2 - 3a - 52$

です。方程式 $F_6(a) = 0$ の判別式は

$3^2 + 4\cdot 52 = 217 = 7\times 31$

で、平方数ではないので、 $a$ は整数ではありません。

$k = 7$ のとき

式 $(4)$ に $k = 7$ を代入すると

$F_7(a) = 3a^2 + 11a - 51$

です。方程式 $F_7(a) = 0$ の判別式は

$11^2 + 4\cdot 3\cdot 51 = 733$ （素数）

で、平方数ではないので、 $a$ は整数ではありません。

$k = 8$ のとき

式 $(4)$ に $k = 8$ を代入すると

$F_8(a) = 5a^2 + 27a - 50$

です。方程式 $F_7(a) = 0$ の判別式は

$27^2 + 4\cdot 5\cdot 50 = 1729 = 7 \times 13 \times 19$

で、平方数ではないので、 $a$ は整数ではありません。

以上から、すべての $k > 5$ なる $k$ に対して、条件を満たす整数 $a$ は存在しないことがわかります。

よって、式 $(1)$ には条件を満たす整数解がないことが示されました。（終わり）

やりましたね！　お疲れさまでした！

おわりに

以上の考察により、

$123 = 4\times 5 \times 6$

というタイプの式は存在しないということが証明できました！

証明の流れも面白かったですね。 $n = a + k$ と置くことで $a$ の2次関数にできること、そして、十分大きな $k$ では左辺の方が大きくなってしまい解がないことを示す、という方針が鮮やかでした。

無事解決できてよかったです！

この問題に取り組んだきっかけは、藤坂さんによる「１２＝３×４，５６＝７×８の美しさに感動する」という一文からでした。どんな感動があるのだろうと思って前回の問題に取り組んだわけですが、おかげさまでとても興味深いに出会うことができました。

まだまだ拡張はできそうな問題ですので、興味がある方はぜひ取り組んでみてください。

それでは、今日はこの辺で。

続きはこちら！

tsujimotter.hatenablog.com