tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

12 = 3×4, 56 = 7×8

数学整数論日曜数学 12 = 3×4, 56 = 7×8

こんにちは、tsujimotterです。

まずはこちらのツイートをご欄ください。

【8/24ロマンティスト紹介その６】

藤坂一麦

2001年5月28日数学の存するこの世界に生まれる
2008年頃　　　　１２＝３×４，５６＝７×８の美しさに感動する
2015年頃　　　　三角関数のテイラー展開の神秘に涙を流す
2019年現在　　　愚直に数学を愛する#ロマンティック数学ナイト pic.twitter.com/asNMvZmz8W
— ロマンティック数学ナイト (@r_mathnight) August 8, 2019

特に読んでいただきたいのは、藤坂一麦さんのプロフィールにあるこの一行です。

2008年頃　　　　１２＝３×４，５６＝７×８の美しさに感動する

つまり

$12 = 3\times 4 \tag{1}$

$56 = 7\times 8 \tag{2}$

のような式が成り立つというお話です。

1から8まで順に並んでいるのが面白いですね。このような式は、ほかにもあるのでしょうか？

f:id:tsujimotter:20190910220045p:plain:w300

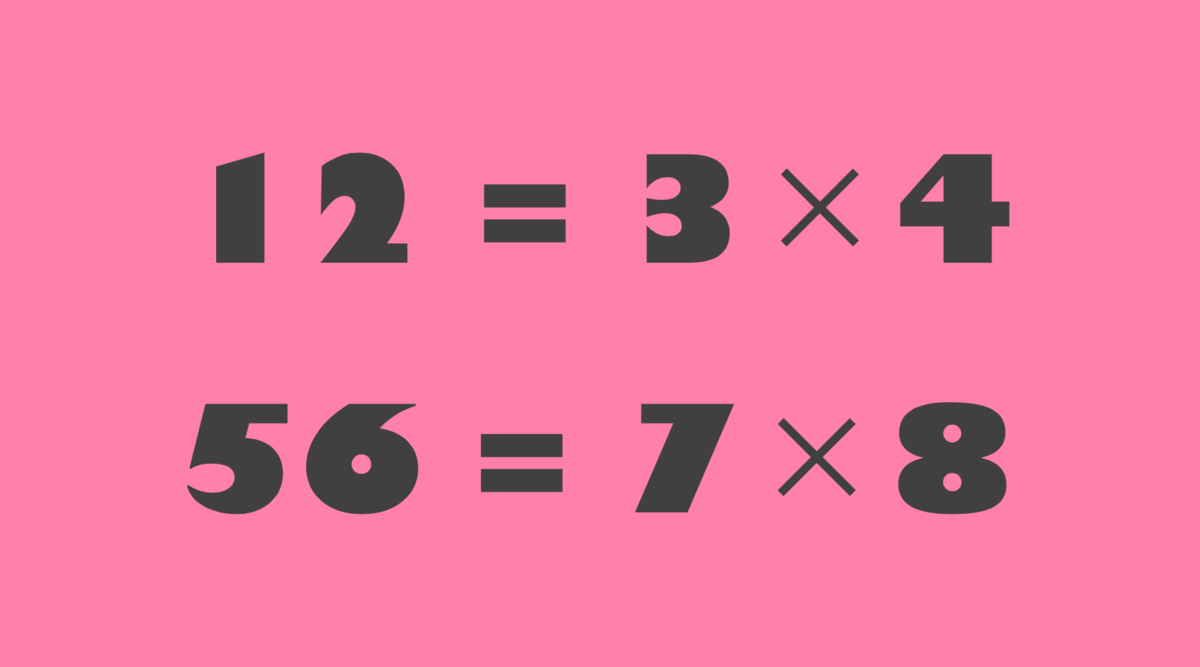
というわけで、今日はこんな問題を考えてみたいと思います。

$n$ 進法で $ab$ と書かれた数が、 $c \times d$ と表せるとします。ただし、 $a, b, c, d$ はそれぞれ $n$ 進法の１桁の数で表される数で、 $b, c, d$ は $b = a + 1, \; c = a + 2, \; d = a + 3$ を満たすとします。

このとき、正の整数 $n, a$ を求めよ。

上の例は10進法でしたが、10進法にこだわる必要はないので、一般の $n$ 進法で考えてみたいと思います。

今回の問題は、高校数学の範囲で解ける問題となっています。よかったら、ぜひ一度自分で考えてみてください。藤坂さんの感動を追体験できるかもしれません。

問題の言い換え

まずは、問題を言い換えるところから始めましょう。

$n$ 進法で $(ab)_{n}$ と表せる数は、以下のように表されるのでした。

$(ab)_{n} := an + b$

これは、10進法の数 $(12)_{10}$ が

$(12)_{10} := 1\cdot 10 + 2$

とかけるのと同じことです。

そこで、上の問題は次のように言い換えられます。

$n > a + 3$ であるような正の整数 $n, a$ が次の式を満たすとする：

$an + (a+1) = (a+2) \times (a+3) \tag{3}$

このとき、 $n, a$ の組を求めよ。

解答例

それでは、解答を考えてみましょう。

式 $(3)$ を計算します。

$an + a+1 - a^2 - 5a - 6 = 0$

$an - a^2 - 4a - 5 = 0$

定数項とそれ以外で分離して、 $a$ で括ります。

$a(n - a - 4) = 5$

ここで整数論的なテクニックを使います。ここが今回のポイントです。

右辺の $5$ の約数は $1$ か $5$ ですから、左辺全体の約数も $1$ か $5$ です。

左辺は $a$ と $(n - a - 4)$ の積の形になっていますから、 $a = 1$ または $a = 5$ が成り立ちますね。

$a = 1$ のとき $n - a - 4 = 5$ となり、 $n = 10$ が成り立ちます。

また、 $a = 5$ のとき $n - a - 4 = 1$ となり、こちらも $n = 10$ となります。

したがって、2つの整数解

$a = 1, n = 10$

$a = 5, n = 10$

が得られました。整数解はこれで全部です。

つまりこういうこと

上の１つめの解

$a = 1, n = 10$

は元の式に代入すると

$12 = 3\times 4$

になります。また、２つめの解

$a = 5, n = 10$

は元の式に代入すると

$56 = 7\times 8$

となります。

つまり、元々の２つの式で解はすべて出尽くしていたいうことですね！　他の式は存在しなかったと！

このように考えると、今回の式に対する藤坂さんの感想も納得いきますね。他には存在しないということが示せたわけですから。たしかに美しい。

さらにいえば、私の解法では、10進法に限らない一般の $n$ 進法でも考えていたわけですが、なぜか解は $n = 10$ のときにしかありませんでした。

普通この手の問題を考えると、10進法に限らず解があるものなのですが、10進法にしか解がないというのは興味深いですね！

数が協力して、指が10本ある人間という生物に発見してもらいたがっているような、そんな感じさえします。

次の問題は？

一度このような問題を考えると、さらに一般化したくなってきますね。

元々の問題は、左辺が２桁の数で、右辺は１桁の数２個の積となっていましたが、桁数や積の個数を変えたらどうなるでしょうか。

たとえば、左辺が３桁の場合を考えてみましょう。

右辺は１桁の数２個の積だったとすると、

$an^2 + (a+1)n + (a+2) = (a+3)(a+4)$

の解を求めることになります。 $a, a+1, a+2, a+3, a+4$ は1桁の数なので、 $n > a+4$ が条件です。

この問題については、少しの考察によって解がないことがわかってしまいます。

左辺は明らかに $n^2$ より大きいわけですが、右辺は $n$ より小さい2つの数の積なので $n^2$ より小さくなるからです。

よって、問題を拡張するためには、右辺の積の個数を3つ以上にする必要があるでしょう。これついては、次回の記事で考えたいと思います。

お楽しみに！

それでは、今日はこの辺で。

2019/09/11 追記

書いたあとで思い出したのですが、左辺が2桁で右辺が1桁3つの積というパターンもありました。

$an + (a+1) = (a+2)(a+3)(a+4)$

こちらも同様の方針で考えることができますので、興味がある人は考えてみてください！

続きはこちら！

tsujimotter.hatenablog.com