「統計的決定理論」とは何か?はじめてこの名前を聞いた方も多いかと思います。まずはざっくりと統計的決定理論について説明してみましょう。
統計的決定理論とは、
「うーん、あっちが良いかもしれないなあ。いや、こっちかなあ。」
と決めかねているときに、
「男ならウダウダ軟弱なこと言ってないで一点に決めてみろ。」
と背中を押してくれる理論のことです。
単に背中を押すだけでなく、1つの答えを決定するための指針と方法を与えてくれます。男前な理論ですね。
とはいえ、この説明ではいったい何のことだか、よくわからないですよね(笑)
以下では、真面目に統計的決定理論について説明てみたいと思います。ちょっと長いですが、お付き合い頂けるとうれしいです。
1. 統計的決定とは
ある確率分布にしたがう確率変数 θ を統計的に「妥当な」一点 α に決めるとき、この α を統計的決定といいます。
たとえば、θ の確率分布を示す確率密度関数を f(θ) としたとき、その f(θ) が平均 μ 、分散 σ^2 の正規分布であった場合、θ の推定値は f(θ) の平均値、すなわち、μ をとれば「文句はなさそう」です。
この場合の統計的決定は α = μ ということになります。

では、この f(θ) が一般の確率密度関数だった場合はどうでしょう。
f(θ) の平均値が「良い」ですか?次のような分布だったら、たしかに平均が「良さそう」です。
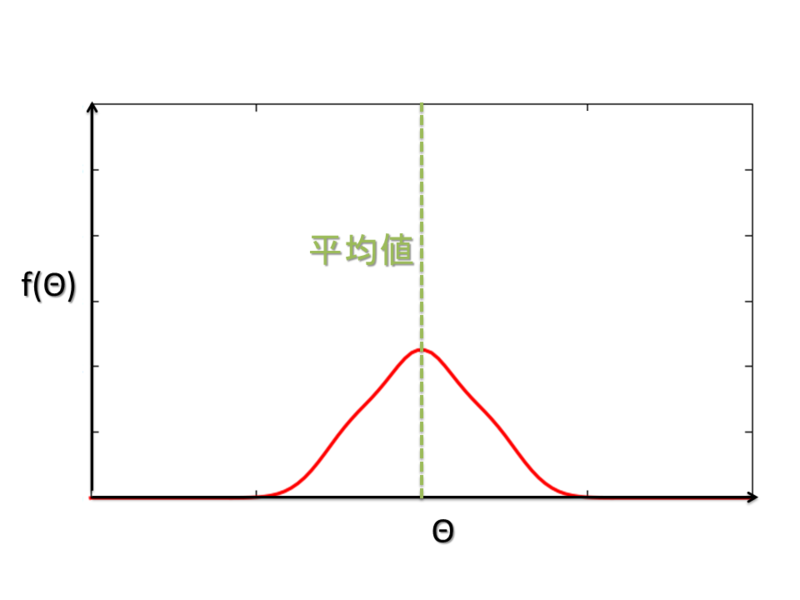
一方で、たとえばこんな分布だったらどうでしょう。
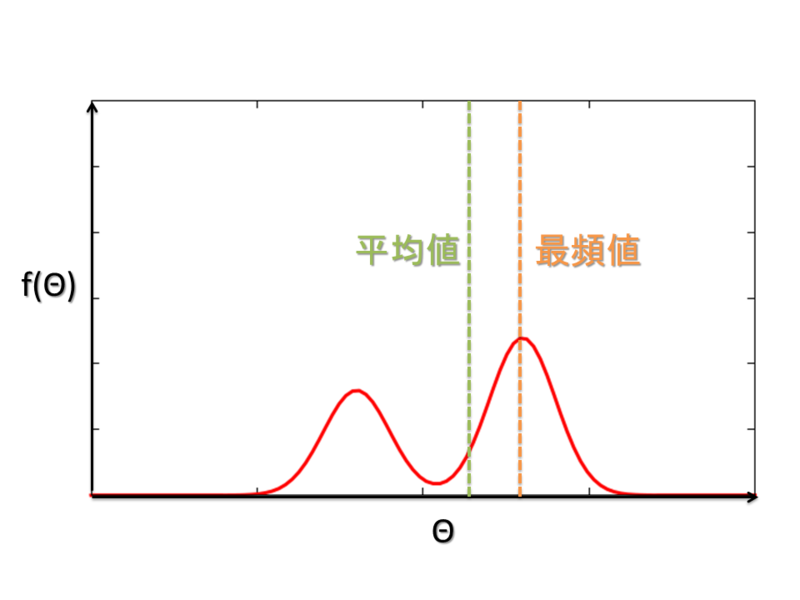
平均値は、ちょうど二つの山の間となってしまい、どっちつかずの印象ですね。むしろ、右の大きな山の頭のあたりを取ったほうが、まだ「良さそう」な気がします。こういう値を最頻値といいますね。
そもそも、統計的決定の「良さ」とはなんでしょうか。この「良さ」の基準を定量的に考え、最適な統計的決定を求めること。これこそが統計的決定理論の趣旨であり、私たちが学ぶべきことと言えます。
2. 損失関数
統計的決定理論においては、統計的決定の「良さ」を表す基準として、損失関数 (loss function) を導入します。損失関数は、確率変数 θ と 統計的決定 α を引数とした関数で、α と θ に差があったときに、その差に応じて 「損失」 の大きさが決まるものです。実際の値 θ と その決定 α に差があるほど「損失」が大きいと考え、その損失を最小化する統計的決定を考えたいわけです。
具体的な損失関数は、たとえば次のようなものを考えます。
a. 平方損失
b. 絶対損失
c. 0-1型単純損失
統計的決定理論では、損失関数の期待値(以下、期待損失)が小さいほど「良い」統計的決定と考えます。θ はあくまで確率変数ですから、たった一回の計測で得られた θ を基に α の良し悪しを評価しても仕方ありませんね。だから期待値をとるのです。つまり、最適な統計的決定とは「期待損失を最小化するような α である」ということです。
確率変数 θ が確率密度関数 f(θ) に基づいて発生するとき、統計的決定 α の期待損失は
期待損失を最小化する α が、(確率密度関数 f(θ) にしたがう) θ に対する最良の統計的決定となります。すなわち、
一般に、損失関数が定まったときの最適な統計的決定は、解析的に求められる場合もあれば、そうでない場合もあります。興味深いことに、上記で挙げた3つの損失関数に対しては、統計的決定が解析的に計算できるのです。以下で実際に計算してみましょう。
3. 平方損失の場合
として、R(α)を計算すると
ここで、∫f(θ)dθ は全θに対する確率密度関数の和であるため、確率の定義より ∫f(θ)dθ=1 となります。また、∫θf(θ)dθ は 確率密度関数 f(θ) に従う確率変数 θ の期待値ですから ∫θf(θ)dθ = E[θ] です。
よって、
つまり、平方損失における最良の統計的決定は 確率分布 f(θ) の平均値ということがわかりました。
結論1:平均値は、平方損失の期待損失を最小化する
たしかに直感的にはそんな感じがしますが、平均値という値に「平方損失最小化」という意味が付くというのは非常に面白いですね!
4. 絶対損失の場合
として、R(α)を計算すると
平方損失のときと同様に α で微分して、イコール 0 として極値を求めましょう。
よって
これで求める式は得られたのですが、パッと見て意味はわかりづらいですね。
図で考えましょう。
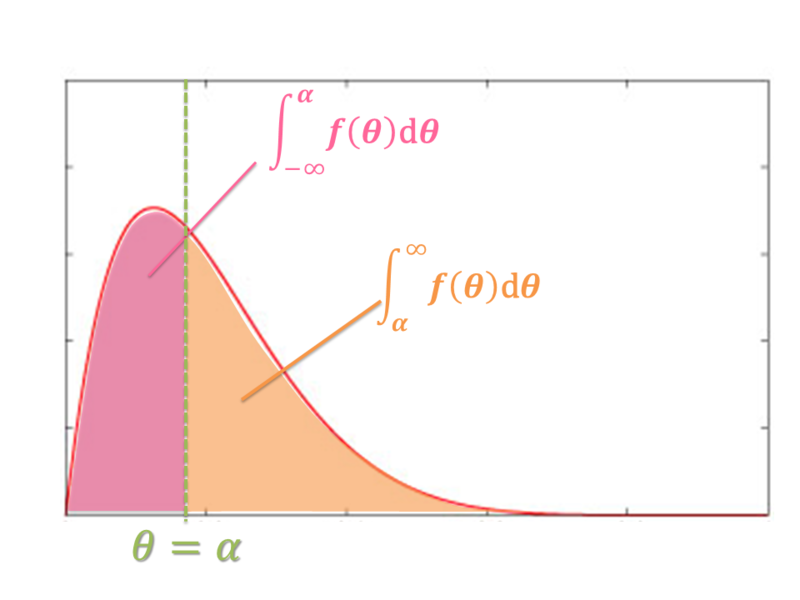
左側の面積と右側の面積が等しいということです。αで確率密度関数の面積を均等に分割していますから、このαは分布の中央値を表していますね。
これより 絶対損失における 統計的決定 α は f(θ) の中央値であるいうことがわかります。
結論2:中央値は、絶対損失の期待損失を最小化する
中央値も出てきました!最後に、0-1型単純損失の場合はどうでしょうか。
5. 0-1型単純損失
として、R(α)を計算すると
十分小さな Δ に対しては右辺の積分は
と f(α) に比例するとみなせます。(2Δを一辺とする縦長の長方形を考えてみてください。)
よって、R(α) を最小化するためには、f(α) を最大化すればよいことがわかります。
f(α) を最大化するαは最頻値ということですね。
したがって、0-1型単純損失における統計的決定 α は f(θ) の最頻値を取ればいいことがわかります。
結論3:最頻値は、0-1型単純損失の期待損失を最小化する
6. まとめ
以上をまとめると、次のようになります。

今回は、統計的決定理論に基づいて平方損失・絶対損失・0-1型単純損失のそれぞれに最適な統計的決定を求めました。その結果として、それぞれの損失関数に対応して、統計的な分布を代表する値(代表値)の3つである平均値・中央値・最頻値が得られました。
今回の結果から逆説的に、今回のサブタイトルでもある「平均値・中央値・最頻値の意味」を考えることもできるでしょう。これらは、平方損失・絶対損失・0-1型単純損失の3つの期待損失をそれぞれ最小化する値だったのです。
男には決断しなきゃいけない時があります。決断に困ったら確率分布とお好みの損失関数を用意してください(笑)。
参考文献
以下の本の第二章を参考に書いています。非常にわかりやすい本なので、よかったら読んでみてください。
[1] 松原望 著「入門ベイズ統計―意思決定の理論と発展」東京図書 (2008年)

- 作者: 松原望
- 出版社/メーカー: 東京図書
- 発売日: 2008/06
- メディア: 単行本
- 購入: 107人 クリック: 2,061回
- この商品を含むブログ (46件) を見る
追記
統計的決定理論は英語でStatistical Decision Theoryといいます。この記事を書くためにいろいろ調べたのですが、日本語も英語もなかなかちゃんと書いてある記事がない。
もちろん、「平方損失・絶対損失・単純損失に対応して、平均値・中央値・最頻値が導かれるという事実」までは書いてあるのですが。それ自体はWikipediaにも書いてあったりしますね。
しかしながら、どの記事にも肝心の導出が書かれていない。そこが一番面白いところなのに!(と思いませんか?)
上記の文献にも平方損失の導出まではちゃんと書いてありますが、中央値に関しては結果しか書かれていません。
その後、かなり探して次の文献を見つけましたので、ここに記しておきます。ちゃんと証明が載っています。
また、統計的決定は「ベイズ決定」とも呼ばれているそうですね。ベイズ推定の結果は「事後確率」という分布でしか表せないので、具体的な推定値を求めるためには統計的決定が必須なのです。