twitterで面白い問題を教えてもらったので、紹介します。
数学好きの人はぜひチャレンジしてみてください。
続き。「1/12377の小数点以下第6193桁目の数は何になるか?」は数年前にオープンキャンパスで出した問題。ヒント無しですぐに答えられる人はすごいと思う。こういう算数の問題の背後に平方剰余の相互法則のような貴重で美しい数学の話が隠れている。
— 黒木玄 Gen Kuroki (@genkuroki) 2014年2月16日
方法として考えられるのは、実直に 6193桁 まで計算することでしょう。
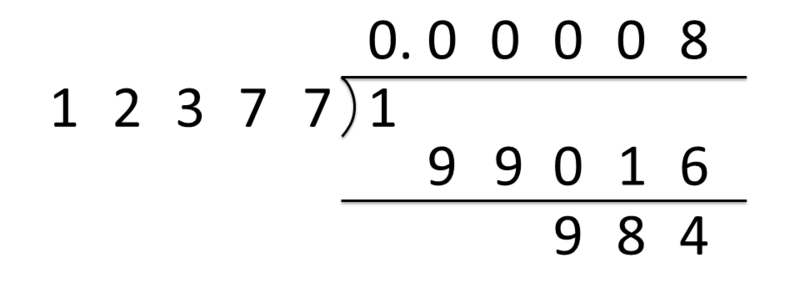
しかし、当然この方法ではあまりに時間がかかりすぎますし、たぶん間違えます。
このツイートにあるように、この問題は「平方剰余の相互法則」という法則を使うことで エレガントに解くことが出来ます。
次回、解答編です!
謝辞・参考文献
なお、解答は @genkuroki さんの下記サイトの下部「オープンキャンパス2009年の数学クイズ」に掲載されています。こちらには高校生向けの解答も載っていますので、ぜひご参照ください。
次回以降の私の記事は @genkuroki さんからいただいたヒントを元に、証明を含めて具体的に書く予定です。
@genkuroki さんのツイートがなければ、このような興味深い問題に出会うことがなかったと思います。
心よりお礼申し上げます。
循環小数問題1/12377の小数点以下6193桁目は何か?(問題編) - tsujimotterのノートブック
1/12377の小数点以下6193桁目は何か?(解答編) - tsujimotterのノートブック第1回:循環小数(1): フェルマーの小定理 - tsujimotterのノートブック
解説編
第2回:循環小数(2): Midyの定理(前編) - tsujimotterのノートブック
第3回:循環小数(3): Midyの定理(後編) - tsujimotterのノートブック
第4回:循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック