1/12377の小数点以下6193桁目は何か？（解答編）

前回の記事：
1/12377の小数点以下6193桁目は何か？（問題編） - tsujimotterのノートブック

問題はこれでした。

続き。「1/12377の小数点以下第6193桁目の数は何になるか？」は数年前にオープンキャンパスで出した問題。ヒント無しですぐに答えられる人はすごいと思う。こういう算数の問題の背後に平方剰余の相互法則のような貴重で美しい数学の話が隠れている。
— 黒木玄 Gen Kuroki (@genkuroki) 2014年2月16日

f:id:tsujimotter:20140408161339p:plain:w300

もし、自分で問題を解きたいと思っている方がいましたら、前回の記事に戻ってみてください。

「もうギブアップ」あるいは「解答を確認したい」という方は、↓に進んでください。

解答

まず次の定理を使います。

$p$ を 2, 5以外の素数とし、 $1/p$ の小数点以下 $k$ 桁目を $a_k$ とする。
1. $p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ のとき
$a_{(p-1)/2+k} = a_k$

2. $p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ 以外のとき
$a_{(p-1)/2+k} = 9 - a_k$

ここで $p=12377$ より、

$12377 \equiv 17 \pmod{40}$

から、上記の 2. に該当する。

したがって、

$a_{6193} = 9 - a_5$

である。

ここで $1/12377$ の循環節の前半は、

$1/12377 = 0.0000807...$

だから、

$a_5 = 8$

よって、

$a_{6193} = 9 - 8 = 1$

解答：
$1/12377$ の小数点以下 $6193$ 桁目の数は $1$ である。

念のためプログラムを書いて確認してみました。

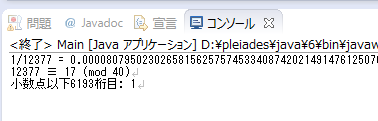
たしかに、 $1$ になっていますね。

次回予告

たしかに答えは出たのですが、どうもすっきりしないな、と思った方がいるかと思います。

なにしろ私もそうでした。

真っ先に思う疑問はなぜ 40 で割った余りが関係あるのでしょう。

そして、なぜ $a_k$ は $(p-1)/2$ を境に前後で関係し合うのでしょう。

次回以降では、 $p$ を素数としたときの循環小数 $1/p$ について、謎を解き明かしていきたいと思います。

まず第１回は、大前提として、循環小数は $(p-1)$ 桁で循環するという基本的な性質を紹介します。

第２回、第３回では、Midyの定理と呼ばれる、循環小数を半分の $(p-1)/2$ 桁で分けたときの前後の関係について紹介します。

第４回がメインディッシュです。なぜ $40$ で割った余りなのか。これは、整数論の花形である「平方剰余の相互法則」が見事に関係してきます。

それでは、お楽しみに！

循環小数問題

1/12377の小数点以下6193桁目は何か？（問題編） - tsujimotterのノートブック
 1/12377の小数点以下6193桁目は何か？（解答編） - tsujimotterのノートブック

解説編

第１回：循環小数(1): フェルマーの小定理 - tsujimotterのノートブック
第２回：循環小数(2): Midyの定理（前編） - tsujimotterのノートブック
第３回：循環小数(3): Midyの定理（後編） - tsujimotterのノートブック
第４回：循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック