循環小数(3): Midyの定理（後編） - tsujimotterのノートブック

循環小数問題

1/12377の小数点以下6193桁目は何か？（問題編） - tsujimotterのノートブック
 1/12377の小数点以下6193桁目は何か？（解答編） - tsujimotterのノートブック

解説編

第１回：循環小数(1): フェルマーの小定理 - tsujimotterのノートブック
第２回：循環小数(2): Midyの定理（前編） - tsujimotterのノートブック
第３回：循環小数(3): Midyの定理（後編） - tsujimotterのノートブック
第４回：循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック

本記事は、循環小数問題の解説編として書いています。

第３回は Midyの定理（後編）として、前回示したMidyの定理を使って循環小数の後半の値を推定する方法を紹介します。

Midy の定理の復習とその応用

《定理２（Midyの定理 [Midy, 1836]）》
p を 2, 5 以外の素数とし、循環小数 1/p の循環節の長さが偶数になるとき、その循環節を前後で２分割した数の和は必ず 9999.....999 の形をした数となる。

あとで使いやすいようにするために、次の等価な表現に変えておきましょう。

《Midyの定理の言い換え》
$p$ を 2, 5 以外の素数とし、循環小数 $1/p$ の小数点以下 $k$ 桁目を $a_k$ 、循環節の長さを $e$ とする。
$e$ が偶数のとき、次が成り立つ。

$a_{e/2+k} + a_k = 9$

実はこの定理は、循環小数の後半の桁の値を推測するのに使えるのです。

たとえば、1/17の小数点以下第 9 桁の値は、1/17 の循環節の長さが 16 であることを知ってさえいれば容易にわかります。

やってみましょう。

1/17 の場合

$1/17$ の循環節の長さが 16 であると仮定します。このとき、Midyの定理の言いかえを用いると、

$a_{16/2+1} + a_1 = 9$

ここで $a_1$ は、計算するまでもなく 0 とわかりますから、逆に $a_{16/2+1}$ 、すなわち小数点以下 9 桁目は 9 と即座にわかるのです。

なかなか面白いでしょう。

循環節の長さと (p+1)/2 桁目の値の推定

こうなってくると、任意の素数 $p$ おける $1/p$ の循環節の長さがどうなるか気になってきますね。

正確にいうと、今回の話に限れば、循環節の長さがわからなくても「循環節の長さが $(p-1)/2$ の約数になっているかどうか」がわかればよいのです。

図を見ながら解説しましょう。

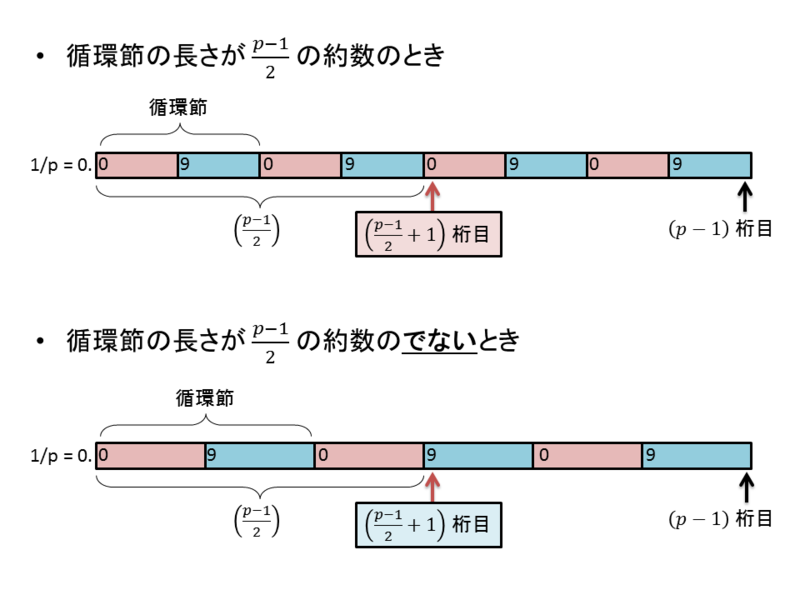
循環節の長さが $(p-1)/2$ の約数になっているときは、 $(p-1)/2$ で循環しますから、 $\frac{(p-1)}{2}+1=\frac{p+1}{2}$ の地点は小数点以下 1桁目が登場するはずです。したがって、素数 p が 2桁以上の場合は、必ず 0 になります。

一方で、循環節の長さが $(p-1)/2$ の約数でないときは、 $(p-1)/2$ 桁で循環しません。しかしながら、 $(p-1)/2$ の地点では（何巡目かはわかりませんが）循環節の前半の終わりがきます。したがって、 $\frac{(p-1)}{2}+1=\frac{p+1}{2}$ の地点では、後半戦の一番最初の桁が登場します。したがって素数 p が 2桁以上の場合は Midyの定理より 9 が登場することがわかってしまいます。

まとめ

以上をまとめると次のようになります。

《定理３》
$p$ を 2, 5 以外の素数とする。 $1/p$ の循環節の長さを $e$ 、小数点以下 $k \left(\leq \frac{e}{2}\right)$ 桁目を $a_k$ とすると、
1. $e$ が $\left(\frac{p-1}{2}\right)$ の約数であるとき

$a_{(p-1)/2+k} = a_k$

2. $e$ が $\left(\frac{p-1}{2}\right)$ の約数でないとき

$a_{(p-1)/2+k} = 9 - a_k$