循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック

循環小数問題

1/12377の小数点以下6193桁目は何か？（問題編） - tsujimotterのノートブック
 1/12377の小数点以下6193桁目は何か？（解答編） - tsujimotterのノートブック

解説編

第１回：循環小数(1): フェルマーの小定理 - tsujimotterのノートブック
第２回：循環小数(2): Midyの定理（前編） - tsujimotterのノートブック
第３回：循環小数(3): Midyの定理（後編） - tsujimotterのノートブック
第４回：循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック

（※ $p$ は以下、断りなく 2, 5 以外の素数として扱います。）

本記事は、循環小数問題の解説編として書いています。

今回が、私がもっとも書きたかったことです。この記事のためだけに、今まで (1)から(3)まで書いてきました。

第４回のテーマは

「循環小数 1/p の循環節の長さが
(p-1)/2 の約数となる条件」

です。これさえわかれば、循環小数の後半の桁がわかることは前回示しました。

その条件とはいったい何なのでしょうか。

先に言ってしまうと、それは次の条件です。

《定理４》
$1/p$ の循環節の長さが $(p-1)/2$ の約数となる必要十分条件は、
$p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ のいずれかであることである。

私が最初にこの条件を見たとき、

「なぜ 40 が関係があるのか」

と疑問に思いました。みなさんもそうでしょう。

でも安心してください。ちゃんと計算によって 40 という数字が出てくるのです。

しかもその計算には、初等整数論で最も美しいとされる定理

「平方剰余の相互法則」

が登場します。

期待に胸を膨らませて、《定理４》の証明に進んでいきましょう。

平方剰余との関係

第１回の記事では、次の条件が得られました。

《循環小数が $(p-1)$ 桁で循環する条件》

$\displaystyle 10^{(p-1)}\equiv 1 \pmod p$

これとまったく同様に、《循環節の長さが $(p-1)/2$ の約数となる条件》を考えると、次のようになるでしょう。

《循環節の長さが $(p-1)/2$ の約数となる条件》

$\displaystyle 10^{(p-1)/2}\equiv 1 \pmod p$

この左辺に着目します。
すると次の式とよく似ていることがわかります。

《オイラーの基準》

$\displaystyle \left(\frac{a}{p}\right)\equiv a^{(p-1)/2} \pmod p$
ただし、 $\displaystyle \left(\frac{a}{p}\right)$ は平方剰余を表すルジャンドル記号。

$a$ を $10$ で置き換えれば、まったく同一ですね。

したがって、《循環節の長さが $(p-1)/2$ の約数となる条件》は、平方剰余を使って次のように置き換えることができます。

《循環節の長さが $(p-1)/2$ の約数となる条件（の書き換え）》
$1/p$ の循環節の長さが $(p-1)/2$ の約数となる必要十分条件は

$\displaystyle \left(\frac{10}{p}\right) = 1$

が成り立つことである。

これで最初の問題が「平方剰余」と見事結びつきました！

あとはこの左辺を計算し、平方剰余になる $p$ の条件を考えればいいわけです。

ここで 《平方剰余の相互法則》 の登場です！

平方剰余の相互法則

証明はしませんが、今回使う 《平方剰余の相互法則》 をまとめます。

まずは、《平方剰余の定義》から。

《平方剰余の定義》
$a$ , $p$ を互いに素な整数とするとき、

$\displaystyle x^2\equiv a \pmod p$

が解をもつならば「 $a$ は $\pmod p$ で平方剰余である」という。
解を持たないならば、「 $a$ は $\pmod p$ で平方非剰余である」という。

このことをルジャンドル記号を用いて次のように表す。

$a$ は $\pmod p$ で平方剰余である

$\displaystyle \left(\frac{a}{p}\right)=1$

$a$ は $\pmod p$ で平方非剰余である

$\displaystyle \left(\frac{a}{p}\right)=-1$

続いて今回のメインディッシュである 《平方剰余の相互法則》 です。

《平方剰余の相互法則》
$p$ , $q$ を相異なる奇素数とするとき
$\displaystyle \left(\frac{p}{q}\right)\left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2}\cdot \frac{q-1}{2}}$

今回は使わないですが、重要な定理である 《第１補充則》 です。

《第１補充則》
$p$ を奇素数とするとき
$\displaystyle \left(\frac{-1}{p}\right) = (-1)^{\frac{p-1}{2}}$

《第２補充則》 は後程つかいます。

《第２補充則》
$p$ を奇素数とするとき
$\displaystyle \left(\frac{2}{p}\right) = (-1)^{\frac{p^2-1}{8}}$

最後に 《平方剰余の積に関する法則》 です。

《平方剰余の積に関する法則》
$p$ を奇素数、 $a$ , $b$ を互いに素な整数とするとき
$\displaystyle \left(\frac{ab}{p}\right) = \left(\frac{a}{p}\right) \left(\frac{b}{p}\right)$

これだけあれば十分でしょう。

フル活用して計算していきます。

《平方剰余の相互法則》を使って展開

それでは、 $\displaystyle \left(\frac{10}{p}\right)$ を展開していきましょう。

《平方剰余の積に関する法則》から、次式が得られます。

$\displaystyle \left(\frac{10}{p}\right) = \left(\frac{2}{p}\right)\left(\frac{5}{p}\right)$

左辺が平方剰余となる条件は、右辺が平方剰余の積となっていることから、

$\displaystyle \left(\frac{2}{p}\right)=1\;$ かつ $\displaystyle \;\left(\frac{5}{p}\right)=1$
または
$\displaystyle \left(\frac{2}{p}\right)=-1\;$ かつ $\displaystyle \;\left(\frac{5}{p}\right)=-1$

であることがわかります。

《第２補充則》より

$\displaystyle \left(\frac{2}{p}\right)=(-1)^{(p^2-1)/8}$

から $\displaystyle \left(\frac{2}{p}\right)$ が平方剰余となる必要十分条件は、 $p\equiv 1, 7 \pmod 8$ であることがわかります。逆に、非剰余となる条件は、 $p\equiv 3, 5 \pmod 8$ です。

また $\displaystyle \left(\frac{5}{p}\right)$ については、《平方剰余の相互法則》より、

$\displaystyle \left(\frac{5}{p}\right)\left(\frac{p}{5}\right) = (-1)^{\frac{5-1}{2}\cdot \frac{p-1}{2}} = 1$

から、

$\displaystyle \left(\frac{5}{p}\right) = \left(\frac{p}{5}\right)$

が得られることを利用します。
この右辺が 1 になることは、定義に戻って考えると、

$\displaystyle x^2\equiv p \pmod 5$

となるような $x$ が存在することと同値です。

$\pmod 5$ ですべてのパターンをチェックすると、

$1^2\equiv 1 \pmod 5$
$2^2\equiv 4 \pmod 5$
$3^2\equiv 4 \pmod 5$
$4^2\equiv 1 \pmod 5$

より、平方剰余となる条件は $p\equiv 1, 4 \pmod 5$ であることがわかります。逆に非剰余になる条件は $p\equiv 2, 3 \pmod 5$ です。

したがって、以上より次の関係がいえます。

$\displaystyle \left(\frac{10}{p}\right)=1$ であることの必要十分条件は、

$p\equiv 1, 7 \pmod 8\;$ かつ $\;p\equiv 1, 4 \pmod 5$
または
$p\equiv 3, 5 \pmod 8\;$ かつ $\;p\equiv 2, 3 \pmod 5$

あとは、連立合同式を解いていけばいいわけですが、もう数が多くないので $\pmod {40}$ で全列挙して考えましょう。

f:id:tsujimotter:20140404214421p:plain:w500

図の赤い四角が平方剰余、紫が平方非剰余をあらわしています。

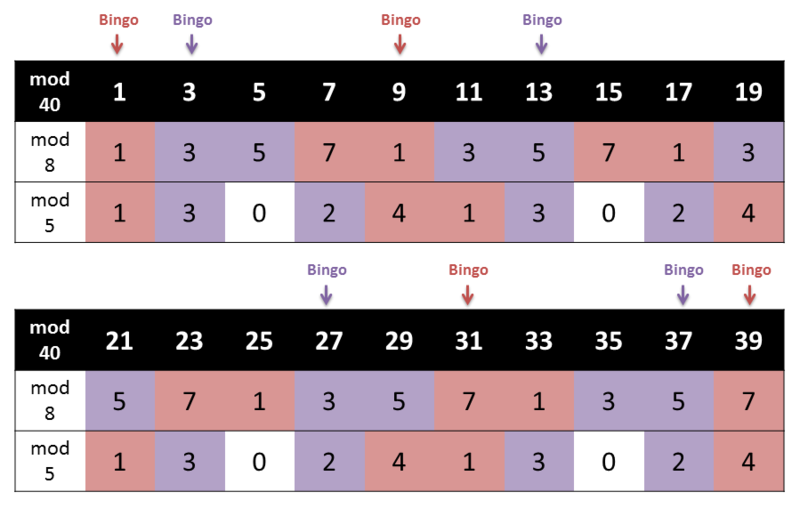
たしかに、1, 3, 9, 13, 27, 31, 37, 39 のときだけ、平方剰余・非剰余が一致していることがわかります。

これでついに、念願の条件が得られました。

$\displaystyle \left(\frac{10}{p}\right)=1$ であることの必要十分条件は、
$p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ のいずれかであることである。

翻って、元の命題に戻ると、

《定理４（再掲）》
$1/p$ の循環節の長さが $(p-1)/2$ の約数となる必要十分条件は、
$p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ のいずれかであることである。

が証明されたことになります。

1/12377 の 6193 桁目を計算しよう

ここで、最初の問題に立ち戻って考えてみましょう。

問題は

「 $1/12377$ の小数点以下 $6193$ 桁目の数」がどうなるか

ということでした。

$12377$ を $40$ で割った余りを考えて、

$12377 \equiv 17 \pmod {40}$

より、

$\displaystyle \left(\frac{10}{p}\right)=1$ であることの必要十分条件は、
$p$ を $40$ で割った余りが $1, 3, 9, 13, 27, 31, 37, 39$ のいずれかであることである。

から、

$\displaystyle \left(\frac{10}{12377}\right) = -1$

すなわち平方非剰余です。
したがって、 $1/12377$ の循環節の長さは、 $(12377-1)/2$ の約数になりません。

ここで、

《定理３（第３回の記事より）》
$1/p$ の循環節の長さを $e$ 、小数点以下 $\displaystyle k \left(\leq \frac{e}{2}\right)$ 桁目を $a_k$ とすると、

（中略）
2. $e$ が $(p-1)/2$ の約数でないとき

$a_{(p-1)/2+k} = 9 - a_k$