2017の素因数分解がつくる多角形

この記事は日曜数学 Advent Calendar 2016 の 25 日目（最終日）の記事です。

アドベントカレンダー最終日です！日曜数学アドベントカレンダーに参加してくださったみなさま，本当にありがとうございました。

さまざまな分野の楽しいお話が飛び出して，ワクワクしながら毎日を過ごすことができました。どれも気合いの入った魅力的な記事ばかりですので，まだご覧になっていない方は読んでみてください。
www.adventar.org

最終日なので「素晴らしい記事を振り返って終わり」としてもよかったのですが，どうしてもお話したいホットなお話ができてしまったので，語らせてください。

語りたいことが多すぎて，いつも通り長い記事になってしまいましたが，よかったらお付き合いください。

今日のテーマは素因数分解

この記事のタイトルを見て「2017 を "素因数分解" だって？」「素数なんだからこれ以上素因数分解できるわけがないじゃないか」
と思ったかもしれません。実はそんなに突飛なことではありません。

たとえば， $i = \sqrt{-1}$ をつかえば， $2017$ は

$2017 = (9 + 44i)(9 - 44i) \tag{1}$

の形に変形できますね。

高校で習う因数分解の公式を思い出してみてください。

$x^2 - y^2 = (x + y)(x - y)$

この式に $x = 9, \; y = 44i$ を代入すれば，上の式に一致しますね。

余談になりますが，私ははじめてこの話を知ったとき，授業で機械的に覚えさせられた「公式」が数論において重要な役割を担うことを理解して，ものすごく感動したことを覚えています。あぁ，あの公式はただ意味もなく覚えさせられたわけではなかったのか。

さて， $(9 + 44i), \; (9 - 44i)$ のような数を "素因数" とみなせるくらい頭を柔軟に考えれば，式 $(1)$ によって「2017 が "素因数分解" できた」といっても差し支えないでしょう。

少し技術的な話になりますが，実際，この "素因数とみなす" という考え方は，代数的整数論において正当化されます。 $(9 + 44i), \; (9 - 44i)$ という数は，有理数体 $\mathbb{Q}$ に $i$ を添加した拡大体 $\mathbb{Q}(i)$ の整数環 $\mathbb{Z}[i]$ における「素元」となります。

本日は拡大した世界における素因数分解の法則とそれに伴って導かれる多角形についてのお話です。素因数分解のようすが図形の形となって現れるという面白さをぜひ体感していただきたいです。

素因数分解の法則

非常に面白いことに，こんな風に $i$ を加えて "素因数分解" ができる素数は

4 で割って 1 あまる素数

に限ります。（たとえば 7 とか 11 を分解してみてください。どうやっても分解できないことがわかります。）

しかも，このような 4 で割って 1 あまる素数はすべて "素因数分解" できるのです！

これだけでも十分すごいのですが，さらに面白い話があります。この "素因数分解" は図形的に解釈可能なのです。

上記のように "素因数分解" できる素数は，すべて

「整数を辺にもつ直角三角形の斜辺」

になります。2017 は 4 で割って 1 あまる素数なので，上記のような法則が当てはまるとても都合のよい数なのです。

実際，以下のような直角三角形が得られます。

f:id:tsujimotter:20161225195740p:plain:w400

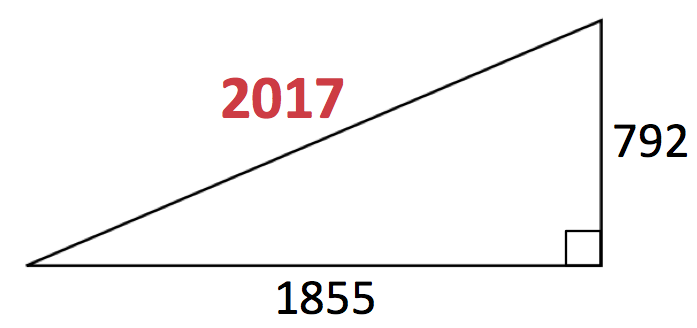
実はこの話にはさらに続きがあって，一般に m で割って 1 あまる素数は，すべてこのような面白い法則を作ることができ，それに伴って整数の辺を持つ多角形と関連します。

2017 は大変喜ばしいことに

2017 = 2016（約数がとても多い数） + 1

の形をした素数であるので，このような法則の宝庫といえるでしょう。

たとえば，2017 は 3で割って 1 あまる素数なのですが，このような素数は「整数辺を持ち鈍角が 120° である三角形の斜辺」となります。

f:id:tsujimotter:20161225195804p:plain:w400

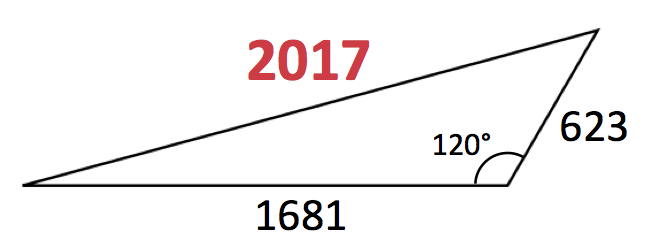
このあたりの話は「数論への招待」という本にも載っているので見たことある方は多いでしょう。

数論への招待 (シュプリンガー数学クラブ)

作者:加藤和也
発売日: 2012/11/27
メディア: 単行本（ソフトカバー）

「数論への招待」では５角形の例も登場しますが，今回扱う $2017$ は残念ながら $5$ で割って $1$ あまる素数ではありません。残念。

$5$ で割って $1$ あまる素数である $2081$ 年まで待ちましょう。この記事を読んだ誰がその年に立ち会えるというのだろう。

素因数分解から作る７角形

さてここからが本題です。

7 で割って 1 あまる素数でもある 2017 は，

（とある条件を満たす）整数の辺だけを持つ７角形の一辺

にもなります。なんだその条件はと思うかもしれませんが，まぁ聞いてください。

この法則は「 $m$ で割ったあまりが $1$ である素数は， $m$ 分体で完全分解する」という，円分体の類体論により自然に導かれるものです。

ところが，この法則を用いてつくられた７角形の具体例を見たことがありませんでした。きっと上にあげた「4 で割って 1 あまる素数」や「3 で割って 1 あまる素数」の法則と比べて，問題が複雑すぎるのが原因でしょう。しかし，数を愛する者としては，4 や 3 だけを特別扱いしたくありません。

というわけで，おそらく誰も見たことがないであろう「2017 の素因数分解がつくる７角形」の作図に挑戦してみたいと思います。

まず， $2017$ は $7$ で割って $1$ あまる素数なので，円分体の類体論より $\zeta_7$ （１の原始７乗根）を使って以下のように "素因数分解" できます。

$\begin{eqnarray} 2017 = &&(3\zeta_7 + 3\zeta_7^3 + 2\zeta_7^4 + \zeta_7^5) \\ &&\times (- 3\zeta_7 - \zeta_7^2 - 3\zeta_7^3 - 3\zeta_7^4 -2\zeta_7^5) \\ && \times (1 + \zeta_7 - 2\zeta_7^2 + \zeta_7^3 - \zeta_7^4 -2\zeta_7^5) \\ && \times (2\zeta_7 + 3\zeta_7^3 + 3\zeta_7^4 + \zeta_7^5) \\ && \times (1 - 2\zeta_7 + \zeta_7^2 - 2\zeta_7^3 - 2\zeta_7^4 -\zeta_7^5 ) \\ && \times (\zeta_7 + 3\zeta_7^2 + 2\zeta_7^3 + 3\zeta_7^5) \end{eqnarray} \tag{2}$

以下では，この素因数分解の法則から，2017 を一辺に持つ整数辺７角形を作る方法を解説します。

まず，上の素因数の中から３つ選んでそれを $A$ とします。ここでは，１番目と４番目と６番目を選んで

$\begin{eqnarray} A = && (3\zeta_7 + 3\zeta_7^3 + 2\zeta_7^4 + \zeta_7^5) \\ && \times (2\zeta_7 + 3\zeta_7^3 + 3\zeta_7^4 + \zeta_7^5) \\ && \times (\zeta_7 + 3\zeta_7^2 + 2\zeta_7^3 + 3\zeta_7^5) \end{eqnarray}$

とし，残りの３つを掛け合わせて

$\begin{eqnarray} \overline{A} = && (- 3\zeta_7 - \zeta_7^2 - 3\zeta_7^3 - 3\zeta_7^4 -2\zeta_7^5) \\ && \times (1 + \zeta_7 - 2\zeta_7^2 + \zeta_7^3 - \zeta_7^4 -2\zeta_7^5) \\ && \times (1 - 2\zeta_7 + \zeta_7^2 - 2\zeta_7^3 - 2\zeta_7^4 -\zeta_7^5 ) \end{eqnarray}$

としましょう。

もし，うまい３つを選ぶことができれば， $A$ と $\overline{A}$ は複素共役になります。実際，上の $A$ と $\overline{A}$ は複素共役になっています。

当然，

$2017 = A \overline{A}$

となっているわけですが， $A$ と $\overline{A}$ が複素共役であれば，

$2017 = |A^2|$

が成り立ちますね。

ここで１つ「おまじない」をします。

$|\zeta_7| = 1$ より，

$2017 = \left|(\zeta_7^{6} A)^2\right|$

も成り立ちます。そこで，以後 $A$ に $\zeta_7^6$ をかけたものを考えます（理由は後述）。

この $(\zeta_7^6 A)^2$ を展開すると，

$(\zeta_7^6 A)^2 = 2196 + 1065\zeta_7 + 1740\zeta_7^2 + 1664\zeta_7^3 + 1716\zeta_7^4 + 636\zeta_7^5$

が成り立ちます。これで目的の式が得られました。

絶対値をとると，

$2017 = \left|2196 + 1065\zeta_7 + 1740\zeta_7^2 + 1664\zeta_7^3 + 1716\zeta_7^4 + 636\zeta_7^5\right| \tag{3}$

が成り立ちます。

「この式が一体なんなんだ？」

という声が聞こえてきそうですが，これでもう完成なのです。式 $(3)$ を図形的に解釈すると，そのまま目的の７角形が出来上がるのです。

図を使って説明してみましょう。

まず，複素数平面上に $2196$ という点を描画します。すると， $0$ と $2196$ を結ぶ線分が得られます（下図 (1) を参照）。

次に， $2196$ に $1065\zeta_7$ を加えた点 $2196+1065\zeta_7$ を描画します。これは，長さ $1065$ の線分を，実軸に対して $\theta = 2\pi/7$ だけ回転させてできる線分を， $2196$ に繋げることで得られます（下図 (2) を参照）。

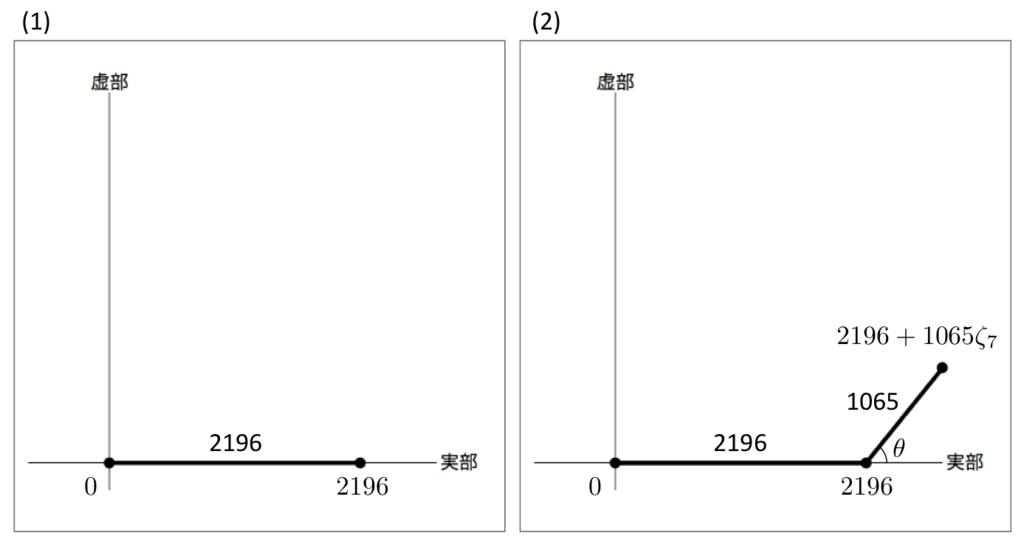
さらに， $1740\zeta_7^2$ を加えた点を描画したいのですが，これは長さ $1740$ の線分を $\theta$ 回転させて，さらに $\theta$ 回転させたものを点 $2196+1065\zeta_7$ につなげて得られます。

これを続けていくと，以下のような７つの点列をつなぐパスができます。

f:id:tsujimotter:20161225172223p:plain:w600

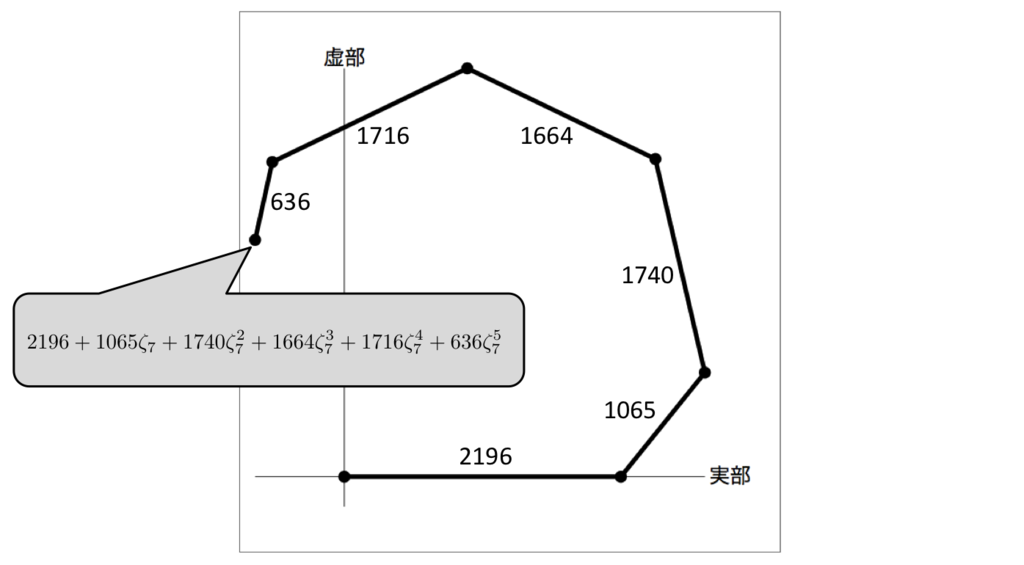
パスを構成するすべての線分の長さはすべて整数で，またすべての線分同士のなす角が等しいことに注意してください。

さらに，パスの終端の点 $2196 + 1065\zeta_7 + 1740\zeta_7^2 + 1664\zeta_7^3 + 1716\zeta_7^4 + 636\zeta_7^5$ の原点からの長さは $2017$ に一致します（これは式 $(3)$ から明らかですね！）。

結論として，始点（原点）と終点を結ぶことで，以下の多角形ができあがります！

f:id:tsujimotter:20161225172309p:plain:w480

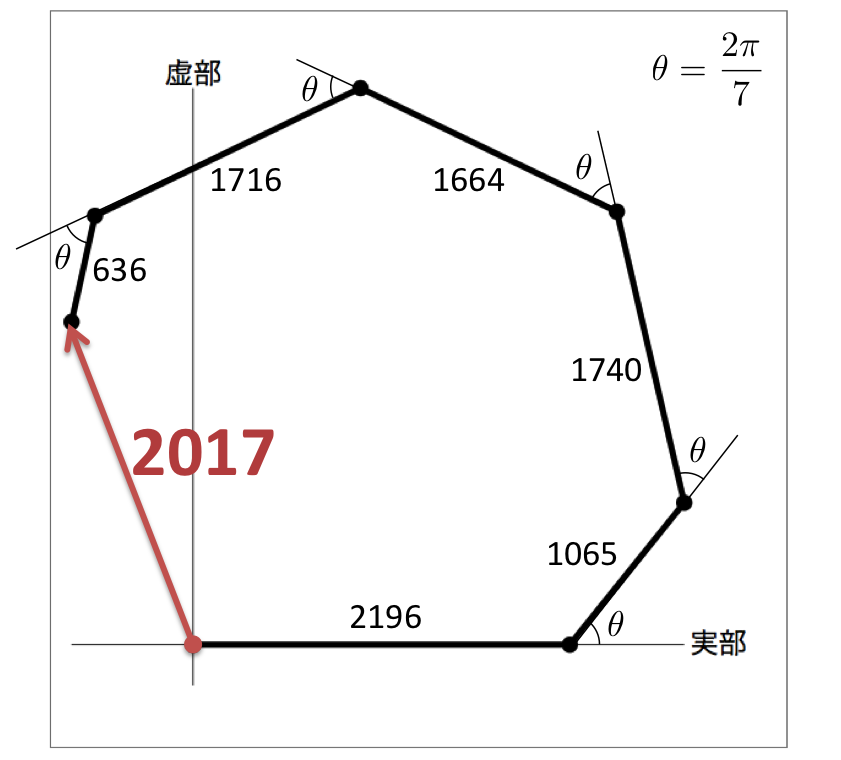
これこそ， $2017$ の素因数分解の法則から自然に導かれた７角形です。どこの本にも載っていない，筆者オリジナルの作品ですので，おそらく誰もまだ見たことのない多角形でしょう。

せっかくなので，線だけのバージョンも掲載しましょう。

http://tsujimotter.info/works/2017/2017-heptagon.svg

上の画像は SVG というベクターデータの形式なので，いろいろな用途にお使いできます。よろしければ，2017年の年賀状などにお使いください。

ほんとに作りました。笑

2017年の年賀状できた！今度の #日曜数学会で配ります^_^ pic.twitter.com/rvLJM2e0Dv
— tsujimotter (@tsujimotter) 2017年1月5日

作り方（７角形を作るための長い道のり）

７角形もできたし「めでたしめでたし」と2017年を締めくくりたいところなのですが，やっぱり作り方も知りたいですよね。以下ではその作り方を具体的にご説明しましょう。

以下，技術的な説明と tsujimotter の試行錯誤の過程が続きます。
必要に応じて読み飛ばしてください。

７角形を作る方法ですが，考え方がシンプルな割りに，実際に作るのは少し難しいです。問題はいくつかの小問題に区分けできます。

2017 を素因数分解する方法

まず第一に「どうやって 2017 を素因数分解するのか」という問題があります。

少し技術的な説明をします。

一般論として， $f(X)$ を $\alpha$ の $\mathbb{Q}$ 上の最小多項式とし， $K$ の整数環 $\mathfrak{O}_K$ が $\mathfrak{O}_K = \mathbb{Z}[\alpha]$ となるとき， $\mathbb{Q}(\alpha)$ 上の $p$ の素イデアル分解は以下のように得られます。

$f(X) \equiv \varphi_1(X)^{e_1}\varphi_2(X)^{e_2}\cdots \varphi_g(X)^{e_g} \pmod{p}$

という表示で与えられる $f(X)$ の $\bmod{p}$ で既約な多項式による分解を $\varphi_i(X)$ としたとき， $p$ は

$\mathfrak{P}_i = (p, \varphi_i(\alpha))$

によって次のように素イデアル分解されます。

$p = \mathfrak{P}_1^{e_1} \mathfrak{P}_2^{e_2} \cdots \mathfrak{P}_g^{e_g}$

ところが，この素イデアル $\mathfrak{P}_i$ は単項イデアルの形でかけていませんので，そのまま素因数分解の形に持っていくことができません。

以上の操作は面倒だと考えましたので，おとなしく数式処理ソフトを用いることにしました。使ったのは，SageMathというソフトウェアです。

SageMath は数学の幅広い処理を扱う数式処理ソフトウェアで，今回の目的である「代数的整数論」に関する処理を実行するツールがたくさん用意されています。しかも，素晴らしいことにソフトウェアをインストールすることなく，ウェブ上で実行することができるのです。

SageMathCloudというサービスがあります。以下のリンクからアクセスできます。

SageMath - Open-Source Mathematical Software System

アカウントを登録する必要はありますが，基本的に無料で利用できます。以下の動画に SageMathCloud を用いて計算をはじめる手順を簡単にまとめましたので，興味のある方はご覧になってください。

youtu.be

さて，以下では SagaMath のコマンドを使って解説していきます。

まず，有理数体 $\mathbb{Q}$ に $\zeta_7$ を加えた世界，代数体（number field）を作ります。変数は $K$ としておきましょう。

K.<z> = NumberField(x^6 + x^5 + x^4 + x^3 + x^2 + x + 1); K

このコマンドを打って，Shift を押しながら Enter キーをたたきましょう。すると，

Number Field in z with defining polynomial x^6 + x^5 + x^4 + x^3 + x^2 + x + 1

のようなメッセージが返ってきます。これで代数体 $K$ ができました。

$\zeta_7$ の最小多項式は $f(X) = x^6 + x^5 + x^4 + x^3 + x^2 + x^1 + 1$ なので，この式を NumberField という関数の引数に指定しています。このような式を定義多項式（defining polynominal）といいますね。

z というのは， $\zeta_7$ のことを表す変数です。代数体を定義する際に，以下のように「定義多項式の根」を明示的に指定することができます。

K.<z>

この z が $\zeta_7$ を表すことを確認するために，以下のコマンドを打って実行（Shift + Enter）してみましょう。

z^7

すると， $1$ というメッセージが返ってくるはずです。 $z^7 = 1$ が確認できました。

次に， $2017$ を $K$ 上で "素因数分解" しましょう。

少し技術的な注意をすると， $K = \mathbb{Q}(\zeta_7)$ の整数環は単項イデアル整域なので，一意に素因数分解できるのですが，このソフトでは標準的に「素イデアル分解」されます。したがって，分解されて得られるのは分数イデアル（fractional ideal）です。

I = K.ideal(2017)
I.factor()

(Fractional ideal (z^5 + 2*z^4 + 3*z^3 + 3*z)) * (Fractional ideal (-2*z^5 - 3*z^4 - 3*z^3 - z^2 - 3*z)) * (Fractional ideal (-2*z^5 - z^4 + z^3 - 2*z^2 + z + 1)) * (Fractional ideal (z^5 + 3*z^4 + 3*z^3 + 2*z)) * (Fractional ideal (-z^5 - 2*z^4 - 2*z^3 + z^2 - 2*z + 1)) * (Fractional ideal (3*z^5 + 2*z^3 + 3*z^2 + z))

結果から，以下の６つの分数イデアルに分解されたことがわかるでしょう。

(z^5 + 2*z^4 + 3*z^3 + 3*z)
(-2*z^5 - 3*z^4 - 3*z^3 - z^2 - 3*z)
(-2*z^5 - z^4 + z^3 - 2*z^2 + z + 1)
(z^5 + 3*z^4 + 3*z^3 + 2*z)
(-z^5 - 2*z^4 - 2*z^3 + z^2 - 2*z + 1)
(3*z^5 + 2*z^3 + 3*z^2 + z)

これらのイデアルの生成元はすべて整係数となっているので，整イデアルですね。しかも単項イデアルで表されているので，これらの生成元をそのまま掛け合わせれば，2017 の単数倍の数ができあがります。

実際，

(z^5 + 2*z^4 + 3*z^3 + 3*z)*(-2*z^5 - 3*z^4 - 3*z^3 - z^2 - 3*z)*(-2*z^5 - z^4 + z^3 - 2*z^2 + z + 1)*(z^5 + 3*z^4 + 3*z^3 + 2*z)*(-z^5 - 2*z^4 - 2*z^3 + z^2 - 2*z + 1)*(3*z^5 + 2*z^3 + 3*z^2 + z)

のコマンドを実行すると，

2017*z^5 + 2017*z^4 + 2017*z^3 + 2017*z^2 + 2017*z + 2017

すなわち，

（６つの素因数の積） $= 2017(1+\zeta_7+\zeta_7^2+\zeta_7^3+\zeta_7^4+\zeta_7^5)$

となります。この，

$1+\zeta_7+\zeta_7^2+\zeta_7^3+\zeta_7^4+\zeta_7^5$

の部分が単数になっていて，実際

$1+\zeta_7+\zeta_7^2+\zeta_7^3+\zeta_7^4+\zeta_7^5 = -\zeta_7^6$

が成り立ちます（最初からこう書いてくれたらいいのに・・・）。

$_6C_3$ の組み合わせ

さて，得られた６つの素因数の中から３つを選んで，積がその残りの積と共役になるようにしたいですね。ここで，どの３つを選ぶのかという新たな問題が現れます。

私はこのためのうまい方法を知りません。適当に選ぶしかありませんでした。選んだ３つの素因数の積を $A$ として，その $A$ を自乗して絶対値をとります。うまくいけば $2017$ に一致します。

何回かの試行錯誤の上，「当たり」を引くことができました。

A = (z^5 + 2*z^4 + 3*z^3 + 3*z) * (z^5 + 3*z^4 + 3*z^3 + 2*z) * (3*z^5 + 2*z^3 + 3*z^2 + z); A
(A^2).abs()

結果は以下です。

-11*z^5 + 4*z^4 + 20*z^3 + 34*z^2 - 10*z + 20
2017.00000000000

たしかに， $A^2$ の絶対値が $2017$ に一致しますね。

あとは， $A^2$ を展開してあげればよいです。

A^2

-52*z^5 + 24*z^4 - 651*z^3 + 480*z^2 - 1716*z - 1080

やったー。これで，目的の式が得られました。

$2017 = \left|-1080 - 1716\zeta_7 + 480\zeta_7^2 - 651\zeta_7^3 + 24\zeta_7^4 - 52\zeta_7^5\right|$

これを前節で解説した方法でそのまま図示してあげましょう。

f:id:tsujimotter:20161225190800p:plain:w400

あれ？

何かがおかしい

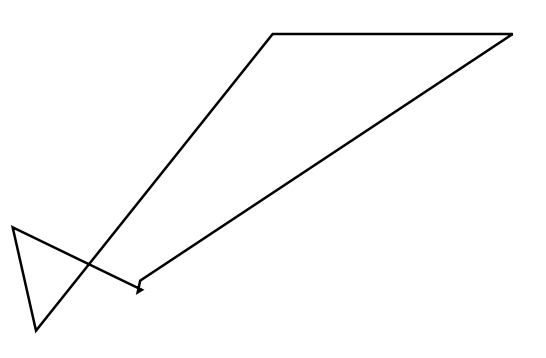
数値をつけて分析してみましょう。

f:id:tsujimotter:20161225190709p:plain:w400

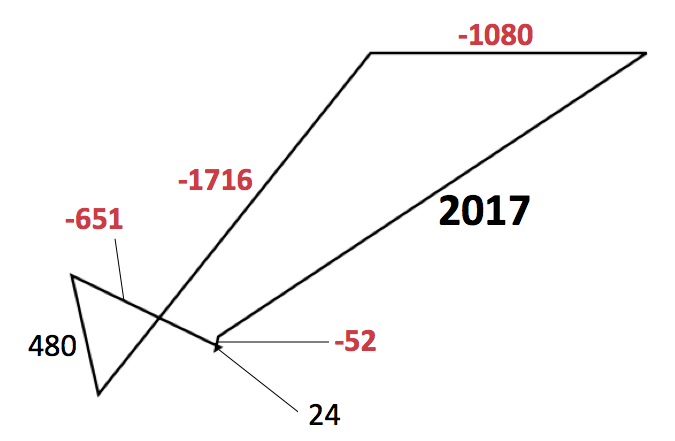
なるほど。係数にマイナスがついてしまうと，線分の伸びる方向が想定した方向と反対になってしまうのですね。つまり，凸多角形にならない。

というわけで，今回できた完成品の７角形はこちらです。

〜完〜

としたいところですが，こんな７角形じゃ愛着持てないですよね。

凸多角形にするために

もう少し美しくしたい。具体的には，得られる多角形を凸多角形に限定したい。

正直なところ，tsujimotter は上の図形が現れた段階で意気消沈していました。まさか，こんな展開があるなんて。きれいな７角形は作れないのかと。

諦めかけていた tsujimotter に神様（加藤先生）が語りかけます。ここで諦めてはいけないと。

そして，再び考え始めた tsujimotter にひらめきが訪れます。

そうだ，単数倍すればいいんだ！

単数って素晴らしいんですよ。イデアルに単数をどんなにかけてもイデアルは同じままです。今回の目的では，絶対値が 2017 に一致すればよいわけですから， $A$ に絶対値が $1$ である単数をかけても問題ないのです。 $1$ のべき乗根は，ちょうどそんな単数になっています。

前節の「おまじない」と言っていた部分はこのことだったのですね。伏線回収。

というわけで， $A$ に１のべき乗根 $\zeta_7^k$ をかけまくって， $(\zeta_7^k A)^2$ の係数がすべて正になるものを探しましょう！

A = (z^5 + 2*z^4 + 3*z^3 + 3*z) * (z^5 + 3*z^4 + 3*z^3 + 2*z) * (3*z^5 + 2*z^3 + 3*z^2 + z)

A^2
(z*A)^2
(z^2*A)^2
(z^3*A)^2
(z^4*A)^2
(z^5*A)^2
(z^6*A)^2

実行結果は以下のようになります。

-11*z^5 + 4*z^4 + 20*z^3 + 34*z^2 - 10*z + 20
-52*z^5 + 24*z^4 - 651*z^3 + 480*z^2 - 1716*z - 1080
-675*z^5 + 456*z^4 - 1740*z^3 - 1104*z^2 - 24*z - 76
-2196*z^5 - 1560*z^4 - 480*z^3 - 532*z^2 - 456*z - 1131
1080*z^5 + 1028*z^4 + 1104*z^3 + 429*z^2 + 1560*z - 636
76*z^5 - 599*z^4 + 532*z^3 - 1664*z^2 - 1028*z + 52
1131*z^5 - 1065*z^4 - 429*z^3 + 651*z^2 + 599*z + 675
636*z^5 + 1716*z^4 + 1664*z^3 + 1740*z^2 + 1065*z + 2196

最後の一行をみてください。

636*z^5 + 1716*z^4 + 1664*z^3 + 1740*z^2 + 1065*z + 2196

これこそ求めていた「すべての係数が正となる式」ですね。絶対値をとると

$2017 = \left|2196 + 1065\zeta_7 + 1740\zeta_7^2 + 1664\zeta_7^3 + 1716\zeta_7^4 + 636\zeta_7^5\right| \tag{3}$

が無事得られました。

これを図示すれば，求めていた愛すべき凸７角形が得られるわけです。

最後に７角形を鑑賞して解説を終わりにしましょう。

いやぁ，これまでの過程を踏まえると，この７角形が愛らしく見えてきますね。生まれてきてくれてありがとう。

まとめ

きょうは「2017の素因数分解の法則」から導かれる「整数を辺に持つ多角形」についてのお話しでした。

結果として得られる図形をみるだけでも楽しいですが，それを導く過程もなかなか面白いですよね。背景を理解すればするほど，素因数分解の法則が不思議に感じますし，そこから得られた図形に愛着が生まれるものです。また（素因数分解のような）整数や代数の法則が図形として解釈できるという発想は非常に面白いと思っていて，この考え方はほかにもさまざまな応用がありそうですよね。

今回の作品は，以前，サイエンスアゴラ2016というイベントでも紹介していました。
tsujimotter.hatenablog.com

このときは「２５個の作品を短時間で紹介する」というプレゼンだったので，図形を表示した時間はほんの一瞬で，導く過程はほとんど紹介できませんでした。いつかじっくり解説したいと思っていたのですが，アドベントカレンダーをきっかけにまとめることができました。

苦労話を入れすぎて，随分長い記事になってしまいました。最後まで読んでくださった皆様ありがとうございました。

今回紹介した SageMath は非常に便利なツールなので，これを機会にぜひ使ってみてくださいね！

ではでは，2016 年もありがとうございました！

2017 は，今回紹介したほかにもたくさん面白い性質を持った数ですので，とても楽しい一年になりそうですね！

2017 年も楽しく日曜数学しましょう！それでは！*1

「 $4$ で割って $1$ あまる素数は， $i$ を加えた世界で分解する」の解説記事です。
tsujimotter.hatenablog.com