2017は非正則素数 - tsujimotterのノートブック

今年は西暦 2017 年ですが，2017 は素数ということで各所で盛り上がったことと思います。

実は，2017は単に素数なだけではなく，非正則素数という重要な素数でもあるのです。今日はそのことを紹介します。

概要：

さっき発見したんですが 2017 は 123 番目の非正則素数なんですね！めでたい。調べてみると 2017 は ζ(-1203) の分子を割り切るので、こんな関係が成り立ちますね（A_Q(μ_2017) は円の 2017 分体のイデアル類群のp-部分、ωはタイヒミュラー指標）。 pic.twitter.com/wsQNpenQav
— tsujimotter ロマ数本好評発売中!! (@tsujimotter) 2017年1月5日

非正則素数ってなんだっけ？

非正則素数について簡単に復習しましょう。

素数を $p$ として， $p$ 次の円分体（円の $p$ 等分点を有理数体 $\mathbb{Q}$ に添加した体）を $\mathbb{Q}(\mu_p)$ と表し，そのイデアル類群を

$\mathrm{Cl}_{\mathbb{Q}(\mu_p)}$

とします。そのイデアル類群の位数，つまり類数を割り切る素数のことを非正則素数といいます。逆に，割り切らない素数は正則素数と呼ばれます。

非正則素数が数学史に登場したのは，フェルマーの最終定理のクンマーによる部分的解法からと言われています。類数を割り切らない素数，正則素数についてのフェルマーの最終定理は，イデアル類群の構造を巧妙につかって解決できるのです。これについては，以下の記事で詳しくまとめています。
tsujimotter.hatenablog.com

たとえば，フェルマーの最終定理に関するクンマーの方法では，正則素数に限り「整数解が存在しないこと」を示すことができますが，

$X^{2017}+Y^{2017} = Z^{2017}$

については，クンマーの方法では示すことができません。

「フェルマーの最終定理を解決できない素数」というとネガティブなイメージですが，実は非正則素数には１つ面白い話があります。非正則素数はリーマン・ゼータの値と関係があるのです。これは驚くべきことです。

ゼータ関数の負の奇数値 $\zeta(1-r)$ （ $r$ は偶数）を既約分数で表したときの分子に現れる素数は，なんと非正則素数だけなのです。逆に言えば，ゼータの分子に現れる素数は非正則素数だけです。これもクンマーが発見したことです。

たとえば，有名なゼータの特殊値

$\displaystyle \zeta(-11) = \frac{691}{32760}$

は，分子に $691$ が現れていますが，この時点で $691$ が非正則素数であることがわかるのです。 $p=691$ のイデアル類群を計算するのは大変ですが，これなら一瞬で非正則素数であることが分かってしまいますね。

$2017$ は，（頑張って計算すると） $\zeta(-1203)$ の分子を割り切ることがわかるので，非正則素数であることがわかります。なお，ゼータの値はこうなります。

zeta(–1203) = 13020708964309151369900893536099359935580848290805387107021264423382611001331265031156199406189568933357437918927422171654926698371796570056223937089561175157549993019185909946293481739994875312093198331761669287037603763797673617047030997333811323082724975319096756847013918994438061132312345680919842503230191223525884025250698697306218109191481721823125045762602943830666574381377737528296853113560063733147255480312203915218317507337813955820583647820409144941416605184803275335786040337094236114626705668872995224802105955634174791463306876418723831371109306902102173189604126889199068093789021548036497146748854762705691516896543071578620443914335937532115243154553073763023368196139248342580828361147023217024411949350255138870101619434237528811354697380704917517435543096873581137687501846737837505763805282269533822720611622619472851678006669902311797007736508866208756146329624124022282604351098688213745176070015697390718340119890779594796968371129158815841689795123431582751034066516603253844221992524435839084024758597824518144901154499365428127881662096395405245455304006133588967166702243224275265641514771297657622851599875727678528544882871428408063748976608273848844921846346730554127618845146754077285074244496432327127762752960987373379418328380328825690410543601753610854418862040751691785248191461254702755570291142400241367425039220764728036914108019933989471502875488546383258308823866468762457377015581934332095431851444402941713827805840671465165644671432902822132769456134876276140932101243740537342194786186329125869694630201716057163734584612128904562728270688599900000197713584902808468757050059544797117593682235252969509967230681934972818824453084180935246985552490084543490938678841108079423880272748788127912957755862569432711632223878594737094435502024186499655382940968315531431122053818527333209673096279838885106732690033181655613243004565683251642702746013833348325425384178751340071950410403779433977528413970118104853214804516500532340201167425186775526581177844603802095284207803363515738624910385834037694841996854325884655062712248764925423448129222848013922077713925319104776408599583206837539986412617843730640731391379162491954240441228405921051730286516859245347467277193120668800917/602040

長い。笑

ゼータとイデアル類群という，一見まったく関係なさそうな２つの対象が密接に結び付くという，きわめて面白いことが起きているわけです。すごい。

もっとイデアル類群のことがわかる

実は $p$ 次の円分体のイデアル類群については，もう少し詳しく知ることができます。

上の定理で言っているのはイデアル類群が $p$ で割れるかどうかなので，私たちは $p$ に関する部分に関心があります。シローの定理というものがあって，群の位数が $p$ のべきを約数に持つとき， $p$ のべきの位数を持つ部分群を持つことがわかります。これを $p$ -部分といいます。さらに，イデアル類群を $p$ -部分とそうでない部分の直和に分解できることが知られています。

イデアル類群の $p$ -部分を $A_{\mathbb{Q}(\mu_p)}$ と書くことにしましょう。すると，非常に面白いことに，この $A_{\mathbb{Q}(\mu_p)}$ の構造と「 $p$ がどのゼータを割るか」が関係するのです。（先ほどのクンマーの定理は，どのゼータを割るかとは無関係だったことに注意）

具体的には，以下に示すエルブラン・リベの定理が成り立って，イデアル類群の $p$ -部分に対するガロア群の作用がよくわかるというのです。

$A^{\omega^{1-r}} \neq 0 \; \;\Longleftrightarrow \; \zeta(1-r)\equiv 0 \pmod{p}$

$\omega$ はタイヒミュラー指標です。左辺はイデアル類群を指標で捻った群が非自明であることを表し，右辺の合同式は「（左辺）－（右辺）の既約分数の分子が $p$ で割り切れること」を表します．

詳しい定義については私もあまり正確に説明できる自信がないので，たとえば以下の「数論２」とかを読んでいただければと思います。

数論〈2〉岩沢理論と保型形式

作者:信重, 黒川,毅, 斎藤,将人, 栗原
発売日: 2005/02/08
メディア: 単行本

これを踏まえると， $p = 2017$ は $\zeta(-1203)$ の分子を割り切るので，こんな関係が成り立つことになりますね（ $-1203$ も覚えたくなる！）。

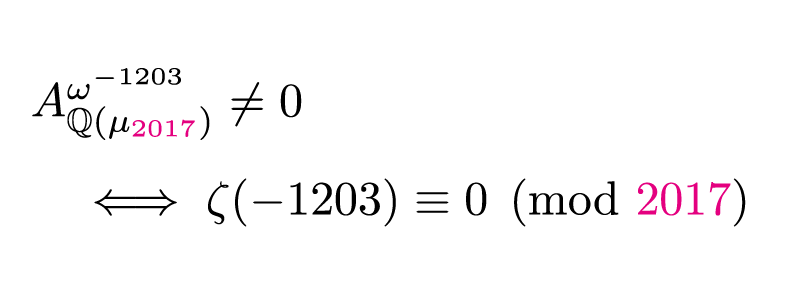
f:id:tsujimotter:20170106110020p:plain:w400

いやー，2017年めでたい。

2100以下の非正則素数とゼータの合同式

2100以下の非正則素数をまとめました。これだけ覚えておけば，とりいそぎ死ぬまで困らないですね。

37, 59, 67, 101, 103, 131, 149, 157, 233, 257, 263, 271, 283, 293, 307, 311, 347, 353, 379, 389, 401, 409, 421, 433, 461, 463, 467, 491, 523, 541, 547, 557, 577, 587, 593, 607, 613, 617, 619, 631, 647, 653, 659, 673, 677, 683, 691, 727, 751, 757, 761, 773, 797, 809, 811, 821, 827, 839, 877, 881, 887, 929, 953, 971, 1061, 1091, 1117, 1129, 1151, 1153, 1193, 1201, 1217, 1229, 1237, 1279, 1283, 1291, 1297, 1301, 1307, 1319, 1327, 1367, 1381, 1409, 1429, 1439, 1483, 1499, 1523, 1559, 1597, 1609, 1613, 1619, 1621, 1637, 1663, 1669, 1721, 1733, 1753, 1759, 1777, 1787, 1789, 1811, 1831, 1847, 1871, 1877, 1879, 1889, 1901, 1933, 1951, 1979, 1987, 1993, 1997, 2003, 2017, 2039, 2053, 2087, 2099

前回の非正則素数は 2003 年で，次の非正則素数は 2039 年ですね．22世紀までにあと残り 4 回しかないので大切に祝いましょう。

せっかくなので， $p$ が $\zeta(1-r)$ を割り切る合同式を眺めましょう。

$\zeta(-31) \equiv 0 \pmod{37}$

$\zeta(-43) \equiv 0 \pmod{59}$

$\zeta(-57) \equiv 0 \pmod{67}$

$\zeta(-67) \equiv 0 \pmod{101}$

$\zeta(-23) \equiv 0 \pmod{103}$

$\zeta(-21) \equiv 0 \pmod{131}$

$\zeta(-129) \equiv 0 \pmod{149}$

$\zeta(-61) \equiv \zeta(-109) \equiv 0 \pmod{157}$

$\zeta(-83) \equiv 0 \pmod{233}$

$\zeta(-163) \equiv 0 \pmod{257}$

$\zeta(-99) \equiv 0 \pmod{263}$

$\zeta(-83) \equiv 0 \pmod{271}$

$\zeta(-19) \equiv 0 \pmod{283}$

$\zeta(-155) \equiv 0 \pmod{293}$

$\zeta(-87) \equiv 0 \pmod{307}$

$\zeta(-291) \equiv 0 \pmod{311}$

$\zeta(-279) \equiv 0 \pmod{347}$

$\zeta(-185) \equiv \zeta(-299) \equiv 0 \pmod{353}$

$\zeta(-99) \equiv \zeta(-173) \equiv 0 \pmod{379}$

$\zeta(-199) \equiv 0 \pmod{389}$

$\zeta(-381) \equiv 0 \pmod{401}$

$\zeta(-125) \equiv 0 \pmod{409}$

$\zeta(-239) \equiv 0 \pmod{421}$

$\zeta(-365) \equiv 0 \pmod{433}$

$\zeta(-195) \equiv 0 \pmod{461}$

$\zeta(-129) \equiv 0 \pmod{463}$

$\zeta(-93) \equiv \zeta(-193) \equiv 0 \pmod{467}$

$\zeta(-291) \equiv \zeta(-335) \equiv \zeta(-337) \equiv 0 \pmod{491}$

$\zeta(-399) \equiv 0 \pmod{523}$

$\zeta(-85) \equiv 0 \pmod{541}$

$\zeta(-269) \equiv \zeta(-485) \equiv 0 \pmod{547}$

$\zeta(-221) \equiv 0 \pmod{557}$

$\zeta(-51) \equiv 0 \pmod{577}$

$\zeta(-89) \equiv \zeta(-91) \equiv 0 \pmod{587}$

$\zeta(-21) \equiv 0 \pmod{593}$

$\zeta(-591) \equiv 0 \pmod{607}$

$\zeta(-521) \equiv 0 \pmod{613}$

$\zeta(-19) \equiv \zeta(-173) \equiv \zeta(-337) \equiv 0 \pmod{617}$

$\zeta(-427) \equiv 0 \pmod{619}$

$\zeta(-79) \equiv \zeta(-225) \equiv 0 \pmod{631}$

$\zeta(-235) \equiv \zeta(-241) \equiv \zeta(-553) \equiv 0 \pmod{647}$

$\zeta(-47) \equiv 0 \pmod{653}$

$\zeta(-223) \equiv 0 \pmod{659}$

$\zeta(-407) \equiv \zeta(-501) \equiv 0 \pmod{673}$

$\zeta(-627) \equiv 0 \pmod{677}$

$\zeta(-31) \equiv 0 \pmod{683}$

$\zeta(-11) \equiv \zeta(-199) \equiv 0 \pmod{691}$

$\zeta(-377) \equiv 0 \pmod{727}$

$\zeta(-289) \equiv 0 \pmod{751}$

$\zeta(-513) \equiv 0 \pmod{757}$

$\zeta(-259) \equiv 0 \pmod{761}$

$\zeta(-731) \equiv 0 \pmod{773}$

$\zeta(-219) \equiv 0 \pmod{797}$

$\zeta(-329) \equiv \zeta(-627) \equiv 0 \pmod{809}$

$\zeta(-543) \equiv 0 \pmod{811}$

$\zeta(-743) \equiv 0 \pmod{821}$

$\zeta(-101) \equiv 0 \pmod{827}$

$\zeta(-65) \equiv 0 \pmod{839}$

$\zeta(-867) \equiv 0 \pmod{877}$

$\zeta(-161) \equiv 0 \pmod{881}$

$\zeta(-417) \equiv 0 \pmod{887}$

$\zeta(-519) \equiv \zeta(-819) \equiv 0 \pmod{929}$

$\zeta(-155) \equiv 0 \pmod{953}$

$\zeta(-165) \equiv 0 \pmod{971}$

$\zeta(-473) \equiv 0 \pmod{1061}$

$\zeta(-887) \equiv 0 \pmod{1091}$

$\zeta(-793) \equiv 0 \pmod{1117}$

$\zeta(-347) \equiv 0 \pmod{1129}$

$\zeta(-533) \equiv \zeta(-783) \equiv \zeta(-967) \equiv 0 \pmod{1151}$

$\zeta(-801) \equiv 0 \pmod{1153}$

$\zeta(-261) \equiv 0 \pmod{1193}$

$\zeta(-675) \equiv 0 \pmod{1201}$

$\zeta(-783) \equiv \zeta(-865) \equiv \zeta(-1117) \equiv 0 \pmod{1217}$

$\zeta(-783) \equiv 0 \pmod{1229}$

$\zeta(-873) \equiv 0 \pmod{1237}$

$\zeta(-517) \equiv 0 \pmod{1279}$

$\zeta(-509) \equiv 0 \pmod{1283}$

$\zeta(-205) \equiv \zeta(-823) \equiv 0 \pmod{1291}$

$\zeta(-201) \equiv \zeta(-219) \equiv 0 \pmod{1297}$

$\zeta(-175) \equiv 0 \pmod{1301}$

$\zeta(-381) \equiv \zeta(-851) \equiv 0 \pmod{1307}$

$\zeta(-303) \equiv 0 \pmod{1319}$

$\zeta(-465) \equiv 0 \pmod{1327}$

$\zeta(-233) \equiv 0 \pmod{1367}$

$\zeta(-265) \equiv 0 \pmod{1381}$

$\zeta(-357) \equiv 0 \pmod{1409}$

$\zeta(-995) \equiv 0 \pmod{1429}$

$\zeta(-573) \equiv 0 \pmod{1439}$

$\zeta(-223) \equiv 0 \pmod{1483}$

$\zeta(-93) \equiv 0 \pmod{1499}$

$\zeta(-1309) \equiv 0 \pmod{1523}$

$\zeta(-861) \equiv 0 \pmod{1559}$

$\zeta(-841) \equiv 0 \pmod{1597}$

$\zeta(-1355) \equiv 0 \pmod{1609}$

$\zeta(-171) \equiv 0 \pmod{1613}$

$\zeta(-559) \equiv 0 \pmod{1619}$

$\zeta(-979) \equiv 0 \pmod{1621}$

$\zeta(-717) \equiv 0 \pmod{1637}$

$\zeta(-269) \equiv \zeta(-1507) \equiv 0 \pmod{1663}$

$\zeta(-387) \equiv \zeta(-1085) \equiv 0 \pmod{1669}$

$\zeta(-29) \equiv 0 \pmod{1721}$

$\zeta(-809) \equiv \zeta(-941) \equiv 0 \pmod{1733}$

$\zeta(-711) \equiv 0 \pmod{1753}$

$\zeta(-1519) \equiv 0 \pmod{1759}$

$\zeta(-1191) \equiv 0 \pmod{1777}$

$\zeta(-1605) \equiv 0 \pmod{1787}$

$\zeta(-847) \equiv \zeta(-1441) \equiv 0 \pmod{1789}$

$\zeta(-549) \equiv \zeta(-697) \equiv \zeta(-1519) \equiv 0 \pmod{1811}$

$\zeta(-1273) \equiv 0 \pmod{1831}$

$\zeta(-953) \equiv \zeta(-1015) \equiv \zeta(-1557) \equiv 0 \pmod{1847}$

$\zeta(-1793) \equiv 0 \pmod{1871}$

$\zeta(-1025) \equiv 0 \pmod{1877}$

$\zeta(-1259) \equiv 0 \pmod{1879}$

$\zeta(-241) \equiv 0 \pmod{1889}$

$\zeta(-1721) \equiv 0 \pmod{1901}$

$\zeta(-1057) \equiv \zeta(-1319) \equiv 0 \pmod{1933}$

$\zeta(-1655) \equiv 0 \pmod{1951}$

$\zeta(-147) \equiv 0 \pmod{1979}$

$\zeta(-509) \equiv 0 \pmod{1987}$

$\zeta(-911) \equiv 0 \pmod{1993}$

$\zeta(-771) \equiv \zeta(-1887) \equiv 0 \pmod{1997}$

$\zeta(-59) \equiv \zeta(-599) \equiv 0 \pmod{2003}$

$\zeta(-1203) \equiv 0 \pmod{2017}$

$\zeta(-1299) \equiv 0 \pmod{2039}$

$\zeta(-1931) \equiv 0 \pmod{2053}$

$\zeta(-375) \equiv \zeta(-1297) \equiv 0 \pmod{2087}$

$\zeta(-1229) \equiv 0 \pmod{2099}$

2017は素数なので，素数にまつわる非自明な特徴がたくさん見つけられそうですね！
2017年も楽しめそうです。

それでは今日はこの辺で。

10000以下の非正則素数のリスト

今回のような非正則素数ハンティングをしたくても，非正則素数のリストってあんまり見つからないのですよね。私は自力で計算しました。みなさんも楽しめるように，10000以下のリストを以下に載せておきました。よかったら使ってください。

http://tsujimotter.info/works/riemann_zeta_leftside/irregular_primes_1-10000.csv

なお，表からわかるように 2017 は 123 番目の非正則素数です。

参考資料

今回の話に興味を持った方はぜひこちらも。

クンマーの合同式とゼータ関数の左側 - 数学カフェ #mathcafe_height from Junpei Tsuji

www.slideshare.net

おまけ：ほかにも2017のあれこれ

2017年になりましたので「2017 という素数がつくる多角形のなかまたち」を３つまとめました。よろしければ新年のご挨拶のネタにお使いください ^_^
（詳しい解説はこちら https://t.co/3cvCrFn7CO ） pic.twitter.com/RzOChN6zR0
— tsujimotter ロマ数本好評発売中!! (@tsujimotter) 2016年12月31日

2017 をいろんな二次形式で表現してみました！https://t.co/Lr0nkrgsGx pic.twitter.com/SyVUp7VMuG
— tsujimotter ロマ数本好評発売中!! (@tsujimotter) 2017年1月1日