数論の勉強をしていく中で、スキーム理論の言葉で書かれた文章をたびたび見かけるようになり、スキームの基礎的な事項について理解したいと思うようになりました。
代数幾何学の標準的な(?)教科書であるハーツホーン [文献1] などの本を読んで、基本的な部分についてはある程度理解してきた気がしているのですが、やはり自分の文章でまとめてみないとわかった気がしません。そこで、今まで理解した部分をブログでまとめてみようと思いました。
そこで今日は、スキーム理論の基本である「アフィンスキーム」について、解説を試みたいと思います。私の理解向上のためというのが目的なので、あくまで自分のために文章化し、それを人にも見てもらえるような場所に置いておくという程度のスタンスで書いています。「みんなにスキームについてわかりやすく教えてやるぜ」というつもりはまったくありません。勘違いしている記述もあると思っています。おかしなところがあれば(こっそりと*1)ご指摘いただければと思います。
「代数幾何学」という、図形を代数的に取り扱う学問があります。代数幾何的な手法を、数論的な対象に対してもより広く適用できるようにするためにスキームが導入されたという話を聞いたことがあります。スキームの発明者は、あの グロタンディーク だそうで、グロタンディークらが発展させたのが数論的な対象を幾何的な道具を使って理解する数論幾何という一分野です。
今回の記事では、①アフィンスキームを定義すること、②アフィンスキームを用いた整数論の見え方について紹介すること、を目的としたいと思います。
とはいえ、そもそもアフィンスキームは、定義するだけでも大変なものです。そこで、ブログ記事を3部構成に分けて、以下のような流れで順を追って説明していきたいと思います。
第1部(本記事):
1. 代数幾何の基本
2. 環のスペクトル
3. ザリスキー位相第2部(5/7公開予定):
4. 構造層
5. アフィンスキームの定義第3部(5/8公開予定):
6. アフィンスキームの射
7. アフィンスキームの射の具体例
8. まとめ
まずアフィンスキームの定義には、環のスペクトルという「環の素イデアルだけで構成された空間」を考える必要があります。一方で、初学者である私の率直な感想としては、なぜそんなものを考えるのかよくわかりませんでした。
そこで第1部では、代数幾何学の基本的なところを触れつつ、流れをざっと追うことで、なぜ環のスペクトルを考えるのかについて考察したいと思います。
その後、第1部の後半と第2部では、アフィンスキームの定義に必要な2つの概念「ザリスキー位相」「構造層」について説明します。これでようやくアフィンスキームが定義できるようになります。
第3部では、アフィンスキームの例をいくつか出した上で、アフィンスキームの間の射について触れたいと思います。これによって、アフィンスキームの言葉を使って、これまでブログでも扱ってきた整数論のいくつかの問題を、少し新しい見方で見ることができるという例を紹介したいと思います。
なお、一連の記事では、可換環と言ったら単位的可換環(単位元 1 を持つ可換環)を考えます。
本記事の目次:
1. 代数幾何の基本
スキームに行く前の準備として、代数幾何の最初に教わる基本的な概念について、簡単に触れておきたいと思います。これにより、スキームを導入するモチベーションが自然に見えてくると思うからです。
代数多様体
代数幾何における主役は代数的に定義される図形です。具体例としては、「円」のような図形を思い浮かべてみるとよいでしょう。円は、 という式で表される図形のことでした。
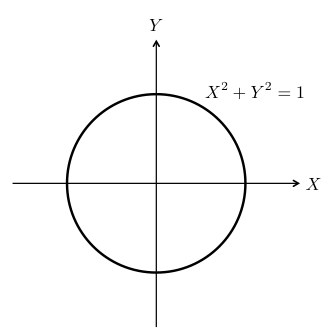
このような直感的な図形観を、もう少し代数幾何的に書き表すことを試みましょう。
代数閉体 を一つ固定します(たとえば
などの体を思い浮かべてください)。
図形を定義する舞台として、アフィン空間を として定義します。要するに、
の値を座標に持つ
次元空間です。アフィン空間の元
のことを座標といいます。
の部分集合で、
変数多項式
に対して
を満たす点
全体の集合(これを
の零点集合といいます)のことを 代数的集合 といいます。
より正確には、代数的集合は 変数多項式環
のイデアル
に対して定義されます。
に対応する代数的集合とは、イデアル
に属する任意の多項式の零点集合の共通部分のことです。これを
と表記することにしましょう。
たとえば、イデアル が
のように単項イデアルによって表される場合、
の任意の元は
を用いて
とかけますから、対応する代数的集合
は
の零点集合です。
イデアルとして のような単項でないものを考えてみましょう。対応する代数的集合は
のそれぞれが作る代数的集合
の共通部分 となります。要するに連立方程式の解ですね。

円を代数幾何的に定義すると、2変数多項式環 を考えて、
のイデアル
に対応する代数的集合
ということができます。
いろいろ難しく書きましたが、要するに「多項式をたくさん並べて、それぞれの零点集合の共通部分をとったもの」のことを代数的集合というわけです。
代数的集合の中で、特にイデアルが素イデアルに対応するものを 代数多様体 といいます。イデアルが単項イデアル ならば、
が既約多項式のとき
は素イデアルなので、そのような
に対応する
は代数多様体となります。
このあたりで薄々感じてくると思うんですが、代数幾何って難しいと思うんですよね。代数的整数論の導入時に大変苦戦したイデアルという概念が、代数幾何では当たり前に登場するからです。
座標環
上で定義した代数多様体の上の関数を考えます。ここでいう関数というのは、座標を変数に持つ多項式のことです。
たとえば、円 だったら
という関数を考えることができますね。
は各点の
座標を返す関数です。
という関数を考えてもいいでしょう。これは
上のすべての点に対して、定数
を返す関数になりますね。
こういうような代数多様体上の点に対して の値を定める関数を考えるためにはどうすればよいでしょう。
代数多様体 を定めるイデアルを
としたとき、多項式環
を
で割ってできる環
を考えます。実はこれが
上の関数全体の集合になります。
この のことを 座標環 といいます。個人的には、この座標環という名前はあまりピンときていません。関数環ならわかるのに。でも名前が付いているなら仕方ないですね。
また円の例で考えてみましょう。 とし、対応する座標環を
とします。
の元として
があります。これは
ですから、円上の関数として定数関数 であることが表現されていますね。
ヒルベルトの零点定理
これまで代数多様体 とその上の座標環
を考えてきました。代数多様体と座標環の間には、密接な関係があるという思想が代数幾何にはあります。そのことを示唆するのが、次に紹介するヒルベルトの零点定理です。
座標環 の極大イデアルについて考えると、
として
という形のものしか存在しないことがわかります。
というのも、 は代数閉体なので、多項式はすべて1次式の積に分解されるからです。したがって、2次以上の多項式は極大イデアルにはなりえません。また、
のような包含関係も成り立つので、極大イデアルの生成元の個数は最大数の
個になるはずです。*2
このように、 と
の極大イデアルの全体
の間に
なる全単射が存在するということを主張するのが、ヒルベルトの零点定理 です。正確に言えば、このステートメントはヒルベルトの零点定理の弱系と呼ばれるものです。
ヒルベルトの零点定理によれば、座標環の極大イデアルは代数多様体の座標だと思うことができるというわけですね。このことは
という発想につながります。この辺りの観察が、アフィンスキームの定義につながっていくのだと私は理解しています。
2. 環のスペクトル
多項式環 のイデアル
に対応する代数多様体
と、
上の関数全体の集合である座標環
を考えました。そして、
と
の極大イデアル全体
の対応関係から、
の方を空間だと思おうという発想の転換について述べました。
上では、座標環 としては代数閉体上の多項式(の剰余環)だけを考えましたが、これをもっと一般的な可換環
としたい。たとえば、
として代数閉体ではない体
(たとえば
など)に対して
を考えてみます。このようにすると、
上定義された曲線などを扱うことができます。このように拡張することで、代数曲線の有理点の問題など、数論的な対象も取り扱えるようになるでしょう。
ほかにも、 みたいなものを考えることもします。これは整数環
の元が関数だと思えるような空間を考えていることになります。少しぎょっとしますが、あとで具体的に扱っていきましょう。
可換環 に一般化するにあたって、極大イデアルだけでなく素イデアルも考えることにします。
の素イデアル全体の集合を
としましょう。
を環
のスペクトルといいます。次の節では、この
が位相空間であるということを説明をします。
具体例を考えてみましょう。
とします。
の素イデアル全体の集合
は次のようになるでしょう。
以外はすべて素数
の単項イデアル
となっていますね。

3. ザリスキー位相
上で定義した に位相を入れて位相空間にしましょう。これから紹介するのは
の ザリスキー位相 と呼ばれるものですが、開集合系によって定義されます。
を
のイデアルとします。
これは の部分集合になり、特に
を含まない素イデアル
全体の集合となります。
を任意のイデアルとしたときの
の全集合は、開集合系の公理を満たすことが(調べれば)わかります。これがザリスキー位相です。
として
のザリスキー位相を考えましょう。
は単項イデアル整域なので、
として、
を計算することにします。
の場合、
です。
まず、 は
を含みませんので、
です。
(3の倍数全体)は
(15の倍数全体)を含みますので、
です。
(5の倍数全体)も
(15の倍数全体)を含みますので
です。
それ以外の素イデアル は
を含みませんので、
に対して
です。
したがって、 は
となります。(すなわち、 以外の素イデアル全体です。)
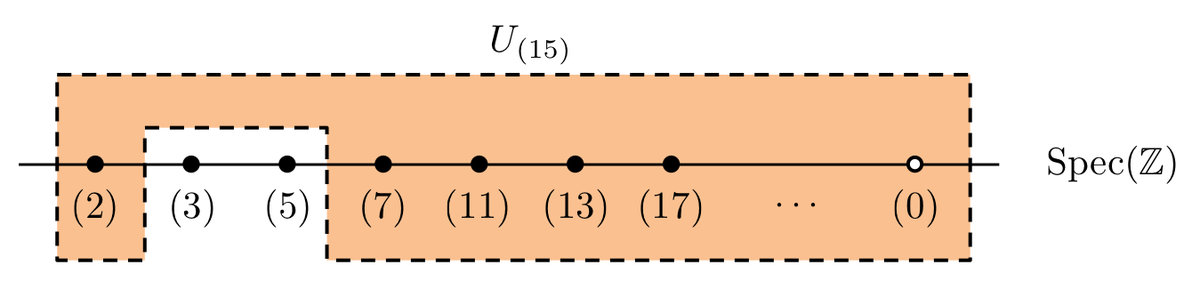
また、同様に は
となります。(すなわち、 以外の素イデアル全体です。)
は(
より)
となります。(すなわち、 以外の素イデアル全体です。)
の定義は
ですから、 はすべての素イデアルに含まれます。よって、
です。
の定義は
ですが、 を含む素イデアルはありません。よって、
は全集合
です。
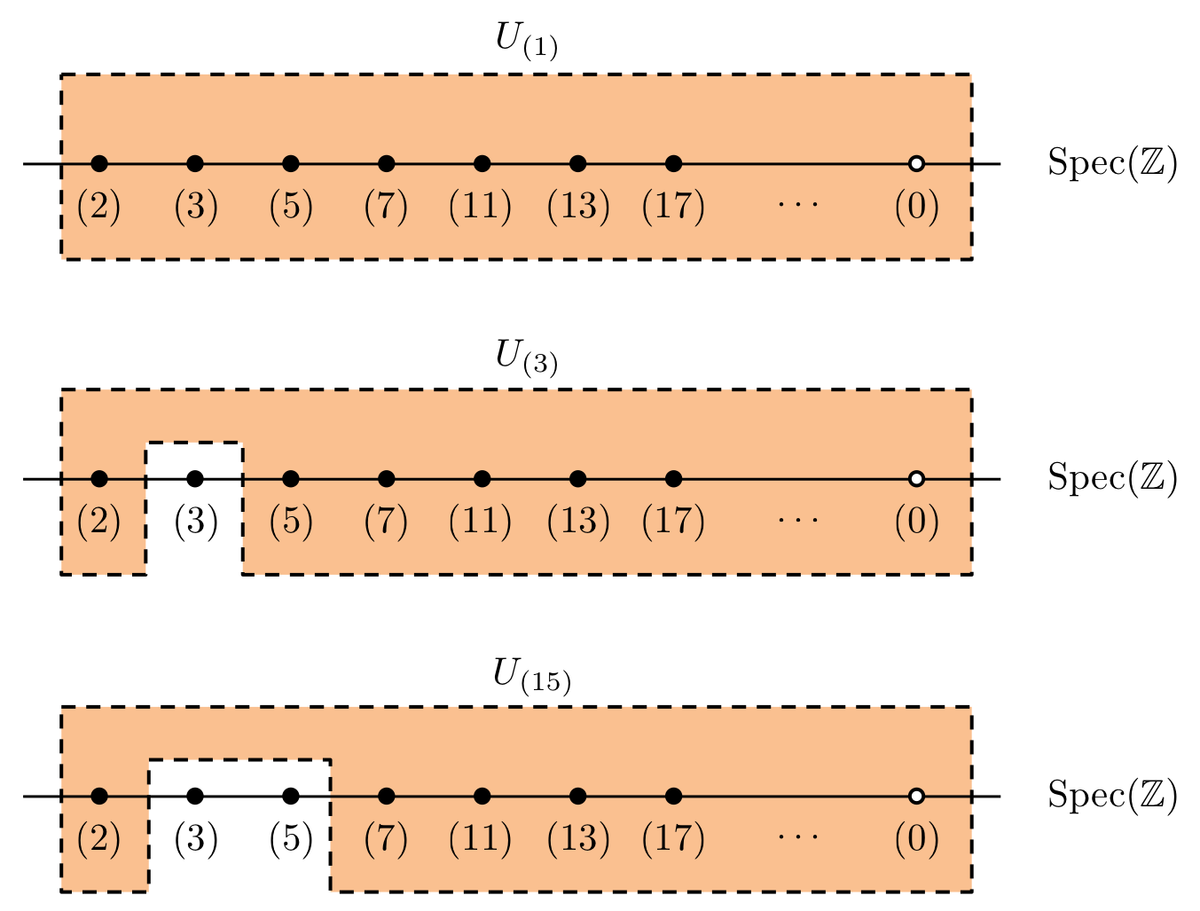
以上をまとめると、
- 全集合
と空集合
を開集合に持つ
- 開集合の任意の合併は開集合
- 開集合の有限個の共通部分は開集合
という性質を満たすことがわかり、位相空間における開集合の公理を満たします。
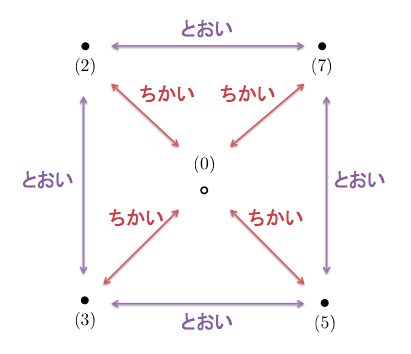
また、 だけを含む開集合はありません。空集合を除くすべての開集合は
を含むという特徴もわかりました。つまり、
と
を分離する近傍がありません。すなわち、ハウスドルフ空間ではないということです。
は空集合以外のすべての開集合に含まれるので、直感的には
はどの点に対しても平等に近く、それ以外の点同士は同じくらい遠いような空間となっています。
おわりに
今日は、環のスペクトル を定義して、
にザリスキー位相を入れて位相空間としました。素イデアルを点だと思って、素イデアル全体の集合を図形とみなすという発想は、初めてアフィンスキームについての話を知ったときに面白いと思ったことでした。
次回(5/7公開予定)は、 の上の構造層を考えて、いよいよアフィンスキームを定義します。
それでは今日はこの辺で。
第2回の記事はこちら:
*1:「こっそりと」の意味は「ブログのコメント欄ではなく、TwitterのDM等のクローズドな場所でご指摘下さい」という意味です。コメントで指摘されると、それを直ちに修正するという必要性が生じますが、一方で私の理解を超える高度な指摘は時に考える時間を要します。コメントが公開されたまま直ちに修正できない状況が続くと、私自身がプレッシャーに晒されることになります。趣味で数学の記事を書いている私としては、そのような状況はできるだけを避けたいというのが趣旨です。クローズドな場でご指摘いただくことは、私自身の成長にもつながりますので大歓迎です。ぜひ宜しくお願いします。
*2:この辺りの観察が、イデアルの包含関係の個数からクルル次元を定義するっていう発想につながるんですかね。
