虚数乗法論 (2)：楕円曲線の由来 - tsujimotterのノートブック

虚数乗法シリーズ、第２回目です。

シリーズの記事は、こちらのタグから検索ください。
tsujimotter.hatenablog.com

今日は、楕円曲線の基本的な事項についてお話します。この記事を読んだら、楕円曲線の由来が楕円関数からきていることが納得できるかと思います。

また、度々言及される「楕円曲線はトーラスの形をしている」ということの意味について解説したいと思います。

ワイエルシュトラスのペー関数

高校で習う三角関数は周期を持つ関数でした。つまり、任意の $x$ に対して

$f(x + \omega) = f(x)$

を満たす周期 $\omega$ が存在するような関数です。

複素関数においては

$f(z + \omega_1) = f(z + \omega_2) = f(z) \tag{3}$

のように、２つの周期 $\omega_1, \omega_2$ を持つものも存在します。このような周期のことを２重周期といい、２重周期を持つ複素関数のことを楕円関数といいます。

式 $(3)$ の２重周期の性質から

$\cdots = f(z - 2\omega_1) = f(z - \omega_1) = f(z) = f(z + \omega_1) = f(z + 2\omega_1) = \cdots$

$\cdots = f(z - 2\omega_2) = f(z - \omega_2) = f(z) = f(z + \omega_2) = f(z + 2\omega_2) = \cdots$

が成り立つことがすぐにわかります。あるいは、これを組み合わせて

$f(z + m\omega_1 + n\omega_2) = f(z) \tag{3}$

も任意の整数 $m, n$ について成り立ちます。 $z$ にちょうど「格子状の点」を足し合わせても、関数の形が変わらないのです。

このような発想から、 $\mathbb{C}$ の格子と呼ばれる集合が自然に導入されます。

定義（格子）

$\mathbb{C}$ の格子とは，２つの複素数 $\omega_1, \omega_2$ を用いて

$\Lambda = \mathbb{Z}\omega_1 + \mathbb{Z}\omega_2 = \{ m \omega_1 + n \omega_2 \mid m, n \in \mathbb{Z} \} \tag{4}$

と表される複素数体 $\mathbb{C}$ の部分集合で， $\mathbb{Z}$ を $\mathbb{R}$ に置き換えたときに $\mathbb{C}$ に一致するものを言う．

格子の例をいくつか紹介しましょう。左側が周期として $\omega_1 = 1, \; \omega_2 = \sqrt{-1}$ をとった格子で、右側が周期として $\omega_1 = 1, \; \omega_2 = \frac{1+\sqrt{-3}}{2}$ をとった格子です。

f:id:tsujimotter:20180520085101p:plain:w500

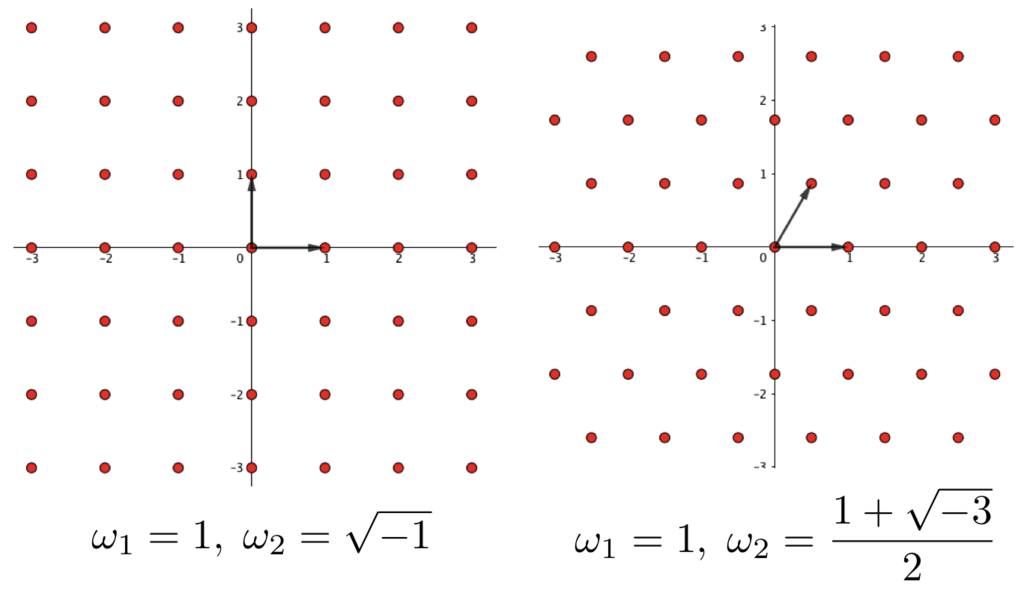
「 $\mathbb{Z}$ を $\mathbb{R}$ に置き換えたときに $\mathbb{C}$ に一致する」の意味が捉えづらいかもしれませんが、これは $\omega_1, \omega_2$ が（ $\mathbb{R}$ ベクトル空間としての） $\mathbb{C}$ の基底になっているということです。たとえば $\omega_1 = \sqrt{2} \omega_2$ のように片方が他方の実数倍になってしまうと、 $\mathbb{R}\omega_1 + \mathbb{R}\omega_2$ は1次元の空間になってしまって、 $\{\omega_1, \omega_2\}$ は $\mathbb{C}$ の基底となりません。

楕円関数の一般論を展開したところで、本題のワイエルシュトラスのペー関数を紹介しましょう。ペー関数 $\wp(z; \Lambda)$ は、以下のように定義されます。

定義（ワイエルシュトラスのペー関数）

$\Lambda \subset \mathbb{C}$ を $\mathbb{C}$ の格子としたとき，複素変数 $z$ に対してペー関数 $\wp(z; \Lambda)$ は以下の式で定義される：

$\displaystyle \wp(z; \Lambda) = \frac{1}{z^2} + \sum_{\lambda \in \Lambda \backslash \{0\}}\left\{ \frac{1}{(z-\lambda)^2} - \frac{1}{\lambda^2} \right\} \tag{5}$

$\mathbb{C}$ の格子 $\Lambda$ が文脈から明らかである場合は，単に $\wp(z)$ と略記する．

$\Lambda \backslash \{0\}$ は、格子 $\Lambda$ から点 $0$ を除いた集合のことです。 $\lambda = 0$ を入れると、式 $(5)$ の後半にある $1/\lambda^2$ が発散してしまいますので、あらかじめ除いておく必要があります。

定義が複雑に見えますが、格子 $\Lambda$ の元を丁寧にばらせば

$\displaystyle \begin{align}\wp(z) = \frac{1}{z^2} &+\left\{ \frac{1}{(z-\omega_1)^2} - \frac{1}{\omega_1^2} \right\} \\ &+\left\{ \frac{1}{(z-\omega_2)^2} - \frac{1}{\omega_2^2} \right\} \\ &+\left\{ \frac{1}{(z-(-\omega_1))^2} - \frac{1}{(-\omega_1)^2} \right\} \\ &+\left\{ \frac{1}{(z-(-\omega_2))^2} - \frac{1}{(-\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-2\omega_1)^2} - \frac{1}{(2\omega_1)^2} \right\} \\ &+\left\{ \frac{1}{(z-2\omega_2)^2} - \frac{1}{(2\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-(-2\omega_1))^2} - \frac{1}{(-2\omega_1)^2} \right\} \\ &+\left\{ \frac{1}{(z-(-2\omega_2))^2} - \frac{1}{(-2\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-(\omega_1+\omega_2))^2} - \frac{1}{(\omega_1+\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-(-\omega_1-\omega_2))^2} - \frac{1}{(-\omega_1-\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-(-\omega_1+\omega_2))^2} - \frac{1}{(-\omega_1+\omega_2)^2} \right\} \\ &+\left\{ \frac{1}{(z-(\omega_1-\omega_2))^2} - \frac{1}{(\omega_1-\omega_2)^2} \right\} \\ &+ \cdots \end{align}$

という形の和によって表されることが理解できるかと思います。

ペー関数は楕円関数の仲間で、格子 $\Lambda$ のパラメータ $\omega_1, \omega_2$ がそのまま２重周期になります。

この $\wp$ という文字は「ペー」と呼びます。LaTeX の数式では \wp と打つことで表示される数学記号です。

ペー関数に親しみを持つために、ペー関数の3Dプロットを作ってみました。

f:id:tsujimotter:20180516143055p:plain:w400

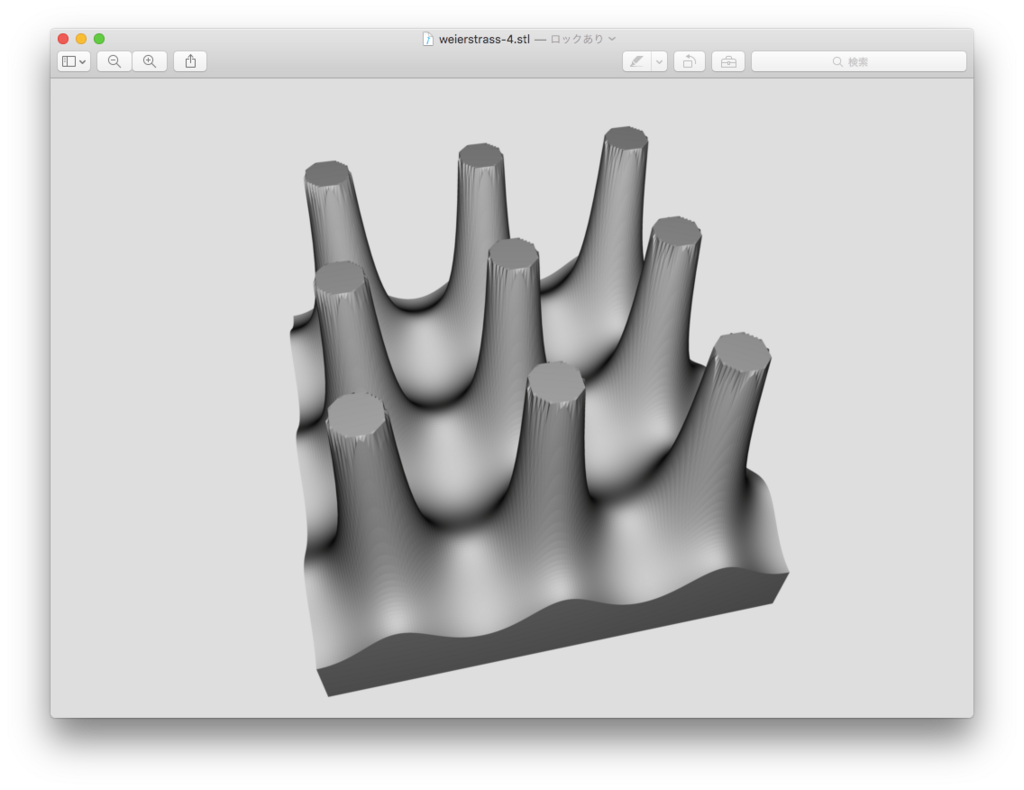
図は $\omega_1 = 3, \; \omega_2 = 3\sqrt{-1}$ としたときの例で

$-4.5 \leq \text{Re}\,z \leq 4.5, \;\; -4.5 \leq \text{Im}\,z \leq 4.5$

の範囲で、 $\wp(z)$ の絶対値 $|\wp(z)|$ を表示しています。

$\wp(z)$ の「極」が図の中心、つまり $z = 0$ にあることがわかります。 $z = 0$ だけでなく、格子の点上（ $3m+3n\sqrt{-1}$ ）の位置に極がありますね。
また、２重周期性も見てとれます。 $z = 0$ から $3+3\sqrt{-1}$ の四角形を基本領域として、これを繰り返し並べたような形状になっています。基本領域の範囲でプロットをたくさんつくって無限に並べていけば、複素数平面を埋めつくすことができます。

楕円曲線の標準形とトーラス

ペー関数を準備しましたので、ようやくですが楕円曲線との関連を見ることができます。

まず、ペー関数は以下のように $z = 0$ の周りで展開することができます。

$\displaystyle \wp(z) = \frac{1}{z^2} + \frac{g_2}{20}z^2 + \frac{g_3}{28}z^4 + \cdots \tag{6}$

ここで、 $g_2(\Lambda), g_3(\Lambda)$ は格子に対して決定される楕円不変量と呼ばれるパラメータなのですが、定義は次の通りです：

$\displaystyle g_2 = 60 \sum_{\lambda \in \Lambda \backslash \{0\}} \frac{1}{\lambda^4}$

$\displaystyle g_3 = 140 \sum_{\lambda \in \Lambda \backslash \{0\}} \frac{1}{\lambda^6}$

知っている人のために説明すると、この式は少し書き換えるとアイゼンシュタイン級数という保型形式になっています。

$\lambda = m\omega_1 + n\omega_2$ として明示的に書くと

$\displaystyle \sum_{\lambda \in \Lambda \backslash \{0\}} \frac{1}{\lambda^6} = \sum_{(m, n) \in \mathbb{Z}^2\backslash \{(0, 0)\}} \frac{1}{(m\omega_1 + n\omega_2)^4}$

となり、 $\tau = \omega_1 / \omega_2$ （ただし、 $\text{Im}\,\tau > 0$ となるようにとる）とすると

$\displaystyle \begin{align} &= \sum_{(m, n) \in \mathbb{Z}^2\backslash \{(0, 0)\}} \frac{\omega_2^4}{(m\omega_1/\omega_2 + n)^4} \\ &= \omega_2^4 \sum_{(m, n) \in \mathbb{Z}^2\backslash \{(0, 0)\}} \frac{1}{(m\tau + n)^4} \\ &= \omega_2^4 E_4(\tau) \end{align}$

となり、 $E_4(\tau)$ はアイゼンシュタイン級数ですね。

さて、これを変数 $z$ で微分すると

$\displaystyle \wp'(z) = -\frac{2}{z^3} + \frac{g_2}{10}z + \frac{g_3}{7}z^3 + \cdots \tag{7}$

が得られます。

式 $(6), (7)$ をじっと睨むと、以下の式が成り立っていることが確認できます。*1

$\displaystyle (\wp'(z))^2 = 4(\wp(z))^3 - g_2 \wp(z) - g_3 \tag{8}$

これはペー関数の微分方程式になっています。

ここでもし

$\begin{cases} x = \wp(z) \\ y = \wp'(z) \end{cases}$

とおけば

$\displaystyle y^2 = 4x^3 - g_2 x - g_3 \tag{8}$

という式が得られます。

これはまさに楕円曲線の定義方程式になっています！！

もしかすると、楕円曲線の定義方程式といえば、こちらの式で覚えている方も多いかもしれません。

$\displaystyle y^2 = x^3 + ax + b \tag{9}$

この形の式をワイエルシュトラスの標準形と言います。式 $(8)$ に $x \leftarrow x/36, \; y \leftarrow y/108$ を代入してあげれば、この標準形に変形できますので安心してください。

変数変換によって $a, b \in \mathbb{C}$ であるような標準形に変形可能な代数曲線のことを $\mathbb{C}$ 上の楕円曲線といいます *2。「 $\mathbb{C}$ 上の」という文言は「 $\mathbb{C}$ 上定義された」の意味で、 $/\mathbb{C}$ と書くことが多いです（「オーバーシー」と読みます）。

また、 $\mathbb{C}$ 上の楕円曲線において、座標 $(x, y)$ がともに $x, y \in \mathbb{C}$ である点を $\mathbb{C}$ -有理点といい、 $\mathbb{C}$ -有理点全体の集合を $E(\mathbb{C})$ と表記します。 $K \subset \mathbb{C}$ に対しても同様に $K$ -有理点を定義できて、その集合を $E(K)$ と表記します。今日はあとで $E(\mathbb{R})$ がでてきます。

さて、ここまでで重大な結果を得ることができました。

ワイエルシュトラスのペー関数 $\wp, \wp'$ は複素数平面 $\mathbb{C}$ 上の関数でした。その行き先 $(\wp, \wp')$ が、（適切に変数変換を施せば） $\mathbb{C}$ 上の楕円曲線 $E: y^2 = x^3 + ax + b$ と対応しているというのです。

もう少し正確に言えば、ペー関数 $\wp(z), \wp'(z)$ は２重周期関数ですから、格子の分だけずらしたものは同じ値に対応します。したがって $z$ に対して楕円曲線 $E$ の点が対応しているというよりは、 $z + \Lambda$ に対して楕円曲線 $E$ の $\mathbb{C}$ -有理点 $(\wp(z), \wp'(z))$ が対応していると考えます。

$z + \Lambda \;\; \mapsto \;\; (\wp(z), \wp'(z)) \tag{10}$

左辺は $\mathbb{C}$ の $\bmod{\Lambda}$ の剰余類となり、右辺は $E(\mathbb{C})$ 上の点です。すると

$\mathbb{C}/\Lambda \;\; \longrightarrow \;\; E(\mathbb{C}) \tag{11}$

という対応関係が得られたことになります。この写像が実は全単射になっており、連続性から同相写像となっています。

f:id:tsujimotter:20180520083249p:plain:w400

もう少しだけ格子で割った複素数平面 $\mathbb{C}/\Lambda$ について考えてみましょう。まず、平行四辺形の角に当たる $z = 0$ の点と $z = \omega_1, \; z = \omega_2$ 、それから $z = \omega_1 + \omega_2$ については、２重周期性から、すべて同じ点とみなすことができます。

f:id:tsujimotter:20180519195827p:plain:w240

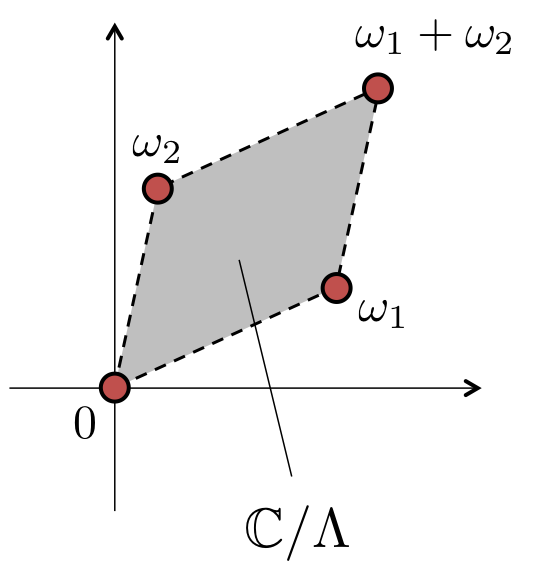
さらに、左端と右端の辺（赤い実線）についても同様の理由で同じ値に対応しています。したがって、両辺はつながっていると思うことができます。上端と下端の辺（青い点線）も同様につながっています。

f:id:tsujimotter:20180519195853p:plain:w240

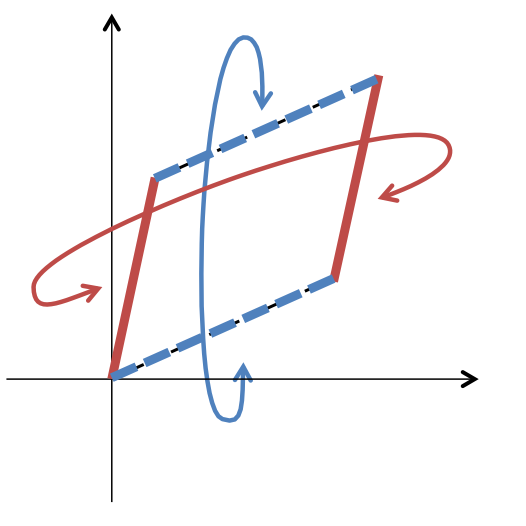
$\mathbb{C}/\Lambda$ は、まさに「ドラゴンクエストの世界地図」のような世界になっているわけです。このような世界は、トポロジー的にはトーラスと呼ばれる図形となっています。したがって、 $\mathbb{C}/\Lambda$ はトーラスに同相で、さらに $\mathbb{C}/\Lambda$ から $E(\mathbb{C})$ への連続な全単射があることから、 $E(\mathbb{C})$ もトーラスに同相というわけです。

f:id:tsujimotter:20180520083314p:plain:w400

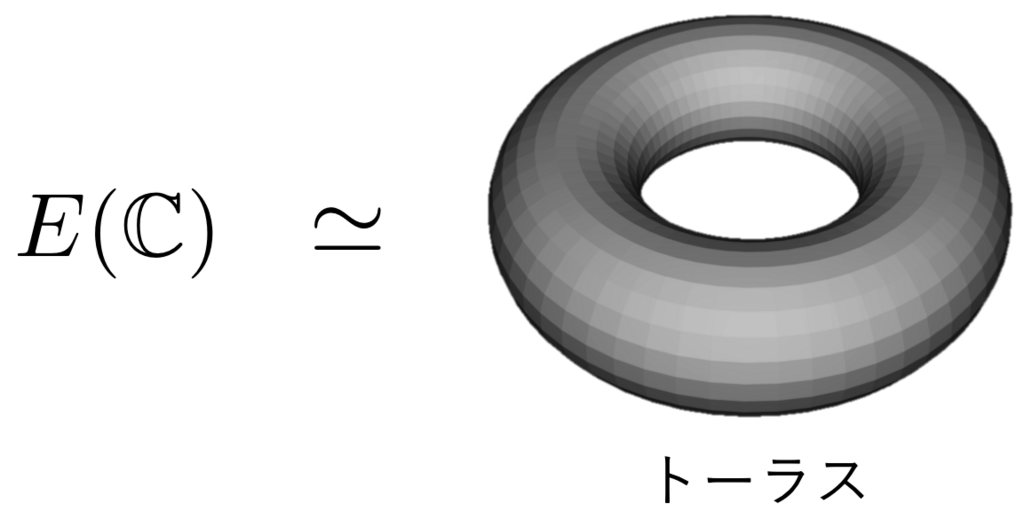
しばしば言われる「楕円曲線はトーラスの形をしている」というのは、このことを意味していたわけですね。

ちなみに、楕円曲線の座標は $(x, y) \in \mathbb{C}^2$ なので、複素数平面を２次元ユークリッド平面で表そうとすると、４次元のユークリッド空間が必要になります。我々は３次元の空間に生きていますので、なかなか想像が難しいですね。もし４次元人に出会ったら、 $\mathbb{C}$ 上の楕円曲線がどんな風に見えるのか聞いてみたいものです。

極と無限遠点

さて、格子で割った複素数平面 $\mathbb{C}/\Lambda$ と $\mathbb{C}$ 上の楕円曲線 $E(\mathbb{C})$ が同相であることがわかりました。

注意深く読んできた方は「ちょっと待て、極はどうするんだ？」と思うかもしれません。 $z = 0$ はペー関数の極に対応しており、発散してしまいます。したがって、そのままでは $\mathbb{C}^2$ の点 $(x, y)$ に対応づけられません。つまり、 $\mathbb{C}$ 上の楕円曲線はトーラスと同相といいつつも、実際のところはトーラスから1点だけが抜け落ちたものを考えてしまっているわけです。

この問題を解消する方法の一つとしては、無限遠点という点を加えるものがあります。つまり、 $\mathbb{C}$ 上の楕円曲線の定義を

$E = \{ (x, y) \mid y^2 = x^3 + ax + b \} \cup \{\mathcal{O}\}$

としてしまえばいいのです。ここで $\mathcal{O}$ は無限遠点です。

しかしここで納得のいかない人もいると思います。「 $\mathcal{O}$ って一体なんなんだ」と。少なくとも私はそう思いました。

この議論を正当化するために射影平面という概念を導入します。

射影平面とは、変数 $x, y, z$ の比 $(x : y : z)$ で表される空間です。おっと、ここで複素数の $z$ と記号がかぶってしまいましたが、ここだけは射影平面の３つ目の変数と思ってください。 $(x : y : z)$ は比なので、 $x, y, z$ をそれぞれ定数倍したものも、同じものとみなされます。

$(c x : c y : c z) = (x : y : z), \;\; \forall c\in \mathbb{C}^\times$

ただし、 $(x : y : z) = (0 : 0 : 0)$ は除きます。

座標 $(x, y, z) \neq (0, 0, 0)$ に上のような同値関係 $(c x, c y, c z) \sim (x, y, z)$ が入っていて、その同値関係 $\sim$ で割った空間と考えても良いでしょう。

3つの変数 $x, y, z$ が複素数 $\mathbb{C}$ の元であるとき、このような空間を複素射影平面といい、 $\mathbb{P}^2(\mathbb{C})$ と表します。*3

$\mathbb{C}^2$ 上の任意の点は、以下のように $\mathbb{P}^2(\mathbb{C})$ に自然に埋め込まれます：

$\mathbb{C}^2 \ni (x, y) \;\; \mapsto \;\; (x : y : 1) \in \mathbb{P}^2(\mathbb{C})$

また

$\mathcal{O} = (0 : 1 : 0)$

を無限遠点として定義します。これで射影平面上に無限遠点が定義できましたね。

したがって、楕円曲線の点は自然に $\mathbb{P}^2(\mathbb{C})$ 上の点と思うことができるというわけです。

1点が空いていたトーラスに無限遠点が追加されて、境界がなくなりました。このような操作を「コンパクト化」といったりします。

f:id:tsujimotter:20180519200634p:plain:w400

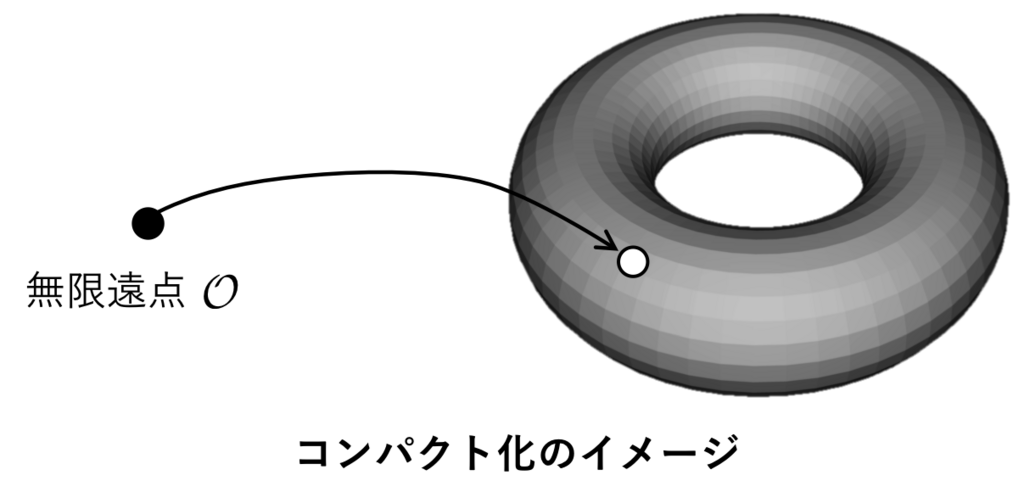
実平面上の点

今後、「楕円曲線」と「格子で割った複素数平面」を対応させることが非常に重要になってきます。このような議論を展開していくためには、やはり $\mathbb{C}/\Lambda$ と $E(\mathbb{C})$ の対応関係をできるだけ具体的にイメージできることが大事です。具体的な例を少し計算してみましょう。

今、 $\omega_1 = 3, \; \omega_2 = 3i$ とします。格子で割った複素数平面 $\mathbb{C}/\Lambda$ の上に、赤と青の２本の線を引いてみました。赤い線は $\text{Im}\,z = 1.5$ 、青い線は $\text{Im}\,z = 0$ を通っています。

f:id:tsujimotter:20180519215834p:plain:w200

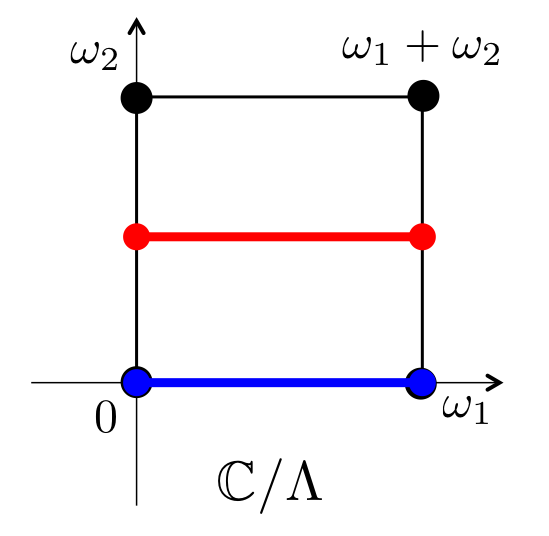
左端と右端は同一視されますので、両方とも境界を持たない「ループ」になっています。この２本のループが、楕円曲線のどこに対応するでしょうか。

計算してみるとわかりますが、この上のペー関数 $\wp(z), \wp'(z)$ の値は実数値になります。したがって、 $x = \wp(z), \; y = \wp'(z)$ とすると、両方とも実数になるので、 $(x, y)$ -平面で表すことができます。これは楕円曲線の $\mathbb{R}$ -有理点の集合で、楕円曲線 $E : y^2 = 4x^3 - g_2 x - g_3$ を $(x, y)$ -平面で表した「よく見かける図」が現れるはずです。*4

実際、赤い方のループを描くと次のように楕円曲線の「たまご型（赤い曲線）」の部分ができます。青い方のループの方は右側の上下に広がる青い曲線になります。

f:id:tsujimotter:20180519203054p:plain:w400

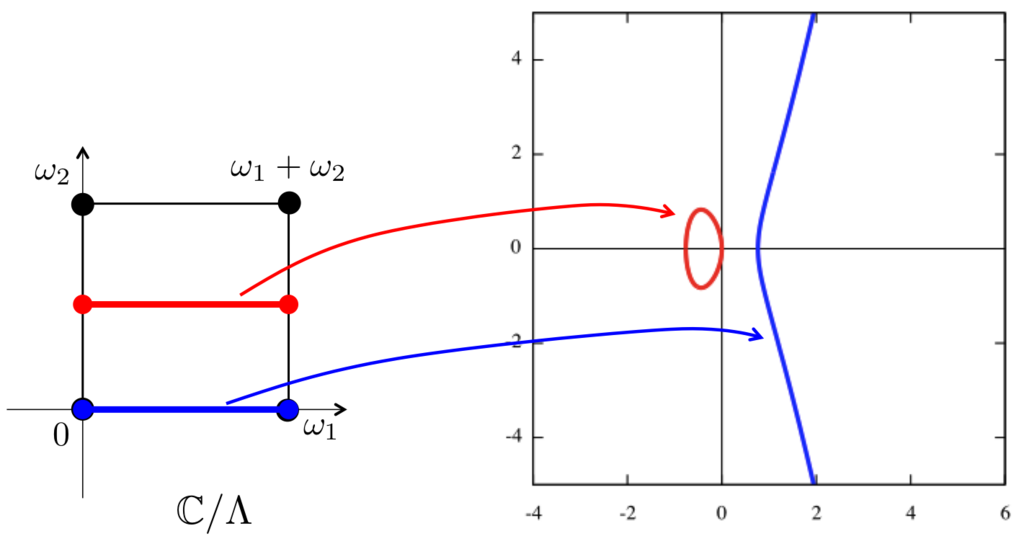
青い線については、 $\mathbb{C}/\Lambda$ の方ではループとなっているのに、楕円曲線の方ではループになっていないように見えます。
しかし、 $z = 0$ の点は、楕円曲線では無限遠点 $\mathcal{O}$ に対応しています。右側の曲線は切れているようで、実はずっと先の無限遠点でつながり、ループになっているのです。イメージ的にはこんな感じです。

f:id:tsujimotter:20180519203121p:plain:w240

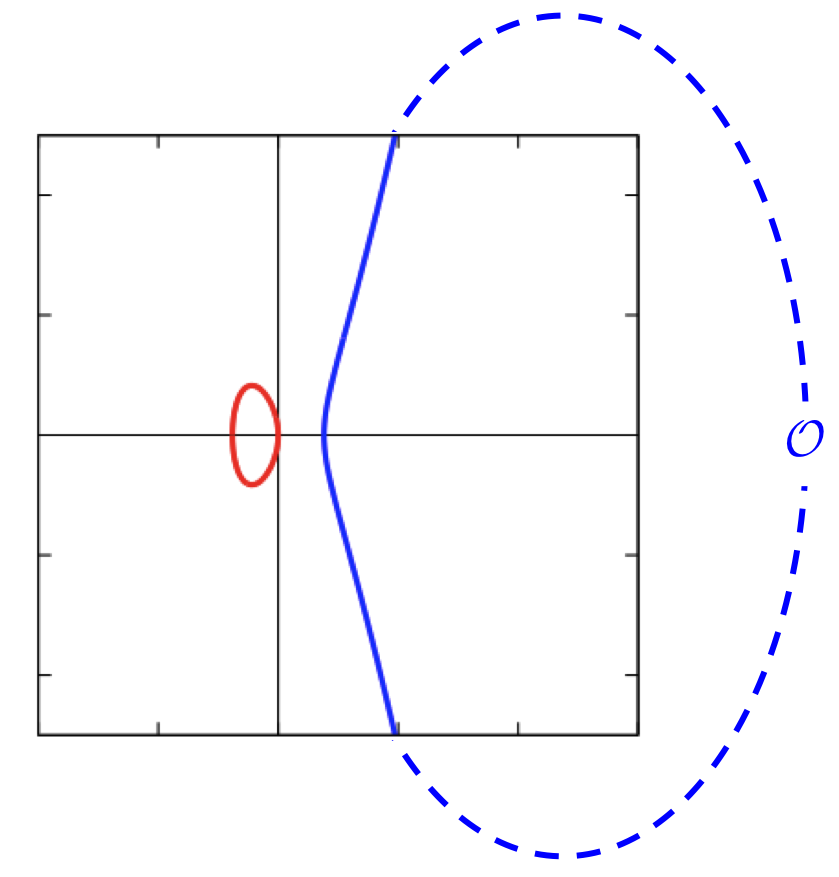
よって、楕円曲線の $(x, y)$ -平面におけるグラフは、実は楕円曲線のトーラスを「輪切り」にしたときの「２つの断面（赤と青の線）」だったというわけです。

f:id:tsujimotter:20180519203141p:plain:w400

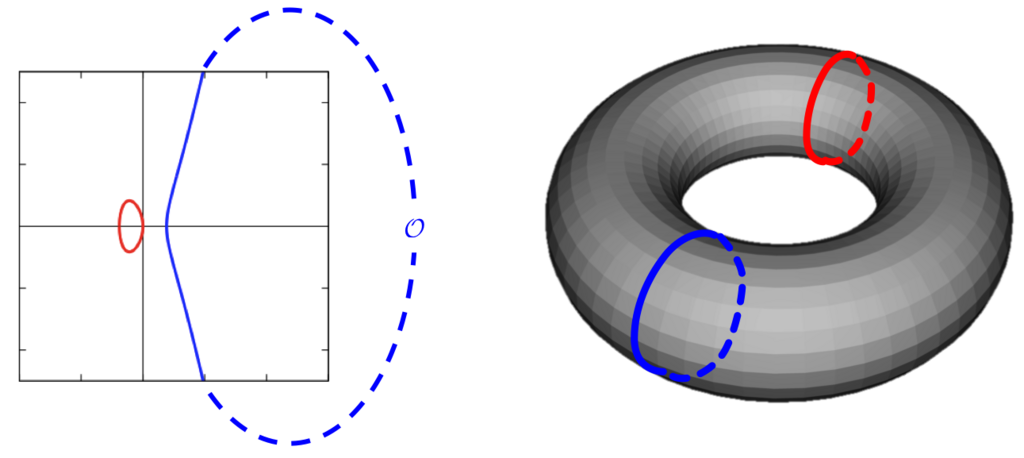
おわりに

ここまでの議論で「複素数平面を格子で割った空間 $\mathbb{C}/\Lambda$ 」と「 $\mathbb{C}$ 上の楕円曲線 $E(\mathbb{C})$ 」が同相であるということを説明してきました。両者を結びつけるのは、ワイエルシュトラスのペー関数という楕円関数でした。このことを「楕円曲線はペー関数によってパラメータ化される」というように言うこともあります。楕円関数によってパラメータ化されるので、「楕円」曲線と名付けられたそうです。これが楕円曲線という名称の由来です。

幾何的な視点でいうと、 $\mathbb{C}$ 上の楕円曲線は「多様体」と見ることもできます。局所座標としては複素数平面 $\mathbb{C}$ になるわけですね。複素1変数の座標を取れる連結な多様体のことを「リーマン面」といいます。よって「 $\mathbb{C}$ 上の楕円曲線はリーマン面である」と言い換えることもできますね。

ここまで理解してもらえたのであれば、もはや $\mathbb{C}$ 上の楕円曲線は $\mathbb{C}/\Lambda$ だと思ってしまっても良さそうです。実際、楕円曲線の代わりに $\mathbb{C}/\Lambda$ を考えることは、虚数乗法を理解するための強力な武器となります。

次回は、今回の議論をもとに、虚数乗法についての理解を深めていきたいと思います。

それでは今日はこの辺で。

*1:[Silverman, AEC, Theorem 3.5, p.169] 参照

*2:正確には「非特異性」の条件が加わりますが、これについてはいずれ触れたいと思います。

*3:肩についている "2" は射影平面、すなわち「2次元」射影空間の意味です。3変数なのに2次元というのは不自然に思うかもしれませんが、このように定義されます。私の考えですが、定数倍で束縛されているので実質自由度が2次元、ということなのではないかと思っています。

*4:今回、私がワイエルシュトラスのペー関数を数値計算した動機は、まさにこの計算がしたかったからです。