虚数乗法シリーズ、第3回目です。
今回は「虚数乗法」という呼び名に納得してもらえるような話をしたいと思います。記事を読み終わったみなさんが、タイトルのような感想を持つことを期待しています。
簡単にあらすじをお話しましょう。
前回、「 上の楕円曲線の
-有理点
」と「格子で割った複素数平面
」が対応していることを学びました。
楕円曲線 を代数側、複素数平面
を解析側と呼ぶことにします。両者をつなぐ写像を解析的同型写像と呼びます。
虚数乗法とは、解析側で考えると単に「(整数でない)複素数(=虚数)を掛けること(=乗法)」だと思うことができます。まさに「虚数」「乗法」です。
楕円曲線の「加法」
解析側 で考える利点として、楕円曲線の「加法」を自然に導入できることが挙げられます。
は複素数平面なので「加法」の構造が入っています。
は
を格子で割ったものなので、自然に加法が誘導されます。
つまり、 に対して
が成立するということです。
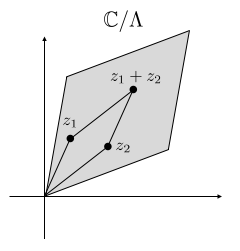
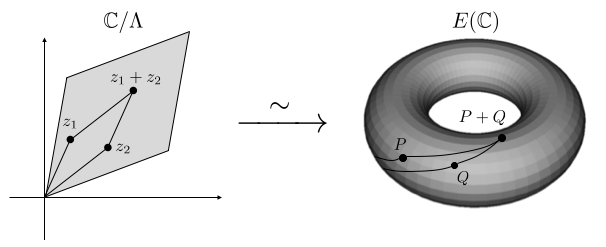
には
からの同相写像を通して、楕円曲線に加法の構造を入れることができます。つまり、楕円曲線上の2点
に対して
のように加法を定義できます。
ただ、このままでは代数側と解析側の対応関係をいちいち調べないと、楕円曲線の加法が計算できません。できれば代数側の情報だけで加法を計算できるようにしたい気持ちがあります。
そこで、ペー関数の加法定理を使います。三角関数に加法定理があったように、楕円関数にも加法定理があるのです。
ここで
とおくと
と表せます。左辺は
同様に の方にも加法定理があり
の座標が
の座標を用いて表せるような式となっています。
上の加法定理の式を幾何的に解釈することもできます。簡単のため の点に限定して考えましょう。
の加法を
と表記すると、
は次のように得られます。
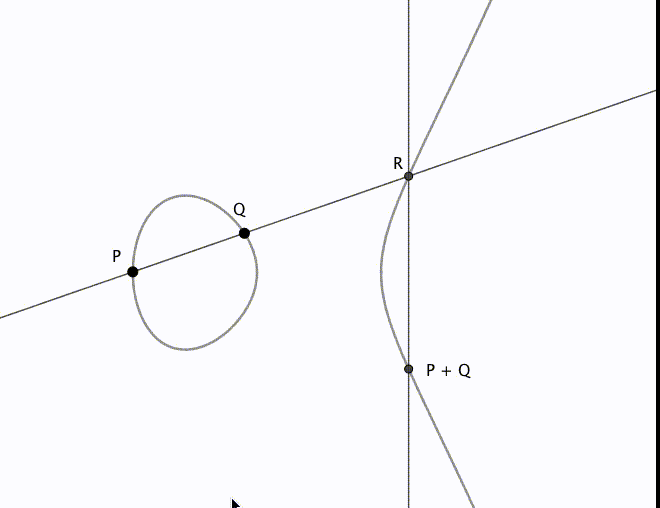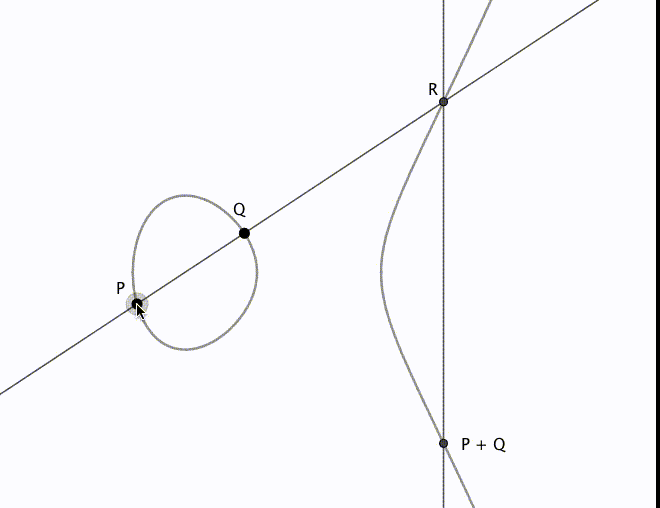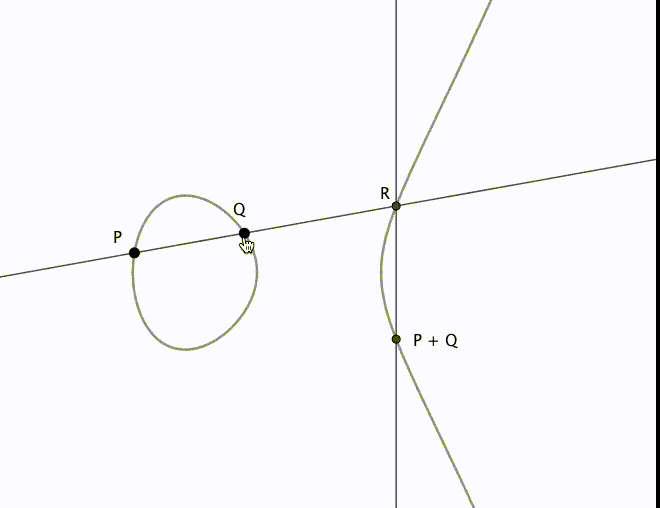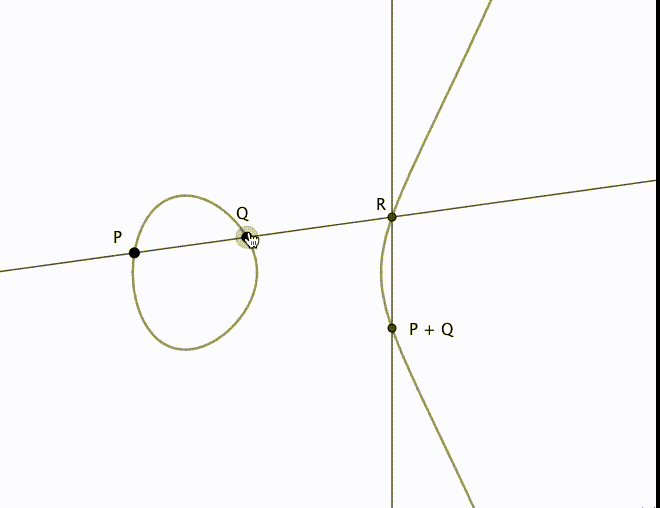
を通る直線と
の交点を
とします。
を
軸対称に折り返したものが
となります。加法定理の式が幾何学的には実際に上のような操作になっていることは、自分で確かめてみると面白いかと思います。
のときは少し注意が必要なのですが、これについてはAECを参照してください *1。
が言えることは一つ覚えておいてほしいことです。楕円曲線の -有理点の集合
は
の部分群となります。
これまでの議論により、楕円曲線 に加法群の構造を入れることができました。したがって、
も
も加法群になったわけですね。第2回の記事で与えた写像
は、単なる同相写像なだけでなく、
の(複素Lie群としての)群同型を与える群同型写像だったというわけです。
 倍写像
倍写像
加法が入ったということは、これを 回繰り返して、
倍写像
を定義することができます。
解析側 の方でも
を整数すれば
倍写像を定義することができます。加法の定義から
の
倍写像は、解析的同型写像を通して
の
倍写像に対応します。
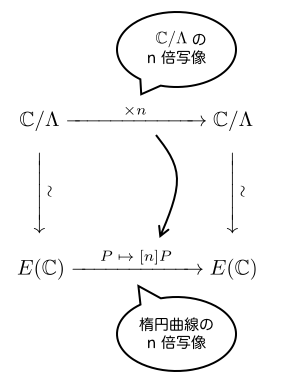
注意したいのは、今考えている写像が単に「複素数平面での 倍写像」ではなく「格子で割った平面の
倍写像」であるということです。つまり、
に対する
倍は
ということですが、 が
の元であることを確認する必要があります。実際、
が成り立てば上の式は
となるので、写像
がうまく定義されます(well-defined)。
事実、整数 に対して
は成立します。図で表すとこういうことです。格子の点は整数倍しても元の格子に入るのです。
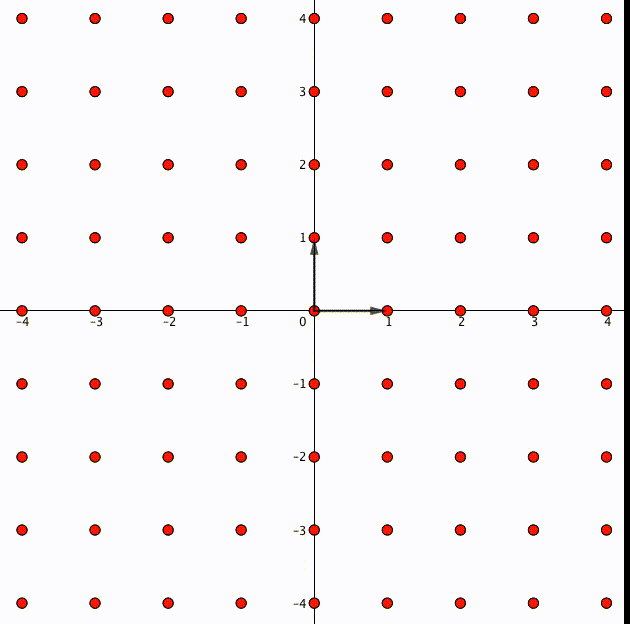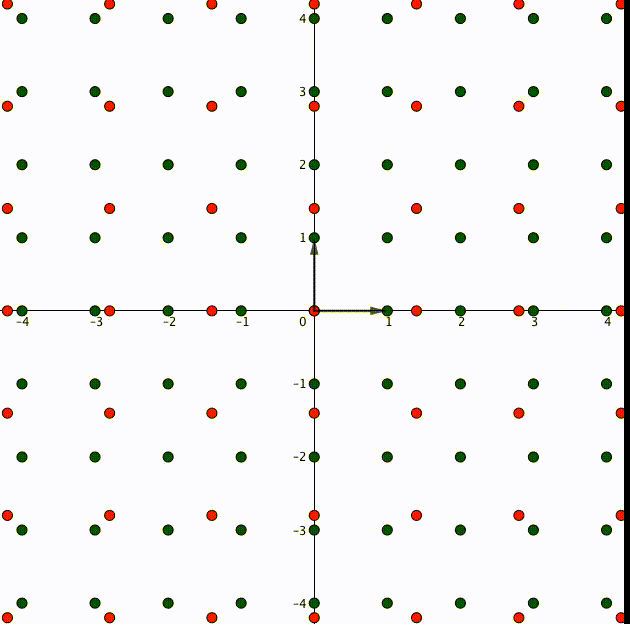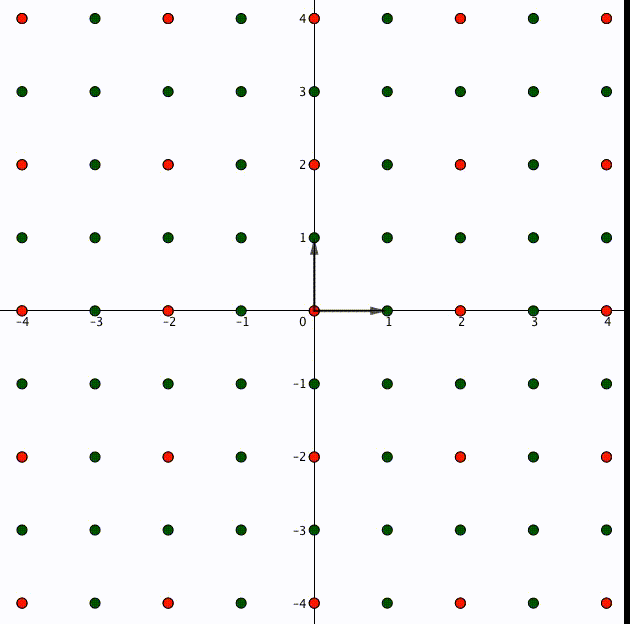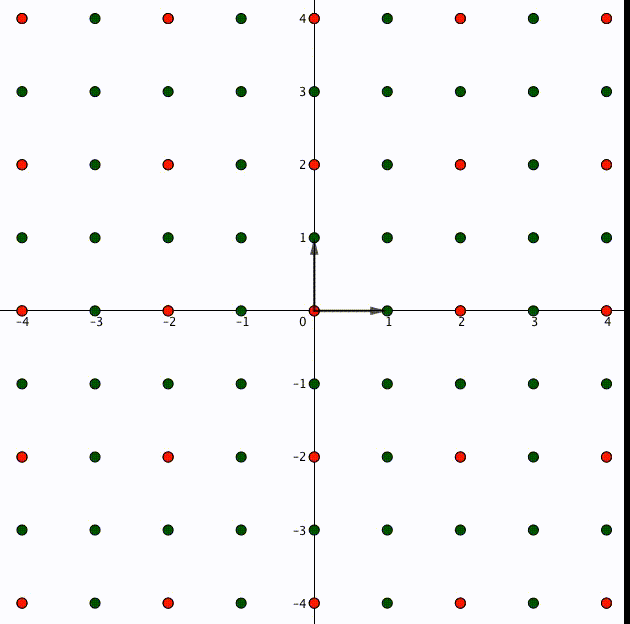
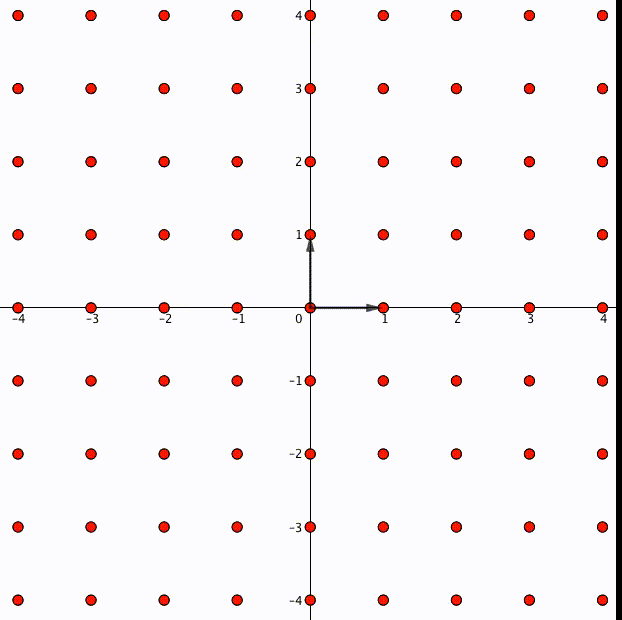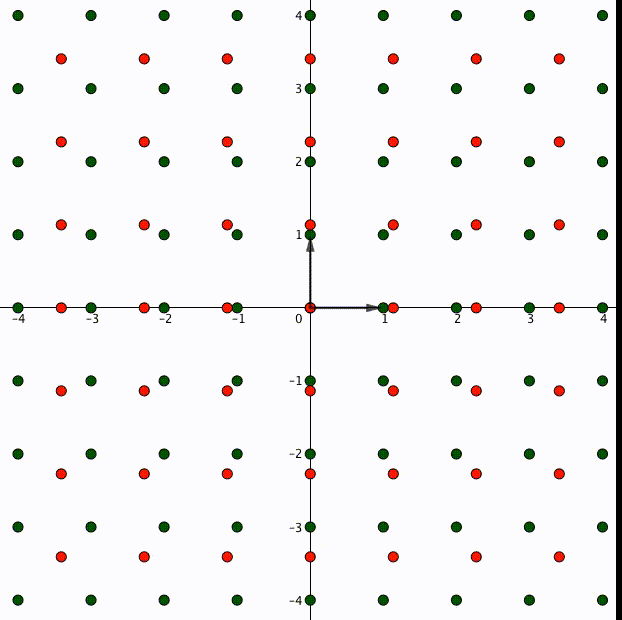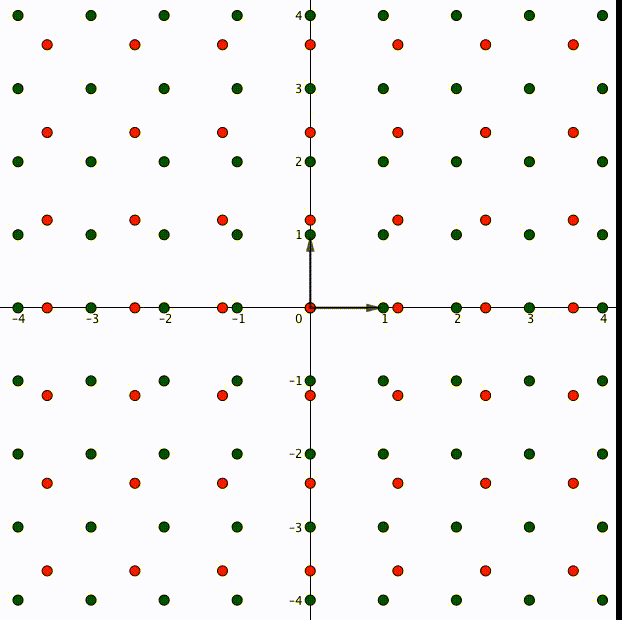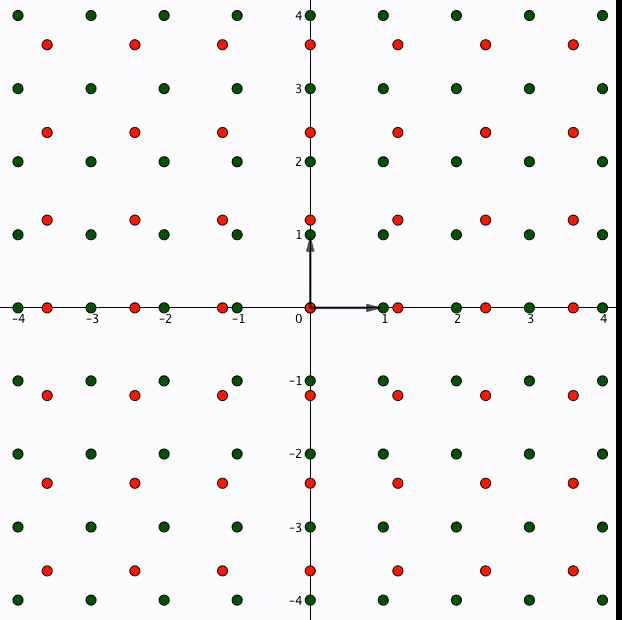
これがもし、整数ではない実数 であった場合、
は一般に成り立たないので
倍が適切に定義できません。たとえばこんな風に格子が元の位置からずれてしまいます。
「虚数」「乗法」
先ほどは、複素数平面での整数倍(あるいは実数倍)を考えました。今度は 複素数倍 を考えてみましょう。 として、
に対して
倍写像
を考えるのです。
実数倍のときに観察したように、 倍を定義するためには、格子に対して次の条件
を満たす必要があります。 式を満たすとき、
は自己準同型写像となります。これを「
倍写像」と呼びましょう。
以下は のときの
倍写像の例です。
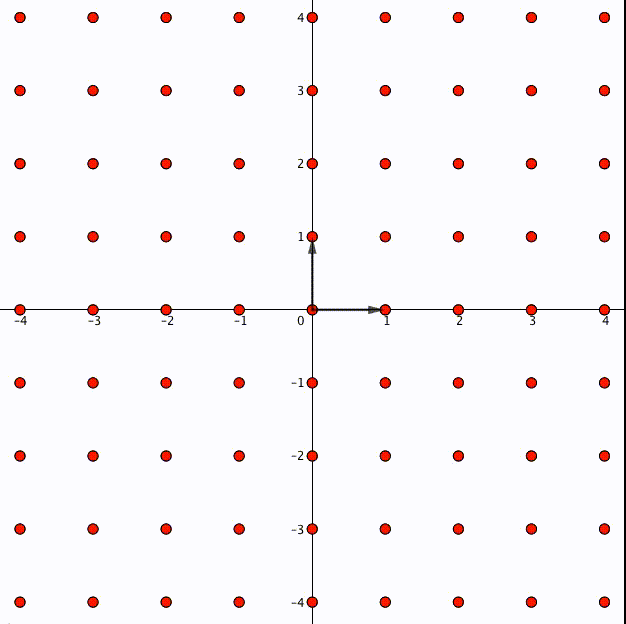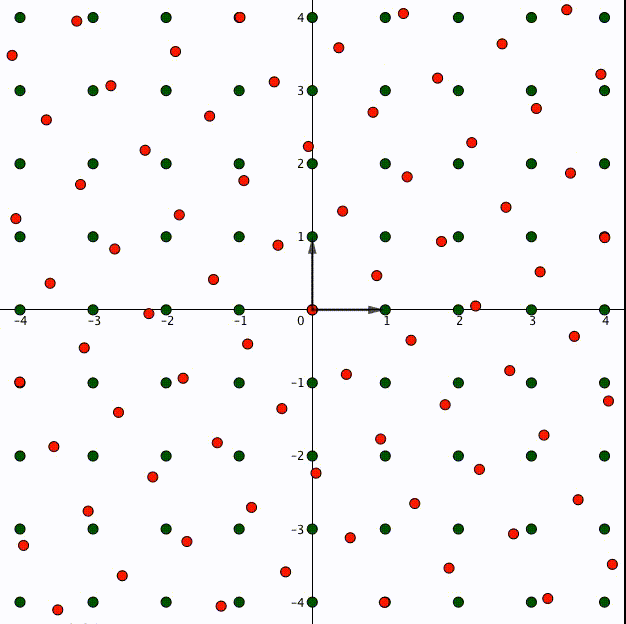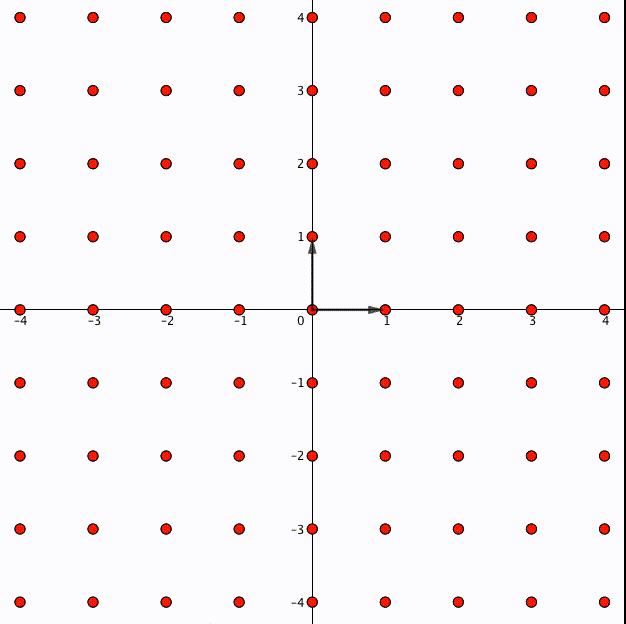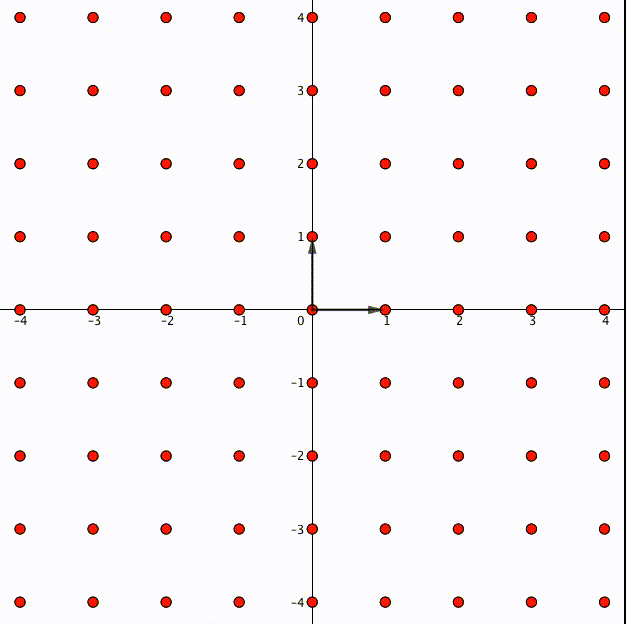
今定義した 倍写像を、解析的同型写像を通して楕円曲線側に移しましょう。楕円曲線上の点
の座標を
としたとき、
を以下のように定義します:
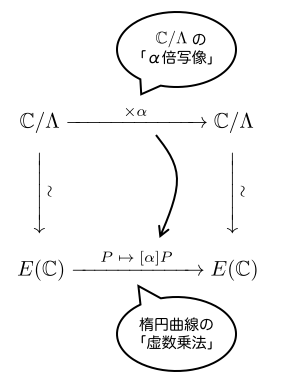
解析側の 倍写像
は、(解析的同型写像を通して)楕円曲線
の自己準同型写像
となります。そして、整数ではない
に対応する自己準同型写像は、「楕円曲線
における虚数乗法」となります。
つまり、解析側の「虚数(整数ではない複素数)の乗法」が、代数側における「虚数乗法」になっていたというわけです。これこそが、「虚数」「乗法」という呼び名の所以です。
それでは、虚数乗法の例を計算してみましょう。
楕円曲線の格子をガウス整数環 とします。この格子の周期は
であり
を満たします。したがって、 は
倍写像、すなわち虚数乗法を持ちます。この
倍写像が、解析的同型写像を通して楕円曲線における
という自己準同型写像に対応していることを確認しましょう。
解析側と代数側の対応を考えるために、ワイエルシュトラスのペー関数 とその微分
を計算しましょう。結果を述べると
となります。両辺を で微分すると(いつもの置換微分の公式を使うと)
が得られます。
したがって の定義より
となります。
たしかに、 における
倍写像が、
における
に対応することがわかりましたね。
このとおり解析側と代数側の対応を得るためには、式 のようにペー関数の「
倍公式」を経由する必要があります。三角関数のようにペー関数を使いこなせるようにならないといけません。
ここで、 なので、総和記号の中身を
と置き換えてよいから
式変形においては、 が本質的ですね。
自己準同型環と虚2次体
の自己準同型全体について考えてみましょう。
倍写像が、
の自己準同型となる条件は、
でした。そこで
という集合が、いったいどのような集合となるかに関心が向くでしょう。なぜなら、 は可換環として、
に対応する楕円曲線
の自己準同型環
に同型となるからです。
が成り立ちます。さらに の元は、解析的同型写像を通して対応する楕円曲線
の自己準同型となります。解析的同型写像は
の群同型なので、
の自己準同型写像
は、
に対応する自己準同型写像で尽くされます。すなわち、次の同型が成り立ちます。
結果として
が得られるというわけです。
以上を踏まえて、虚数乗法論における最も基本的な定理を述べたいと思います。
- 整数環
- 虚2次体
の整環(integer order)
証明は AEC を参照してください *2 。整数環 になるか、虚2次体の整環となることがわかりました。この基本的な定理によって、虚数乗法と虚2次体が切っても切り離せない関係になります。
虚数乗法を持つためには、上の定理における が虚2次数になる必要がありますが、「ランダムに」
を与えた場合、
が虚2次数になる確率は 0 であるため、対応する楕円曲線が虚数乗法をもつ確率が 0 であるというわけです。
これが第1回の記事において説明した『楕円曲線ダーツがあったとして、目をつぶって投げると、確率 1 で虚数乗法を持たない楕円曲線に当たる』の意味するところです。
以降のブログ記事では、特に自己準同型環が虚2次体 の極大整環、すなわち整数環
に同型な場合に限定して議論を進めていきたいと思います。
正規化の話(少し難しくなります)
上ではペー関数を経由して計算しましたが、代数側だけの議論によっても、 が「2乗して
になる写像」であることは以下のように確認できます。
となります。これが実は 倍写像になっています。
これが 倍写像
となっていることの確認は、たとえばこの写像をまた2回合成することで恒等写像、すなわち「1倍写像」になっていることからわかります。
ほかにも、 として
となり、(まだちゃんと定義できていませんが)楕円曲線の加法から、これが無限遠点 になり、0倍写像となることで確認できます。
写像の合成は自己準同型環においては「積」の演算になるのでした。したがって、2乗して になるということです。
ところが、「2乗して になる写像」に対応する解析側の
倍写像は、
倍写像と
倍写像のどちらでもよさそうですね。このように、解析側の
倍写像を代数側の虚数乗法に対応させる写像には、実は任意性があるのです。
一方で、前節で述べたように、解析側の 倍写像を解析的同型写像によって写す方法をとれば、対応関係は一意に定まります。しかしながら、この対応を与えるにはペー関数の具体的な計算が伴い、これがなかなか大変です。なんとか楕円曲線上の議論だけで済ませることはできないでしょうか。
そこで役に立つのは 微分形式 です。少し難しい話になりますので、ここの議論についてはわからなくても大丈夫です。
格子 を固定し、
に対応する楕円曲線
を考えます。
は虚数乗法を持つとし、
を虚2次体として、
であるとします。
解析的同型写像
に対し、「引き戻し」と呼ばれる逆方向の写像
が誘導されます。 はそれぞれ対応する1次微分形式(1-形式)の
-ベクトル空間です。
の座標を
とし、
の座標を
とすると
という写像になります。 を
で微分すると
となり、両辺を で割ると
が得られます。左辺は の1-形式、右辺は
の1-形式です。これが引き戻し写像
における対応を与えます。
上の微分形式
を
とおいて、これを
の 不変微分 と呼びます。
ここで の誘導する引き戻し写像
を
に対して適用すると
となることがわかります。つまり、 を通して、楕円曲線上の自己準同型写像
が
において
倍に対応するとわかるわけです。
一方で、任意の同型写像
が与えられているとします。この が任意の
に対して
を満たすとき は正規化されていると言います。
楕円曲線 に対して、正規化されている
は一意に定まることが証明できます。したがって、
であることがわかります。すなわち、
が正規化されていることは、
が解析的同型写像を通して
の
倍写像と対応すること の必要十分条件となっています。
実際、先ほどの の例では
となり、 が「
における
倍写像」に対応するとわかります。
とすれば、任意の整数
に対して
と定義することで正規化された同型写像
が得られます。
となるので、 であることがわかります。これで
と
を区別することができました。
おわりに
今日は、これまで代数側で定義されていた虚数乗法を、解析側で議論するための方法について述べました。虚数乗法は、解析側においてはまさに「虚数」の「乗法」だったことがわかったかと思います。
また、解析側と代数側は、解析的同型写像によって対応づいているので、適材適所で使い分けることができます。解析側 によって議論することはとても便利なので、今回の議論は今後の基礎となるでしょう。
ちなみに、ここまでの話が楕円曲線概説(上)の「虚数乗法」章における119ページ目に相当します。虚数乗法の章は115ページからなので、たった 5ページ しか進んでいないことになります。
ずいぶんと先は長そうですが、シリーズ3回目にしてようやく虚数乗法らしい話が出てきました。実は今回の話は、私が虚数乗法を学び始めて最初に感動したポイントでした。今回紹介できて嬉しく思います。今後も楽しみです。
それでは、今日はこの辺で。