合同数問題と保型形式（タネルの定理の証明の概略）

先週の日曜に梅崎さんが主宰する「数学について話す会」というイベントが開催されてtsujimotterも参加してきました。

数学について話す会

数学について話す会は「参加者全員が自分の好きな話をする」という、他ではあまりないタイプのイベントでした。参加者の聞き手としてのレベルが高く、発表者が気持ち良く話せるイベントだったと思います。tsujimotterは、本記事のタイトルにあるような「合同数」についての話をしてきたのですが、とても楽しくお話することができました。ほかの方の発表内容も興味深いものばかりでした。企画してくださった梅崎さんに感謝です。

さて合同数問題は、ぱっと見は初等的な問題に見えるのですが、実のところとても奥が深い問題です。合同数を判定するための「タネルの定理」と呼ばれる結果が知られているのですが、そこではなんと「保型形式」が関係します。

今日はそのタネルの定理について、私の知っている限りで紹介したいと思います。もちろん難しい内容なので、私自身は実際のところはよくわかっていませんし、誤解もあるかもしれません。「タネルの定理を完全解説するぞ」という大それたことを言うつもりはありません。あくまでこの記事の目的は「定理の成り立つ仕組みを表面的に追いかけて、何となくわかった気になろう」というものです。

より詳しく理解したい方は参考文献のコブリッツの本を読むか、あるいはコブリッツで参照されている論文にアクセスされるとよいかと思います。

「数学について話す会」で使ったスライドもこちらに上がっていますので、今回の記事の補助資料としてお使いください：

合同数問題と保型形式 from Junpei Tsuji

www.slideshare.net

目次：

合同数問題

楕円曲線に帰着

保型形式との関連

ヴェイユの定理

志村写像

ワルズプルジェの結果・タネルの結果

具体的なの構成

まとめと参考文献

合同数問題

合同数についてはtsujimotterのブログでも触れたことはありましたが、今一度復習してみましょう。
tsujimotter.hatenablog.com

まず、合同数の定義は「すべての辺の長さが有理数であるような直角三角形の面積になる整数」のことです。図で表すとこんな感じです。

f:id:tsujimotter:20180924210627p:plain:w200

たとえば、6は合同数です。いつもの3:4:5の直角三角形を考えれば、その面積が6になることがすぐに確認できます。

f:id:tsujimotter:20180924210804p:plain:w200

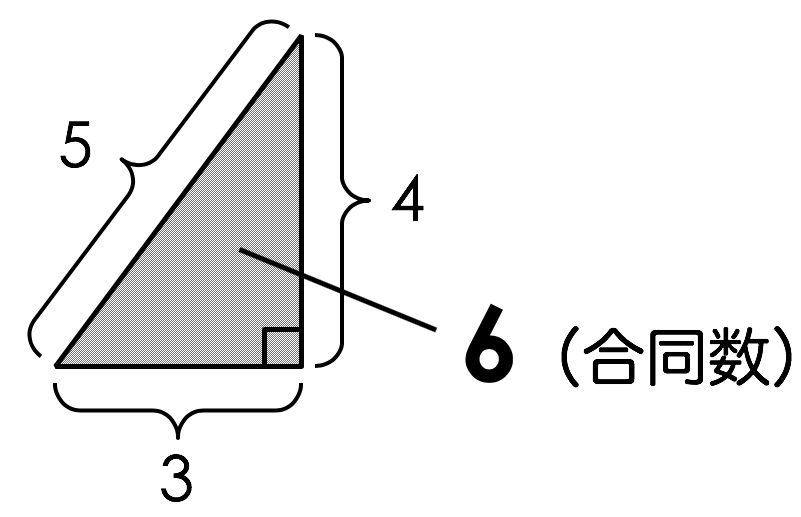
合同数とそうでない数の例を挙げておきましょう。

合同数の例：
5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, …
合同数ではない例：
1, 2, 3, 4, 8, 9, 10, 11, 12, 16, 17, 18, 19, 25, 26, 27, 32, 33, 35, 36, 40, 42, 43, 44, …

今、合同数の例をさらっと挙げましたが「与えられた数が合同数であること」や「合同数ではないこと」を示すのは難しい問題です。合同数ではないことを証明するためには、任意の直角三角形を考えてその面積と一致しないことを示さなければなりません。

たとえば、1が合同数でないことを示したのはフェルマーですが、その方法は無限降下法を必要とします。これ自体、なかなか面白い話なのですが、その話はまた今度。

さて、ある数が合同数であるかどうか判定する問題を合同数問題と呼ぶことにしましょう。今日のメインテーマであるタネルの定理は、合同数問題を（ある意味で）解決する定理です。

「え、それすごくないですか？」
「そう、すごいのです。」

では、タネルの定理を紹介しましょう。

定理（タネル, 1983）

$n$ を平方因子を持たない正の奇数とする．このとき， $(A)$ ならば $(B)$ が成り立つ．

$(A)\;\;$ $n$ は合同数．
$(B)\;\;$ $2x^2+y^2+8z^2=n$ を満たす整数の３つ組 $(x, y, z)$ の数は， $2x^2 + y^2 + 32z^2 = n$ を満たす整数の３つ組 $(x, y, z)$ の数の２倍に等しい．

また，弱バーチ−スウィナートン・ダイアー（Birch−Swinnerton-Dyer: BSD）予想が正しいとき， $(B)$ ならば $(A)$ が成り立つ．

いろいろ気になるところはあると思いますが、まずは定理の状況を整理しましょう。

まずこの定理は、合同数を判定する必要十分条件を与える定理になっているということです。つまり、

$(A) \;\; n$ は合同数 $\;\; \Longleftrightarrow \;\; (B)$ の条件が成り立つ

ということです。

ただし

$(A) \;\; n$ は合同数 $\;\; \Longrightarrow \;\; (B)$ の条件が成り立つ

は無条件で成り立ちますが

$(A) \;\; n$ は合同数 $\;\; \Longleftarrow \;\; (B)$ の条件が成り立つ

は弱BSD予想を仮定すれば成り立つというものです。

私たちが本当に知りたかったことは合同数の判定法ですから、 $\Longleftarrow$ が重要なのですが、こちらは「弱BSD予想が成り立てば・・・」という条件付きというわけですね。弱BSD予想はあとで述べるように有名な未解決問題なので、合同数の判定法は「完全には」解決してはいないということですね。

そうはいってもこのタネルの定理、なかなかすごい定理だと思います。実際に計算してみるとわかりますが、合同数の判定条件 $(B)$ はとても計算に向いている条件です。 $n$ が合同数かどうか判定するためには、 $n$ より $x^2, y^2, z^2$ が小さいような $(x, y, z)$ の組を全探索して、その個数を数え上げれば良いのです。このことは、実際にコンピュータでプログラムを書いてみると実感できると思います。

たとえば、こちらのブログでは100までの奇数について、タネルの定理を使って実際に合同数の判定をしています。
maxima.hatenablog.jp

ちなみに、今回の定理は「奇数」に限定していますが、偶数であっても同様の定理は成立します。今回は話の流れ上、割愛します。

タネルの定理を観察すると、疑問が２つ浮かびます。１つは、タネルの定理ではなぜ弱BSD予想が出てくるのか、という疑問です。もう一つの疑問は、条件 $(B)$ で出てきた $2x^2 + y^2 + 32z^2, \; 2x^2 + y^2 + 8z^2$ という2次形式は、いったいどこから現れたのかということです。一つ目の疑問は次の節で、二つ目の疑問はこの記事の最後で解決することでしょう。

楕円曲線に帰着

さて、合同数問題をどのようにしてタネルの定理に帰着させるのでしょうか。その最初の鍵になるのは楕円曲線です。

合同数の定義は、次のように定式化することができるでしょう。

$n$ が合同数であるとは

$\begin{cases} X^2 + Y^2 = Z^2 \\ \cfrac{XY}{2} = n \end{cases} \tag{1}$

を満たす $X, Y, Z \in \mathbb{Q}$ が存在するということである。

$X^2 + Y^2 = Z^2$ はピタゴラスの定理によって直角三角形になるという条件で、もう一つは $n$ がその直角三角形の面積になるという条件ですね。まずはここからスタートします。

以上の式は、適当な変数変換を施すことで楕円曲線の方程式に帰着することができるのです。すなわち、 $n$ が合同数であるときの $(X, Y, Z) \in \mathbb{Q}^3$ の組が存在するとき、次のように式変形できます。

f:id:tsujimotter:20180924213849p:plain:w600

簡単な式変形なので、目で追っていただければ理解できるかと思います。

さて、最後に得られた式は

$E_n : y^2 = x^3 - n^2 x \tag{2}$

という式ですが、これはまさに楕円曲線の定義方程式となっています。

とはいえ、これだけだと単に方程式の形を変えただけで、本質的には何も変わっていません。しかしながら、楕円曲線の形にすることにもメリットはあります。楕円曲線を解析する手法が使えるからです。

まず、先ほどの $(X, Y, Z) \mapsto (x, y) \in E_n$ の変数変換は、有理数の組を楕円曲線 $E_n$ の有理点に写しています。

逆に、楕円曲線 $E_n$ の有理点があったとして、合同数の条件を満たす直角三角形を作ることができるでしょうか。
その有理点がもし無限位数の点であれば、逆方向の変数変換 $(x, y) \mapsto (X, Y, Z)$ によって、合同数の条件を満たす $(X, Y, Z)$ の組が得られることがわかっています。

2018/09/30: 誤解がありましたので訂正しました。

$(x, y) \in E_n(\mathbb{Q})$ が $E_n$ の２倍点であり、かつ $y > 0$ であるとき、逆方向の変数変換 $(x, y) \mapsto (X, Y, Z)$ によって、合同数の条件を満たす $(X, Y, Z)$ の組が得られることがわかっています。

また、 $E_n(\mathbb{Q})$ のねじれ点（位数有限の点）全体の集合 $E_n(\mathbb{Q})_{\text{tors}}$ は

$E_n(\mathbb{Q})_{\text{tors}} = \{ \infty, (0, 0), (\pm n, 0)\}$

であることが具体的に確かめられます。したがって、位数有限の点には合同数の条件を満たす直角三角形に対応する点はありません。

上記の事実を示すためには、実際なかなか大変な議論が必要になるのですが、ここでは割愛します。コブリッツの第１章の多くはこの事実の証明に費やされています。

楕円曲線の有理点は有限生成アーベル群なので

$E_n (\mathbb{Q})\simeq \mathbb{Z}^r \oplus E_n(\mathbb{Q})_{\text{tors}}$

という表示を持ちます。ここで $r$ を $E_n (\mathbb{Q})$ のランクといい、 $\operatorname{rank} E_n (\mathbb{Q})$ と表します。

$E_n (\mathbb{Q})$ が無限位数の点を持つとき、 $r > 0$ なので、 $\operatorname{rank} E_n (\mathbb{Q}) > 0$ となります。したがって、合同数の条件は $E_n$ を用いて次のように表せるでしょう。

$n \; \text{は合同数} \;\; \Longleftrightarrow \;\; \operatorname{rank} E_n (\mathbb{Q}) > 0 \tag{3}$

あとは、このランクが正になる条件がわかれば合同数問題が解決するわけです。「楕円曲線のランクが楕円曲線のL関数の特殊値を使って表せる」というのが、何を隠そう BSD予想なのです。

予想（弱BSD）

$\operatorname{rank} E_n (\mathbb{Q}) > 0 \;\; \Longleftrightarrow \;\; L(E_n, 1) = 0 \tag{4}$

これが成り立つと仮定すれば、楕円曲線 $E_n$ のL関数 $L(E_n, s)$ の $s = 1$ における特殊値 $L(E_n, 1)$ の値によって、合同数の判定ができるというわけです。これは使えそうです。

なお、弱BSD予想は有名な未解決問題ですが、部分的には解決しています。楕円曲線が虚数乗法を持つ場合、コーツ・ワイルズの定理によって $\Longrightarrow$ が従います。 $E_n$ は都合よく虚数乗法を持つことが知られていて*1、したがって $\Longrightarrow$ は無条件で従うというわけですね。

コーツ・ワイルズの定理については、次の記事で解説したことがありました：
tsujimotter.hatenablog.com

なお、虚数乗法を持たないケースについてはKolyvaginや加藤和也先生が独立な方法で解決していて、虚数乗法を持つ持たないに限らず $\Longrightarrow$ は言えるようです。以下参考資料：
http://www.math.sci.osaka-u.ac.jp/~ochiai/wiles05.pdf

さて、これまでの道のりを一旦まとめましょう。

f:id:tsujimotter:20180924221619p:plain:w320

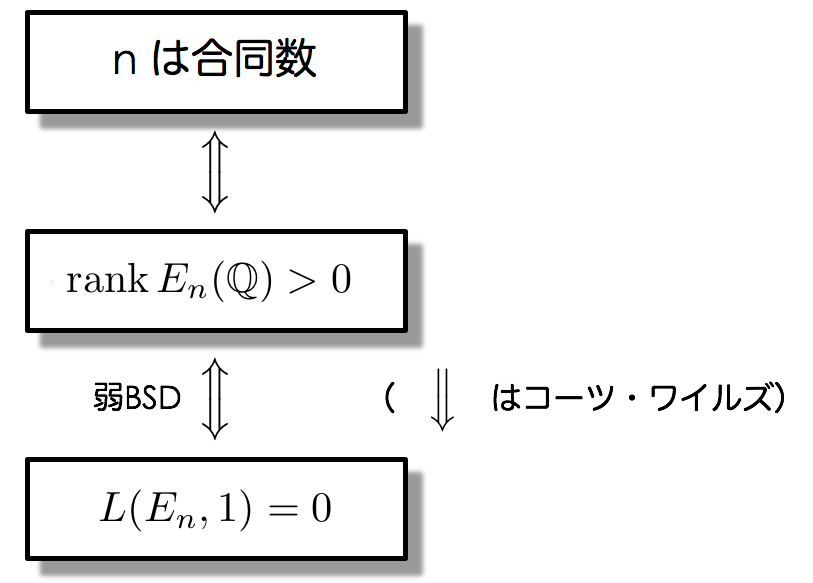
以上から、我々の目標は $L(E_n, 1) = 0$ になる条件を見つけるということになりました。

本節の最後に、楕円曲線のL関数について少し言及しておきましょう。L関数の定義についてはここで説明するつもりはありませんが、楕円曲線のL関数はディリクレ級数の形で表すことができるということについては触れておきたいと思います。

$n = 1$ のときの楕円曲線 $E_1$ は $y^2 = x^3 - x$ となりますが、あとで使うのでそのL関数のディリクレ級数を次のように表しておきましょう。

$\displaystyle L(E_1, s) = \sum_{m = 1}^{\infty}\frac{b_m}{m^s} \tag{5}$

以降、 $b_m$ といったら $E_1$ のL関数のディリクレ級数に出てきた係数の数列だと思うことにします。

また、一般の $E_n$ については $b_m$ を用いて次のように表すことができます。

$\displaystyle L(E_n, s) = \sum_{m = 1}^{\infty}\frac{\chi_n(m)b_m}{m^s} \tag{6}$

ただし、 $\chi_n$ は2次体 $\mathbb{Q}(\sqrt{n})$ に付随する2次指標と呼ばれるものです。詳しくはコブリッツの2.5節を参照してください。

ディリクレ級数の各係数に指標の値をかけることを「ツイスト」といいますが、 $L(E_n, s)$ は $L(E_1, s)$ の $\chi_n$ によるツイストになっているということですね。

保型形式との関連

ここまでは合同数と楕円曲線の関係について述べてきました。ここから先は、いよいよ保型形式が登場します。

まず、キーポイントについて先にリストアップしておきましょう。次の３つの結果が、タネルの定理証明の基本的なアイデアとなります。

ヴェイユの定理
志村写像
ワルズプルジェ（Waldspurger）の結果、タネルの結果

順番に説明していきましょう。

ヴェイユの定理

楕円曲線と保型形式の接点となる定理です。

リーマンゼータ関数の関数等式の証明を思い出してみましょう。あの証明では、テータ関数というある種の保型形式を考えて、そのメリン変換という積分を計算します。すると、ゼータ関数が得られます。一方で、テータ関数の保型性による変換を施した上でメリン変換すると、ゼータ関数の別の場所の値が得られます。両者を等式で結んで関数等式が得られるわけです。

同様に、「よい保型性」を持つ保型形式 $f$ に対してメリン変換を行うと、 $f$ に付随するディリクレ級数が得られて、その級数が複素数全体に解析接続されます。この関数を $f$ に付随するL関数ということにすると、このL関数が同様に関数等式を持つことが示せます。

ここで考えたいのは、この「逆」です。つまり、（都合のよい）関数等式を持つディリクレ級数が与えられたときに、逆メリン変換を施すことで保型形式を得ることができるか、という問題です。

実は、この問題には解答が得られていて、答えは「イエス」です。それがヴェイユの定理です。

f:id:tsujimotter:20180924224138p:plain:w400

詳細のステートメントは、やはりコブリッツの3.3節を読んでいただくとして、とにかくこんなすごいことが成り立つというのです。

これを合同数問題に応用しましょう。我々が関心があるのは、 $L(E_n, s)$ というディリクレ級数でした。この $L(E_n, s)$ は関数等式を持つことが示せます。したがって、ヴェイユの定理により、ある保型形式 $g_{E_n}$ が存在して、それが逆メリン変換によって $L(E_n, s)$ に対応します。

実際、 $L(E_n, s)$ に対応する保形形式 $g_{E_n}$ は、ウェイト $2$ でレベルが $\Gamma_0(32n^2)$ のカスプ形式になることが知られています。

これで問題が保型形式に持ち込まれました。

志村写像

続いて、保型形式の間のウェイトやレベルを超えた非自明な写像について述べます。

この定理はステートメントがとても難しく、ここでは正確に述べられません。おおざっぱに紹介しますが、次のような「志村写像」と呼ばれる写像が存在します。

f:id:tsujimotter:20180924225201p:plain:w500

保型形式の空間はベクトル空間になることがわかりますが、志村写像はベクトル空間の間の写像になっています。左側は、ウェイト $k/2$ でレベルが $N$ の保型形式の空間です。レベル $k/2$ というのは、 $k$ が奇数のときには、半整数になります。このような保型形式を半整数ウェイトの保型形式といいます。半整数ウェイトの保型形式は、コブリッツの第4章のテーマとなるトピックですが、通常の保型形式よりもやや難しくなります。 $\tilde{\Gamma}_0(N)$ は、保型因子付きの変換を表すのですが、この辺の記述がやや複雑になるようです。

要するに志村写像は、ウェイト $k/2$ （半整数）でレベル $N$ の保型形式を、ウェイト $k-1$ （整数）でレベル $N'$ の保型形式に移す写像ということになります。ここで $N'$ はNiwaの研究によって $N' = N/2$ と取れることが知られているそうです。

今回の問題で考えると、 $L(E_1, s)$ にヴェイユの定理によって対応する保型形式 $g_{E_1}$ は、右側の空間に入ります。これがウェイト $2$ 、レベル $32$ のカスプ形式になるというわけですが、この $g_{E_1}$ に対応するような左側の半整数ウェイトの保型形式はいったいなんだろうか、ということが知りたいわけです。

これについては、タネルによる計算によって、ウェイト $3/2$ 、レベル $128$ のカスプ形式 $f = \sum a_m q^m$ に対応することが示されています。

あれ？と思ったあなたの感覚は正しい。ついさっき「Niwaの研究によって $N' = N/2$ と取れることが知られている」と言ったばかりです。 $N' = 32$ ならば $N = 2N' = 64$ じゃないのかと思うのも当然です。

しかしながら、 $N$ に対して $N' = N/2$ ととれるという話は、左から右への矢印の場合です。逆は必ずしも成り立たない。つまり、レベル $N = 128$ の（左側の）保型形式に対して、 $N' = 64$ の（右側の）保型形式が対応するのは左から右の方向なので正しい。少し考えればわかるように、レベル32の保型形式はレベル64の保型形式でもあるわけです。したがって、 $N' = 32$ の（右側の）保型形式が $N = 128$ の（左側の）保型形式に対応していてもいいわけですね。

ややこしいですが、こんな感じです。この辺の事情はコブリッツの4.4節でも議論されています。

ワルズプルジェの結果・タネルの結果

最後のキーアイデアです。ヴェイユの定理と志村写像で、楕円曲線の問題を半整数ウェイトの保型形式まで引っ張り込んできました。保型形式を用いて、具体的に $L(E_n, 1)$ の値を与えるための結果を紹介します。

ワルズプルジェの定理は、非常に一般的な定理だそうなのですが、簡単にいうと次のようなことを主張しています *2。

ウェイト $k–1$ の保型形式のL関数の臨界値が，（志村写像で）対応するウェイト $k/2$ の保型形式の $q$ -係数の2乗で表せる．

臨界値というのは、関数等式で折り返した「折り目の部分」の値のことです。 $L(E_n, s)$ には $L(E_n, s) \leftrightarrow L(E_n, 2-s)$ という関数等式が成り立ちますが、折り目の部分は $s = 1$ です。我々が関心があるのも $L(E_n, 1)$ の値でした。これが、先ほどの志村写像で対応する半整数ウェイトの保形形式の $q$ -係数（の2乗）で表されるというのです。

このワルズプルジェの結果をもとに、 $E_n$ に対して具体的に計算したのが次のタネルの結果です。

定理（タネル，1983）

保型形式 $f = \sum a_m q^m \in S_{3/2}(\tilde{\Gamma}_0(128))$ で $\operatorname{Shimura}(f) = g_{E_1} = \sum b_m q^m$ かつ，平方数を持たない奇数 $n$ に対し

$\displaystyle L(E_n, 1) = \frac{\beta}{4\sqrt{n}}a_n^2 \tag{7}$

を満たすものが存在する

この結果によって、我々が求めたかった $L(E_n, 1)$ の値をその $q$ -展開の係数で計算できるような、半整数ウェイトの保型形式の存在が示されました。

$\beta$ は楕円曲線の周期と呼ばれる数で、0ではない値をとります。したがって、上の式からただちにわかるように

$L(E_n, 1) = 0 \;\; \Longleftrightarrow \;\; a_n = 0 \tag{8}$

が成り立ちます。

あとは、この $a_n$ の元となる半整数ウェイトの保型形式 $f$ を具体的に決定することができれば、合同数の判定法が得られます。

あと一息です。いよいよ、合同数問題のタネルの判定法を導きましょう。

具体的な $f$ の構成

もちろん、 $f$ はタネルによって具体的に構成されています。使う道具はテータ関数です。

テータ関数は、次の式で定義される関数です。

$\displaystyle \Theta(z) := \sum_{n \in \mathbb{Z}} q^{n^2} \tag{9}$

ただし、 $q = e^{2\pi i z}$ とします。このとき $\Theta(z)$ はウェイト $1/2$ の保型形式になります。テータ関数の保型性についてはコブリッツの3.3節で示されています。

さて、この $\Theta(z)$ を使うと、我々が欲しかったウェイト $3/2$ の保型形式 $f$ が次のように構成されます。

$\displaystyle f(z) = (\Theta(z) - \Theta(4z))(\Theta(32z) - \frac{1}{2}\Theta(8z))\Theta(2z) \; \in \; S_{3/2}(\tilde{\Gamma}_0(128)) \tag{10}$

ウェイト $3/2$ であることは簡単に示せます。上の式は、テータ関数3つの積の形で表されています。1つのテータ関数はウェイト1/2ですから、保型形式の積に対して「ウェイトが和になる法則」を使って、ウェイトが $1/2 + 1/2 + 1/2 = 3/2$ となります。

この $f$ を展開していきましょう。
$\displaystyle \begin{align} f(z) &= (\Theta(z) - \Theta(4z))(\Theta(32z) - \frac{1}{2}\Theta(8z))\Theta(2z) \\ &= \Theta(z) \Theta(32z) \Theta(2z) - \frac{1}{2}\Theta(z) \Theta(8z) \Theta(2z) - \Theta(4z) \Theta(32z) \Theta(2z) + \frac{1}{2}\Theta(4z) \Theta(8z) \Theta(2z) \end{align}$

これにテータ関数の定義式を代入すると

$\displaystyle \left(\sum_{x \in \mathbb{Z}} q^{x^2}\right)\left(\sum_{y \in \mathbb{Z}} q^{y^2}\right)\left(\sum_{z \in \mathbb{Z}} q^{z^2}\right) = \sum_{(x, y, z) \in \mathbb{Z}^3} q^{x^2 + y^2 + z^2}$

のような式が成り立つことから

$\displaystyle \begin{align} f(z) &= \sum_{(x, y, z) \in \mathbb{Z}^3} q^{2x^2 + y^2 + 32z^2} - \frac{1}{2}\sum_{(x, y, z) \in \mathbb{Z}^3} q^{2x^2 + y^2 + 8z^2} \\ &- \sum_{(x, y, z) \in \mathbb{Z}^3} q^{2x^2 + 4y^2 + 32z^2} + \frac{1}{2}\sum_{(x, y, z) \in \mathbb{Z}^3} q^{2x^2 + 4y^2 + 8z^2} \end{align}$

という式が得られます。

我々が知りたかったのは、 $f$ の $n$ 番目の $q$ -係数 $a_n$ でした。すなわち、上の式を同類項にまとめて $q^n$ の項の係数を知りたいわけですね。これについては、 $q^n$ となるようなパターンの個数を数えれば良いので、次の式が成り立ちます。

$\displaystyle \begin{align} a_n &= \# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 32z^2 = n\} \\ &- \frac{1}{2}\# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 8z^2 = n\} \\ &- \# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + 4y^2 + 32z^2 = n\} \\ &- \frac{1}{2} \# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + 4y^2 + 8z^2 = n\} \end{align}$

このようなテータ関数の解釈は、ヤコビの２平方定理の証明を思い出しますね。こんな風に「2次形式の個数」の問題に帰着できるというのが、テータ関数の真骨頂だと思います。

最後の仕上げです。後半の2つの2次形式

$\begin{align} 2x^2 + 4y^2 + 32z^2 = n, \\ 2x^2 + 4y^2 + 8z^2 = n \end{align}$

の左辺は、係数がすべて偶数なので偶数しか生成しません。一方、今考えている $n$ は奇数なので、このような条件を満たす $x, y, z$ の組は存在しません。したがって、個数は 0 になります。よって

$\displaystyle \begin{align} a_n = & \# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 32z^2 = n\} \\ &- \frac{1}{2}\# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 8z^2 = n\} \end{align}$

が成り立ちます。

ここで、合同数の条件は $a_n = 0$ だったことを思い出すと

$\displaystyle \begin{align} a_n = 0 \; \; \Longleftrightarrow \;\; & \# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 32z^2 = n\} \\ &= \frac{1}{2}\# \{ (x, y, z) \in \mathbb{Z}^3 \mid 2x^2 + y^2 + 8z^2 = n\} \end{align}$

得られます。

ついにやりました！これで冒頭で紹介したタネルの判定法に出てきた条件 $(B)$ が得られましたね！！

なるほどこういうことだったのか！！

まとめと参考文献

今日は、合同数の判定法である「タネルの定理」を紹介しました。

タネルの定理を導く道のりは、とても長いものでした。再度まとめましょう。私たちは次のような道のりを歩んできたことになります。

f:id:tsujimotter:20180925002018p:plain:w400

タネルの定理の条件を見て、最初はなんじゃこりゃと思ったかもしれませんが、こうして証明の概略を俯瞰してみるとなかなか納得できるものだったのではないでしょうか。

特に弱BSDを仮定する部分については、楕円曲線のランクとL関数を結びつける部分で使いました。謎の2次形式については、志村写像の逆像によって半整数ウェイトの保型形式に結びつけた後で、テータ関数の計算によって出てきたものでした。

最後に、今回大変お世話になった参考文献を紹介します。

N. コブリッツ「楕円曲線と保型形式」

楕円曲線と保型形式

作者: N.コブリッツ,上田勝
出版社/メーカー: 丸善出版
発売日: 2012/07/17
メディア: 単行本
購入: 1人クリック: 1回
この商品を含むブログを見る

今回の内容は基本的にこの本の内容に則っています。もちろん理解しきれていないところも多々ありますし、勘違いしている部分もあるかと思います。今回の記事で興味を持ってくださった方は、ぜひコブリッツの本にも挑戦してみてください。私もこれから頑張って勉強します。

最後に、今回の内容をまとめるに当たって気づいたことを述べて終わりにします。

コブリッツの各章は
2章　楕円曲線とハッセ-ヴェイユL関数
3章　保型形式
4章　半整数ウェイトの保型形式

と並んでいますが、よくよく考えてみると、すべての章のトピックがタネルの定理の証明に登場しますね。

私はこのコブリッツの本を「保型形式」を勉強するために買ったのですが、実際のところ読んだことがあるのは３章だけでした。２章は楕円曲線なのでシルバーマンの本で勉強すればいいと思っていたし、４章はやけに難しいので食わず嫌いしていたのです。

しかしながら、合同数のことを知ってから読んでみると、コブリッツの主役は実は合同数だったのです。そのことはイントロにも書いてあります。そして事あるごとに合同数に関係する $E_n$ の計算が登場し、最終的にタネルの定理の証明の概略を述べて終わるわけです。半整数ウェイトの保型形式も重要な役割を果たします。

コブリッツのメインストーリーは合同数であったのにもかかわらず、結果的には楕円曲線や保型形式のことを網羅する教科書にもなってしまっている。これは、合同数の奥深さを物語っていますね。

今回の勉強をきっかけに、合同数は実のところ数論の「王道」だったのだということに気づきました。tsujimotterは合同数のことが大好きになりました。

それでは今日はこの辺で。

*1: $E_n : y^2 = x^3 - n^2x$ は $(x, y) \mapsto (-x, \sqrt{-1})$ という $N \in \mathbb{Z}$ 倍写像ではない自己準同型を持ちます。