曲線と関数体 (2)：楕円曲線の加法はなぜ「あの」定義なのか？

今回のテーマは

楕円曲線の加法はなぜあの定義なのか？

です。前回に引き続き、楕円曲線の謎に迫っていきましょう。

前回の記事はこちら：
tsujimotter.hatenablog.com

楕円曲線の加法とは

定義方程式

$E\colon Y^2 = X^3 + aX + b \tag{1}$

で与えられる楕円曲線 $E$ を考えます。

一般に $E$ の任意の２点 $P, Q$ が与えられたとき、 $P, Q$ の加法 $P + Q$ が定義できます。つまり、 $P + Q$ という点が $E$ の上に定まるわけですが、これは次のように幾何学的に決定されます。

$E$ の点 $P$ と $Q$ をとり、２点を通る直線と $E$ との交点を $R$ とします。つまり、 $P, Q, R$ が同一直線上に乗ります。

f:id:tsujimotter:20190703123803p:plain:w300

このことを、加法の記号 $+$ を用いて

$P + Q + R = O \tag{2}$

と表すことします。これが成り立つように、２点 $P, Q$ の間の加法を導入します。

ここで $O$ を $E$ の単位元とします。楕円曲線が式 $(1)$ の形で表されているときは、単位元 $O$ は無限遠点 $P_\infty$ とすることができます。

式 $(2)$ を加法の性質を満たすように変形すると

$P + Q = -R$

となり、これが $P + Q$ の定義となります。

$-R$ とは何でしょうか。逆元の性質 $R + (-R) = O$ と $O = P_\infty$ より

$R + (-R) + P_\infty = O \tag{3}$

となりますが、式 $(2)$ と同じように解釈すれば「 $R, (-R), P_\infty$ は同一直線上にある」ということです。すなわち、図に表すとこういうことです。

f:id:tsujimotter:20190703143843p:plain:w300

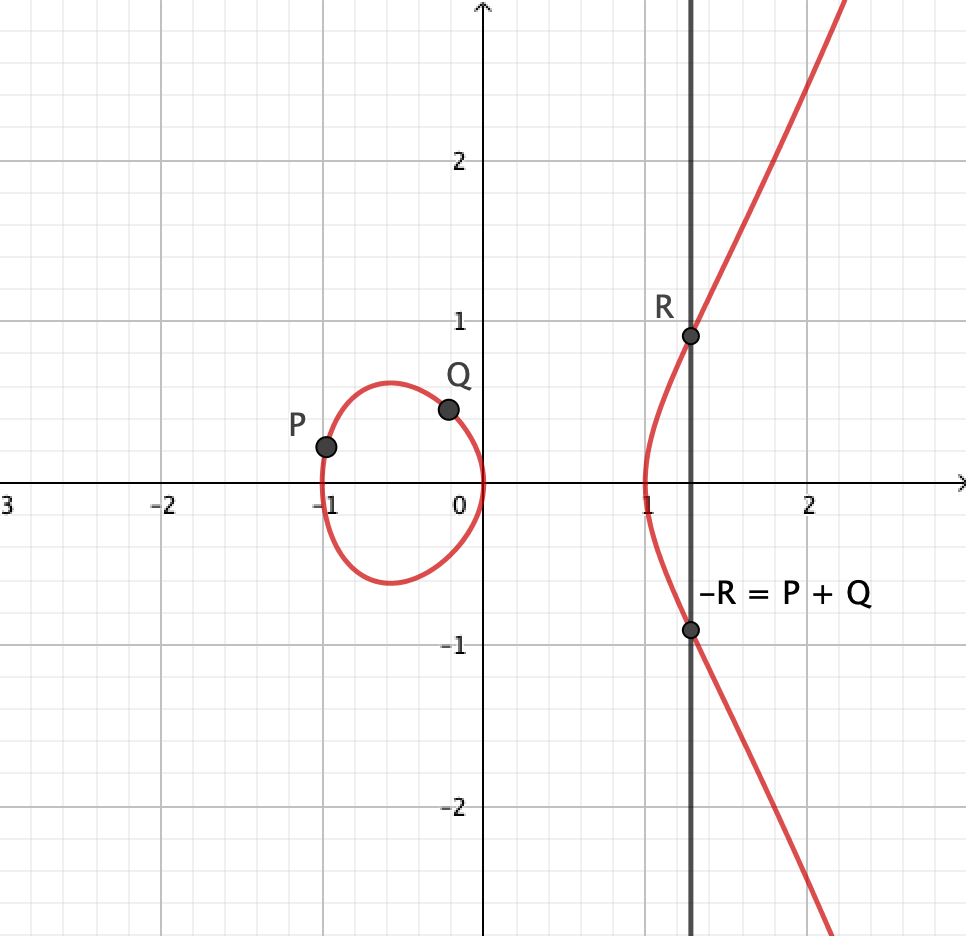
$R$ と $(-R)$ を結ぶ直線は $y$ 軸と並行で、一見 $E$ との交点を持たないように見えますが、実は無限遠点 $P_\infty$ と交わっている、と考えることができます。

以上の議論により、 $P + Q = -R$ として、楕円曲線の加法が幾何学的に計算できるようになりました。

ところでこの加法、なぜこんな風に定義されるのでしょうか。

$P + Q + R = O \;\; \overset{\text{def}}{\Longleftrightarrow} \; \; P, Q, R$ は同一直線上にある

という定義は、いったいどこからやってきたのでしょうか。

ここまでが導入です。今日は楕円曲線の加法が、とある代数的な演算によって「自然に」定義される仕組みを説明したいと思います。

キーになる概念は「因子」と「因子類群」です。

因子と因子類群

前回の記事では、楕円曲線 $E$ の関数体 $\mathbb{C}(E)$ を定義しました。関数体の元に対して、極や零点の位数を計算しましたね。

たとえば、関数 $X, Y$ の場合の極と零点の位数はこうでした。

関数 $X$ は $P_0$ で $2$ 位の零点を持ち、 $P_\infty$ で $2$ 位の極を持つ。
関数 $Y$ は $P_{-1}, P_0, P_1$ で $1$ 位の零点を持ち、 $P_\infty$ で $3$ 位の極を持つ。

上記をより簡潔に表す表現として、次の記法を考えましょう。

関数 $X$ については

$2P_0 - 2P_\infty$

関数 $Y$ については

$P_{-1} + P_{0} + P_{1} - 3P_\infty$

とします。

見たらわかると思いますが、零点や極を「和」の記号で並べて、その係数として零点や極の符号付きの位数が掛けられています。零点は正の係数、極は負の係数です。この和の記号はあくまで形式的な記号であって、特に点同士の和を計算しているわけではないことに注意してください。

一般の関数 $h\in \mathbb{C}(E)$ に対しても、極や零点に関して符号付きの位数をかけて足し合わせたものを考えます。このとき、極と零点は有限個なので、このような和は有限和になることに注意します。

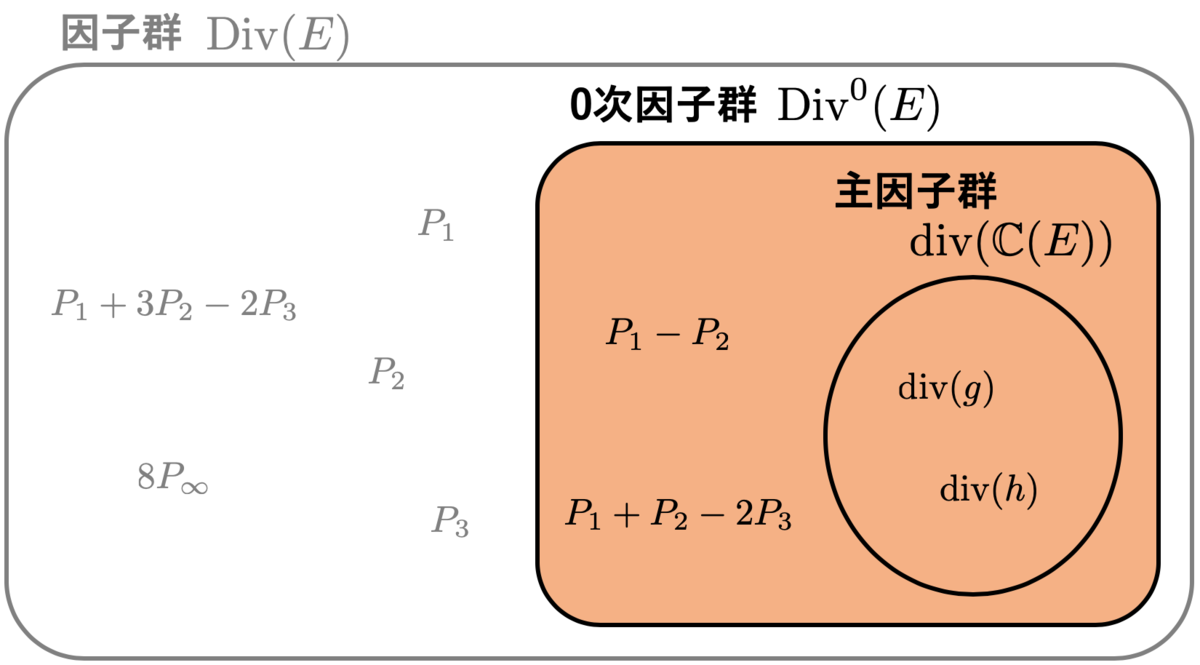
このように、曲線上の点 $P \in E$ に対して整数係数をかけて、有限個の形式的な和をとって表したものを因子（divisor）といいます。すなわち、因子は

$\displaystyle D = \sum_{P\colon \text{有限和}} m_P P$ （ただし、 $m_P \in \mathbb{Z}$ ）

の形で表せる形式的な和のことです。因子同士は、単純に係数を足し合わせる計算によって自然に加法を定義できます。

楕円曲線 $E$ の因子全体のなすアーベル群のことを $E$ の因子群と呼ぶことにして、 $\operatorname{Div}(E)$ と表しましょう。

また、任意の関数 $h \in \mathbb{C}(E)$ に対応する因子を $\operatorname{div}(h)$ と表すことにすると、

$\operatorname{div}( \mathbb{C}(E) ) := \{ \operatorname{div}(h) \mid h \in \mathbb{C}(E) \}$

は、因子群 $\operatorname{Div}(E)$ の部分群になります。これを主因子群といいます。

f:id:tsujimotter:20190703170731p:plain:w400

ここで、主因子群（関数全体に対応する因子）に対して、因子群がどの程度大きいかを表す指標を考えたくなります。それが因子類群です。

因子類群 $\operatorname{Cl}(E)$ は、因子群を主因子群で割ってできる群として定義されます。

$\operatorname{Cl}(E) := \operatorname{Div}(E)/\operatorname{div}( \mathbb{C}(E) )$

因子類群の加法は、 $\operatorname{div}( \mathbb{C}(E) )$ で割ったあまりによって自然に誘導されたものを考えます。

また、因子類群における単位元は $\operatorname{div}( \mathbb{C}(E) )$ になります。すなわち

$D \equiv 0 \pmod{\operatorname{div}( \mathbb{C}(E) )} \;\; \Longleftrightarrow \;\; D = \operatorname{div}(h)$ なる $h \in \mathbb{C}(E)$ が存在する

ということです。これはあとで使います。

これから考えたいことは、楕円曲線 $E$ をこの因子類群に写すことです。因子類群に写された加法を調べることで、楕円曲線の加法を定義しようというものです。

しかしながら、楕円曲線を写すには、因子類群はやや大きすぎます。もう少し小さいものを考えたくなります。

思い出していただきたいのは、関数における零点や極の位数です。前回の記事では、関数体の元について

（零点の位数の合計）＝（極の位数の合計）

なる関係が成り立つことを観察したかと思います。

ここで、因子 $D = \sum m_P P$ に対して次数という写像を導入しましょう。

$\displaystyle \operatorname{deg}(D) = \sum_{P} m_P$

すなわち、 $P$ に対する係数をを単純に足し合わせたものが次数の定義です。

このとき、 $h \in \mathbb{C}(E)$ に対して

$\operatorname{deg}(\operatorname{div}(h)) = 0$

が成り立つ、というのが上の観察でした。

そこで、因子群 $\operatorname{Div}(E)$ を考える代わりに、次数 $0$ の因子群 $\operatorname{Div}^0(E)$ を考えるというのは自然な発想でしょう。

$\operatorname{Div}^0(E) := \{ D \in \operatorname{Div}(E) \mid \operatorname{deg}(D) = 0 \}$

0 次の因子群に対して、同様に 0 次の因子類群 $\operatorname{Cl}^0(E)$ を考えます。

$\operatorname{Cl}^0(E) := \operatorname{Div}^0(E)/\operatorname{div}( \mathbb{C}(E) )$

これが今回のキーとなります。

f:id:tsujimotter:20190703170815p:plain:w400

楕円曲線と因子類群の関係

楕円曲線 $E$ を今定義した因子類群 $\operatorname{Cl}^0(E)$ に写すための方法を考えます。そのために、仲介となる集合 $D_g^{+}$ を考えます。

$D_g^{+} := \{ D \in \operatorname{Div}(E) \mid \operatorname{deg}(D) = g, \; D \, \text{は正因子} \}$

$g$ は曲線の種数であり、正因子とは任意の係数 $m_P$ が非負であること（0 も含む）を言います。すなわち、次数がちょうど $g$ で正因子であるもの全体の集合です。

ここで、我々が考えているのは、楕円曲線ですから種数は $g = 1$ です。この場合、次数 $1$ の正因子なので、要するに $E$ の点全体ですね。したがって

$E = D_1^{+}$

であるといえます。

次に、 $E$ の無限遠点を $P_\infty$ として、写像 $\phi$ を考えます：

$\begin{matrix} \phi \colon & D_1^{+} &\to & \operatorname{Cl}^0(E) \\ & P & \mapsto & P - P_\infty \pmod{\operatorname{div}( \mathbb{C}(E) )} \end{matrix}$

$P - P_\infty$ は次数 0 なので、その剰余類はちゃんと $\operatorname{Cl}^0(E)$ に入っていることに注意しましょう。

このとき、リーマン・ロッホの定理によって、 $\phi$ が全射かつ単射であることが示せます。すなわち、 $D_1^{+}$ と $\operatorname{Cl}^0(E)$ の間に全単射が存在するということです。

よって $E$ と $\operatorname{Cl}^0(E)$ の間の全単射が言えました。

楕円曲線の加法はなぜあの定義なのか？

それでは、楕円曲線 $E$ と因子類群 $\operatorname{Cl}^0(E)$ の間の全単射を通して、因子類群に成り立つ加法を楕円曲線に遺伝させることを考えましょう。

楕円曲線に因子類群の加法を遺伝させたときに、楕円曲線 $E$ の点 $P, Q, R$ の間に

$P + Q + R = O$

が成り立つとしましょう。この式は、因子類群側ではどのような情報を表しているのでしょうか。

$P, Q, R$ を $\phi$ によって $\operatorname{Cl}^0(E)$ に送ると

$(P - P_\infty) + (Q - P_\infty) + (R - P_\infty) \equiv 0 \pmod{\operatorname{div}( \mathbb{C}(E) )}$

となります。これはつまり

$P + Q + R - 3P_\infty \equiv 0 \pmod{\operatorname{div}( \mathbb{C}(E) )}$

ということです。

合同の定義により

$P + Q + R - 3P_\infty = \operatorname{div}(h)$

なる $h \in \mathbb{C}(E)$ が存在する、ということです。この関数 $h$ について考察しましょう。

左辺の因子を見ると、 $h$ は点 $P_\infty$ に位数 $3$ の極を持ちます。

ここで、前回計算した一般論を思い出しましょう。リーマン・ロッホにより、楕円曲線 $E$ の「点 $P_\infty$ で高々位数 $3$ を持つ関数のなすベクトル空間」は、次のように表せるのでした：

$L(3P_\infty) = \mathbb{C} + \mathbb{C}X + \mathbb{C}Y$

これを使いましょう。すなわち

$h \in L(3P_\infty) = \mathbb{C} + \mathbb{C}X + \mathbb{C}Y$

となるため

$h(X, Y) = a_0 + a_1 X + a_2 Y$ （ここで、 $a_0, a_1, a_2 \in \mathbb{C}$ ）

となります。これは要するに直線の方程式ですね！！

また、同じく因子を観察することで、点 $P, Q, R$ は $h$ の零点であるとわかります。したがって

$\begin{cases} h(P) = 0 \\ h(Q) = 0 \\ h(R) = 0 \end{cases}$

ということです。

よって、 $P, Q, R$ の $X, Y$ 座標を代入することで、次が成り立ちます。

$\begin{cases} a_0 + a_1 X(P) + a_2 Y(P) = 0 \\ a_0 + a_1 X(Q) + a_2 Y(Q) = 0 \\ a_0 + a_1 X(R) + a_2 Y(R) = 0 \end{cases}$

これは、 $P, Q, R$ が同一直線上にあることを表しています！！

以上により、楕円曲線の加法

$P + Q + R = 0$

が「 $P, Q, R$ が同一直線上にあること」を意味することがわかりました。

まとめ

楕円曲線の加法がなぜ

$P + Q + R = O \;\; \overset{\text{def}}{\Longleftrightarrow} \; \; P, Q, R$ は同一直線上にある

のような式で定義されるのか、という点について考えてきました。

今回のキーは、因子と因子類群でした。因子類群 $\operatorname{Cl}^0(E)$ を考えると、それが楕円曲線 $E$ との全単射を構成することができます。因子類群には、因子の間に自然な加法が定まるので、上の全単射によって楕円曲線に加法を遺伝させることができます。

このような方法で導入した楕円曲線の加法を考えると、同一直線上にある点 $P, Q, R$ に対して $P + Q + R = O$ が成り立つ、というのが今回の話の流れでした。

なぜ同一直線上なのかというと、２つ理由がありました。一つ目は、 $P, Q, R$ を零点に持つ関数 $h$ が存在してそれが $L(3P_\infty)$ に属するからで、二つ目は、 $L(3P_\infty)$ の基底がリーマン・ロッホにより $1, X, Y$ とかけるから、という理由でした。

今回導入された「因子類群」は、楕円曲線やより一般に代数曲線を分析する道具として基本的なものなのだそうです。これまではあまりイメージが沸かなかったのですが、一連の記事でまとめたことによって、ずいぶんと親しめたような気がします。

また、関数体のベクトル空間を決定するときや、最後の直線の方程式を出すところ、因子類群との全単射を示すところなど、要所でリーマン・ロッホの定理が活躍しました。少し前まで、リーマン・ロッホの定理という名前しか知らなかったので、重要な定理であることが理解できてよかったです。

「曲線と関数体」シリーズはこれでおしまいです。読んでくださったみなさまありがとうございました。

それでは今日はこの辺で。

謝辞

今回と前回の記事を書くことになったきっかけについて少し話します。

最近、参考文献の数論入門の第９章「超楕円曲線とヤコビ多様体」を読んでいました。この本は実は何度も目を通していて、読むたびに感動していました。しかしながら、数ヶ月すると内容を忘れてしまって、読んでは感動してまた忘れて、を繰り返していました。

この数学書、何度読んでも感動する
— tsujimotter (@tsujimotter) 2019年6月26日

今回こそは理解したぞという手応えがあったのですが、ブログに書くのは面倒だなと思っていたのです。そんなときに、みずすましさんという方が「聞いてみたい」と言ってくださったのです。そこで、日曜数学会というイベントでお話しすることにしました。

懇親会では、最近僕の中でホットな、因子と因子類群の話をしました！

最終的には「種数1の曲線の方程式がなぜ3次曲線でかけるのか」と
「楕円曲線の加法がなぜああ定義されるのか」を（30分ぐらいで？）解説しました。

聴いてくださった三好さん他３名の方ありがとうございます。 #日曜数学会 pic.twitter.com/JozydRPTrU
— tsujimotter (@tsujimotter) 2019年6月29日