次多項式
を考えるとき、方程式 の判別式とは、
個の解
を用いて
と表せる量のことです。
たとえば、3次方程式 を考えて、その3つの解を
とするとき
と表すことができますね。要するに、すべての解の差をとり、2乗して掛け合わせたものですね。
定義から明らかなように、 が重根を持つなら判別式は 0 となります。つまり、判別式は重根の存在の判定器になっているということですね。ほかにも判別式にはいろいろな面白いことがありますが、今日は深入りはしません。
さて、今日はこの3次方程式の判別式を計算したいと思います。
背景
tsujimotterの元々のモチベーションは3次方程式の解の公式の計算でした。その過程で、3次方程式の判別式を係数で表そうとしていました。
判別式 が方程式の係数を用いて表せることは次のようにわかります。
は3つの解の
のすべての置換に対して不変な量になります。したがって、対称式になるわけです。
また、対称式の基本定理により、 は基本対称式の有理式で表せます。
さらに解と係数の関係
が成り立つので、結局 は
を用いて表せるわけです。
ここで気になるのは、どうやって を用いた式で
を表せるかということです。
もちろん定義にしたがって を素朴に展開し、がんばって基本対称式を探して置き換えていく方法がとれますが、それはちょっと面倒ですね。
1つめの方法は、計算機に投げてしまう方法です。Wolfram Alphaというサイトで
symmetricreduction(((alpha - beta) (beta - gamma) (gamma - alpha))^2, {alpha, beta, gamma})
と打ち込んできてください。結果は以下で確認できます。
www.wolframalpha.com
そんなわけで、結果はわかりました。でも、できれば手計算で求めてみたい。
2つめの方法は、対称式に現れる単項式の指数の組に辞書式順序を入れて、単項式の次数を下げていく方法です。これは「ウェアリングの方法」と呼ばれるものだそうで、対称式の基本定理の証明でも用いられるようです。
3つめの方法は「終結式」を用いた方法です。今日はこれを使って計算してみたいと思います。
この方法は、Twitterでジオッコ・ピアノさんという方から教えていただきました。ありがとうございます。
終結式とは
終結式とは、2つの次数 の多項式
に対して定まる量 で、それぞれの多項式の係数を用いた次の行列式によって計算されるものです:
なんじゃこりゃと思うかもしれません。
まず、行列の空欄の部分は 0 だと思ってください。また、行列のサイズとしては、 次の正方行列となります。
係数がなんというか、斜めに並んでずれながら並んで行くのが特徴ですね。このなんともいえない定義は、あとで具体的に計算することで確かめることにしましょう。
さて、この終結式を用いると、次のようなことが成り立つというのです。
を
次方程式とし、その最高次の係数を
とします。また、
を
での微分としましょう。
の判別式を
とするとき、次が成り立ちます。
面白いですね。判別式が、謎の行列式によって表現されるというのです。
重要なことは、上の終結式 は、実質的に
の係数のみによって表せるということです。 解と係数の関係によって、
の係数は(
の根の)基本対称式そのものといえます。結局のところ、判別式を「基本対称式を係数とする行列式」で表せるということですね。
式 についての証明はやりませんが、今日は実際にこの方法を使って、3次方程式の判別式を計算してみましょう。
3次方程式の判別式の計算
とすると、
です。ここで、終結式は
となります。たしかに 次の正方行列になっていますね。
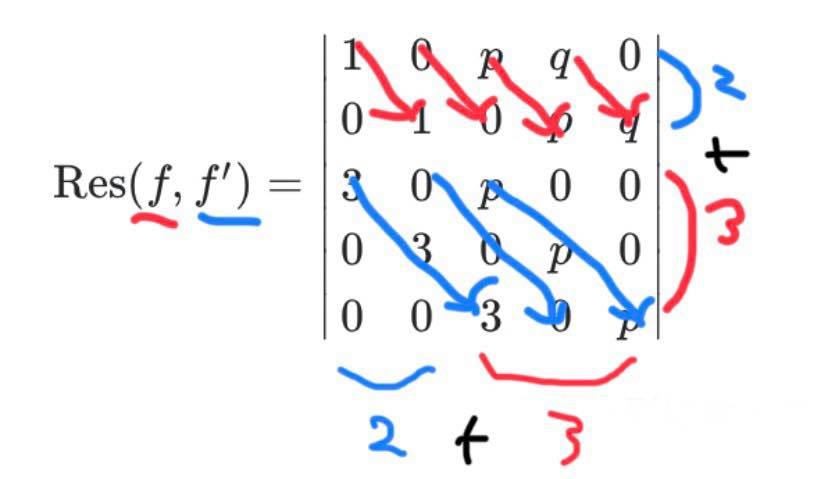
式 によると
が成り立つということでした。
この行列式を計算するために、余因子展開を計算しましょう。一番左の列の を使って展開します:
さらに、それぞれの行列式を同じように展開します。
最後に、3次の行列式をサラスの方法によって解くと
が得られます。
結局、終結式は
となります。
判別式と終結式の関係 により
と計算できました!やったー!!
それでは今日はこの辺で。
参考
終結式のイメージは、こちらのサイトの説明がとてもわかりやすいです。
mathtrain.jp
なお、私の記事では、都合上シルヴェスターの行列式で表されたものを終結式の定義としています。上の記事の方法によって終結式を定義した場合、「終結式はシルヴェスターの行列式で表される」は定理となります。