モジュラー曲線(3)：複素トーラスとしての楕円曲線

今回の記事は、楕円曲線についての基礎的な事項についてのおさらいです。

これまでのtsujimotterのノートブックでは、色々な記事で楕円曲線について紹介してきました。しかしながら、どれも文字数や手間の関係で駆け足で紹介せざるを得ませんでした。ここで一度腰を据えて丁寧に解説したいと思います。

楕円曲線は、代数曲線としての側面を紹介することが多いですが、今回は複素トーラスとしての側面について中心に紹介します。これは、後でモジュラー曲線に関する記事で使うことを想定しています。

モジュラー曲線関連の情報は、以下のタグの一連の記事でまとめているところです。
tsujimotter.hatenablog.com

なお、今回の記事はモジュラー曲線に関するシリーズ記事の一環で書いていますが、今回の記事に関して言えば、これまでの知識なしで読めるものとなっています。

目次：

1. 楕円曲線＝複素トーラス

2. 楕円曲線の射

3. 上半平面 H と楕円曲線

4. 楕円曲線のモジュライ空間

5. おわりに

補足：補題6の証明

参考文献

1. 楕円曲線＝複素トーラス

$\mathbb{C}$ の部分集合 $\Lambda$ を考えます。 $\Lambda \subset \mathbb{C}$ が次の２つを満たすとき、格子であるといいます。

$\omega_1, \omega_2 \in \mathbb{C}$ が存在して $\Lambda = \mathbb{Z}\omega_1 + \mathbb{Z}\omega_2$ と表せる
$\{\omega_1, \omega_2\}$ は $\mathbb{C}$ の $\mathbb{R}$ 上の基底である（つまり、 $\mathbb{C} = \mathbb{R}\omega_1 + \mathbb{R}\omega_2$ であるということ）

要するに、 $\mathbb{C}$ 上で規則的に広がった離散的な点集合のことですね。

以降、次のような記法を用います。

格子の基底が $\{\omega_1, \omega_2\}$ であることを明示するときは、 $\Lambda_{\omega_1, \omega_2}$ と表現します。
格子の基底が $\{ \tau, 1 \}$ であることを明示するときは、 $\Lambda_{\tau}$ と表現します。

格子 $\Lambda$ は、複素数の加法 $+$ を介して自然に加法が入ります。このことから $\Lambda$ はアーベル群の構造を持ち、 $\mathbb{C}$ の離散部分群となります。

ここで、 $\mathbb{C}$ を $\Lambda$ で割った $\mathbb{C}/\Lambda$ を（１次元）複素トーラスといいます。

図に表すと、こうなります。

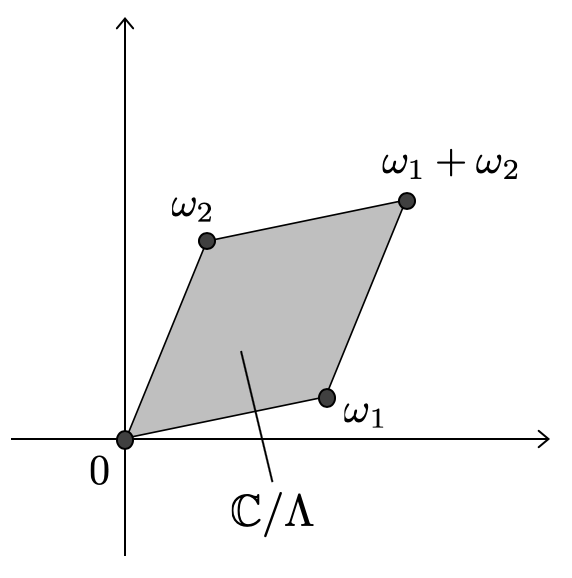
f:id:tsujimotter:20190707134918p:plain:w200

この平行四辺形の領域がなんで「トーラス」かというと、平行四辺形の左端と右端、上端と下端がそれぞれ同一視できるからです。図形としては、ドーナツ状の図形となります。

f:id:tsujimotter:20190707134950p:plain:w400

ところで、この複素トーラス $\mathbb{C}/\Lambda$ のことを（ $\mathbb{C}$ 上の）楕円曲線といいます。

「あれ？楕円曲線ってこういうやつ（ $E\colon y^2 = x^3 + ax + b$ ）じゃなかったっけ？」と思った方もいるかもしれません。

上記の方程式 $E$ の係数が $\mathbb{C}$ の元であるとき、これを（ $\mathbb{C}$ 上の）楕円曲線といいます。また、 $E$ の式を満たすような $(x, y) \in \mathbb{C}$ 全体と無限遠点の和集合を楕円曲線 $E$ の $\mathbb{C}$ 有理点といい、 $E(\mathbb{C})$ と表します。

実は、この $E(\mathbb{C})$ は、ある格子 $\Lambda$ が存在して $\mathbb{C}/\Lambda$ と解析的同型を持つことが知られています。

そんなの知らないよ、という方はこちらをどうぞ：
tsujimotter.hatenablog.com

そんなわけで、複素トーラスそのものを楕円曲線だと思うことができるわけですね。以下、この同一視のもと話を進めていきます。

2. 楕円曲線の射

$\mathbb{C}$ 上の楕円曲線を対象とする圏を考えたいと思います。このとき、射に相当するのが同種写像です。

同種写像は次のように定義します。

定義（同種写像）

$\mathbb{C}$ 上の楕円曲線 $\mathbb{C}/\Lambda$ から $\mathbb{C}/\Lambda'$ への 0 でない複素正則写像 $\phi$ で， $\phi(0) = 0$ であるものを $\mathbb{C}$ 上の同種写像という．

単なる複素正則写像だと、楕円曲線の単位元をもう一方の単位元に写してくれるとは限りません。そこで、 $\phi(0) = 0$ を課しています。

条件 $\phi(0) = 0$ と、 $\phi$ がアーベル群としての準同型であることは同値です。

命題1（同種写像の準同型性）

$\phi\colon \mathbb{C}/\Lambda \to \mathbb{C}/\Lambda'$ を $\mathbb{C}$ 上の同種写像とし， $z_1+\Lambda, \; z_2+\Lambda$ を $\mathbb{C}/\Lambda$ の点とする．このとき

$\phi(z_1+z_2+\Lambda) = \phi(z_1+\Lambda) + \phi(z_2+\Lambda)$

が成り立つ．

しかしながら、上記定義のままでは、同種写像のことがイメージできそうにありません。リウビルの定理などを用いると、上記の写像を具体的に表現することができます。

命題2

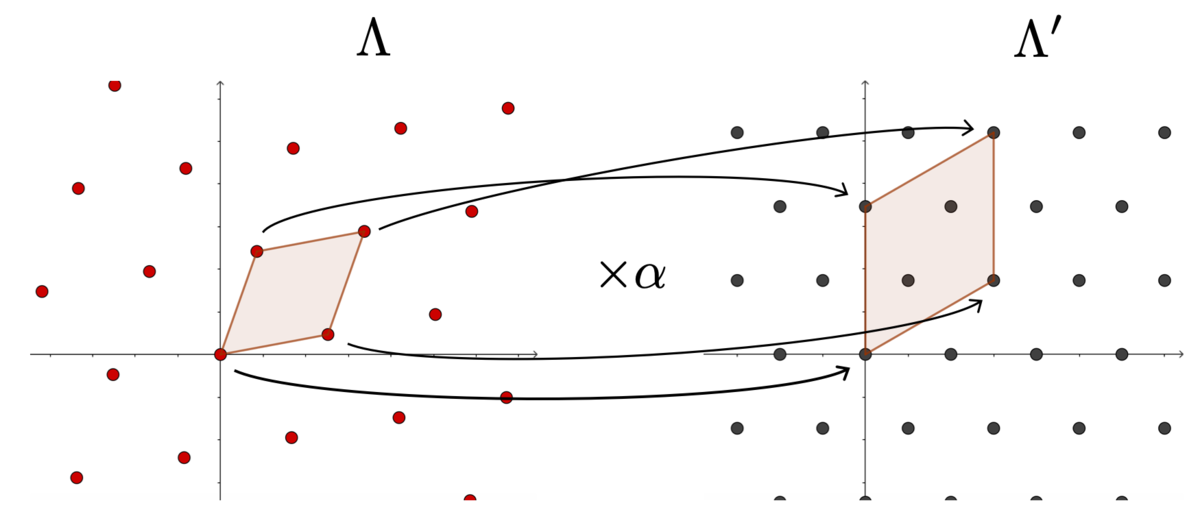
$\Lambda, \Lambda'$ を格子とするとき，以下の (i), (ii) は同値である．

(i) $\mathbb{C}$ 上の同種写像 $\phi\colon \mathbb{C}/\Lambda \to \mathbb{C}/\Lambda'$ が存在する．
(ii) $\alpha \Lambda \subset \Lambda'$ が成り立つような複素数 $\alpha \in \mathbb{C}^\times$ が存在する．

また，上記の (i), (ii) が成り立つとき， $\mathbb{C}/\Lambda$ の点 $z + \Lambda$ に対して

$\phi(z + \Lambda) = \alpha z + \Lambda'$

と表せる．

簡単にいってしまえば、同種写像が単なる「 $\alpha$ 倍写像」になってしまうということですね。

上の $\alpha$ 倍写像が well-defined であること、すなわち

$z_1 + \Lambda = z_2 + \Lambda \;\; \Longrightarrow \;\; \alpha z_1 + \Lambda' = \alpha z_2 + \Lambda'$

があることが気になりますが、それは次のように示されます。

（証明） $z_1 - z_2 \in \Lambda$ より

$\alpha(z_1 - z_2) \in \alpha \Lambda \subset \Lambda'$

が成り立つ．よって

$\alpha z_1 - \alpha z_2 \in \Lambda'$

より

$\alpha z_1 + \Lambda' = \alpha z_2 + \Lambda'$

である．

命題2はとても重要な命題で、特に楕円曲線の射が存在する必要十分条件が

$\mathbb{C}/\Lambda$ から $\mathbb{C}/\Lambda'$ への射が存在する
$\Longleftrightarrow \;\; \mathbb{C}/\Lambda$ から $\mathbb{C}/\Lambda'$ への $\mathbb{C}$ 上の同種写像が存在する
$\Longleftrightarrow \;\;$ $\alpha \Lambda \subset \Lambda'$ なる $\alpha \in \mathbb{C}^\times$ が存在する

と言い換えられることは極めて重要です。

最後の条件 $\alpha \Lambda \subset \Lambda'$ は図に表すとこんな感じです。

f:id:tsujimotter:20190707135018p:plain:w500

次に同型射について述べたいと思います。圏において、射 $f\colon A \to B$ が 同型射 であるとは、逆向きの射 $g\colon B \to A$ が存在して

$g\circ f = \operatorname{id}_{A}, \;\; f\circ g = \operatorname{id}_{B}$

が成り立つということです。

楕円曲線の圏においては、射は同種写像なので、同種写像 $\phi \colon \mathbb{C}/\Lambda \to \mathbb{C}/\Lambda'$ が同型射であるとは、逆向きの同種写像 $\phi' \colon \mathbb{C}/\Lambda' \to \mathbb{C}/\Lambda$ が存在して

$\phi' \circ \phi = \operatorname{id}_{\mathbb{C}/\Lambda}, \;\; \phi \circ \phi' = \operatorname{id}_{\mathbb{C}/\Lambda'}$

が成り立つことをいいます。

２つの楕円曲線 $\mathbb{C}/\Lambda, \mathbb{C}/\Lambda'$ の間に同型射が存在するとき、 $\mathbb{C}/\Lambda$ と $\mathbb{C}/\Lambda'$ は同型であるといい

$\mathbb{C}/\Lambda \simeq \mathbb{C}/\Lambda'$

と表します。

ところで、命題2によると楕円曲線の任意の射は「 $\alpha$ 倍写像」なのでした。よって、次が言えます。

命題3

$\Lambda, \Lambda'$ を格子とする．このとき，以下の (i), (ii) は同値である：

(i) 同型射 $\phi \colon \mathbb{C}/\Lambda \to \mathbb{C}/\Lambda'$ が存在する
(ii) $\alpha \Lambda = \Lambda'$ が成り立つような複素数 $\alpha \in \mathbb{C}^\times$ が存在する

同種写像の必要十分条件は $\alpha \Lambda \subset \Lambda'$ でしたが、同型射の場合は $\alpha \Lambda = \Lambda'$ であるということですね。

また、楕円曲線の同型は同値関係の条件を満たします。そこで、楕円曲線の同型類全体の集合を

$\mathcal{ELL}_{\mathbb{C}} := \{ \mathbb{C}\,\text{上の楕円曲線}\,\mathbb{C}/\Lambda \, \text{全体}\}/\simeq$

と表すことにします。この $\mathcal{ELL}_{\mathbb{C}}$ の元で、楕円曲線 $\mathbb{C}/\Lambda$ の同型類を

$[ \mathbb{C}/\Lambda ] := \{ \mathbb{C}/\Lambda' \mid \mathbb{C}/\Lambda \simeq \mathbb{C}/\Lambda' \}$

とします。

3. 上半平面 H と楕円曲線

上半平面 $H$ とは、複素数平面の上半分のことです。

$H := \{ \tau \in \mathbb{C} \mid \operatorname{Im}(\tau) > 0 \}$

楕円曲線は、上半平面上の点 $\tau \in H$ で表現できるということを示したいと思います。

基底 $\{ \omega_1, \omega_2 \}$ を明示した任意の格子 $\Lambda_{\omega_1, \omega_2}$ について、対応する楕円曲線 $\mathbb{C}/\Lambda_{\omega_1, \omega_2}$ を考えます。また、 $\omega_1, \omega_2$ の順番はどちらでも格子は変わらないので、 $\operatorname{Im}(\omega_1/\omega_2) > 0$ となるように正規化しても一般性は失いません。

このとき、 $\Lambda_{\omega_1, \omega_2}$ を $\omega_2$ で割った格子

$\displaystyle \frac{1}{\omega_2}\Lambda_{\omega_1, \omega_2}$

を考えると、これは $\tau = \omega_1/\omega_2$ として、基底を $\{ \tau, 1 \}$ とする格子と一致します。すなわち

$\displaystyle \frac{1}{\omega_2}\Lambda_{\omega_1, \omega_2} = \Lambda_{\tau}$

ということです。

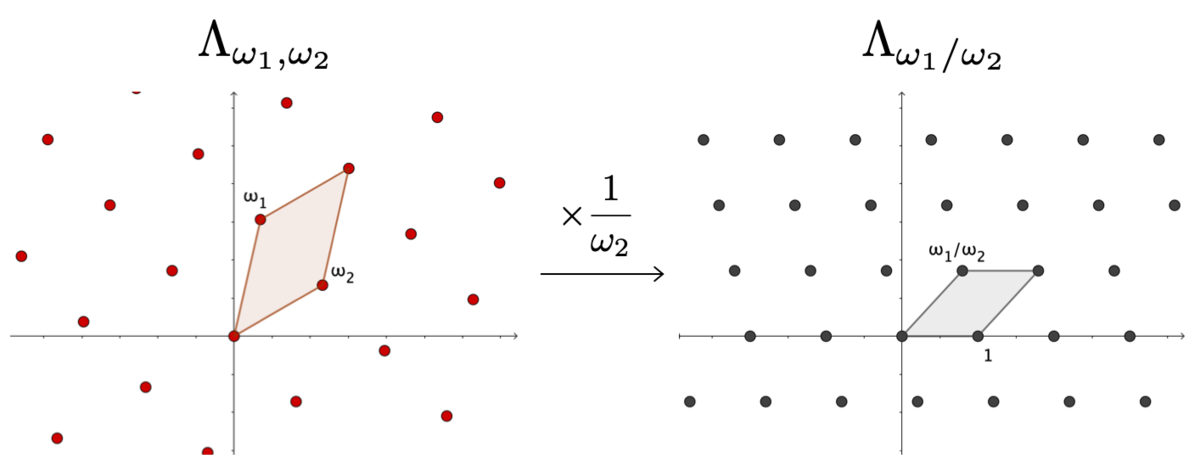
f:id:tsujimotter:20190707140419p:plain:w500

このことは、 $\mathbb{C}/\Lambda_{\omega_1, \omega_2}$ と $\mathbb{C}/\Lambda_\tau$ が同型であることを示しています。このとき $\tau \in H$ なので、次が言えます。

命題4

任意の $\mathbb{C}$ 上の楕円曲線 $E = \mathbb{C}/\Lambda$ に対して、 $\tau \in H$ が存在して

$E \simeq \mathbb{C}/\Lambda_{\tau}$

が成り立つ．

すなわち、上半平面 $H$ 上には、 $E$ に対応する点が存在するということですね。

4. 楕円曲線のモジュライ空間

上で示した楕円曲線と上半平面の対応は、一対一対応ではありません。上半平面上の一点には、同型な楕円曲線が無数に対応しますし、逆に楕円曲線に対応する点も無数に存在します。

この対応関係をきれいな全単射にするために、「楕円曲線の同型写像」と「上半平面の変換」の間の関係性を探ります。

実は、楕円曲線の同型射 $\phi \colon \mathbb{C}/\Lambda_{\tau} \to \mathbb{C}/\Lambda_{\tau'}$ は、 $\tau, \tau' \in H$ の間のモジュラー変換と呼ばれる変換に対応しています。

整係数かつ行列式が 1 であるような2次正方行列全体のなす群をモジュラー群といい、 $\operatorname{SL}_2(\mathbb{Z})$ で表します。すなわち

$\operatorname{SL}_2(\mathbb{Z}) := \left\{ \gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \; \middle| \;\; a, b, c, d \in \mathbb{Z}, \; ad - bc = 1 \right\}$

ということです。　

モジュラー群 $\operatorname{SL}_2(\mathbb{Z})$ の元 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ は、次のように $\tau \in H$ に作用します：

$\displaystyle \gamma\tau := \frac{a\tau + b}{c\tau + d}$

これをモジュラー変換といいます。要するに、モジュラー群 $\operatorname{SL}_2(\mathbb{Z})$ に関する一次分数変換のことをモジュラー変換というわけですね。

ここで、以下の命題が成り立ちます。

命題5

$\tau, \; \tau' \in H$ としたとき，以下の (i), (ii) は同値である．

(i) $\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$
(ii) $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ が存在して $\tau = \gamma \tau'$

つまり、楕円曲線の同型射と $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ がちょうど一対一対応しているということですね。

上の命題5を直接証明してもいいのですが、以下の補題6を使うと随分証明が楽になります。

補題6

$\omega_1, \omega_2, \omega_1', \omega_2' \in \mathbb{C}$ を $\operatorname{Im}(\omega_1/\omega_2) > 0, \; \operatorname{Im}(\omega_1'/\omega_2') > 0$ となるようにとるとき，以下の (i), (ii) は同値である．

(i) $\Lambda_{\omega_1, \omega_2} = \Lambda_{\omega_1', \omega_2'}$
(ii) $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ が存在して，次が成り立つ：

$\displaystyle \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \gamma \begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix}$

この補題は、２組の基底 $\{\omega_1, \omega_2\}, \; \{\omega_1', \omega_2'\}$ で表された格子が同じものであるような必要十分条件を与えます。

補題6の証明は少し難しいので後に回します。ここでは、補題6を使うと命題5が証明できることを示しましょう、

（命題5の証明）

(i) $\Longrightarrow$ (ii) を示す：
楕円曲線の同型 $\mathbb{C}/\Lambda_\tau \simeq \mathbb{C}/\Lambda_{\tau'}$ があると仮定します。楕円曲線の同型射の必要十分条件（命題3）より、 $\alpha \in \mathbb{C}^\times$ があって $\alpha \Lambda_{\tau} = \Lambda_{\tau'}$ が言えます。

$\alpha \Lambda_{\tau} = \Lambda_{\alpha \tau, \alpha}$ より

$\Lambda_{\alpha \tau, \alpha} = \Lambda_{\tau', 1}$

が成り立ちます。

ここで補題6の (i) $\Longrightarrow$ (ii) より、 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}_2(\mathbb{Z})$ が存在して

$\displaystyle \begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

と表せます。よって

$\displaystyle \tau = \frac{\alpha \tau}{\alpha} = \frac{a\tau' + b}{c\tau' + d} = \gamma \tau'$

より、 $\tau = \gamma \tau'$ が言えました。

(ii) $\Longrightarrow$ (i) を示す：
$\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}_2(\mathbb{Z})$ が存在して

$\displaystyle \tau = \frac{a\tau' + b}{c\tau' + d}$

と仮定します。

ここで、 $\alpha = c\tau' + d$ とおきます（ここが重要！）。

このとき

$\displaystyle \alpha \tau = (c\tau' + d)\frac{a\tau' + b}{c\tau' + d} = a\tau' + b$

となり

$\displaystyle \begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

と表せます。

ここで補題6の (i) $\Longrightarrow$ (ii) より

$\Lambda_{\alpha \tau, \alpha} = \Lambda_{\tau', 1}$

が成り立ちます。

よって、 $\alpha \Lambda_{\tau, 1} = \Lambda_{\tau', 1}$ より $\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$ が言えました。

補題6のおかげでこれでもだいぶ短くなっています。この「ちょうどぴったり格子が一致することの必要十分条件」を与えているというのが補題6の便利な点です。また次回の記事でこれを使います。

証明の途中で「ここが重要！」と書いたところですが、格子の間の同型射が

$\alpha = c\tau' + d$

として「 $\alpha$ 倍写像」と具体的に表せるということですね。これはまた次回使うことでしょう。

さて、命題5が証明できたことで、楕円曲線の同型類と上半平面の対応関係が明らかになります。

$\operatorname{SL}_2(\mathbb{Z})\backslash H$ を、 $H$ をモジュラー群 $\operatorname{SL}_2(\mathbb{Z})$ の作用によって割ってできた同値類全体としましょう。すなわち $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ が存在して

$\tau = \gamma \tau'$

を満たすとき、 $\tau \sim \tau'$ という同値関係を入れます。この同値関係で割ったものが $\operatorname{SL}_2(\mathbb{Z})\backslash H$ です。これをモジュラー群 $\operatorname{SL}_2(\mathbb{Z})$ に対するモジュラー曲線といい、 $Y(1)$ で表します。

また、モジュラー曲線 $Y(1)$ の元は、任意の $\tau \in H$ を代表元とする同値類

$[ \tau ] := \{ \tau' \in H \mid \tau \sim \tau' \}$

となります。

このモジュラー曲線の詳細は、以下で読んでいただくとします。

参考：
tsujimotter.hatenablog.com

ここで議論したいのは、以下の命題7です。

命題7

$\mathcal{ELL}_{\mathbb{C}}$ を $\mathbb{C}$ 上の楕円曲線の同型類全体の集合としたとき，次の写像は全単射である：

$\begin{matrix} Y(1) & \longleftrightarrow & \mathcal{ELL}_{\mathbb{C}} \\ [\tau ]& \longmapsto & [\mathbb{C}/\Lambda_{\tau}] \end{matrix}$

命題7が言っていることは、モジュラー曲線 $Y(1)$ の任意の点には、対応する楕円曲線の同型類があり、それが全単射になっているということです。

f:id:tsujimotter:20190707141823p:plain:w400

このような状況を、モジュラー曲線 $Y(1)$ は楕円曲線の同型類のモジュライ空間であるといいます。モジュライ空間とは「図形や曲線のパラメータ全体の空間」のような意味ですが、 $Y(1)$ は　まさにそのような空間になっていますね。

最後に、命題4と命題5を使って、命題7を証明して終わりにしましょう。

（命題7の証明）
$Y(1) \longrightarrow \mathcal{ELL}_{\mathbb{C}}$ の well-defined 性を示す：
$\tau \sim \tau' \; \Longrightarrow \; \mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$ が
言えればよいが、これは命題5の (ii) $\Longrightarrow$ (i) より言える。

$Y(1) \longrightarrow \mathcal{ELL}_{\mathbb{C}}$ の単射性を示す：
$\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'} \; \Longrightarrow \; \tau \sim \tau'$ が
言えればよいが、これは命題5の (i) $\Longrightarrow$ (ii) より言える。

$Y(1) \longrightarrow \mathcal{ELL}_{\mathbb{C}}$ の全射性を示す：
任意の楕円曲線の同型類 $[\mathbb{C}/\Lambda ] \in \mathcal{ELL}_{\mathbb{C}}$ に対して、 $[\mathbb{C}/\Lambda ] = [\mathbb{C}/\Lambda_{\tau} ]$ なる $\tau \in H$ が存在することが言えればよいが、これは命題4より言える。

証明おしまいです。お疲れ様でした。

5. おわりに

今回は、複素トーラスとしての楕円曲線の基本的な性質

楕円曲線の射、同型射
楕円曲線の同型類のモジュライ空間

について説明しました。

モジュラー曲線シリーズの次回は、モジュラー曲線 $Y_1(N)$ や $Y_0(N)$ について、モジュライ空間としての構造を説明したいと思います。補題6は次回も使う予定ですので、確認しておいてください。

それでは今日はこの辺で。

補足：補題6の証明

補足として、補題6の証明を行います。証明の前に、補題を再掲しておきます。

補題6（再掲）

(i) $\Lambda_{\omega_1, \omega_2} = \Lambda_{\omega_1', \omega_2'}$
(ii) $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ が存在して，次が成り立つ：

$\displaystyle \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \gamma \begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix}$

（補題6の証明）

(i) $\Longrightarrow$ (ii) を示す：
$\Lambda_{\omega_1, \omega_2} = \Lambda_{\omega_1', \omega_2'}$ を仮定します。

$\omega_1, \omega_2$ は、 $\Lambda_{\omega_1', \omega_2'}$ の基底によって表せるので、 $a, b, c, d \in \mathbb{Z}$ が存在して

$\begin{cases} \omega_1 = a\omega_1' + b\omega_2' \\ \omega_2 = c\omega_1' + d\omega_2' \end{cases}$

が成り立ちます。すなわち

$\begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix} \tag{a}$

です。

同様に $\omega_1', \omega_2'$ は、 $\Lambda_{\omega_1, \omega_2}$ の基底によって表せるので、 $e, f, g, h \in \mathbb{Z}$ が存在して

$\begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix} = \begin{pmatrix} e & f \\ g & h \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} \tag{b}$

と表せます。

式 $(b)$ を式 $(a)$ に代入すると

$\begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} e & f \\ g & h \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix}$

が成り立ちます。

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} e & f \\ g & h \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix}$

とおくと

$\begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix}$

ですが

$\begin{cases} (A - 1)\omega_1 + B\omega_2 = 0 \\ C\omega_1 + (D - 1) \omega_2 = 0 \end{cases}$

であることと、 $\{\omega_1, \omega_2\}$ が $\mathbb{R}$ 上1次独立であること（格子の2番目の条件）から

$A = 1, B = 0, C = 0, D = 1$

がわかります。

すなわち

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} e & f \\ g & h \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

が言えました。

つまり、整係数行列 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ が同じく整係数行列である逆行列を持つということですが、このことから

$ad - bc = \pm 1 \tag{c}$

が言えます。

また

$\displaystyle \frac{\omega_1}{\omega_2} = \frac{a\omega_1' + b\omega_2'}{c\omega_1' + d\omega_2'} = \frac{a\frac{\omega_1'}{\omega_2'} + b}{c\frac{\omega_1'}{\omega_2'} + d} \tag{d}$

です。

ここで、右辺において $\tau = \omega_1' / \omega_2' = s + it$ とし、分母を有理化すると

$\displaystyle \frac{a\tau + b}{c\tau + d} = \frac{ \{ ac|\tau|^2 + (ad + bc)s + bd\} + \{ (ad - bc)t \}i }{|c\tau + d|^2}$

となるため、式 $(d)$ の両辺の虚部をとると

$\displaystyle \operatorname{Im}\left(\frac{\omega_1}{\omega_2}\right) = \frac{(ad - bc) \operatorname{Im}\left(\frac{\omega_1'}{\omega_2'}\right) }{\left|c \frac{\omega_1'}{\omega_2'} + d\right|^2}$

が得られます。

仮定より $\operatorname{Im}(\omega_1/\omega_2) > 0$ かつ $\operatorname{Im}(\omega_1'/\omega_2') > 0$ であるから

$ad - bc > 0 \tag{e}$

が得られました。式 $(c)$ と式 $(e)$ より

$ad - bc = 1$

が得られたので、 $\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}_2(\mathbb{Z})$ が言えました。

(ii) $\Longrightarrow$ (i) を示す：
$\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}_2(\mathbb{Z})$ が存在して

$\begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix} \tag{a}$

が成り立つと仮定します。

よって

$\begin{cases} \omega_1 = a\omega_1' + b\omega_2' \\ \omega_2 = c\omega_1' + d\omega_2' \end{cases}$

です。ここで、 $\Lambda_{\omega_1, \omega_2}$ の任意の元は $n \omega_1 + m \omega_2$ と表せるが

$\begin{align} n \omega_1 + m \omega_2 &= n (a\omega_1' + b\omega_2') + m (c\omega_1' + d\omega_2') \\ &= (na + mc)\omega_1' + (nb + md)\omega_2' \in \Lambda_{\omega_1', \omega_2'} \end{align}$

となります。よって $\Lambda_{\omega_1, \omega_2} \subset \Lambda_{\omega_1', \omega_2'}$ が言えます。

一方、

$\begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}^{-1} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \begin{pmatrix} e & f \\ g & h \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix}$

に対して同様にすると、任意の $\Lambda_{\omega_1', \omega_2'}$ の元 $n'\omega_1' + m'\omega_2'$ に対して $n'\omega_1' + m'\omega_2' \in \Lambda_{\omega_1, \omega_2}$ が言えます。よって $\Lambda_{\omega_1', \omega_2'} \subset \Lambda_{\omega_1, \omega_2}$ が言えます。

以上により、 $\Lambda_{\omega_1, \omega_2} \subset \Lambda_{\omega_1', \omega_2'}$ と $\Lambda_{\omega_1, \omega_2} \supset \Lambda_{\omega_1', \omega_2'}$ が言えたので、 $\Lambda_{\omega_1, \omega_2} = \Lambda_{\omega_1', \omega_2'}$ が言えました。