前回、指数関数の3つの素朴な性質から
なる2つの短完全列が得られることを紹介しました。
本シリーズタイトルの指数層系列とは、上の短完全列を層の間の短完全列に伸ばしたものです。今日は、層の理論をまとめつつ、指数層系列を得るところまでいきたいと思います。
最初のうちは、上記の話を単に層の言葉で表せばよいだけと思っていました。ところが、勉強していくうちに、そこまで単純な話ではないということに徐々に気づいてきました。私自身、正しい理解に大変苦労しまして、記事の内容も二転三転しています。その辺の戸惑いやそれを乗り越えて理解したときの感覚などは、なかなか本には載っていない部分と思います。その辺をできるだけ残そうという趣旨で書いています。参考になれば幸いです。
勉強する際は、私の記述をうのみにせず参考文献をご参照いただければと思います。参考文献は一番下に書いています。
それでは少し長いですが、お付き合いください。
目次:
3. すべてが層になる
式 の短完全列の登場人物
は、すべて正則関数のなすアーベル群でした。これらをすべて
上の層に置き換えることを考えましょう。
任意の開集合 に対して、対応関係
を考えると、「 上の開集合全体が包含関係に対してなす圏」から「アーベル群のなす圏」への反変関手になっています。すなわち前層です。さらにいえば、次の記事で議論したように層の条件も満たすことがいえます。
tsujimotter.hatenablog.com
層の完全列として議論するためには、 も層として考える必要があります。しかしながら、単純に開集合
に対して定数関数のなす群
を割り当てるだけでは、前層にはなるものの層の条件を満たしません。
具体的にどういうことか説明しましょう。
上の開集合
に対して、
の開被覆
を考えます。特に、
の交わりはない(
)ものとします。この条件で層
の
における切断
を考えましょう。
もし仮に、 であるとします。
はそれぞれ定数関数です。
は共通部分を持たないので、上の記事の例2で議論したように、層の閉条件から
の元
で
を満たすようなものが存在しなければなりません。
がともに同じ値を関数値に持つ定数関数であれば、
も定数関数です。しかしながら、
がどちらも異なる定数値である場合は
は明らかに定数関数ではありません。たとえば、
上で
、
上で
になるような関数も、
に入っている必要があります。
このように、連結成分ごとに定数関数になるような関数のことを局所定数関数といいます。切断 として、
上定義される(特定のクラスの)局所定数関数全体を対応付けることで得られる層
のことを定数層といいます。「局所定数」関数なのに、「定数」層と呼ぶのがややこしいですが、そのように覚えましょう。*1
以上を踏まえて、各連結成分に対して の値をとる定数関数を対応させる定数層を、改めて
と表すことにします。
また、層 の開集合
における切断をそれぞれ
と表すことにします。
実際、前回補足的に議論したように、 個の連結成分をもつ開集合
上で
を考えると、その核は
に一致するのでした。
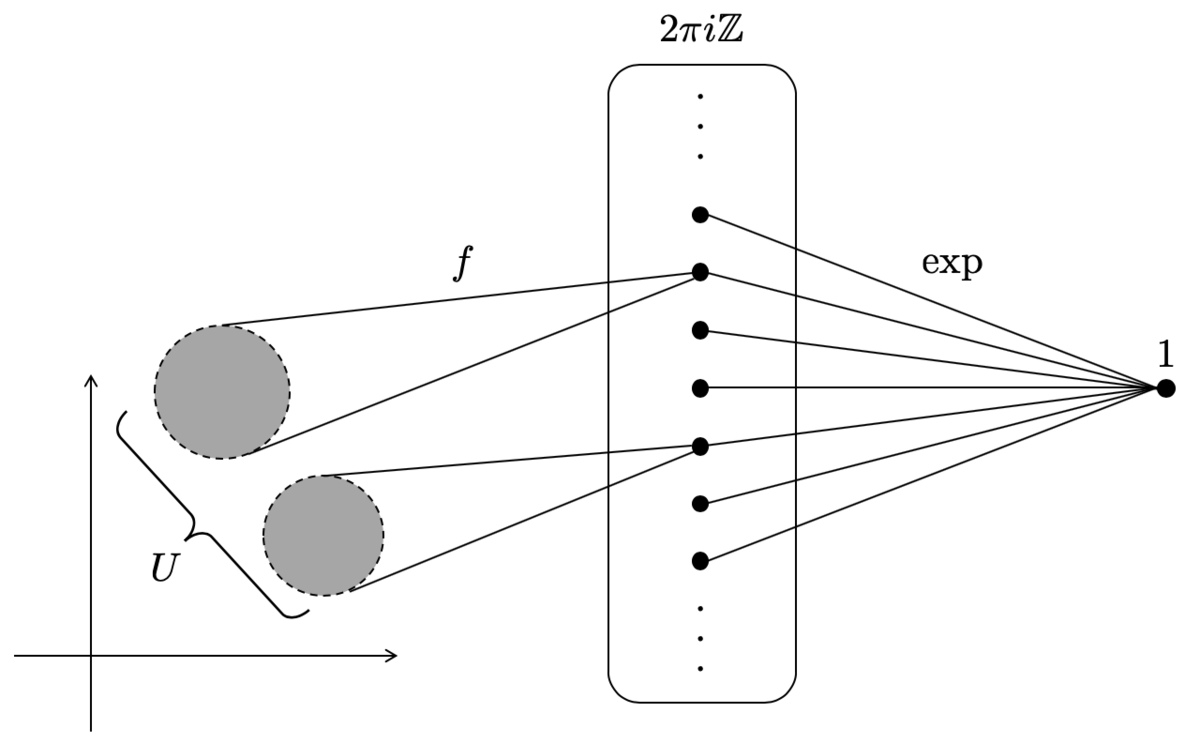
(前回の図を再掲)
ですから、まさに定数層
の
における切断を表していたというわけです。
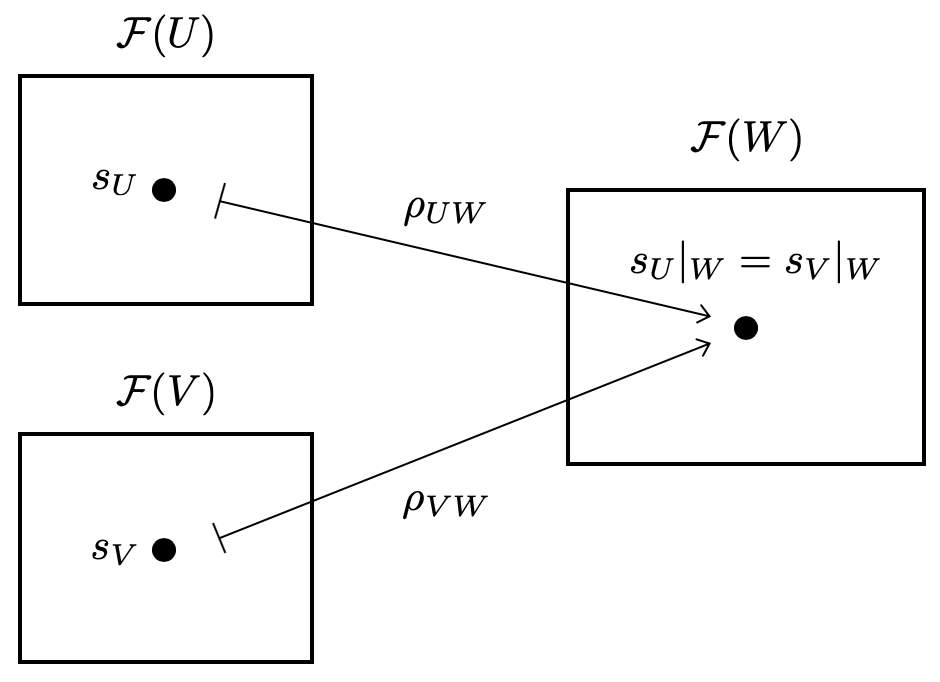
4. 順極限と茎
ここでは層における重要概念である「茎(ストーク)」について、少し丁寧にまとめておきたいと思います。層の完全列を考える上でも重要ですし、上で定義した定数層を茎を使って再定義することもできます。
上の点
を含むような開集合全体
を考えます。
の開集合
の間に
という包含関係があったとき、前層
の切断
を考えると、制限写像
が入ります。開集合が大きい方から小さい方に向かって射が入っていることに注意します。
制限写像の射の向きに合わせて、 という順序を入れた集合
に対して、対象
と射
の組は順系をなします。
順系 に対して順極限が次のように定義できます。
この を、前層
の
における茎(ストーク)といって
で表すことにします。茎は層だけでなく、一般の前層に対して定義できることに注意します。
という集合に対する直和とは
という集合のことです。すなわち、各集合の元に「どこの集合からきたのか」というラベルをつけて並べたものです。なので、 にはどちらも
という元がありますが、直和の元としては
のように区別しようということです。
また、順極限の定義 においては「同値関係
で割る」という操作が入っていますが、これは次のように定義されます。
に対して
であるとは、順系
においてある
が存在して
なる射があり
であること、として定義します。
すなわち、順系で進んでいった先にある同じ で
と
が等しければ、
であるということですね。
具体例として、 を含む開集合全体を
として、
なる包含関を考えます。この包含関係によって誘導される制限写像
のなす順系を考えましょう。特に、各切断の元の行き先が、具体的に次の図のようになっている状況を考えます。
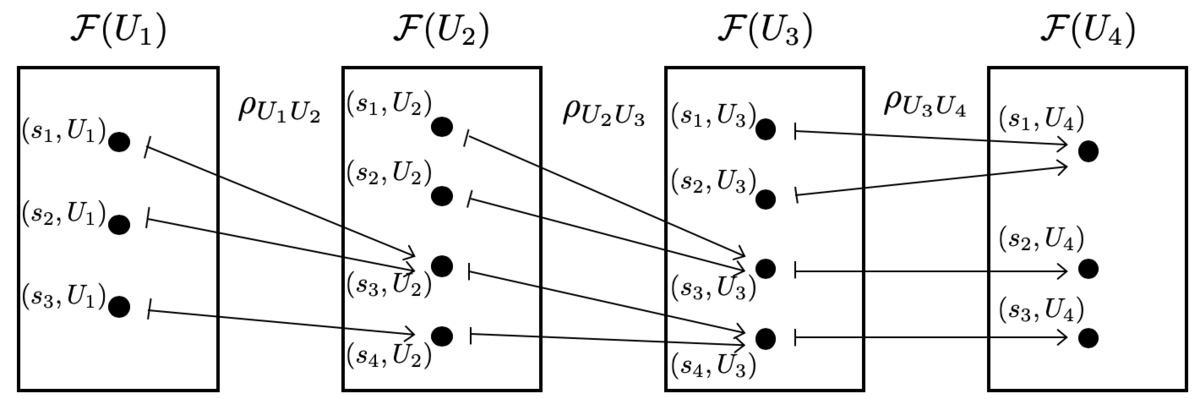
このとき、前層 の
における茎は
となりますね。
なので、 の元だけで順極限の同値類がすべて表せます。よって、簡単に
とかけてしまいますね。
以下のように、制限写像で繋がっている「枝分かれした線」を の元だと思ってもいいでしょう。
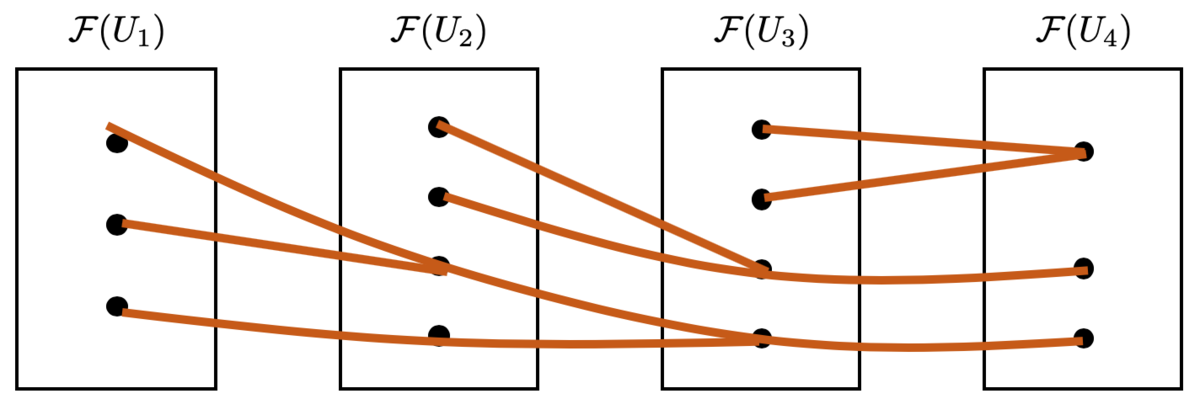
まさに茎という感じがしてきませんか?(僕だけですか?)
上では順系の対象が有限個の場合を考えましたが、無限個の場合も同様に考えることができます。この場合も制限写像で行った先でまとまった元たちについては同じものとみなしているので、「枝一本」が茎の元となります。
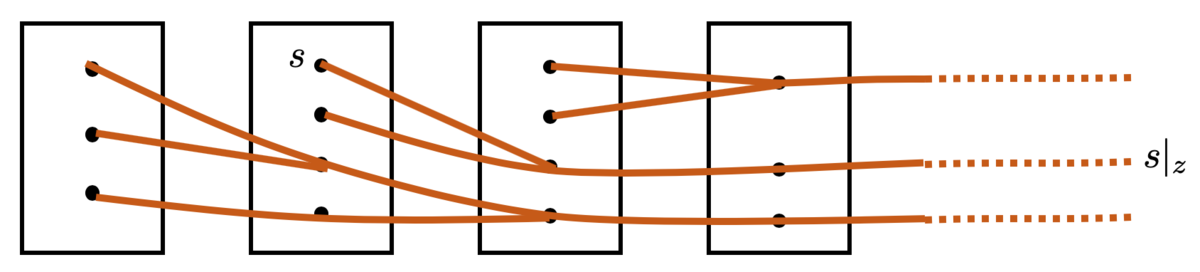
あとで使うので、 の
のまわりでの極限を
と表すことにします。すなわち、次の写像の行き先が
です:
茎という概念が、層の完全性を考えるにあたって重要な役割を果たすのですが、これについてはまた後の節で議論したいと思います。
ここでは「層化」という操作について説明したいと思います。前層 が与えられたときに(これは一般に層ではありませんが)、
から層を作り出す操作があります。
前層 には、任意の点
における茎
を考えることができます。すべての
について、閉条件による整合性がとれるよう、各開集合における切断を構成していって得られた層
を、前層
の層化(sheafification)といいます。
具体的には、任意の開集合 に対して、
を次のように対応させればよいでしょう。
定義からわかるように、 は直積
の部分集合です。
イメージ的には、各点における茎は残しつつ、その上の開集合における切断については層の条件を満たすよう作り変えてしまったもの、ということでしょうか。つまり、層化する前と後では、茎だけは一緒ですが、それ以外はまったく別物と考えてしまった方がいいかもしれません。
前節の例で考えると、任意の開集合 に対して
と対応させると
は前層です。
の層化が定数層
というわけですね。
5. 層の準同型と完全性
上の正則関数のなす3種類の層
を定義しました。任意の開集合
における切断をそれぞれ考えると
となります。前回の記事における議論により、これらの間にはアーベル群の準同型が存在し、次の短完全列
が成立します。
一つの開集合 に対して一つの短完全列が得られるので、開集合の数だけずらっと短完全列が得られるというわけです。
これから、上の完全列を延長して「層として」の短完全列を作りたいと思います。
層としての完全列を考えるにあたっては、「層の準同型(射)」と「完全性」について定義する必要があります。
まずは層の準同型から定義したいと思います。前層 に対して、
が前層の準同型(あるいは、前層の射)であるとは、任意の開集合の包含関係
に対して
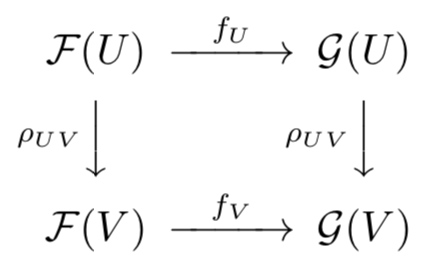
が可換であることをいいます。 がどちらも層であるとき、
は層の準同型(あるいは、層の射)であるといいます。
たとえば、任意の開集合の包含関係 に対して
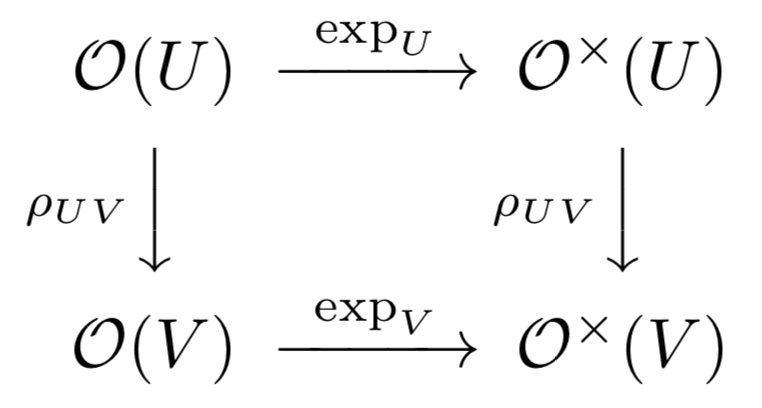
が可換であることを示しましょう。次の図式
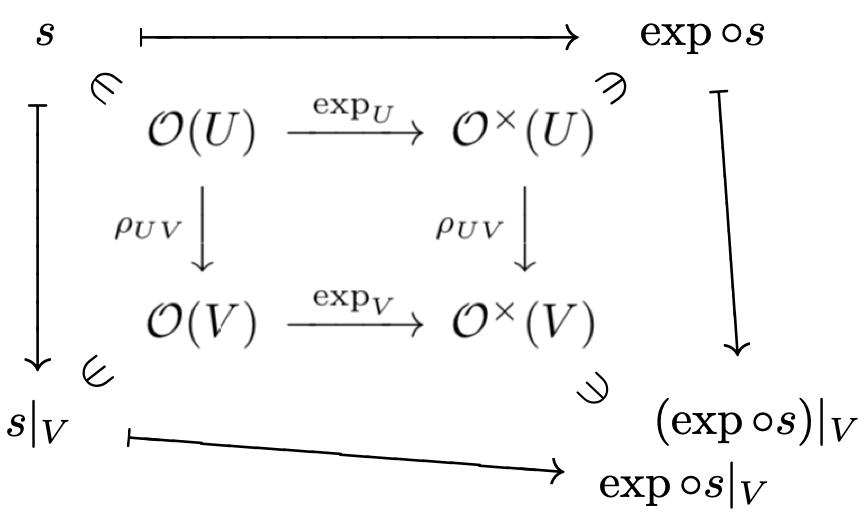
に対して制限写像との可換性
を示せばよいですが、これは明らかに成り立ちますね。よって、指数写像 は層
の間の(層としての)準同型です。
完全性の定義には、層の準同型に対して を定義する必要があります。これも、個々の開集合
に対するアーベル群の準同型の
によって定義されます。
Kerと単射性
を前層の準同型とします。任意の開集合
に対して、アーベル群の準同型写像
の核 を対応づけるルール
を とします。このとき、定義から明らかに
はアーベル群としての完全列となります。
は
の制限写像
から誘導される制限写像を考えることで前層になります。また、一般に
が層の準同型のとき(つまり、
のどちらも層であるとき)、
も層になります。
ここで、 の単射性を以下のように定義します:
- 前層の準同型
において
であるとき、
は単射であるといいます。
- 層の準同型
において
であるとき、
は単射であるといいます。
ややこしく書いてしまいましたが、単射性については が「前層の準同型」か「層の準同型」かは特に気にする必要はありません。層の準同型
は
のとき、すなわち、すべての切断において
が単射であるそのときに限り、前層としても層としても単射となります。
実は、次の全射性においては、前層としての準同型なのか、層としての準同型なのかを真に考える必要があります。
Cokerと全射性(要注意)
を前層の準同型とします。任意の開集合
に対して
の余核
を対応づけるルール
を とします。このとき、任意の開集合
に対し
はアーベル群としての完全列となることに注意しましょう。
は、
から誘導される制限写像により
上の前層となりますが、一般に層にはなりません。そこで、
の層化を
とします。
ここで、 の全射性を以下のように定義します:
- 前層の準同型
において
であるとき、
は全射であるといいます。
- 層の準同型
において
であるとき、
は全射であるといいます。
単射の場合と異なり「前層の準同型」か「層の準同型」かで違いが出てきました。
これは大いに注意しておきたいことなのですが、層の準同型 が全射であったとしても、前層としては全射であるとは限りません。実は、このあと紹介する指数層系列がまさにそのような例になっています。
逆に、前層として全射であれば、 よりその層化も
になります。したがって、層としても全射となります。
また、前層として全射であれば、任意の開集合 に対し
より
はアーベル群としての完全列となることに注意しましょう。
一方で、層として全射であったとしても、任意の開集合 に対して
にならないことに注意しましょう。
完全性
ここでようやく「完全性」について定義ができます。前層 と前層の準同型
に対して
が複体であるとは、すべての について
であることをいいます。
複体であるとき、 の「普遍性」とよばれる性質から、以下の図式を可換にするような前層の準同型
が一意的に得られます。
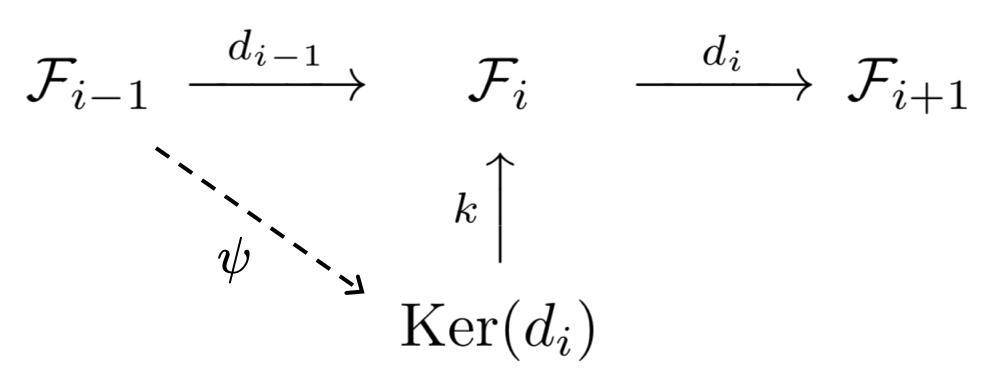
- 式
が前層の準同型の列であり前層の準同型
が全射であるとき(すなわち
)、前層の準同型の列
は
において完全であるといいます。
- 式
が層の準同型の列であり層の準同型
が全射であるとき(すなわち
)、層の準同型の列
は
において完全であるといいます。
ハーツホーンの「代数幾何学」では で定義しているのですが、今回は寺杣先生の「リーマン面の理論」の記述に従いました。
よくよくみると、ほとんど同じことを言っているかと思いますが、正確には理解できていません。
6. 指数層系列
以上を踏まえて、長かったですがようやく「指数層系列」の主張を述べることができます。
前回の記事で紹介した指数関数の短完全列を、ついに層の短完全列まで持ち上げることができたというわけですね。これを指数層系列(exponent sheaf sequence)といいます。
全射の項で述べたように、任意の開集合 に対し、
上の切断において完全であることは、指数層系列からは直ちに導くことはできません。実際、開集合
が単連結でない場合に、
が全射でないことを前回示したのでした。
以下では、指数層系列を証明したいと思います。まず
が前層の準同型として完全であることは、次の①②から言うことができます。
- ①任意の開集合
に対する切断がアーベル群として完全である
(これは前回の記事で示したことですね)
- ②準同型が制限写像と可換である。つまり、層の準同型の完全列である。(これも上で示しましたね。)
よって、前層の完全列であることが示せたので、以下の命題の (ii) より層の完全列であることも言えます。
(ii) を層の準同型の列とする。このとき次が成り立つ:
問題は、層の準同型として
が完全であることです。これはすなわち、層の準同型 の全射性を示したいということです。
7. 指数層系列の全射性
ここで使えるのが茎です。ここでは示しませんが、次の命題が成り立ちます。
は全射である
任意の
に対して
におけるアーベル群の準同型
が全射である
(「全射」を「単射」に置き換えても成り立つ。)
したがって、任意の点における茎の全射性を確認すれば良いことになります。すなわち示すべきは、任意の に対して
の全射性です。
茎の間の全射は、実際どうやって示したらよいのでしょうか。素朴にいうなら、示すべきことは、こういうことでしょうか。
任意の の近傍
に対して、任意の
を考える。これに対して、ある
の近傍
で
となるような が存在することを示せばよい。
言葉だとわかりづらいかもしれませんが、図で表すとわかるかもしれません。
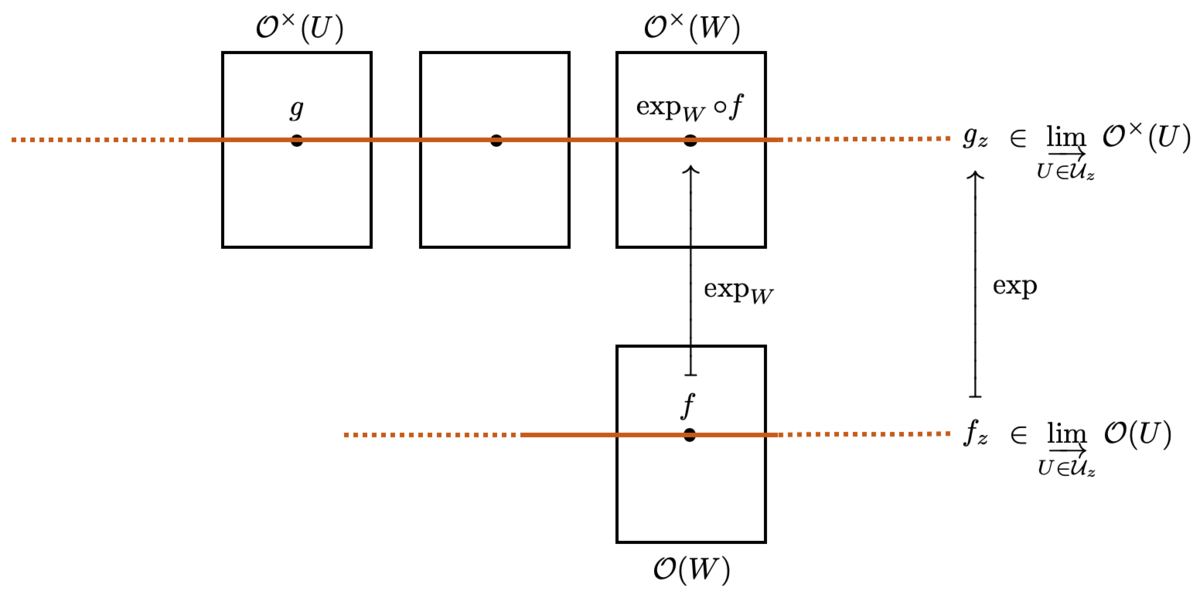
実際やってみましょう。
(証明) を含む任意の開集合全体を
とします。任意の
に対して、任意の
を考えます。このとき
の定義より
です。
これに対して、ある であり
であるような十分小さい開集合
をとります。たとえ
が 0 の周りをまわるループを領域内に持っていたとしても、
を十分小さくとることで
の任意のループが 0 の周りをまわらないようにできます。
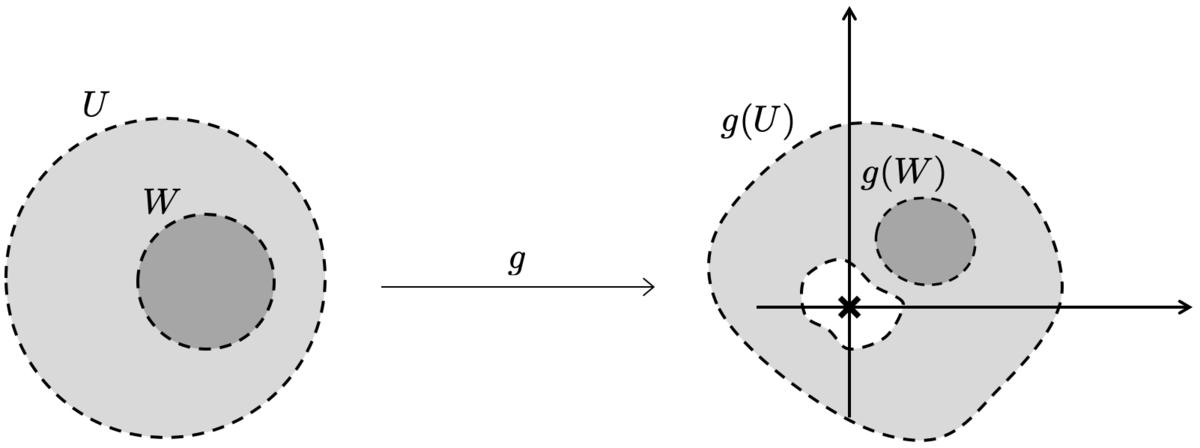
ある を含む
の開集合
で、
であり「
内の任意のループが 0 の周りをまわらないようなもの」をとります。
における
の逆像
を考えると、正則関数 は連続写像より、
は開集合です。したがって、
ととれば、所望の開集合が得られます。
ここで に対して
で定義される関数を考えます。
十分近い に対して、
の値が決まると
を十分近い値に決めることができます。
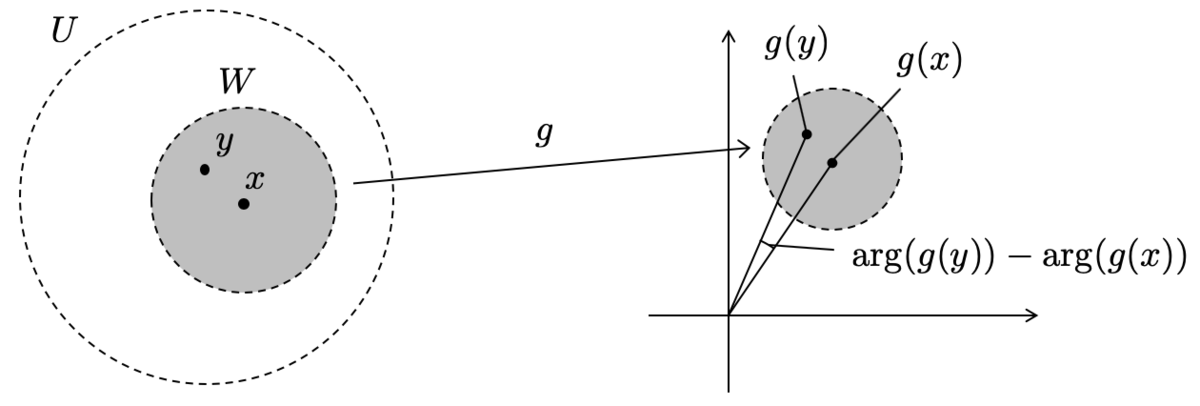
これを連続的に行うことで、任意の に対し
の値を連続的に決定することができ、
は
上の1価正則な関数になります。
よって とすると
となります。
茎の定義を思い出すと、 における茎
の元は、同値関係「
の十分小さい近傍で一致していれば同じものである」で割った同値類でした。上の
と
は
上で一致するので
です。すなわち、 と
は
において同じ元を定めます。
以上により、任意の の元
に対し
なる の元
をとることができましたので、
は全射であることが示されました。(証明おわり)
ここまでで、層の完全列
を示せたことになります。つまり層の準同型 が全射、言い換えると
であるということを示せたわけです。
しかしながら、何度も注意するように、前層の準同型 が全射というわけではありません。言い換えると、
であるというわけではありません。
実際、以下の図のような包含列 を考えて、それぞれの開集合に対する
の切断を分析すると、確かに両者が異なることがわかります。

特に が穴あき円板のときに
となりますが、一方で、その層化に対する切断は
となりますね。
指数層系列のように「層の完全列が得られた」からといって、任意の開集合に対する切断のようすがすべてわかるわけではないということですね。
ここまでのまとめ
今回は指数関数 にまつわる短完全列をたくさん紹介しました。
まず、 を次の3つの準同型として解釈でき、それぞれ短完全列が構成できるのでした。
から
への準同型
から
への準同型
から
への準同型
簡単なところからスタートして、最終的にはだいぶ高度なところまで辿り着きましたが、すべてがパラレルに進んでいるのが面白いですね。
今回書いていて思ったのは、指数層系列は教育的に良さそうだということです。層の理論を勉強するにあたっても、やはり具体的な射や完全性を考えた方が理解が進むと思うのですが、その意味で指数層系列はちょうどよい例題になっていると思いました。
次回は、層係数コホモロジーを定義して、指数層系列の応用を一つ紹介しようと思います。これがわかると「指数層系列のような短完全列がいかに嬉しいか」が理解できるかもしれません。
それでは今日はこの辺で。
参考文献
基本的に今回の記事の内容はこちらの本の第4章を参考にしています。
そのため、私の内容で不明な点がありましたら、私の記述で悩むよりも、まずはこちらの本を読んでいただいた方がよいかと思います。
今回はわかりやすさを優先して 上の層として考えました。一方で、指数層系列自体は、一般のリーマン面
上でも成立します。リーマン面とは、座標が複素数になるような1次元複素多様体のことですが、座標を使うことで今回と同様に議論できるというわけです。上の本でもリーマン面上で議論されています(指数層系列は第4章の演習問題になっています)。今回の記事では
として考えたということですね。
ただ、少しだけ注意を要するところがあって、特に層の完全性の定義において「 の普遍性」を使っているあたりの議論で、若干の誤植があるような気がしています(誤解だったらすみません)。私の記事では、その点について多少変更を加えた内容を記載しています。
*1:私はここで引っかかって理解に時間がかかりました。
