ご無沙汰しております。約3ヶ月ぶりの投稿です。
4月より職場がかわったのですが、仕事に慣れるまでに期間がかかってしまい、ブログの更新が滞っておりました。その間も日曜数学は楽しく続けておりましたので、少しずつブログの方でも公開していけたらと思います。
久しぶりの記事のテーマは「フェルマーの小定理」です。フェルマーの小定理と言っても、よく知られるような数論的なものではなく、群論的 なフェルマーの小定理の類似物です。実は、フェルマーの小定理は群論的にも考えることができるんです。しかも、その証明の方法が巧妙で面白い。
今回の記事は、群論をちょっとだけかじったことがある、少し前の私のような人を想定した記事です。知らない人にはちょっと難しいかもしれませんが、雰囲気だけ追ってもらって、数学的な発想の面白さを共感してもらえたら嬉しいです。
なお今回の記事では、テーマがフェルマーの小定理ということもあって、素数が多々登場します。 という記号はすべて、素数を表すためだけに用いたいと思います。
数論的なフェルマーの小定理
まずは、フェルマーの小定理の基本形から復習しましょう。
フェルマーの小定理は
ことを主張する定理です。私のブログでも度々登場しています。基本的かつ便利な定理です。
tsujimotter.hatenablog.com
証明はそれほど難しくありませんので、やってみましょう。
まず を、すべて
倍した集合を考えます。
これらは においては元の集合と一致するはずです。なぜなら、もし一致しないのであれば
となるような の組が存在するはずですが、
の
における逆元
をかけると
となってしまい、 と矛盾するからです。
において
と互いに素な
に逆元が存在することは、以下のように示すことができます。
を満たすような整数 が存在する.
をとると,
となって, の
における逆元
の存在が示せた.
さて、先の2つの集合が で一致するということは、それらの元すべてを掛け合わせても合同関係が成り立つということです。よって、以下の合同式が得られます。
ここで
の逆元を両辺にかけると
となり、フェルマーの小定理が得られました。
 からの見方
からの見方
次に、このフェルマーの小定理を群論的に捉え直すことを試みましょう。そのための準備として「 で合同な元をあつめた集合」を用意します。
このような集合を( を法とする)
の 剰余類 といいます。以下では、この剰余類を使った2つの集合を準備します。
1つめは「 を法とする剰余類すべて」をあつめた集合です。このような集合を
と表します(読み方は「ゼットオーバーピーゼット」)。すべての剰余類を集めると言っても、無限集合にはなりません。なぜなら、
のように一致する剰余類同士が「つぶれてしまう」からです。
結局、独立な剰余類は の
個で
となります。
2つめに用意するのは「 のうち、
と互いに素な剰余類のみ」をあつめた集合です。これを
と表記することにします(読み方は「ゼットオーバーピーゼットバツ」*1)。右肩の
は「積の記号」だと思ってください。
実際そのような剰余類は、 においては「
以外のすべての剰余類」です。したがって
となります。
剰余類はそれぞれ集合ですが、これらの間にも、通常の数のような「和」と「積」を考えることができます。例を挙げると
のような感じです。
このように演算を定義すると、 が「積」に対して群をなすことがわかります*2。
さて、このような準備をしておくと、フェルマーの小定理は次のように言い換えることができます。
「なぜわざわざ、このようなまどろっこしい言い換えをするのか?」と思ったかもしれません。この言い換えは、これから述べる一般化のための布石です。
よーく観察すると、一般の群に対しても似たような命題を考えることができそうです。
は群をなす (
を一般の群
に置き換えれそう)
は 群
の任意の元 (
に置き換えれそう)
- 指数の肩の
は 群
の要素数 (
に置き換えれそう)
- 右辺の
は 群
の単位元 (
を単位元
に置き換えれそう)
これらの考察に基づいて以下が予想されます。実際、この予想は真であり、これこそが今回のテーマである「群論的なフェルマーの小定理」です。
ただし, は
の単位元.
を有限の要素を持つ群(有限群)に限定していますが、それは無限の群を考えてしまうと
が整数とならないためです。以下、この記事では群は有限群のみを扱うことにします。
それでは「群論的なフェルマーの小定理」の証明にチャレンジしたいと思います。ただし、冒頭で述べたような数論的な証明は、そのままでは使えないことに注意してください。
「数論的なフェルマーの小定理」の証明で用いた手順を踏襲すると
のような変形をしたくなります。しかしながら、一般の群は可換ではないので こんなことはできません*3。もう少し異なるアプローチが必要です。
一般の群を考える際は 「群の公理」 に立ち戻る必要があります。すなわち、証明に使える道具は、以下に挙げる「4つの公理」だけです。
すべての
に対して,次式が成り立つ (演算が閉じている)
すべての
に対して,次式が成り立つ(結合則)
単位元と呼ばれる元
が存在し,すべての元
に対して次式が成り立つ(単位元の存在)
すべての
に対して,次式を満たす逆元
が存在する (逆元の存在)
さて、使える武器はこれだけです。一体どうやって証明していくのでしょう。
以下で紹介する方法は、群の公理に基づく抽象的な証明です。でも、だからこそ面白い。この感覚をぜひ味わっていただきたいです。
証明の概略
それでは群の公理を使って、群論的なフェルマーの小定理を示していきましょう。証明までは全部で 4ステップ です。
このあとの説明では のべき乗が頻繁に登場します。
以上の整数
に対して
を以下で定義します。
以上の表記ができるのは、結合則のおかげ ということに注意してください。
結合則が成り立たない場合は、積の結合順序によって演算の結果が変わってしまい、べき乗が一意に定まりません。
また、以下では群 は常に有限群であるとします。
STEP1: 位数は有限である
まずは、群 の任意の元
に対してべき乗を考えます。実は
をべき乗していくと、いつかは必ず単位元
に一致するのです。
すなわち
を満たす正整数 が存在します。このような最小の
を「
の位数」と呼ぶことにしましょう。
をべき乗が有限回で
に戻ることは、次のように示すことができます。
を満たすような正整数 が存在します。というのも、群
の要素の数は有限なので、
のべき乗を
の要素数より多くもってくれば、鳩ノ巣原理より、少なくとも1組は値が等しい組み合わせが存在するからです。
ここで、 の逆元
を両辺に
回掛けると、
より
とおけば、
となる正整数
の存在が示せた。
証明に「鳩ノ巣原理」を使うのが面白いですね!それでは次に進みましょう。
STEP2:  が生成する巡回群は
が生成する巡回群は  の部分群である
の部分群である
が単位元に戻るということは、
をべき乗していくと「同じ並びが繰り返される」ことになります。この繰り返し単位1つ分をまとめて、次のような
の部分集合
をつくりましょう。
この集合 が
の部分群であることは明らかです。なぜだかわかるでしょうか。
また、定義より の要素数
は、
の位数
に一致することに注意してください。
なお、この のように、たった1つの元
のべき乗によってのみ生成される群のことを巡回群といいます。重要な群なので覚えておくとよいでしょう。
STEP3: ラグランジュの定理
次に、STEP2 で作った部分群 を使って、群
を分割することを考えます。
かつ
ただし は,
のすべての元に
をかけてできた集合を表す.
上記の命題では、すべての の元は分割
のいずれかに属しており、かつ、それぞれの分割は(まったく同じものでなければ)共通部分を持たない、ということを主張しています。
このような分割を考えたとき、その分割の最小の個数 を
と書くことにします。部分群
による
の最小の分割数は、「最小」なので一意に定まります。したがって、
のような記号で表すことができるのです。
上で述べたことは、図で表現するとわかりやすいかもしれません。
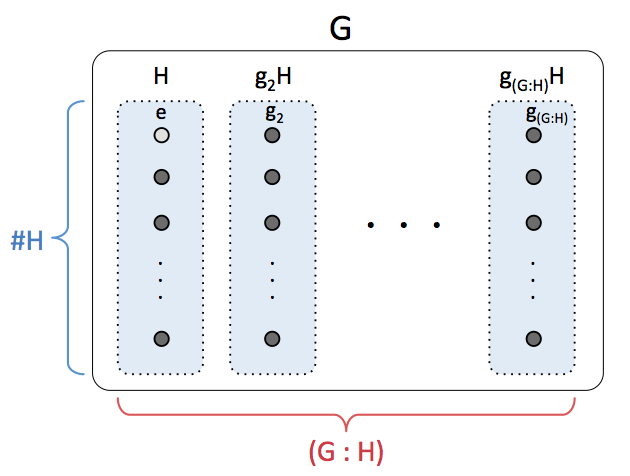
要するに「 のちょうどぴったりな分割」 が
を用いて得られるということを表しています。
図からわかるように という群の元は、縦が
個、横が
個の「長方形」に並べることができます。この長方形の面積を考えることにより、以下が成り立つことがわかるでしょう。
以上の結果により、 の位数
が
の要素数
の約数となることが、ただちにわかります。 面白いですね。
このラグランジュの定理は、もちろん群論によって証明できるのですが、ここに挟むと流れが悪くなるので記事の最後におまけとして載せたいと思います。
STEP4: 解決
仕上げです。これまでの結果を用いて、フェルマーの小定理を示しましょう。
使うのは、
一気に式変形していきましょう。
やりましたね!これにて目的の
が証明できました!
まとめ
いかがだったでしょうか。今回は群論の道具を用いて、フェルマーの小定理を一般化した定理を証明しました。
証明の手順を簡単にまとめると
の位数の存在を保証する
の生成する巡回群が,
の部分群
であることを示す
を
で割った集合の大きさから
と
の間の要素数の関係を導く(ラグランジュの定理)
というものでした。なかなかトリッキーで面白いですよね!
群論の面白さの1つに、具体的な群を考えることなく4つの公理のみで議論を進められることがあると思います。慣れてくると、抽象的で何の縛りもないようにみえた4つの公理が、思いのほか「きつい条件」であったことに気づきます。このきつい条件によって、「ラグランジュの定理」や「フェルマーの小定理」のような、まったく自明でない事実が一般的に証明できてしまうわけです。すごい!
それでは、今日はこの辺で。
長々と読んでくださってありがとうございました!
おまけ:ラグランジュの定理の証明
ラグランジュの定理において証明すべきことは、以下の2つです。
まず示したいのは
です。 これは簡単です。
もし であるなら,相異なる
で
となる組が存在するはずです.一方で,両辺に
をかけると,
となってしまい,これは矛盾します.
よって, となるほかありません.
これによって を分割していた
のすべてが、同じ要素数を持つ の部分集合であることがわかりました。上の図でいうと「縦の長さが揃うこと」が示せたことになります。
2つめに示すのは
です。これは対偶をとって考えましょう。
ここで,両辺に の逆元
を右からかける.
上式は, が
の元であることを意味している.
に
をかけると,
となるが,これは の任意の元が
の元となったことを意味している.したがって,
一方で,元の式の両辺に の逆元
を右からかける.
こちらは, が
の元であることを意味している.
に
をかけると,
となるが,これは の任意の元が
の元となったことを意味している.したがって,
以上より, であることがわかった.
これにより、すべての分割 は、他の分割
と一致しない限り共通部分をもたない、ということがわかりました。
関連記事
フェルマーの最終定理のクンマーによる解法を紹介した記事ですが,肝心なところで今回証明したフェルマーの小定理を用います( とする)。イデアル類群の位数(類数という)が重要になるのは、この定理のおかげですね。
tsujimotter.hatenablog.com
RSA暗号の記事です。キーポイントで「オイラーの定理(今回の定理の系で としたもの)」が出てきます。
tsujimotter.hatenablog.com
