FLTとクンマーとイデアル類群

2016年が始まりました。日曜数学者の tsujimotter は、今年も楽しく数学をしていきたいと思っています。どうぞよろしくおつきあいください。

というわけで、新年一発目の数学の話を。

今日の目標は、以下の命題の一般的な証明方法についての解説です。

命題：
$3$ 以上の素数 $p$ に対して，
$x^p + y^p = z^p$
を満たす整数解 $(x, y, z)$ で， $p \not\mid xyz$ であるものは存在しない．

これは、フェルマーの最終定理のファーストケースと呼ばれる命題です。 $p \mid xyz$ の場合を、セカンドケースといいますが、~~これはやや煩雑な~~かなり難しいので今日はやめておきましょう。

また、今後たくさん「フェルマーの最終定理」という言葉が出てくるので、これを $FLT$ と略すことにします。Fermat's Last Theorem の略で $FLT$ です。また、素数 $p$ に対しての $FLT$ を $FLT(p)$ と呼ぶことにしましょう。

「え？ $FLT$ の証明って、めっちゃ難しいんじゃないの？」と思った方は、この手の話をよくご存知の方ですね。一般の $p$ についての $FLT(p)$ は、1995年にアンドリュー・ワイルズによって、楕円曲線や保形形式などの高度に洗練された理論を用いて解決されたわけです。

一方「 $p$ は正則素数」という条件に限定して考えれば、話は変わります。この場合の $FLT(p)$ は、代数的な方法を使って（楕円曲線や保形形式を使わないで）証明することができるのです。

そのことを示したのが、タイトルに挙げたエルンスト・クンマーという数学者です。彼が条件として設定した「正則素数」は、イデアル類群を使って以下のように定義されます。

定義（正則素数）：
素数 $p$ について，円分体 $K = \mathbb{Q}(\zeta_{p})$ のイデアル類群 $\mathcal{C}_K$ の位数 $h_K$ を $p$ が割り切らないとき，その $p$ を正則素数という．

私が初めてこの話を聞いたときには「 $FLT$ にイデアル類群の位数がどう関係するのか」まったく想像がつきませんでした。「クンマーがイデアルを使って解決した」というエピソードは、よく通俗書に載っているので、話として聞いた方は多いかと思うのです。一方でその原理、すなわち、イデアル類群の位数との関係を理解している人はどれだけいるでしょうか。

９月ごろにせきゅーんさんという方とお会いして、その際にクンマーのアイデアについて教えていただきました。そのアイデアに大変感動しまして、すぐにでも記事にしようと思っていたのですが、なかなか手が回らずしばらく放置していたのでした。

そのせきゅーんさんが、最近、ご自身のブログで正則素数について語っています。
integers.hatenablog.com

このビッグウェーブに乗るしかないと思い、大晦日の夜に筆をとったのでした。宿題を解決するときがきたようです。結果的には、公開は正月になってしまいました。

ちょっと長い記事になりますが、アイデアは非常に面白いので、ぜひお付き合いください。

FLTに対するアプローチ

$FLT$ への最初のアプローチは，フェルマー自身によるものです。 $FLT(4)$ についての証明でした。フェルマーが用いたのは、彼のお家芸ともいえる「無限降下法」と呼ばれる方法です。

奇素数について最初に成果を挙げたのはオイラーで、 $FLT(3)$ について解決しました。クンマーの方法も、オイラーの証明法の延長線上にあるので、まずは $FLT(3)$ について解説しましょう。

$p = 3$ とします。ここで、

$x^3 + y^3 = z^3 \tag{1}$

を満たす整数解 $(x, y, z)$ で $p \not\mid xyz$ であるものは存在しないことを示します。

上式の左辺を $\mathbb{Q}(\zeta_3)$ の範囲で因数分解しましょう。ここで、 $\zeta_3$ は $1$ の原始三乗根です。

$x^3 + y^3 = (x + y)(x+ \zeta_3 y)(x + \zeta_3^2 y)$

この式の右辺は $\mathbb{Q}(\zeta_3)$ における３つの元 $x + y, \; x+ \zeta_3 y, \; x + \zeta_3^2 y$ の積の形になっています。

式 $(1)$ に代入すると、こうなります。

$(x + y)(x+ \zeta_3 y)(x + \zeta_3^2 y) = z^3$

$x + y, \; x+ \zeta_3 y, \; x + \zeta_3^2 y$ の３元が互いに素であると仮定すると、 $\mathbb{Q}(\zeta_3)$ における素因数分解の一意性から、 $x + y, \; x+ \zeta_3 y, \; x + \zeta_3^2 y$ はいずれも３乗数であることがわかります。

したがって、 $\mathbb{Q}(\zeta_3)$ の元、 $u_1+\zeta_3 v_1, \; u_2+\zeta_3 v_2, \; u_3 + \zeta_3 v_3$ を用いて以下の式が得られます。

$\begin{matrix} x+y &=& \varepsilon_1 (u_1+\zeta_3 v_1)^3 \\ x+ \zeta_{3} y &=& \varepsilon_2 (u_2+\zeta_3 v_2)^3 \\ x+ \zeta_{3}^2 y &=& \varepsilon_3 (u_3+\zeta_3 v_3)^3 \end{matrix}$

ただし、 $\varepsilon_1, \; \varepsilon_2, \; \varepsilon_3$ は $\mathbb{Q}(\zeta_3)$ 上の単数です。

あとは、こんな式を満たすような整数 $u_1, v_1, u_2, v_2, u_3, v_3$ が存在しないことを示せば、 $FLT(3)$ が解決します。

＊　＊　＊　＊　＊

オイラーの方法の延長線上で、一般の $p$ に対して $\mathbb{Q}(\zeta_p)$ 上で因数分解することにより、一般の $p$ について $FLT(p)$ が証明できるように考えるかもしれません。

すなわち、

$x^p + y^p = z^p \tag{2}$

に対して、

$(x + y)(x + \zeta_p y)(x + \zeta_p^2 y) \cdots (x + \zeta_p^{p-1} y) = z^p$

のように分解すれば、左辺のそれぞれの元が $p$ 乗数であることがわかります。これを使って $FLT(3)$ と同様の手順で証明するのです。

ラメという数学者が、上記の方法を思いついて「フェルマーの最終定理の完全解決」を宣言したこともありました。ほぼ同時期にコーシーという数学者も、同様の宣言をして、先取権をラメと争ったというエピソードは有名です。

しかしながら、上記の方法では不十分であることが後から分かりました。そのことを最初に示唆したのはリウヴィルですが、とどめを刺したのはクンマーです。

彼らは「 $\mathbb{Q}(\zeta_p)$ における素因数分解の一意性は、 $p$ によっては成り立たない場合がある」ということを指摘したのです。前述のオイラーの証明は、素因数分解の一意性を前提としていましたから、これが成り立たないと話になりません。

$p = 3$ においては、たまたま素因数分解の一意性が成り立ちます。初めてその一意性が崩れるのは、 $p = 23$ のときです。実際、 $\mathbb{Q}(\zeta_{23})$ においては、 $6$ という元は、以下のように２通りの方法で素因数分解されてしまいます。

$\begin{matrix} 6 &=& 2\times 3 \\ &=& (\zeta_{23} +\zeta_{23}^4+\zeta_{23}^9+\zeta_{23}^{16}+\zeta_{23}^2+\zeta_{23}^{13}+\zeta_{23}^{3}+\zeta_{23}^{18}+\zeta_{23}^{12}+\zeta_{23}^{8}+\zeta_{23}^{6}) \\ &&\times (\zeta_{23}^{22} +\zeta_{23}^{19}+\zeta_{23}^{14}+\zeta_{23}^{7}+\zeta_{23}^{21}+\zeta_{23}^{10}+\zeta_{23}^{20}+\zeta_{23}^{5}+\zeta_{23}^{11}+\zeta_{23}^{15}+\zeta_{23}^{17}) \end{matrix}$

この例は tsujimotter が考えたものですが、見つけるのにはなかなか骨が折れました。

さぁ、困りました。素因数分解の一意性が使えないと、オイラーの方法の応用では解決できません。どうしたらよいのでしょう。

ここで颯爽と表れたのが、本日の主役エルンスト・クンマーです。クンマーは、失敗の原因は、数をそのまま考えているからだということに気づきました。数をもっと根源的な「イデアルのレベルまで分解する」ことで「素因数分解の一意性が復活する」と主張したのです。*1

クンマーはこのような考えをもとに、一般の $p$ に対する $FLT(p)$ に挑みました。クンマーのアイデアを説明するための準備として、まずはイデアルとイデアル類群について話しておかねばなりません。

準備１：イデアル

クンマーが使ったのは、イデアルとイデアル類群という道具です。これらについては、過去に解説したこともありましたが（これとかこれとか）、この問題に合わせて改めて解説したいと思います。

注：はじめに断っておきますが、いつもの記事と比べて、この節と次の節の内容は、相当に難しい内容を含んでいます。しかも、文量の都合から、かなりすっ飛ばして書いています。そのため、ところどころ不正確な部分を含んでいることをご了承ください。
また、代数的整数論に慣れている人にとっては、退屈な話が続くかもしれません。そんな方は「クンマーのアイデア」まで飛んでいただければと思います。

まず、イデアルとは、簡単に言ってしまうと倍数の集合です。 $K = \mathbb{Q}(\zeta_p)$ の整数環 $\mathcal{O}_K$ を考えたときに、 $\mathcal{O}_K$ のイデアルは以下のように定義されます。

$(\alpha_1, \alpha_2, \ldots, \alpha_m) = \{ \alpha_1 \xi_1 + \alpha_2 \xi_2 + \cdots + \alpha_m \xi_m \mid \xi_1, \xi_2, \ldots, \xi_m \in \mathcal{O}_K \}$

これを、 $\alpha_1, \alpha_2, \ldots, \alpha_m$ で生成される $\mathcal{O}_K$ のイデアルと呼ぶことにします。 $m$ は任意の正整数です。 $m = 1$ の場合に、特別に単項イデアルと呼びます。

$(\alpha) = \{ \alpha \xi \mid \xi \in \mathcal{O}_K \}$

この単項イデアルが重要です。単項イデアル $(\alpha)$ は、まさに $\alpha$ の倍数ですね。

さてこのイデアルには、積が定義できます。

たとえば単項イデアル同士に対しては、単純な積と同じような計算となります。

$(\alpha)(\beta) = (\alpha \beta)$

２つの元によって生成されるイデアルに対してもこのように積を計算します。

$(\alpha_1, \alpha_2)(\beta_1, \beta_2) = (\alpha_1 \beta_1, \alpha_2 \beta_1, \alpha_1 \beta_2, \alpha_2 \beta_2)$

もう１つ例を挙げておきましょう。

$(\alpha)(\beta_1, \beta_2, \beta_3) = (\alpha \beta_1, \alpha \beta_2, \alpha \beta_3)$

一般のケースは推して知るべしですね。

このままでは、積を計算するたびにどんどんイデアルの生成元が増えていってしまって、困りますね。

実は、ユークリッドの互除法が使えるときは、必ずしもこんなに生成元は必要ないことがわかります。ユークリッドの互除法によると、 $\alpha, \beta$ の最大公約数が存在して $\delta$ と表されるとき、任意の $\xi \in \mathcal{O}_K$ に対して、以下の式をみたす $\xi_1, \xi_2 \in \mathcal{O}_K$ が存在します。

$\alpha \xi_1 + \beta \xi_2 = \delta \xi$

よって、このような $\alpha, \beta$ によって生成されるイデアルは、以下のように変形できることがわかります。

$(\alpha, \beta) = \{ \alpha \xi_1 + \beta \xi_2 \mid \xi_1, \xi_2 \in \mathcal{O}_K \} = \{ \delta \xi \mid \xi \in \mathcal{O}_K \} = (\delta)$

最大公約数が存在する場合には、生成元が一つになり、単項イデアルになりましたね。

整数環によっては、すべてのイデアルが単項イデアルになってしまうものが存在します。このような環を単項イデアル環といいます。 $K$ の整数環 $\mathcal{O}_K$ が単項イデアル環であれば、 $K$ において素因数分解の一意性が成り立つことが知られています。これは重要な事実なので、覚えておいてください。

単項イデアルの重要性について、もう少しだけ触れておきましょう。

$\alpha, \beta$ の２つの元でそれぞれ生成される２つの単項イデアルが、

$(\alpha) = (\beta)$

のような等式を満たすとき、以下が成り立ちます。

$\alpha = \varepsilon \beta$

$\varepsilon$ は単数です。すなわち、単項イデアルの間の等号は、その生成元の等号と（単数を除けば）一致します。このことは、単項イデアルはその生成元と同等に扱えるということです。

単項イデアルをどうにかして作ってあげれば、数の計算に持ち込める、という方針が今後重要になります。

また、最初に述べたように「すべてのイデアルは素イデアルの積に一意に分解できる」という重要な事実があります。
すなわち、任意のイデアル $A$ に対して、素イデアル $P_1, P_2, \ldots, P_k$ が存在し、

$A = P_1^{e_1} P_2^{e_2} \cdots P_k^{e_k}$

というように一意に表現できるのです。

$K = \mathbb{Q}(\zeta_{23})$ の例で考えると、 $(6)$ という単項イデアルは以下のように分解できます。

$(6) = (2)(3) = (\xi_1)(\xi_2)$

ただし、

$\xi_1 = \zeta_{23} +\zeta_{23}^4+\zeta_{23}^9+\zeta_{23}^{16}+\zeta_{23}^2+\zeta_{23}^{13}+\zeta_{23}^{3}+\zeta_{23}^{18}+\zeta_{23}^{12}+\zeta_{23}^{8}+\zeta_{23}^{6}$

$\xi_2 = \zeta_{23}^{22} +\zeta_{23}^{19}+\zeta_{23}^{14}+\zeta_{23}^{7}+\zeta_{23}^{21}+\zeta_{23}^{10}+\zeta_{23}^{20}+\zeta_{23}^{5}+\zeta_{23}^{11}+\zeta_{23}^{15}+\zeta_{23}^{17}$

です。

さらに、 $(2), (3), (\xi_1), (\xi_2)$ は、イデアル $A, B, C, D$ を用いて「もっと深く」分解できます。

$(2) = A B$

$(3) = C D$

$(\xi_1) = A C$

$(\xi_2) = B D$

したがって、結局、

$(6) = ABCD$

となります。これが一意な素因数分解というわけですね。

残念ながら、 $A, B, C, D$ は扱いやすい単項イデアルにはなりませんが、この際仕方ありません。別の方法を使ってなんとか処理しましょう。

準備２：イデアル類群

次に、イデアル類群について述べたいと思います。

その前に、分数イデアルについて話しておきます。 $K$ の分数イデアルとは、 $(0)$ を除く $\mathcal{O}_K$ のイデアル $A$ と、 $0$ を除く $K$ の元 $\alpha$ を用いて、以下のように定義されます。

$\alpha A = \{ \alpha \gamma \mid \gamma \in A \}$

単項分数イデアルも定義できます。 $K$ の単項分数イデアルは、 $0$ を除く $K$ の元 $\alpha$ を用いて、以下のように定義されます。

$(\alpha) = \alpha (1) = \{ \alpha \xi \mid \xi \in (1) \}$

前の節で定義したイデアルは「整数的な存在」だったわけですが、これを整イデアルと呼びます。分数イデアルは、整イデアルに $\alpha$ という $K$ の元をかけています。 $\alpha$ は「有理数的な元」と見れば、「整イデアルの分数バージョン」と想像つくと思います。整数と分数の違いは「割り算」です。すなわち、積の逆元が定義できるわけです。

整イデアル $A, B$ を用いて $I = \alpha A, \; J = \beta B$ と表せるような、分数イデアル $I, J$ に対して、積を以下のように定義します。

$I J = (\alpha \beta) AB$

こうすると、 $I$ の逆元 $I^{-1}$ を考えることができます。整イデアル $A$ にかけると単項イデアルになるような整イデアル $A'$ を考えて、これらの積が $AA' = (\gamma)$ となるとする。これを使って、逆元を以下のように定義します。

$\displaystyle I^{-1} = \frac{1}{\alpha \gamma} A'$

このように定義すると、

$\displaystyle I I^{-1} = \alpha A \frac{1}{\alpha \gamma} A' = \frac{\alpha}{\alpha \gamma}AA' = \frac{1}{ \gamma}(\gamma) = (1)$

となって、確かに逆元になっていることがわかります。

さて、こうしてできた分数イデアル全体の集合を $\mathcal{J}_K$ としましょう。この集合は、上で定義した積に対し、結合則・交換則を満たします。また、単位元が存在し、任意の元に対して逆元を持ちます。したがって、 $\mathcal{J}_K$ はアーベル群を成します。

さらに、単項イデアル全体の集合を $\mathcal{P}_K$ とすると、これもアーベル群を成します。また、 $\mathcal{P}_K$ は定義より $\mathcal{J}_K$ の部分群ですね。アーベル群の任意の部分群は正規部分群なので、 $\mathcal{P}_K$ は $\mathcal{J}_K$ の正規部分群です。

正規部分群があれば、商群を作りたくなります。それを次のように表しましょう。

$\mathcal{C}_K = \mathcal{J}_K \big/ \mathcal{P}_K$

これこそが、イデアル類群です。

イデアル類群の位数は、有限であることがわかります。これが、類数 $h_K$ と呼ばれる数で、この類数が鍵なのでした。

はぁー長かった。
定義するだけで、こんなに説明が必要なんて。

さて、このイデアル類群のイメージをつかむことが、肝心なわけです。

たとえば、 $K = \mathbb{Q}(\zeta_{23})$ においては、類数が $h_K = 3$ でイデアル類群 $\mathcal{C}_K$ は３次の巡回群になります。この場合 $\mathcal{C}_K$ は、単項分数イデアルでない分数イデアル $P$ を使って、以下のように表せます。

$\mathcal{C}_K = \mathcal{J}_K \big/ \mathcal{P}_K = \{ \mathcal{P}_K, P\mathcal{P}_K, P^2\mathcal{P}_K\}$

図に表すとこんな感じです。

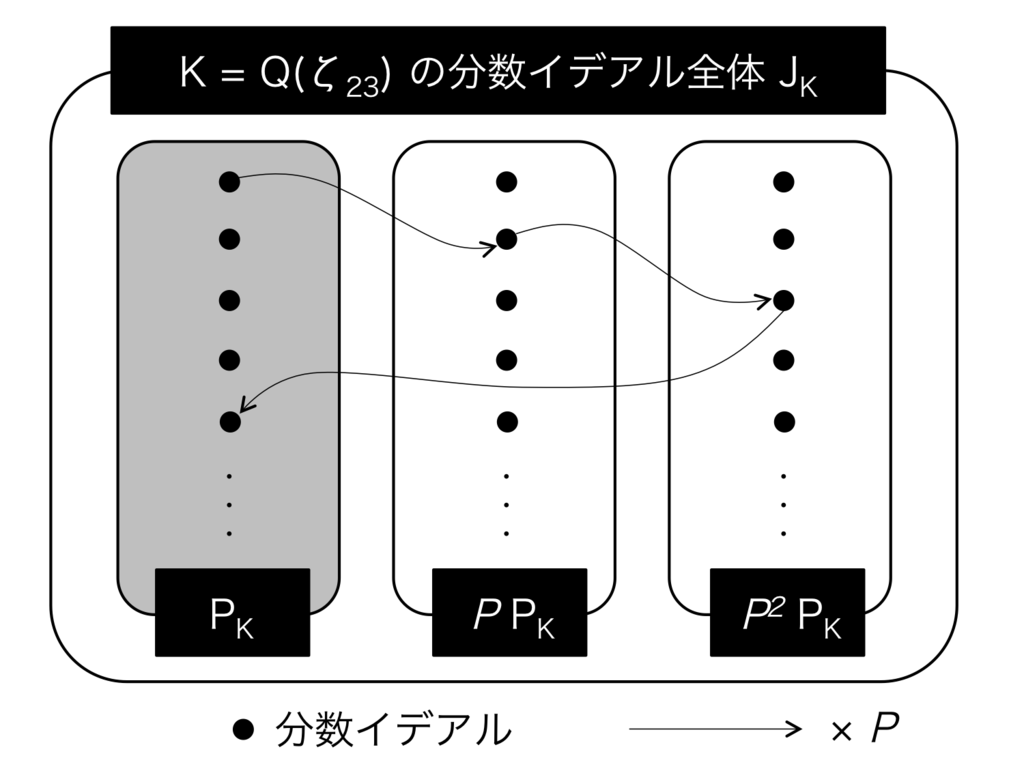
f:id:tsujimotter:20160101011235p:plain:w400

単項分数イデアルの集合 $\mathcal{P}_K$ に属するイデアルは、 $P$ をかけると $P\mathcal{P}_K$ に属する分数イデアルになります。また、 $P\mathcal{P}_K$ に属する分数イデアルは $P$ をかけると、 $P^2\mathcal{P}_K$ に属する分数イデアルになります。さらに $P$ をかけると、単項分数イデアルに戻ってきます。 $P\mathcal{P}_K, P^2\mathcal{P}_K$ に属する分数イデアルは、単項分数イデアルではありませんが、それぞれ $P^2, \; P$ をかけてあげれば、単項分数イデアルに戻ります。

すなわち、イデアル類群は、それぞれの分数イデアルが単項分数イデアルからどれぐらい離れているのかを、具体的に表している群であるといえるわけです。

さて、ようやく準備が整いました。イデアルとイデアル類群という武器を持って、クンマーのアイデアに迫っていきましょう。

クンマーのアイデア

ようやくクンマーの方法の登場です。

まずは、ラメがやったように

$x^p + y^p = z^p \tag{2再掲}$

という式を、

$(x + y)(x + \zeta_p y)(x + \zeta_p^2 y) \cdots (x + \zeta_p^{p-1} y) = z^p$

のように分解しましょう。

そして、左辺の積のそれぞれの元と右辺の $z$ を、単項イデアルとして考えましょう。すると、以下の等式が成り立ちますね。

$(x + y)(x + \zeta_p y)(x + \zeta_p^2 y) \cdots (x + \zeta_p^{p-1} y) = (z)^p$

さぁ、ここで $(z)$ という単項イデアルの素因数分解を考えましょう。イデアルは一意に分解できるのでしたね。

$(x + y), (x + \zeta_p y), \ldots, (x + \zeta_p^{p-1} y)$ が互いに素であると仮定すると、素イデアル分解の一意性より、これらはイデアルの $p$ 乗の形で表せることがわかります。

したがって、 $\mathcal{O}_K$ のイデアル $A_0, A_1, \ldots, A_{p-1}$ を用いて、以下のように表せます。

$(x+y) = A_0^p$

$(x+\zeta_p y) = A_1^p$

$\vdots$

$(x+\zeta_p^k y) = A_k^p$

$\vdots$

$(x+\zeta_p^{p-1} y) = A_{p-1}^p$

全部扱うと面倒なので、代表して $k$ について考えましょう。 $k = 0, 1, 2, \ldots, p-1$ です。

$(x+\zeta_p^k y) = A_k^p \tag{3}$

ここで、もし $A_k$ が単項イデアルだったなら（そんな都合のいいことがあれば）、 $A_k = (\alpha_k)$ とおいて（ $\alpha_k$ は $\mathbb{Q}(\zeta_p)$ の整元）

$(x+\zeta_p^k y) = (\alpha_k)^p$

と表せます。したがって、両辺単項イデアルなので、単数 $\varepsilon$ を用いて

$x+\zeta_p^k y = \varepsilon \alpha_k^p$

と表すことができます。やったね、これでオイラーの方法と同じ結論が得られました。

では、 $A_k$ が単項イデアルであるなんていう、そんな都合のいいことがあるんでしょうか。 $p$ が正則素数のときに限っては、そんな都合のいいことがあるんです。

ここからが、一番面白いところなので落ち着いてよく聞いてください。

まず、イデアル類群 $\mathcal{C}_K$ の任意の元は、イデアル類群の位数 $h_K$ 乗すると単位元に戻ります。これは群論におけるフェルマーの小定理です。つまり、 $\mathcal{C}_K$ における $A_k$ の属する類を $[A_k]$ とすると、以下が成り立ちます。

$[A_k]^{h_K} = \mathcal{P}_K \tag{4}$

$\mathcal{C}_K$ の単位元は、単項イデアルの属する類 $\mathcal{P}_K$ ですね。

一方 $(3)$ 式より、 $A_k^p$ は単項イデアルです。したがって、

$[A_k]^{p} = \mathcal{P}_K \tag{5}$

となるでしょう。

さぁここで、 $p$ が正則素数なら、すなわち $p$ が $h_K$ を割り切らないのであれば、 $p$ と $h_K$ は互いに素です。互いに素な２整数に対しては、ユークリッドの互除法より、

$ap + bh_K = 1$

となるような整数 $a, b$ が存在します。よって、

$[A_k]^{ap + bh_K} = [A_k]^1 \tag{6}$

が成り立ちます。

$(4), (5)$ を $(6)$ 式に代入することにより、

$[A_k] = \mathcal{P}_K \tag{6}$

が得られます。すなわち、 $A_k$ が単項イデアルであることがわかりました！！！

「 $p$ が $h_K$ を割り切らない」という正則素数の条件は、「 $p$ と $h_K$ が互いに素」すなわち、ユークリッドの互除法を使うための条件だったのですね！これは面白い！

「割り切らない」という一見ネガティブな条件が、こんなにもきれいに使えてしまうのですね。逆に「 $p$ が $h_K$ を割り切る」という条件では、同じような論法は使えないことは明らかです。このような素数 $p$ は、非正則素数と呼ばれています。非正則素数に対しては、クンマーのアプローチは使えないわけですね。

正則素数ってどんな数？

クンマーのアプローチはわかったわけですが、具体的にこの方法が使えるケース、すなわち、正則素数はいったいどんな数なのでしょうか。

それは、円分体 $K = \mathbb{Q}(\zeta_p)$ の類数 $h_K$ を調べればわかります。 $100$ 以下の素数について、すべて列挙してみましょう。

$p$	$h_K$	$h_K$ の素因数分解	正則 or 非正則
$3$	$1$	$1$	正則素数
$5$	$1$	$1$	正則素数
$7$	$1$	$1$	正則素数
$11$	$1$	$1$	正則素数
$13$	$1$	$1$	正則素数
$17$	$1$	$1$	正則素数
$19$	$1$	$1$	正則素数
$23$	$3$	$3$	正則素数
$29$	$8$	$2^3$	正則素数
$31$	$9$	$3^2$	正則素数
$37$	$37$	$37$	非正則素数
$41$	$121$	$11^2$	正則素数
$43$	$211$	$211$	正則素数
$47$	$695$	$5\times 139$	正則素数
$53$	$4889$	$4889$	正則素数
$59$	$41241$	$3\times$ $59$ $\times 233$	非正則素数
$61$	$76301$	$41 \times 1861$	正則素数
$67$	$853513$	$67$ $\times 12739$	非正則素数
$71$	$3882809$	$7^2 \times 79241$	正則素数
$73$	$11957417$	$89 \times 134353$	正則素数
$79$	$100146415$	$5 \times 53 \times 377911$	正則素数
$83$	$838216959$	$3 \times 279405653$	正則素数
$89$	$13379363737$	$113 \times 118401449$	正則素数
$97$	$411322824001$	$577 \times 3457 \times 206209$	正則素数

類数の値は、英語版 Wikipedia の "Cyclotomic field" の記事を参考にしました。（日本語版の記事には載っていません！）

Cyclotomic field - Wikipedia

以上より、 $100$ 以下の非正則素数は $37, 59, 67$ の３つだけですね。これ以外の素数 $p$ に対しては、クンマーの方法によってすべて解決することができます。

正則素数の割合は、全体の素数の 61 パーセントだと予想されているそうです*2。したがって、該当の素数 $p$ においては、クンマーの方法を使って $FLT(p)$ が解決できることになりますね。

また、 $p = 19$ 以下の素数に対しては、 $h_K = 1$ すなわち $\mathcal{O}_K$ が単項イデアル環になるようです。したがって、この表からラメの方法が使えるのは $p = 19$ までだということもわかります。

ところで、円分体の類数をわざわざ調べずとも、非正則素数を調べる方法があるそうです。クンマー自身が発見したベルヌーイ数を使う方法です。

これについてはせきゅーんさんの記事を見てもらったら早いでしょう。
integers.hatenablog.com

この方法を使うと「 $691$ が非正則素数であること」がすぐにわかります。

代数的に考えるとイデアル類群の位数から「正則素数（regular prime）」がわかり、一方でベルヌーイ数を使うと「非正則素数（irregular prime）」がわかる。いったい、どちらが本当の意味で "irregular" なんでしょうか。

まとめ

今日は、 $FLT$ に関するクンマーのアプローチについて解説しました。

「イデアル類群の位数 $h_K$ を $p$ が割り切らない」という一見どう使っていいかわからない条件を、互いに素とユークリッドの互除法を使って、「扱いやすい単項イデアルを作る」ことに見事に利用できている、という点が非常に面白く、アツいポイントだったのではないかと思います。

長々と準備が必要で、なかなか理解が大変な内容だったかと思いますが、ここまで読んでくれた方は本当にありがとうございます。

最後に宣伝ですが、今回の主役であった正則・非正則素数がリストアップされた素数Tシャツを以下のURLから買うことができます。今回の話で正則素数に愛着が湧いた方は、ぜひお買い求めください。
tmix.jp

私も買いました。笑

f:id:tsujimotter:20160101053318j:plain:w240

それでは、今日はこの辺で。本年もどうぞよろしくお願いします。

参考文献

京都大学の雪江先生の本です。せきゅーんさんから「クンマーのアイデア」で書いた内容の概略を教えてもらった後に、本屋で関連する書籍を探しているときに見つけました。第８章「代数的整数論」の定理 8.11.15 の証明部分が直接関連する箇所です。

整数論1: 初等整数論からp進数へ

作者:雪江明彦
発売日: 2013/08/02
メディア: 単行本

私の記事読まなくても「この本を見ればいいじゃん」と思う方もいるかもしれません。とはいえ、たぶん私が９月以前にこの本を手にとっていたとしても、この内容を理解できなかっただろうし、そもそもここに解決の鍵があるなんて気づかなかったと思うのです。そういう意味で、アイデアのイメージといいますか、エッセンスを指南してくれる人の存在は貴重だなと思うのです。この記事が、当時の私と同じような立場の人に対する、理解の助けになればいいなと思います。

あと、別の素数Tシャツのリンクです。
tmix.jp