保型形式の理論を勉強していると基本領域(Fundamental Domain)という概念が出てきます。これ非常に重要な概念だと思うのですが、専門書を読んでも何を書いてあるかサッパリ分からないのですよね。
これ以上考えていても埒があかないので、図示してみようと思ったのが今回のきっかけです。やってみると、意外とゲームっぽい要素があったのでゲームにしてしまえと思って、結果ゲームになりました。笑
何はともあれ、まずは遊んでみてください。
遊び方
まず上のページにアクセスします。すると、こんな画面が出るでしょう。
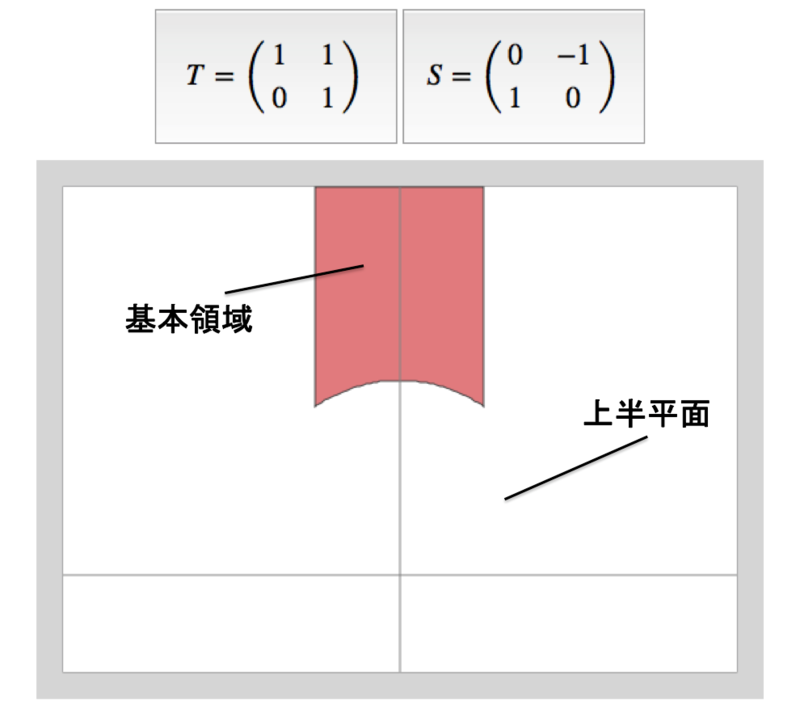
赤色の「基本領域」からスタートします。「S」と「T」という、何やら厳めしい「行列」が書かれたボタンを押していくと、ボタンに対応する領域が新たに塗られます。これを繰り返していくと、今まで白かった領域が赤色に染まっていきます。ちなみに、この塗ろうとしている目的の平面を「上半平面」といいます。
この領域を広げていき、最終的には、上半平面を一通り赤色で埋め尽くすことが目的です。
と言っても、無限に続けることができますし、とくにゲームが終了するわけではありません。満足できたら終わりです。
tsujimotter は以下のぐらいまで塗ったところで満足しました。ここまでやるのは意外と難しいのですよ。
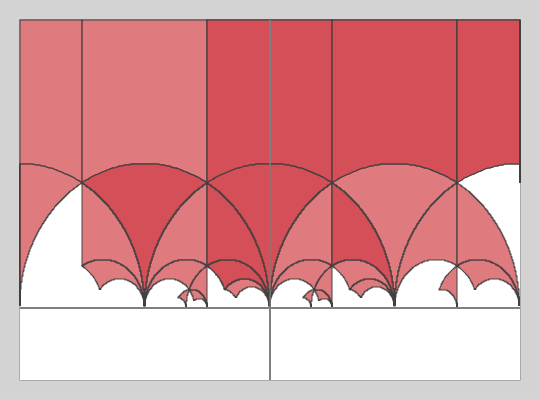
満足したら、スクリーンショットを SNS に貼って自慢してもいいでしょう。自由に遊んでみてください。
新しい遊び方、要望などを思いついた方がいましたら、@tsujimotter までご一報ください。
数学的な解説
プログラミングをしているうちにだんだんと理解が深まってきてしまいましたので、ここで数学的な背景を解説したいと思います。
まず保型形式は、前回の記事で解説したように、上半平面 上で定義される複素関数です。ずばり複素数平面の「上半分」を指している領域なので、上半平面といいます。
で、一般の保型形式の説明は抽象的すぎるので、ここでは に対する保型形式を考えます。
 に対する保型形式
に対する保型形式
は以下の式で定義される線形変換の群です。
行列の各要素が「整数」になっていること、そして、行列式が 1 であること、が際立った特徴です。
別名「フルモジュラー群」といいます。何が「フル」かというと、この部分群があってこれまた保型形式に使われるのですが、その部分群と比較して「フル」ということです。
と何度も書くのは大変なので、
と置きましょう。つまり、
ということです。(この書き方は標準的な記法で、よく使われます。)
この変換が、先ほどの上半平面上の複素数 に対して作用します。具体的にはこんな感じになります。
ただし、 。
「複素関数論」を習った方は、「一次分数変換」といえば思い出してもらえるでしょうか。
さて、フルモジュラー群 に対する保型形式(または、
に対する保型形式)とは、
を満たす 上の正則関数であり、
においても正則であるものを言います。
後半の正則性の話はさておき、前半の話は の元による変換に対して、
しか形が変化しない、ということを主張しています。「型が保たれている」わけです。そのため「保型」形式と呼びます。
基本領域のイメージ
さて、そろそろ基本領域の話にいきたいですね。そのためには (1) 式が鍵となるわけですが、この式は何を指しているのでしょう。
たとえば、 の元として、以下のものをとってきましょう。
この変換 は非常にシンプルな変換です。どういうものかは、
に作用させてみれば一目瞭然です。
これ、ただの「平行移動」ですね。そう、変換 は平行移動を表す変換行列です。
の元には、平行移動も含まれているのですね。一気に親しみが沸いてきませんか?
親しみが沸いたついでに、高校数学を思い返してみてください。 に対する保型形式は、平行移動して(ほとんど)同じ形に戻る関数です。似たような関数がありませんでしたか。
そう、三角関数です。たとえば、これはどうでしょう。
の変換に対して、同じ形に戻りますね。残念ながら、三角関数は保型形式そのものではありません。保型形式は、他の変換に対しても不変でなくてはなりませんからね。
さて、三角関数には周期がありました。上の三角関数は、基本周期は から
でしたね。高校のときもそうでしたが、本来の三角関数の定義域は、実数すべてであったにも関わらず、この基本周期の範囲しか考えませんでした。それは、基本周期だけ考えて、あとの領域は「
の変換に対する不変性」を使ってあげればよいからですね。「コピー&ペースト」できるわけです。
に対する保型形式についても、まったく同じことがいえます。複素数の範囲で、
の実部が
から
までの「基本周期」を考えて、この範囲で値を求めることが出来れば、 (1) 式の保型性からすべての上半平面においての値が「コピー&ペースト」で求まります。
保型形式が三角関数の例と異なる点は、「考えるべき領域」が基本周期よりももっと小さい範囲で済むということです。他にも、いろいろな変換があります。たとえば、こんな変換です。
この変換 は
と比べるとややイメージが難しいですが、
に作用させると以下のようになります。
このようなさまざまな変換に対する保型性を考慮して、「コピー&ペースト」するための最小限の領域は、いったいどんな領域でしょう。それが、タイトルにもある「基本領域」です。
における基本領域は、まさにゲームの最初に登場する、赤色の領域
です。
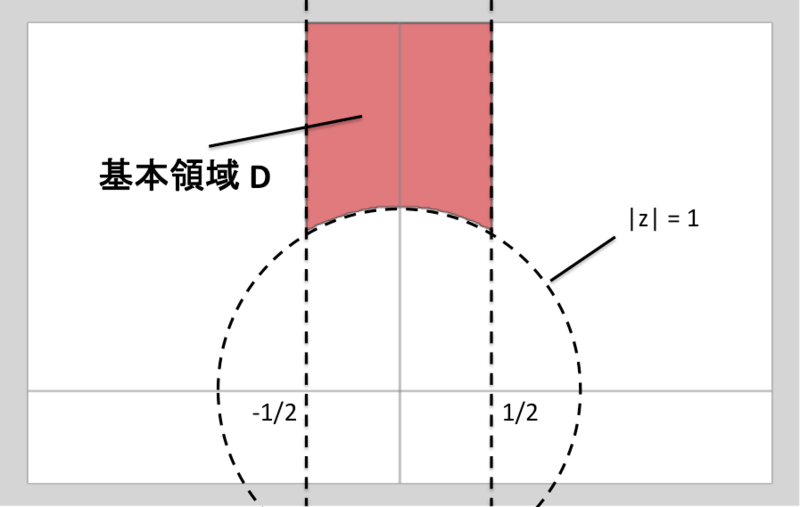
左右は の実部が
から
の範囲に収まっています。下側の扇形にくりぬかれた部分の半径は
となっています。この赤色の領域
に
の元を作用させると、
上の別の領域に移動します。
試しに、 に
を作用させてみましょう。
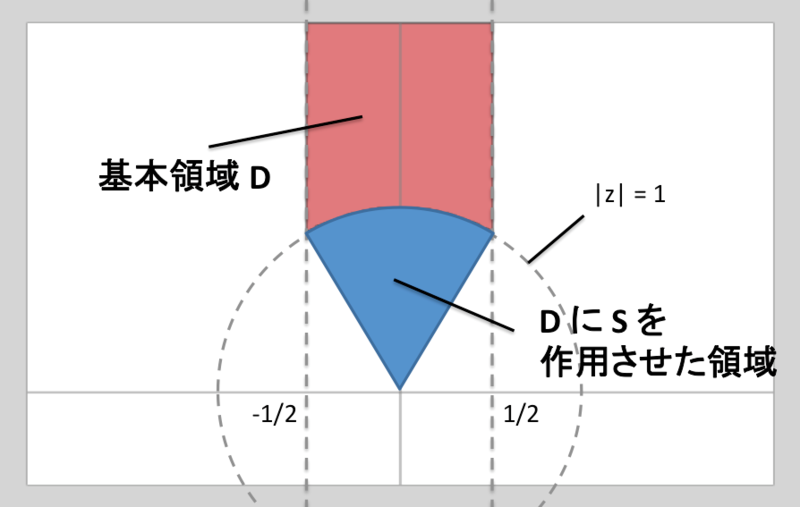
青い領域に移動しますね。 の担当する領域はここだったというわけです。
を作用させると、(明らかですが)右に平行移動します。
この作用は繰り返すことができて、 を作用させたあと
を作用させて、さらにまた
を作用させて・・・、のようなことができるわけです。
重要なことは、 は基本領域なので、
のすべての元を作用させると、
を埋め尽くすことができるということです。しかも、漏れなくダブりなく。
だからサブタイトルが「上半平面 H を埋め尽くせ!」だったわけですね。 ですべてを埋め尽くすことは、数学的に示された事実だったというわけです。面白いでしょう。
基本領域の定義
基本領域 は、数学的には以下のように定義されます。
この記法がいまいちイメージが沸かないですよね。tsujimotter もそうです。不正確なことを承知の上で、あえてイメージを説明するなら、こうでしょうか。
の部分集合である基本領域
は
のすべての元の作用によって
全体を埋め尽くします。このことを仮に
と書きましょう。この式から、逆に
のように書けそうですね。これを商集合と読んでいます。
そうなると、(2) 式で のように「バックスラッシュ」記号を使っていることが気になるかと思いますが、これは「
が左から作用することを意識した書き方」ということのようです。参考文献の 146 ページに書いてありました。
ここで
は集合
に左から作用するので,習慣的に
ではなく
という記号の方が使われている.
tsujimotter はこの記法が気になって、ずっと悩んでいたのですよ。「バックスラッシュって何やねん」と。実際はたいした話ではありませんでした。
 の生成元
の生成元
もう1つだけ、フルモジュラー群 の重要な性質について触れておきましょう。
は、なんと
というたった2つの元により生成されます。このことを数式で次のように書きます。
「2つの元により生成される」とは、2つの元を組み合わせることで、 のすべての元を表現することが出来るということです。
だから、ボタン2つで十分だったということです。
重要なことを話し終えたので、解説はこの辺りにしておきましょう。
まとめると、
- 基本領域
は、
の作用によって、上半平面
全体に「コピー&ペースト」できる。逆に、「コピー&ペースト」するための最小限の領域を基本領域と呼ぶ。
は
と
という、たった2つの元から生成される。
ということでした。
2015/04/11 訂正
「 の生成元は
の3つである」と書いていましたが、「
の2つ」の誤りでしたので訂正しました。
は単位行列
にマイナスをかけたもので、以下のように定義されます。
に作用させるとこうなります。
変換としては、単なる恒等変換ですね。
この変換行列は、以下の式のように によって表現できるため、生成元は2つで十分だと言えます。
この件は、三重積さまよりご指摘いただきました。ありがとうございます!
まとめ
みなさんはゲームを通して、「基本領域が であること」と「フルモジュラー群
は
により生成されること」を身を持って体験できたというわけです。どうでしょうこの教育効果!笑
という冗談はさておき、実際一番勉強になったのは私自身ですね。最初は、 がどんな作用をするか知りたい、という素朴な疑問から始まりました。まぁ、それぐらいほとんど理解してなかったのですよね。それが、こんなに丁寧に解説できるぐらい理解できました(つもりです)。
冒頭に述べた通り、自分で手を動かして作ってみると本当に勉強になります。
やっぱり、(情報系にとっては)プログラミングは数学理解の大きな武器である、ということを再認識いたしました。
円板バージョンも作りました!(2015/04/10夜 追記)
先ほどのゲームは,上半平面 で考えていましたが,無限に広いので全体を見渡すのが大変ですよね。
そこで,ケーリー変換と呼ばれる一次分数変換を使います。ケーリー変換を使うと,上半平面 が半径
の単位円板内の領域に全単射されるのです。ケーリー変換は次の式で記述されます。
これを応用して,表示する領域を単位円板に収めたのが以下のバージョンです。これはこれで,先ほどと違った感覚が味わえて面白いです。ぜひ触ってみてください。
(こっちの方が難度が高いように思えるのは気のせいでしょうか・・・?)
参考文献
この分野の標準的な教科書なのだと思います。通称「黄色い本」。今回のお話は、第三章に関連します。
家にたまたま置いてあって、開いてみたらちゃんと目的の解説が載っていたという本でした。非常に難しいですが、「基本領域」の説明など、よくよく読むと意外と丁寧に書いてくれています。

- 作者: N.コブリッツ,上田勝
- 出版社/メーカー: 丸善出版
- 発売日: 2012/07/17
- メディア: 単行本
- 購入: 1人 クリック: 1回
- この商品を含むブログを見る
