名古屋に行った際に,たまたま立ち寄った通りで「双曲幾何学」的な図形をいくつか見かけましたので,テンション上がって写真をパシャパシャしてしまいました!せっかくなので,ブログでもご紹介します。
双曲幾何学って?(おさらい)
双曲幾何学について,ちょっと雑な説明にはなりますが簡単におさらいしましょう。
双曲幾何学とは,ユークリッド幾何学の「第5公準(別名,平行線公準)」
1つの線分が2つの直線に交わり、同じ側の内角の和が2直角より小さいならば、この2つの直線は限りなく延長されると、2直角より小さい角のある側において交わる。
を否定することで実現する「非ユークリッド幾何学」の1つで,「双曲平面」という「ユークリッド平面(平坦な面)」とは異なる曲がった面を扱う幾何学のことです。特に双曲平面は,非ユークリッドな平面の中でも「負の定曲率を持つ」という性質で特徴付けられます。
上で説明した性質は少しわかりにくかったと思いますが,簡単にお話しすると,ある直線 を考えたときに「直線
が通らない1点を通り,かつ,直線
と交わらない2本以上の直線を引くことができる」ということです。これは,1点を通る「(直線
の)平行線」を2本以上引けるということで,ユークリッド平面ではありえなかった性質ですよね。双曲平面は一風変わった性質を持つ平面なのです。
一方で,双曲平面は我々が慣れ親しんだユークリッド平面上に「そのままでは」表すことができません。理解のためにはさまざまな工夫が必要で「(1) 高次元の空間に埋め込んだり」「(2) 縮尺を歪ませて平面に無理やり表したり」して表現されることが多いです。
これまでの数学者によって,双曲平面を表現するさまざまな「モデル」が提案されており,今回はそのうち2種類のモデルが関連します(あとで紹介します)。
ここまで簡単におさらいしたわけですが,さすがにこれだけじゃ双曲幾何学のことはなかなかイメージ出来ないですね。
というわけで,私のおすすめの本をご紹介したいと思います。
私が一番わかりやすいと感じたのはこちらの本です。この本で双曲幾何学を具体的にイメージできるようになりました。興味を持った方は是非手に取ってみてください。
さらにもう一つ。つい先日,数学ガールの新刊が発売されましたが,その第4章「非ユークリッド幾何学」にも大変分かりやすく載っています。この章の説明は,感動的にわかりやすいので,まだの方にはぜひ読んでいただきたいところです。
それでは,名古屋で見つけた双曲幾何学をご紹介します!
駅前にそびえ立つ「ベルトラミーの擬球」
「ベルトラミーの擬球」とは「負の定曲率をもつ双曲平面」を実現するモデルで,双曲平面が3次元空間に埋め込まれて表現されます。双曲幾何学の初期に発見されたものです。ガウスによって考察されていたことでも知られていますね。
Wikipediaの以下のページの右下に「擬球」の図が載っています。
ラッパを長くしたような図形ですね。「牽引線(線分を引きずってできる曲線)」を回転体にしたものです。こちらの @matsumoring さんのスライド(の27ページ以降)がわかりやすいかと思います。
たとえば,この擬球の面上での「直線」は,いわゆる「測地線」と呼ばれるものです。この擬球上では,ユークリッドの第五公準が成り立たず,1点を通る平行線を無数に引くことができます。ほかにも,この面上で三角形を描くと,三角形の内角の和を180度より小さくとることができたりします。
さて,このベルトラミーの擬球がどこにあったかというと,JR名古屋駅の目の前です。名古屋駅を桜通側から外に出て,2015年に新しくなった「大日本ビルヂング」の建物の目の前にありました。

ほんとのことを言うと,実際に擬球をモデルにしてデザインされたかどうかはわかりません。このへんはデザインした方に聞いてみたいものですね。少なくともtsujimotterには擬球に見えたというお話でした。
ついでに言うと,絡み合った線によって形作られていて,どことなく「ファイブレーション」を思わせる作りになっています(ファイブレーションよく知らないけど)。
www.youtube.com
この謎のモニュメントですが『モニュメント「飛翔」』という名前がついています。名古屋人ではないのでよく知りませんが,有名なものなのだそうです。Wikipediaの記事まであります。
Wikipediaによると,2017年現在このモニュメントは,2027年のリニア中央新幹線開業にむけて移設作業が検討されているそうです。見たい方は早めに行くのがよいかもしれません。
(2018年4月30日現在はまだありました。)
森の地下街に描かれた「ポアンカレ円板」
上のモニュメントをツイートしたところ,栄駅の近くの地下街にも,双曲幾何学に関連した図形があるぞと @alytile さん(テセレーションがご専門のタイリング大好きなお方)に教えていただきました。ちょうど,その周辺で夕食を食べ終わったところだったので*1,腹ごなしに双曲幾何学探しをすることに。
見つけるのに少し苦労したのですが,@alytile さんにいただいた写真を頼りになんとか見つけることができました!
それがこちらです!

この図形の構成を幾何学的に考えてみましょう。まず,以下のように半径の異なる2重の円を描きます。これが双曲平面のモデルである「ポアンカレ円板」です。双曲平面は,この「外側の円」の(境界を含まない)内部全体となります。あとで解説しますが,外側の円はこの平面における「世界の果て」になります。
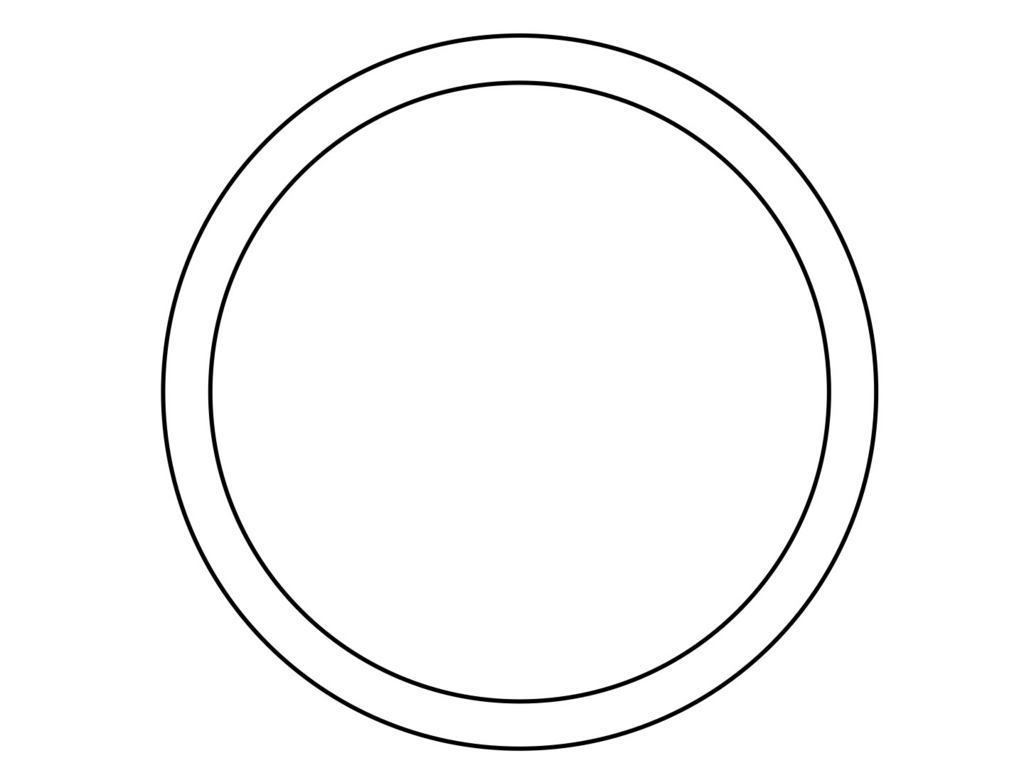
ポアンカレ円板上に8つの円弧が描かれています。半径は,「外側の円」の半径と同じです。
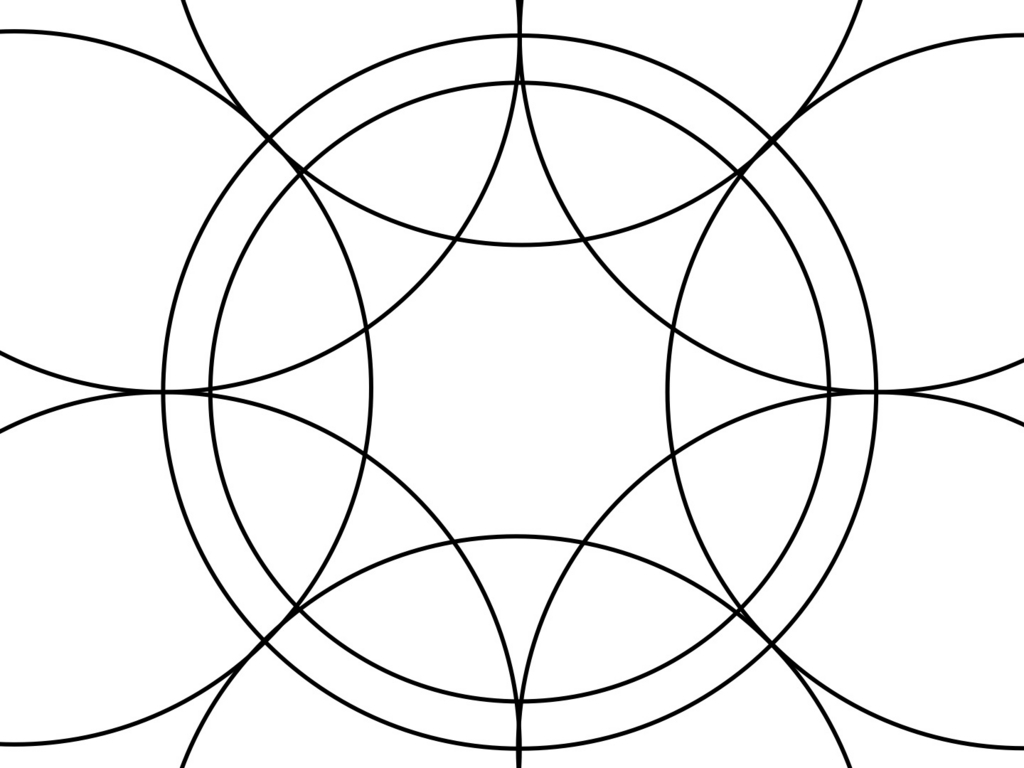
これに色を塗れば完成です。

簡単に解説すると,この8つの円弧はすべて「外側の円(以下の図の黒い太線)」と直交しています。

実物の方はこんな感じです。

「外側の円」と直交する円弧は,双曲平面における「直線(正確には測地線)」となります。したがって,この図形は双曲平面における8つの「直線」に囲まれた図形,すなわち「正八角形」というわけです(対称性より,直線の長さは等距離)。
というわけで,まさに双曲平面を表したようなタイルになっていますね。
せっかくなので,ポアンカレ円板の数学的性質について触れておきましょう。ポアンカレ円板上では,双曲平面は「(2) 縮尺を歪ませて平面に無理やり表されている」ため,「距離の定義」は場所によって異なります。通常,これは次のような「計量」と呼ばれる式によって表されます:
この式の意味するところですが,ユークリッド平面における計量は になりますので,ポアンカレ円板は係数の
だけ「距離の基準」が異なると考えることができます。
は原点からの距離を表すので,原点から離れれば離れるほど,「距離の基準」が長くなるというわけです。
たとえば,図のように点 をとったとします。
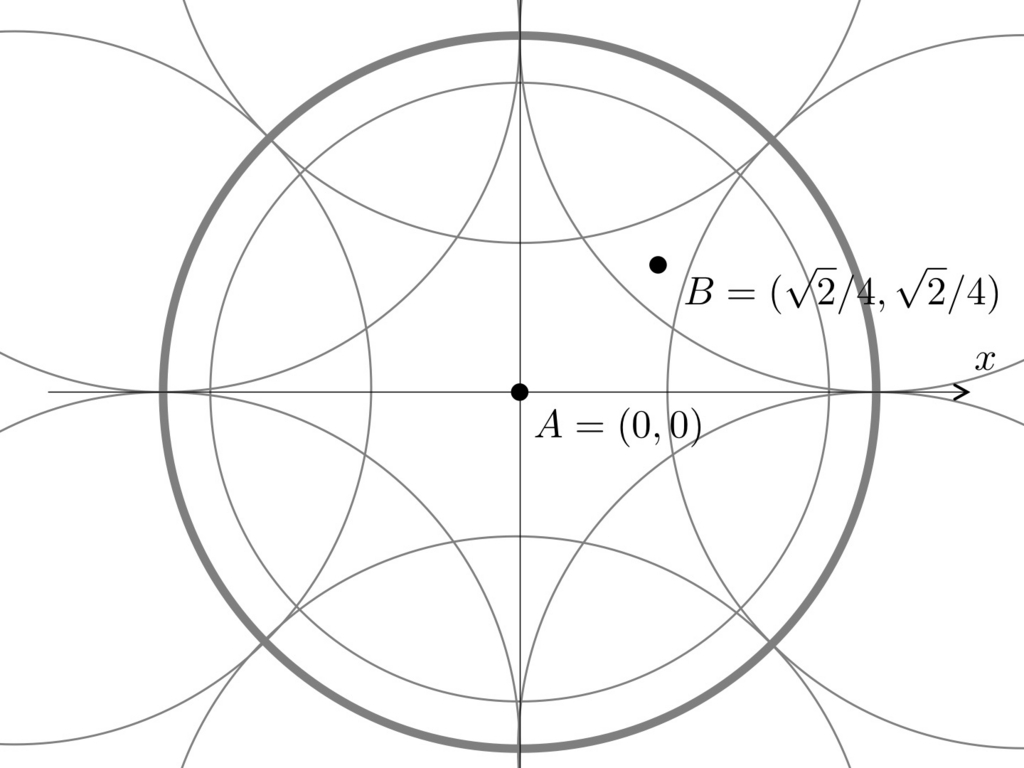
このとき,地点 の計量は
となり,地点 の計量は
となります。つまり, に対して
の方が,
4倍2倍も距離が長くなるということです。
このように,「外側の円」に近づけば近づくほど,双曲平面における距離が長くなっていきます。最終的には,距離は無限に大きくなりますから,いつまでたっても「外側の円」に到達しません。この意味で,「外側の円」は「世界の果て」だというわけです。
さて,このポアンカレ円板のタイルですが,4箇所あります。せっかくなので,その場所を紹介しましょう。私が行ったときには,うっかりしていて場所を正確に記録しなかったのですが,先日名古屋旅行に行った知人に記録してもらうことができました。感謝です。
まず,ポアンカレ円板のタイルが描かれた地下街は,名古屋の栄駅の近くにある「森の地下街」というところです。栄の三越付近の入り口から地下街に入ります。
すると「クリスタル広場」と書かれた場所にでます。そこが「サカエチカ」という地下街です。
森の地下街は,サカエチカと連結しています。森の地下街についたら,以下の地図の該当する箇所(①〜④)に行ってみてください。
対応するタイルはこちらの4つです:




ちなみに、私が見つけたタイルは2つだけだったのですが、知人があと2つ見つけてくれて、全部で4つになりました。たぶんこれですべてだと思います。
その知人の指摘なのですが,2種類のポアンカレ円板の上には黄色い点字ブロックが載っています。この線は世界の端からポアンカレ円板をまたいでいるわけですから,双曲平面上で観測すると無限に長い点字ブロックになっているわけですね。そう考えると面白いかも。
「ポアンカレ円板」といえば,tsujimotterは以前こんなものを作っていました。ポアンカレ円板に触れ合いたい方は,ぜひこちらをどうぞ。
tsujimotter.hatenablog.com
おわりに
名古屋の街で,双曲平面の2つの代表的なモデルである
- ベルトラミーの擬球(3次元空間への埋め込み)
- ポアンカレ円板(2次元平面への埋め込み)
に見えるデザインを見つけることができました。
こんなにもたくさんの双曲幾何学がちりばめられているなんて・・・名古屋はなんて双曲幾何が好きな街なんだ。
というのは冗談として,こうして双曲幾何のことを知っているだけで,これまで気にも留めなかった街の風景を楽しむことができるかもしれないのです。
(実際,tsujimotterはこんだけはしゃいでいた一方で,通りすがりのほとんどの人は図形に目もくれていなかったように思います。)
ここでお伝えしたいメッセージは一つです。
数学を知ると世界を少し広がって、楽しいかも!
それでは今日はこの辺で!
謝辞
教えていただいた @alytile さんに感謝です。(呟いてみるもんだなぁ,と思いました!)
名古屋旅行の最中に時間を割いてポアンカレ円板を探してくれた知人にも感謝。
あと,この数学ツアーに付き合っていただいた,私の先生にも感謝です。
(先生には,実はガロアの弾丸ツアーにも付き合っていただいています。本当にいつもありがとうございます。)
*1:栄駅周辺にある松坂屋の「あつた蓬莱軒」というお店のひつまぶしが大変美味しいです。


