二次体 Q(√-5) のイデアル類群と xx + 5yy 型の二次形式

「イデアル類群は，単項イデアル整域からどれだけ離れているかを測る "ものさし" である」

というような文章は，イデアル類群を簡単に説明するためによく用いられる解説ですが，こんな説明を聞いても「はぁ？何言ってるの？」という感じだと思うのです。

少なくとも私は納得ができませんでした。

イデアル類群には，もっと具体的な意味があるように思うのです。これについて今日は話したいと思います。
（前回に引き続き，本記事の難度は少し高めです。また，以降は「ですます」調から「である」調へと変わります。）

イデアル類群とは

前回話したように，二次体の整数環におけるイデアルは，必ずしも単項イデアルとは限らない。

すべてのイデアルが単項イデアルであるような整数環は「単項イデアル整域（PID）」といって，（数において）素因数分解の一意性が保たれるなど，扱いやすい整数環である。一方，単項イデアル整域でない整数環においては，単項イデアルは可算無限個あるし，そうでないイデアルも可算無限個ある。これだけの情報ではイデアルの全体がどうなっているのかよくわからない。

「単項イデアル」と「単項イデアルでないイデアル」との間の関係を具体的に記述するのが，何を隠そうイデアル類群なのである。

たとえば，二次体 $K = \mathbb{Q}(\sqrt{-5})$ の場合を考えよう。 $K$ の整数環 $\mathcal{O}_K$ を考えて， $\mathcal{O}_K$ のイデアル全体の集合を $\mathcal{J}_K$ ，その部分集合で単項イデアルのみをすべて並べた集合を $\mathcal{P}_K$ としよう。（正確に言うと， $\mathcal{J}_K$ ， $\mathcal{P}_K$ はそれぞれ「分数イデアル」「単項分数イデアル」の集合なのだが。まぁ，細かいことは気にしないでほしい。）

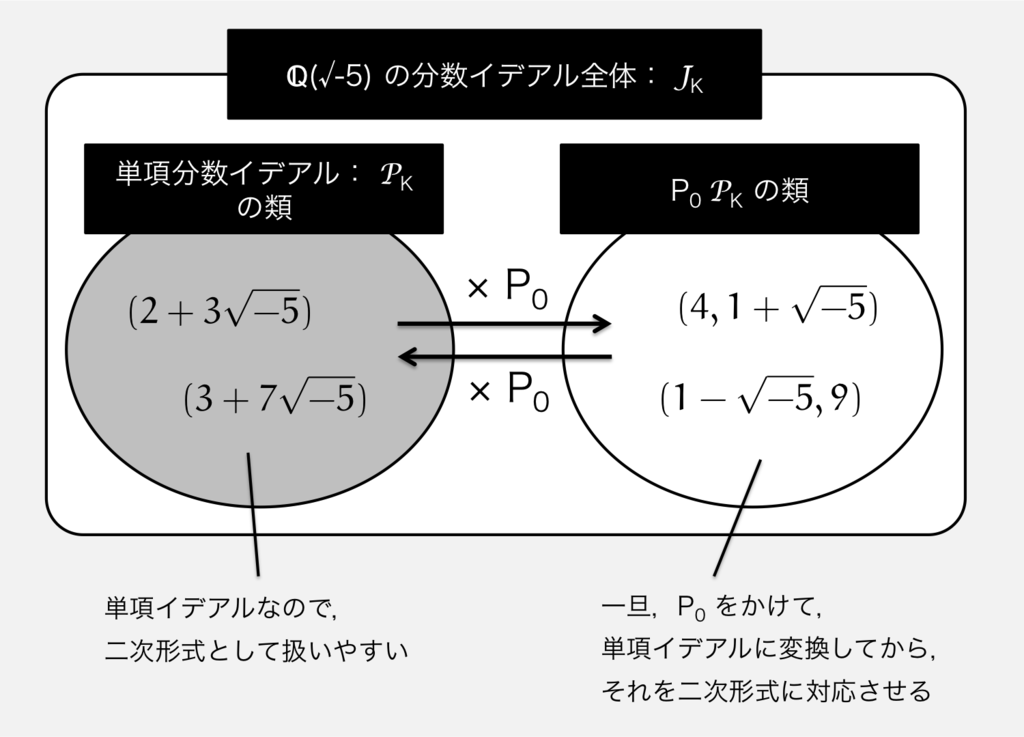
ここで面白いことが起きる。 $K = \mathbb{Q}(\sqrt{-5})$ の場合， $\mathcal{P}_K$ に属さないすべての $\mathcal{J}_K$ の元は， $\mathcal{P}_K$ の元にイデアル $(2, \; 1+\sqrt{-5})$ をかけた形で記述できるというのである。

$P_0 = (2, \; 1+\sqrt{-5})$ とおけば， $\mathcal{J}_K$ のすべての元は， $\mathcal{P}_K$ の類か， $P_0 \mathcal{P}_K$ の類か，どちらか一方に類別されるのだ。

これを数式で記述すると，

$\mathcal{J}_K \big/ \mathcal{P}_K = \{\mathcal{P}_K, \; P_0 \mathcal{P}_K \}$

である。

さらにいうと，各類の間で演算を定義することが出来る。類 $\mathcal{P}_K$ の元に，類 $P_0 \mathcal{P}_K$ の元をかけると，類 $P_0 \mathcal{P}_K$ の元になる。ほかの組み合わせに対する演算も自然に定まる。そして，この演算は群をなすのだ。この群を $K$ のイデアル類群と呼び，以下のように表す。

$\mathcal{C}_K = \mathcal{J}_K \big/ \mathcal{P}_K$

すべての類は $P_0 \mathcal{P}_K$ によって生成され， $P_0 \mathcal{P}_K$ を２回掛けると元の類に戻ってくるから， $\mathcal{C}_K$ は２次の巡回群である。

必ずしもいつもこのような簡単な群で表せるとは限らない。群の構造が複雑になればなるほど「単項イデアルへの戻し方」が複雑になるので「より単項イデアル整域から離れている」とみることも出来るかもしれない。

ところで，なぜわざわざ単項イデアルとの関係で考えるのか。それは，単項イデアルが扱いやすいからだ。

単項イデアルは，１つの代数的整数 $n$ と全単射によって一対一で結ばれる。次のような写像を考えればよい。

$\begin{eqnarray} f\colon & \mathcal{O}_K & \longrightarrow & \mathcal{P}_K \\ & n &\longmapsto & (n) \end{eqnarray}$

こうすると，単項イデアルはもはや数そのものである。

一方で，ほかのイデアルはそうはいかない。まったく扱えないかといえば，そうではなくて，イデアル類群の類の中から逆元を見つけて，それを掛けてあげれば単項イデアルになるのだ。こうすれば数と同一視できて同じように扱うことが出来る。

「二次体 $K$ のイデアル類群の構造が $K$ の扱いやすさを表している」ということが分かって頂けたであろうか。

以降では， $K = \mathbb{Q}(\sqrt{-5})$ のイデアル類群 $\mathcal{C}_K$ の具体的な計算と，その応用として二次形式 $x^2 + 5y^2$ で表すことができる素数について考えていこうと思う。

イデアル類群の計算方法

まず，二次体 $K = \mathbb{Q}(\sqrt{m})$ の判別式は以下で定義される。

$\displaystyle d_K = \begin{cases} m & (m\equiv 1 \pmod 4) \\ 4m & (m\equiv 2,3 \pmod 4) \end{cases}$

次に，集合 $S_K$ を考える。

$\displaystyle S_K = \left\{ p \mid p\leq M_K \;\; かつ \;\; \chi_{d_K}(p) \neq 1 \;\; となる有理素数 \; p \right\}$

$M_K$ は Minkowski の境界といって，定義は以下の通り。

$\displaystyle M_K = \begin{cases} \displaystyle \sqrt{\frac{d_K}{2}} & (d_K > 0) \\ \displaystyle \sqrt{\frac{|d_K|}{3}} & (d_K < 0) \end{cases}$

$\chi_{d_K}(p)$ は以下の式で定義される指標である。

$\displaystyle \chi_{d_K}(p) = \begin{cases} \displaystyle \left(\frac{d_K}{\;p\;} \right) & (p \nmid 2d_K \;\; \unicode[sans-serif]{x306E} とき) \\ \displaystyle \left(\frac{2}{|d_K|}\right) & (p = 2 \;\; かつ \;\; 2 \nmid d_K \;\; \unicode[sans-serif]{x306E} とき) \\ \displaystyle \;\;\;\; 0 & (p \mid d_K \;\; \unicode[sans-serif]{x306E} とき) \end{cases}$

これで，有理素数の集合 $S_K$ が出来たわけだか，これを次のように使うのである。

《定理》
イデアル類群 $\mathcal{C}_K$ は， $S_K$ に属する有理素数を割る素イデアルの類により生成される。
特に， $S_K = \emptyset$ ならば $\mathcal{C}_K = \{\mathcal{P}_K\}$ である。

これにて，イデアル類群 $\mathcal{C}_K$ を作ることが出来る。ついでに， $M_K$ は有限より， $\mathcal{C}_K$ が有限群であることも分かった。

いろいろ条件分岐が多くてややこしくみえるかもしれないが，実際計算してみるとそれほど難しいわけではない。次の項でやってみよう。

K = ℚ(√-5) のイデアル類群

二次体 $K = \mathbb{Q}(\sqrt{-5})$ を考える。

$m = -5\equiv 3 \pmod 4$ より，判別式は，

$d_K = 4\cdot (-5) = -20$

である。

次に， $M_K$ は，

$\displaystyle M_K = \sqrt{\frac{|d_K|}{3}} = \sqrt{\frac{20}{3}} = \sqrt{6.66...} \approx 2.58$

であるから， $S_K$ の上限は $2$ である。

ここで， $2 = p \mid d_K = -20$ より，

$\chi_{-20}(2) = 0 \neq 1$

である。したがって， $2$ は $S_K$ の要素である。

以上から， $S_K = \{2\}$ が分かったので，これを割るような素イデアルを探せばよい。今回のケースでは，これはあっさり見つけることが出来て，

$(2, \; 1+\sqrt{-5}) (2, \; 1-\sqrt{-5}) = (2)$

より， $P_0 = (2, \; 1+\sqrt{-5})$ は $(2)$ を割り切る。したがって， $P_0 = (2, \; 1+\sqrt{-5})$ はイデアル類群 $\mathcal{C}_K$ の類の代表元である。

$P_0$ が単項イデアルでないことは，前回示したから， $P_0 \not\in \mathcal{P}_K$ である。

したがって， $K$ のイデアル類群 $\mathcal{C}_K$ は以下のように求まった。

$\mathcal{C}_K = \{\mathcal{P}_K, \; P_0 \mathcal{P}_K \}$

めでたしめでたしである。

(p) を割る素イデアル

ところでふと，この辺の計算は機械的にプログラムに出来そうだなと思ったのだ。しかし，少し考えてみると $(p)$ を割る素イデアルを見つけるフェーズが難しそうである。

そう思っていたら，意外と簡単な方法が見つかった。

《(p) を割る素イデアル》
素数 $p$ に対し， $\mathcal{O}_K = \mathbb{Z}[\sqrt{-5}]$ の素イデアル $P = (p, \; x+y\sqrt{-5})$ を考えると， $P$ は $(p)$ を割り切る。
$(p, \; x+y\sqrt{-5}) \mid (p)$

ただし， $x, y$ は以下を満たす整数。
$p \mid x^2+5y^2$

証明は結構簡単。

$(p, \; x+y\sqrt{-5}) (p, \; x+y\sqrt{-5})' \\ = (p^2, \; p (x+y\sqrt{-5}), \; p( x-y\sqrt{-5}), \; x^2 + 5y^2 )$

$p \mid x^2+5y^2$ より， $kp = x^2+5y^2$ とおくと，

$= (p^2, \; p (x+y\sqrt{-5}), \; p( x-y\sqrt{-5}), kp ) \\ = (p)(p, \; x+y\sqrt{-5}, \; x-y\sqrt{-5}, \; k)$

ここで， $x - y\sqrt{-5} = 2x - (x + y\sqrt{-5})$ より，

$= (p)(p, \; x+y\sqrt{-5}, \; 2x, \; k)$

さらに， $(p, \; 2x) = (1)$ より，

$= (p)(1) = (p)$

よって， $(p, \; x+y\sqrt{-5})$ は $(p)$ を割り切る。

また， $P$ のノルムが有理素数であることから， $P$ は素イデアル。

■

この方法は次の項でも用いる。

二次形式への応用

$K = \mathbb{Q}(\sqrt{-5})$ のイデアル類群の応用として，ラグランジュが証明した二次形式の定理について考えようと思う。

フェルマーは $p \equiv 1 \pmod 4$ となる素数 $p$ は，

$p = x^2+y^2$

の形でかけることを示した。その後，誰によってか知らないが $p \equiv 1, 3 \pmod {8}$ となる素数 $p$ が

$p = x^2+2y^2$

の形で表せることが，オイラーによって $p \equiv 1, 3, 7 \pmod {12}$ となる素数 $p$ が

$p = x^2+3y^2$

の形でかけることが，それぞれ示されている。

どのケースも， $\mod {4n}$ の条件によって，二次形式 $x^2 + ny^2$ でかける素数の種類が決まることになる。したがって， $\mod {20}$ の条件によって $x^2 + 5y^2$ でかける素数の種類が決まるのでは，と考えるのはきわめて自然な流れだろう。

しかしながら，そうは問屋が下ろさない，というのが次の定理である。

《定理： $x^2+5y^2$ 型の二次形式》
素数 $p$ に対し，それぞれ以下が成り立つ。

(a) $p\equiv 1, 9 \pmod {20}$ のとき：
$p = x^2 + 5y^2$ を満たすような整数 $x, y$ が存在する．
(b) $p \equiv 3, 7 \pmod {20}$ のとき：
$2p = x^2 + 5y^2$ を満たすような整数 $x, y$ が存在する．

$p \equiv 1, 3, 7, 9 \pmod{20}$ のときには，素数 $p$ は二次形式（のようなもの）に表せるのであるが，その形は２パターンに分かれるというのが上の定理の主張である。

実は「この２パターンに分かれる」というのが，イデアル類群の位数 $\left| \mathcal{C}_K \right|$ が $2$ であることに深く関係する。

もう少し正確に言うとこうだ。１つのイデアルに１つの二次形式が対応する。もしそのイデアルが $\mathcal{C}_K$ の類のうち $\mathcal{P}_K$ に属していれば，ケース (a) の形の二次形式となる。もし $P_0 \mathcal{P}_K$ に属していれば，ケース (b) の二次形式が出来上がるという寸法だ。使用するイデアルがどちらの類に所属しているかどうかで，出来上がる二次形式の形が変わるのだ。

f:id:tsujimotter:20150812201241p:plain:w600

では，証明に移ろう。

まず，以下の《補題》から示そう。

《補題》
$p \equiv 1, 3, 7, 9$ ならば， $p \mid x^2 + 5y^2$ を満たす， $x, y \in \mathbb{Z}$ が存在する

平方剰余 $\displaystyle \left(\frac{-5}{\;p\;}\right)$ を考える。

定義より， $\displaystyle \left(\frac{-5}{\;p\;}\right) = 1$ であれば，

$x^2 \equiv -5 \pmod {p}$

となるような， $x \in \mathbb{Z}$ が存在する。移項して変形すると，

$x^2 + 5\cdot 1^2 \equiv 0 \pmod {p}$

となり $y = 1$ とすると， $p \mid x^2 + 5y^2$ を満たす， $x, y \in \mathbb{Z}$ が存在すること示せた。

あとは， $\displaystyle \left(\frac{-5}{\;p\;}\right) = 1$ となる $p$ の条件であるが，

$\displaystyle \left(\frac{-5}{\;p\;}\right) = \left(\frac{-1}{\;p\;}\right) \left(\frac{5}{\;p\;}\right)$

平方剰余の相互法則より，

$\displaystyle \left(\frac{-1}{\;p\;}\right) = 1 \Longleftrightarrow p \equiv 1 \pmod 4, \hspace{32px} \left(\frac{-1}{\;p\;}\right) = -1 \Longleftrightarrow p \equiv 3 \pmod 4$

$\displaystyle \left(\frac{5}{\;p\;}\right) = 1 \Longleftrightarrow p \equiv 1, 4 \pmod 5, \hspace{32px} \left(\frac{5}{\;p\;}\right) = -1 \Longleftrightarrow p \equiv 2, 3 \pmod 5$