空の見えないセカイ - tsujimotterのノートブック

この記事は Math Advent Calendar 2015 の 23日目の記事です。（22日目：実数の実体）

昨日の記事は、さわらさん（@sawara0804）による「実数の実体」というお話でした。私の琴線にヒットしそうなお話で大変興味があるのですが、すみませんまだ読めていません。年末にゆっくり読ませていただきたいと思います。

さて、Math Advent Calendar の予定欄には

「NHKの数学ミステリー白熱教室で話していた内容に関連する話を書きたいです」

と書いておりましたが、予定を変更したいと思います。白熱教室の話を期待された方には申しわけありません。また機会を見つけて書きたいと思っています！
（数学ミステリー白熱教室、超おもしろかったですね！）

今回のタイトルが「空の見えないセカイ」という、ラノベっぽい（煽り気味の）タイトルでびっくりされたかもしれませんが、ちゃんと数学のお話です。笑

昨日、twitterのフォロワーさんとお話していて、ふと思いついた問題です。思いついて、どうしても書きたくなってしまったのでこちらにテーマ変更させていただきました。

それでは、こんな思考実験を考えてみましょう。

＊　＊　＊　＊　＊

二次元人がいます。
図のように壁がそびえ立っていて、その崖のふもとに立って、空を見上げているとします。

f:id:tsujimotter:20151223165241p:plain:w400

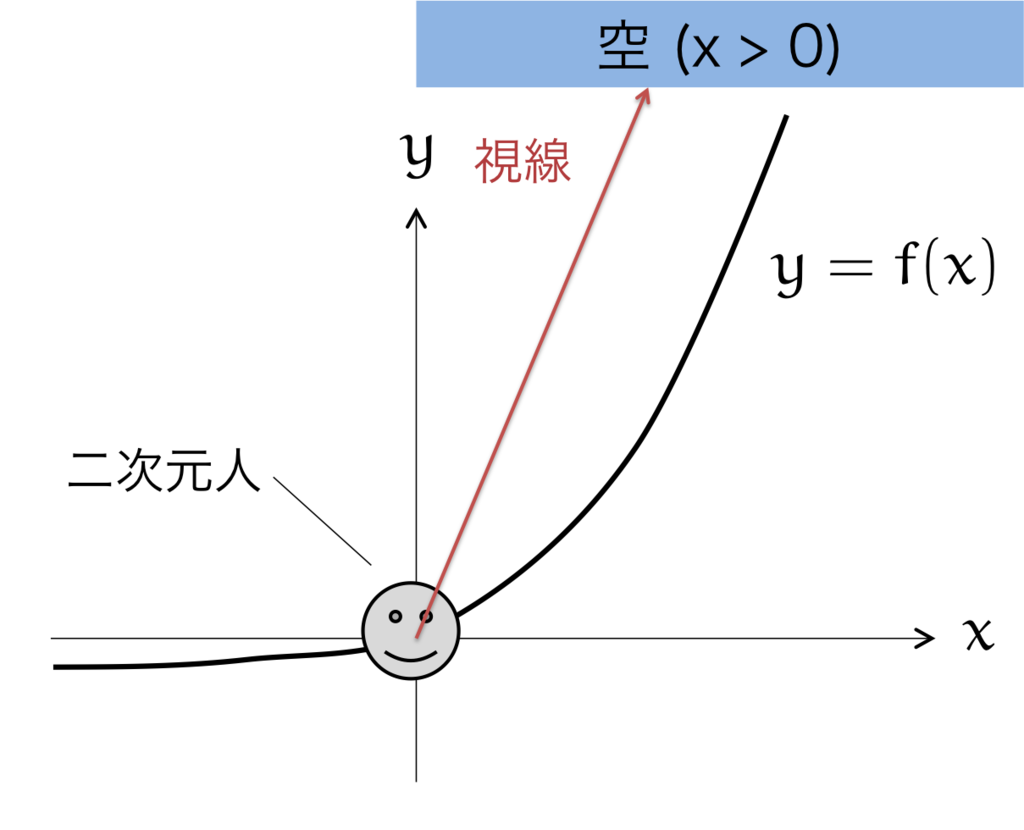
崖の形状は $y = f(x)$ のグラフによって定まります。

$f(x) = e^x-1$ （指数関数）であるときに、二次元人は $x > 0$ にある空のうち、どの領域を見ることができるだろうか。

ちなみに、 $e^x - 1$ のように $-1$ している理由は、崖を原点に合わせるためです。二次元人の視点は、原点からはじまっているとします。

＊　＊　＊　＊　＊

指数関数なので急激に崖はおおきくなってしまいますが、直感的にはある程度の領域の空は見えそうな気がしますね。

ところが、答えはとても意外なものになります。

自分で考えてみたい方は、ここで止めて考えてみてください。

↓　↓　答えはこちら　↓　↓

答え：
$x > 0$ の空は見えない。

いったいどういうことでしょうか。

先ほどの図をもう少しスケールを上げて考えてみましょう。

f:id:tsujimotter:20151223170011p:plain:w400

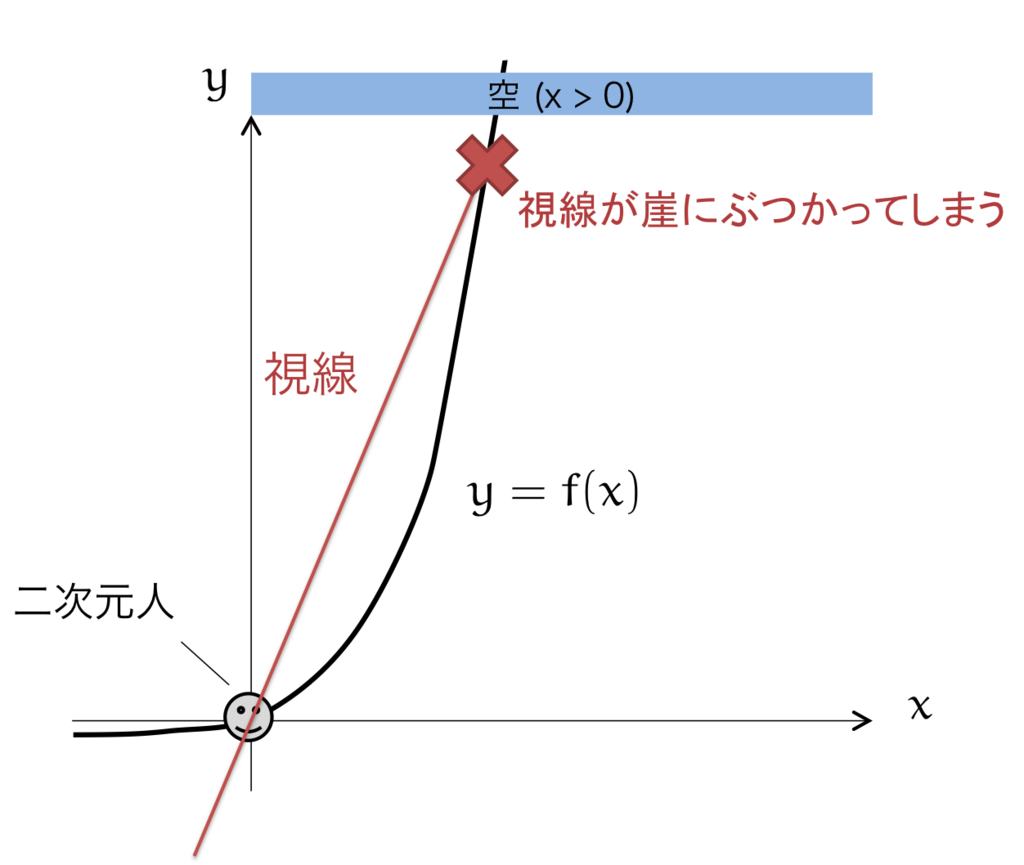
視線は一直線上に進むわけですから、

$y = Cx$

のように置くことができます。 $C$ は定数です。

上の図の場合は、視線が崖にぶつかってしまいました。視線が崖にぶつかると、その先の空は見えません。空を見るためには、もう少し視線を上げる、すなわち、 $C$ を大きくする必要があります。

結局のところ「空がみえる」というのは、視線が崖の上を常に超える、ということです。すなわち、数学的には「 $f(x) < Cx$ を満たす係数 $C$ が存在する」ということです。

$f(x) = e^x - 1$ より、条件は

$e^x - 1 < Cx \hspace{20px} (\forall x > 0)$

です。

少し考えると分かりますが、このような条件を満たす係数 $C$ は存在しません。したがって、 $x > 0$ の空が見えない、というのが回答になるわけです。

「空が見えるか？」という問題が「 $f(x) < Cx$ を満たす係数 $C$ が存在するか？」という数学の問題に置き換わる、というのが非常に面白いなと思いました。

もう少し発展させられる

この問題はもう少し進めることができます。指数関数は少し条件としてきつすぎるからです。

実際、 $f(x) = x^2$ としても、

$x^2 < Cx \hspace{20px} (\forall x > 0)$

をみたす $C$ は存在しません。

もっと言えば、指数が $1$ より少しでも大きくできればよいわけですから、

$x^{1+\epsilon} < Cx \hspace{20px} (\forall x > 0)$

として、 $\epsilon$ は $\epsilon > 0$ を満たす実数としておけばよいでしょう。 $\epsilon$ はいくら小さくとったとしても、 $x^{1+\epsilon} < Cx$ となるような、 $C$ は存在しません。

きっかけ

この話のきっかけは、twitterで数学を面白おかしく伝える活動をされている「鯵坂もっちょさん」という方の以下のツイートでした。

あのニコファーレでやった3Dのゼータの中に入ってみるやつ、青空が広がってたからのどかな雰囲気だったけど実際は視界のほとんどが天までそそり立つ壁なわけで相当威圧感あるよね
— 鯵坂もっちょ (@motcho_tw) December 21, 2015

私がニコニコ学会というイベントでゼータ関数の景色を3Dで見せるデモンストレーションを行ったのですが、上はそれを受けてのツイートです。
左半平面においてはゼータ関数は指数的に増加するはずなので、先の議論により空がみえないはずだ、と答えたのでした。

興味深い問題のきっかけを与えてくださってありがとうございました。^_^

f:id:tsujimotter:20151224013307p:plain:w400

図：ゼータ関数と話題の崖の部分（参考画像）

おわりに

今回の話は、結果的には

$f(x) < Mg(x)$

となる定数 $M$ が存在するか、という数学的には「オーダー」の話だったわけですね。

一方で、いきなりこのような記号を見せられても、ちょっととっつきにくいかもしれません。そんな抽象的な話でも「空が見せるかどうか」という非常に直感的な問題に落とせるかもしれない、というのが今回のポイントだったように思います。

抽象的な数学が得意でない人にも、興味をもってもらえるきっかけを与えられるかもしれない、という可能性にウキウキした tsujimotter でした。

まだ、この問題は１日しか考えていない問題なので、仮定を加えたりさらに一般化したりとまだまだ遊べるかもしれません。ぜひチャレンジしてみてください。^_^

それでは今日はこの辺で。

明日は、taketo1024さんの『「プログラマのための数学勉強会」を振り返って』というお話です。プログラマの数学勉強会は、今年から始まったイベントですが、tsujimotterも大変お世話になりました。数学の講演活動を始めたのもこの会がきっかけですし、数学を一緒に語り合える仲間ができたのもこの会のおかげです。思えば、taketo1024さんとはじめて出会ったのも、昨年のアドベントカレンダーがきっかけでした。明日は素敵な記事を楽しみにしています！