接吻数問題と 24 次元リーチ格子

「接吻数問題」という数学の問題があります．なんとも変な名前の問題ですが今日はそのお話です．

実は今回のテーマは，私が１年半前に書いた 691 の記事に深く関連しています．私のブログでしばしば取り上げている「ラマヌジャンのデルタ」や「保型形式」といったトピックにも深く関連しています．

上記をブログで書いた当初は，今回のテーマ（特に「リーチ格子」について）はまったく理解していませんでした．調べても調べても私が理解できる解説に行き当たらず，諦めて断念してしまっていたのです．

ところがついさっき，ふと調べ直してみたところ，当時どうしても理解できなかった概念が，なんともすっきり理解できてしまいました．これまでの蓄積した知識が数珠つなぎ的につながったような不思議な感覚でした．

「これはブログにまとめるしかない！」と思い立って，興奮を抑えつつ（あまり抑えきれていませんが）この記事を書いています．

小難しい話も入ってきますが，とてもわくわくするトピックだと思いますので，ぜひご覧ください！

接吻数問題

接吻数 とは「 $n$ 次元の空間に半径 $1$ の単位球を重ならず触れ合うように置いたとき，１つの球の周りに置くことができる球の最大数」のことです．この接吻数を求める問題のことを「接吻数問題」といいます．

接吻数という風変わりな名前がついている由来は，たとえば２次元のケースを思い浮かべればわかります．

https://upload.wikimedia.org/wikipedia/commons/d/d2/Kissing-2d.svg

真ん中の円の周りを，周りの６個の円が「まるで中心の円にキスをするように」接していますね（英語だと，接吻数のことを "kissing number" といいます）．２次元の場合，これ以上多くの円を「キスさせる」ことができません．したがって，２次元の接吻数は $6$ となります．

同様に３次元を考えると，以下のように $12$ 個の球が接することがわかります．

f:id:tsujimotter:20160807211808p:plain:w200

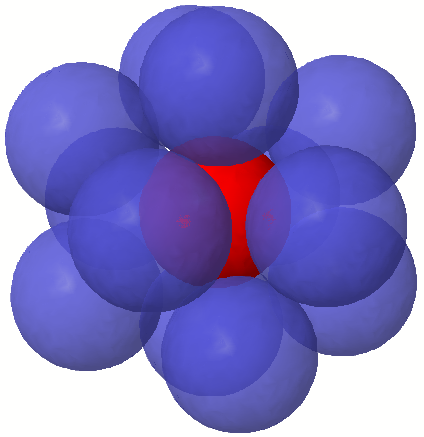
証明は簡単ではありませんが，これ以上多くの球が接することはできません．したがって，３次元の接吻数は $12$ です．

一般に，次元が高くなればなるほど，接することのできる方向が増えるので，接吻数も増えていきます．

次元 $n$ に対する接吻数問題は， $n = 2, 3$ のほか， $n$ が特別な場合に限り解決しています．Wikipedia によると，2016 年現在，すでに確定している接吻数は，以下の表にあるものがすべてです．

次元数 $n$	接吻数
$1$	$2$
$2$	$6$
$3$	$12$
$4$	$24$
$8$	$240$
$24$	$196560$

ほかの次元においては，接吻数のとりうる上限と下限がわかっている次元もありますが，１つの値に確定してはいません．つまり，接吻数はまだ求まっていません．求まるかどうかもわかりません．

ここで気になるのは，

なぜ $24$ 次元は求まるのか

ってことですよね！

このような $24$ 次元の特異性には「リーチ格子」と呼ばれる数学的な対象が深く関わっています．リーチ格子を理解するために，まずは基本的な「格子」という考え方についてお話ししましょう．

格子（Lattice）とは

格子とは， $n$ 次元ユークリッド空間 $\mathbb{R}^{n}$ の離散部分群で， $n$ 個の基底ベクトルによって生成される空間のことです．

生成する $n$ 次元基底ベクトルの集合を $\{ v_1, v_2, v_3, \cdots, v_n \}$ とすると，格子 $\Lambda$ は

$\Lambda := \left\{ k_1 v_1 + k_2 v_2 + k_3 v_3 + \cdots + k_{n} v_{n} \;\; \middle| \;\; k_1, k_2, k_3, \cdots, k_{n} \in \mathbb{Z} \right\}$

によって定義されます．格子の元を 格子点 と呼びます．

定義は一見難しそうですが，具体的に考えればそれほど難しくありません．

たとえば， $n = 2$ 次元として，以下の２つの基底ベクトルを考えましょう．

$v_1 = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \; \; v_2 = \begin{pmatrix} 0 \\ 2 \end{pmatrix}$

これら２つの基底で生成される格子点の座標を $(x, y)$ で表したとき， $x, y$ がともに偶数となります．図に表すとこんな感じです．

https://upload.wikimedia.org/wikipedia/commons/thumb/6/63/SquareLattice.svg/200px-SquareLattice.svg.png

図における点１つ１つが格子点で，すべての格子点の集合が格子です．隣り合う格子点の最小の距離は $2$ となります．

もう１つ例をあげましょう．２つの基底ベクトルを以下のように考えます．

$v_1 = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \; \; v_2 = \begin{pmatrix} 1 \\ \sqrt{3} \end{pmatrix}$

これら２つの基底は，ベクトルのなす角が $60$ 度となっています．したがって，生成される格子点は，以下のように「正三角形」を並べたようになります．

この場合も，隣り合う格子点の最小の距離は $2$ となります．

以上の格子は，それぞれ「隣り合う格子点の最小の距離」が $2$ であるように選んだ格子です．これらの格子を接吻数問題に応用してみましょう．

まず図中に，それぞれの格子点を中心とした半径１の球（この場合，２次元なので「円」となります）を置きます．すると「隣り合う格子点の最小の距離は $2$ 」より，隣り合う円は接することになります．また，最小性より円は互いに重なり合うことはありません．

最初の格子では，１つの円に接する円の数は４つです．２つ目の格子においては，１つの円に接する円の数は６つです．したがって，２つの格子を比べると，２つ目の方が接吻数問題においては「より良い格子」と言うことができそうです．

接する球の数がもっとも大きな格子，すなわち，最密な格子を見つけることができれば，接吻数問題は解決です．実際，２次元においては，２つ目の格子が最密な格子となります．

ここまでが「格子を用いた接吻数問題へのアプローチ」の基本的な考え方です．

ところで，上の例では２次元を扱っていたので図を用いて表すことができますが，（３次元はともかく）４次元以上になると図なんか書いていられないですね．より抽象的な議論が必要になります．

一般に格子は，格子を生成する列ベクトルを横に並べた行列によって表現されます．

最初の格子は，

$A = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}$

という行列で表され，２番目に例に挙げた格子は，

$A = \begin{pmatrix} 2 & 1 \\ 0 & \sqrt{3} \end{pmatrix}$

という行列によって表される格子です．

以下では，行列や線形代数の技術を使って，数学的な議論を展開していきます．

次元が高くなれば，格子は目で見えなくなりますが，数式を通して心の目で覗いてみてください．

それでは，本題の２４次元の格子を考えていきましょう．

24次元リーチ格子

$24$ 次元リーチ格子は， $24$ 次元ユークリッド空間 $\mathbb{R}^{24}$ の部分集合で，以下の行列によって生成される空間です．

$A := \frac{1}{\sqrt{8}}\begin{pmatrix} 8 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & 2 & 2 & 0 & 0 & 0 & 0 & 2 & 2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 2 & 0 & 2 & 0 & 0 & 2 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 2 & 2 & 2 & 0 & 0 & 2 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 2 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & 0 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 2 & 0 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 2 & 2 & 2 & 2 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 \\ −3 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{pmatrix}$

この行列の各列を

$A = (v_1, \; v_2, \; v_3, \; v_4, \; \cdots, \; v_{23}, \; v_{24})$

という $24$ 個の独立な基底ベクトルで表現したとき，リーチ格子 $\Lambda_{24}$ は以下のように定義されます．

$\Lambda_{24} := \left\{ k_1 v_1 + k_2 v_2 + k_3 v_3 + \cdots + k_{24} v_{24} \;\; \middle| \;\; k_1, k_2, k_3, \cdots, k_{24} \in \mathbb{Z} \right\}$

基底が一気に $24$ となっていますが，２次元のときと考え方は同じです．

問題はリーチ格子の最密性ですが，結論から言うと $24$ 次元においてはリーチ格子が最密であることが示されています．すなわち， $24$ 次元においては，リーチ格子よりも密度の高い球充填はできません．

最密性さえ示せれば，リーチ格子を調べることで $24$ 次元の接吻数が定まりますので，接吻数問題において最密性の証明は非常に重要です．一方で，残念ながら私のブログで書くには荷が重すぎるかもしれません．
（どうやって示すのだろう．ちょっとわかりません．*1）

そこで今回は，最密性を示す代わりに，

「接吻数 $196560$ がいかにして求まるか」

という問いに焦点を絞りたいと思います．これも非常に面白いんですよ，奥さん．

まず，リーチ格子における３つの重要な性質を確認していきましょう．

1. It is unimodular; i.e., it can be generated by the columns of a certain 24×24 matrix with determinant 1.
2. It is even; i.e., the square of the length of any vector in Λ24 is an even integer.
3. The length of any non-zero vector in Λ24 is at least 2.

順番に 1. の「行列式は $1$ 」という性質を確かめてみましょう．

$A = \frac{1}{\sqrt{8}}\tilde{A}$

とおいて，整数行列 $\tilde{A}$ の行列式を計算します．とはいえ，さすがに $24$ 次元行列の行列式を手計算するのはいやですよね．

手元に NumPy の入った Python があったので，それを使うことにします．
gist.github.com

実行結果は次のようになります．

$ python leech.py
68719476736.0

したがって，

$\text{det }\tilde{A} = 68719476736$

が得られました．

$68719476736 = 2^{36}$

より， $A$ の行列式は

$\text{det }A = \text{det}\left(\frac{1}{\sqrt{8}}\tilde{A}\right) = \left(\frac{1}{\sqrt{8}}\right)^{24} \cdot 2^{36} = 1$

となり，たしかに「行列式は $1$ 」が確認できました．

2. 3. の性質の議論はやや難解ですが，接吻数問題においては本質的です．

まず対称性により，原点を中心に考えて良いことがわかります．全体の格子点に「特定の格子点を原点に向けて並行移動させるような変換」を適用してできた集合は，元の格子に一致します．したがって，原点で成り立つことは，任意の点においても同様に成り立つというわけです．

原点からの距離は格子点の「ノルム」に相当するため，「格子点間の距離」を「ノルム」と置き換えて，2. 3. を以下のように言い換えることができます．

2. すべての格子点のノルムの２乗は偶数である．
3. （ $0$ でない）すべての格子点における最小のノルムは $2$ である．

3. の「最小のノルムは $2$ 」ということは，原点にもっとも近い格子点における原点からの距離が $2$ ということです．つまり，各格子点に半径 $1$ の単位球の中心をおけば，すべての球は重なり合うことはなく，かつ最も原点に最も近い球は原点の球と互いに接することがわかります．したがって，この最も原点に近い球の数を数えれば，接吻数が求まります．

あとは，3. を示せばよいですね．この問題を考えるために，以下ではテータ関数と呼ばれる保型形式を導入しましょう．

「え，保型形式！？」と思うかもしれませんが，これが話の肝なんです．

ちなみに「2. すべての格子点のノルムの２乗は偶数である」は，以下の議論のついでに明らかになります．

テータ関数を通してリーチ格子を「ききとる」

上に述べたように，リーチ格子の性質は 保型形式 を通して理解することができます．

一般に格子 $\Lambda$ が与えられると， $\Lambda$ に紐づいたテータ関数 $\Theta_{\Lambda}(\tau)$ を考えることができます． $\Theta_{\Lambda}(\tau)$ は $\text{Im }\tau > 0$ の上半平面で定義される正則関数で，

$\displaystyle \Theta_{\Lambda}(\tau) = \sum_{x\in \Lambda} e^{i\pi \tau \|x\|^2}$

という式で定義されます．

テータ関数の定義をみて「なんだこりゃ」と思うかもしれませんが，具体的に考えればそれほど難しくないとありません．たとえば，格子が $\Lambda = \mathbb{Z}$ のときは，単にヤコビのテータ関数 $\theta(z, \tau)$ において $z = 0$ としたものになります．

$\displaystyle \Theta_{\Lambda}(\tau) = \theta(0, \tau)$

ちゃんと，よく知られたテータ関数になっていますね！

さらに，格子 $\Lambda$ がランク $n$ の行列により生成され 「ユニモジュラー（行列式が１）」かつ「すべての格子点のノルムの２乗が偶数」であるとき，

$\displaystyle \Theta_{\Lambda}\left(\frac{a\tau + b}{c\tau + d}\right) = (cz+d)^{n/2} \Theta_{\Lambda}(\tau), \;\;\;\; \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \text{SL}(2, \mathbb{Z})$

という等式を満たすことが知られています．肩の上に載っている $n/2$ を重さと呼び，このような式を満たす正則関数をを重さ $n/2$ の 保型形式 といいます．

以下では， $\Lambda_{24}$ を $24$ 次元リーチ格子として，そのテータ関数 $\Theta_{\Lambda_{24}}(\tau)$ を考えましょう．リーチ格子 $\Lambda_{24}$ は，ランク $24$ の行列で生成される「ユニモジュラー」かつ「すべての格子点のノルムの２乗が偶数」の格子であるから， $\Theta_{\Lambda_{24}}(\tau)$ は重さ $12$ の保型形式となります．

2016/08/08 訂正：テータ関数が保型形式となる条件が抜けていましたので，補足します．*2

さて，保型形式が出てきたら， $q$ -展開したくなるのが人情というものです．上の式を

$q = e^{2i\pi \tau}$

で置き換えて， $q$ の昇べきの順にまとめたものを，保型形式の $q$ -展開と呼びます． $q$ -展開の係数には，数論的に重要な情報が登場することが多いのです．今回も例外ではありません．

Wikipedia によると，上記のテータ関数は

$\displaystyle \Theta_{\Lambda_{24}}(\tau) = 1 + 196560q^2 + 16773120q^3 + 398034000q^4 + \cdots$

のように展開できるようです．係数を観察すると，なんと $q^2$ の係数に $196560$ が現れます！ゾクゾクしてきませんか！

2016/08/08 訂正：Wikipedia の q-展開の指数が間違っていたので修正しました．*3

実際 $q^{m}$ の係数は，テータ関数の定義より「格子のノルム $\|x\|$ の２乗が $2m$ である格子点の個数」に相当します．

半径 $1$ の球を原点においてみるとその意味がわかります．

最初の $1$ （すなわち， $q^0$ の係数）は，原点からの距離が $0$ である位置に中心がある球の個数です．
次の $196560$ （すなわち， $q^2$ の係数）は，原点からの距離が $2$ である位置に中心がある球の個数です．
その次の $16773120$ （すなわち， $q^3$ の係数）は，原点からの距離が $\sqrt{6}$ である位置に中心がある球の個数です．

なるほど，保型形式の $q$ -展開の係数は「中心の球からの距離が等距離である球の個数を，原点から近い順に並べたもの」だったのですね！

つまり，中心の球に接する球の個数は $q^2$ の係数，すなわち $196560$ であることは明らかです！

面白い！！！

コンウェイ*4 という数学者の著書

素数が香り、形がきこえる-目でみる2次形式 (シュプリンガー数学リーディングス)

作者: J.H.コンウェイ,細川尋史
出版社/メーカー: 丸善出版
発売日: 2012/07/17
メディア: 単行本
この商品を含むブログを見る

では，テータ関数の持つ不思議な性質を，以下のように風に紹介していました．

格子に関するある性質がテータ関数によって決まるとき，その性質はききとれるという．

「ききとれる」という表現いいですよね．格子のテータ関数を通して，格子のことを深く知ることができるのです．今回は，リーチ格子から接吻数を「ききとる」ことができました．

この本自体はなかなかレベルの高い本ですが「二次形式を目で見る」をテーマとしていて，チャレンジングで面白い切り口の本です．

テータ関数の q 係数を具体的に計算する

さて，上のテータ関数における $q$ -展開の係数は，割と容易に求めることができます．計算してみたいですよね！

Wikipedia によると

$\displaystyle \sum_{x\in \Lambda_{24}} q^{\|x\|^2} = \sum_{m=0}^{\infty} \frac{65520}{691}(\sigma_{11}(m) - \tau(m))q^{m}$

が成り立つ，とあります．

ここで， $\sigma_{11}(m)$ は約数の $11$ 乗和関数で， $\tau(m)$ はラマヌジャンの $\tau$ 関数です．

私のブログの読者の中には，上式の係数 $\frac{65520}{691}$ に見覚えのある人もいるかもしれません！

tsujimotter.hatenablog.com

上の記事では，

$65520\cdot \sigma_{11}(n)\equiv 65520\cdot \tau(n) \pmod{691}$

という式が登場していました．これがなんと今回の話につながります． $n\to m$ として変形すると，

$65520(\sigma_{11}(m) - \tau(m)) = 691\cdot k(m)$

となります（ $k(m)$ は $m$ に対して定まる定数）．両辺 $691$ で割ると

$\displaystyle \therefore \frac{65520}{691}(\sigma_{11}(m) - \tau(m)) = k(m)$

となって，たしかに保型形式 $q^{m}$ の係数に一致していますね．

上の記事では $\mod{691}$ をとっていたために， $k(m)$ に相当する部分は考慮しなかったのですが，まさかこのような重要な情報が隠されていたとは．

さて，以上の計算は簡単に実行できますので，具体的に計算してみましょう．ぜひ電卓を持ってきて，一緒にやってみてください！

今回必要なのは $q^2$ の係数，すなわち $m = 2$ のケースだけです．

$m = 2$ における「約数の $11$ 乗和関数」と「ラマヌジャンの $\tau$ 関数」を計算します．この２つの値は，定義より容易に計算できて

$\sigma_{11}(2) = 1^{11} + 2^{11} = 1 + 2048 = 2049$
$\tau(2) = -24$

となります．よって

$\displaystyle \frac{65520}{691}\left(2049 - (-24)\right) = 196560$

が得られます．右辺の数こそ，まさに $24$ 次元の接吻数ですね！！！

なお，以上の計算を私は iPhone の電卓で行ったのですが，テンションが上がりすぎて思わずスクリーンショットを撮ってしまいました．笑

f:id:tsujimotter:20160807231859j:plain:w160

最後に，冒頭の「なぜ $24$ 次元は求まるのか」という問いを回収したいと思います．計算してみて，なんとなくわかってきたのではないでしょうか．

というのも， $24$ 次元のリーチ格子の計算においては， $24$ を $2$ で割った「重さ $12$ の保型形式」の性質をうまーく使っています．たまたま，都合の良い重さ $12$ の保型形式がうまいことあったからこそ実現したわけですね．

そして， $691$ の記事でも書いたように，この重さ $12$ の保型形式は「ラマヌジャンのデルタ」という，極めて興味深い保型形式となっています．「ラマヌジャンのデルタ」がなかったら， $24$ 次元の接吻数問題は解決していなかったかもしれないのです．

おわりに

今日扱ったテーマは幾何学における「接吻数問題」とその解決方法でした．振り返ってみると，その過程には「リーチ格子」という謎の代数的な存在が登場し，いつの間にやら「保型形式」の計算をしていて，気づいたらなぜか接吻数が求まってしまった，という世にも奇妙なお話でした．

もちろん，収穫もありました．「なぜか $24$ 次元は接吻数が求まってしまう」という謎は，実はその半分の重さ $12$ の保型形式，すなわち「ラマヌジャンのデルタ」に関係している，ということもわかりました．いや〜，面白い！

これで， $24$ という数に愛着が湧いてきましたね！私の大好きな素数である $691$ も登場して，私は大満足です．

みなさんは楽しんでいただけたでしょうか．私はとても楽しかったです．

それでは今日はこのへんで．

参考文献

今回の記事は，英語版 Wikipedia が大変参考になりました！
Leech lattice - Wikipedia
Kissing number problem - Wikipedia

また，今回は $24$ 次元だけをご紹介しましたが，当然 $8$ 次元も気になるかと思います． $8$ 次元においては，「 $E_8$ 格子」と呼ばれるものが用いられるようです．詳しくはこちらをどうぞ．
E8 lattice - Wikipedia

格子の図はこちらのものをお借りしました．
格子 (数学) - Wikipedia

「接吻数問題」に関連する話題として「ケプラー予想」というものもあります．
ケプラー予想 - Wikipedia

「ケプラー予想」といえば，ジョージ・スピーロによる以下の関連書籍があります．私が最初に「接吻数問題」を知ったのはこの本でした．ただし，全部は読んでいません（幾何学の問題なのに，図がほとんどなくて・・・）．

ケプラー予想: 四百年の難問が解けるまで (新潮文庫―Science&History Collection)

作者: ジョージ・G.スピーロ,George G. Szpiro,青木薫
出版社/メーカー: 新潮社
発売日: 2013/12/24
メディア: 文庫
この商品を含むブログ (9件) を見る

リーチ格子については，これといってわかりやすい本はほとんど見たことがありません．強いて言えば，以下の本がありますが，あまりお勧めはしません．

「有限群」村の冒険―あなたは数学の妖精を見たことがありますか?

作者: 宮本雅彦,大石容子
出版社/メーカー: 日本評論社
発売日: 2006/07
メディア: 単行本
クリック: 4回
この商品を含むブログ (5件) を見る

tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

きっかけ

今回の記事は，鰺坂もっちょさんという方の考えた，以下の問題にインスピレーションを受けて書いています．よかったら，みなさんもぜひ考えてみてください．

C県は半径100kmの円である。花火の音は30km先まで届く。C県内の花火大会だけでC県全域に花火の音を行き渡らせるには、最低何箇所で花火大会を開催しなければならないか。
— 鯵坂もっちょ (@motcho_tw) 2016年8月6日

なるほどこれでも19になるのかあ pic.twitter.com/Eh2POl8jYy
— 鯵坂もっちょ (@motcho_tw) 2016年8月6日

念のため言っておくと，リーチ格子はもっちょさんの問題の解決には，（たぶん）まったく関係ありませんのでご注意ください．

*1:リーチ格子の最密性については，この論文で証明されているみたいです． [1603.06518] The sphere packing problem in dimension 24

*2:参考：Unimodular lattice - Wikipedia

*3:参考：Theta series of Leech lattice. - OEIS A008408 - OEIS

*4:コンウェイは，有名な数学者なので名前を聞いた人も多いかと思います。リーチ格子を使ってコンウェイ群を見つけたことでも知られています。

tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート