自由研究：アンモナイトの対数螺線 - tsujimotterのノートブック

８月は重たい記事ばかりかいてしまいましたが、今日は比較的さらっとした話をご紹介します。

2015年7月から開催の国立科学博物館の特別展「生命大躍進展」に行ってきました！<a href="http://www.seimei-ten.jp">生命大躍進展　人類誕生に至る40億年の壮大な生命進化の展覧会</a>www.seimei-ten.jp

地球上に酸素をもたらしたシアノバクテリアや、陸上に上がった両生類であるイクチオステガなど、生物の進化における「ターニングポイント」になった種に焦点をあてて、これらが具体的にどのような役割を果たしたのかを、実物の化石や迫力の再現映像を用いて紹介しています。生命が誕生してから現在に至るまでの地球のドラマがありありと感じられます。

特にCG映像は必見で、当時の最強と考えられているアノマロカリスが海中を勢いよく泳いで獲物を食らう様子など、さすがNHKというハイパークオリティで生き生きと描写されています。

10月4日までやっているそうなので、まだ行っていない方はぜひ足を運んでみてください。

個人的には大満足で、楽しんできたわけですが、テーマ的にはあまりこのブログっぽくないですね。

というわけで、今日のテーマは別のお話。

展示の途中で、tsujimotter はちょうど良いアンモナイト化石を見つけました。

アンモナイトがどうして「ちょうど良い」のか。

数学が好きなみなさんならわかりますよね。そう「対数螺(ら)線(せん)」です。

対数螺線とは、以下の極形式で表される曲線のことです。

$r(\theta) = a e^{b\theta}$

$a$ はただのスケールファクターなので、実際にいじらなければいけないパラメータは $b$ のみです。 $a = 1$ としておきましょう。

アンモナイトやオウムガイなどの巻貝の形状は、対数螺線を描くことが知られていますね。

ちなみに、なぜ対数螺線というかというと、 $b = 1$ として両辺自然対数をとると、

$\log(r) = \theta$

となって、中心からの距離 $r$ が角度 $\theta$ の自然対数でかけるからです。

今回は、アンモナイトの写真の上に対数螺線を載せることを試みたいと思います。というわけで、さっそく資料写真を撮影。

f:id:tsujimotter:20150819004111p:plain:w400

「プラティクリメニア」というアンモナイトの種の化石です。アスペクト比を変えないように、頑張って真上から撮りました。

対数螺線をこの画像に載せるための手順は以下の通りです。

Gnuplot で対数螺線を書く（この時点でざっくりパラメータを合わせる）。
画像として出力する。
パワーポイントで背景に写真を、その上に半透明化したプロット画像を載せてサイズを合わせる。
パラメータが合っていなければ 1. からやり直し。合っていれば次へ。
Mac の「プレビュー」を使って、背景を透明化する（これが地味に面倒）
再度画像を載せて微調整
できあがり

こうして出来上がった作品が、こちらです。

f:id:tsujimotter:20150819004428p:plain:w400

ドン！

どうですか？結構がんばったと思うのですが・・・。

図に書いてある通り、パラメータとしては $b = 0.16, \;\; 0\leq \theta \leq 29.0$ を用いています。

グラフの描画は以下の Gnuplot スクリプトを用いました。

# アンモナイトの対数螺旋
set polar
set size square
set sample 30000
set trange [0:29]

b = 0.16
r(t) = exp(b*t)
plot r(t) lw 3

やってみて分かったのですが、パラメータを合わせるのが思いのほか大変です。

数学の本には、アンモナイトや巻貝の構造は対数螺線になっていることがサラッと載っています。

たいてい疑いもせずに、適当に当てはめればすぐうまくいくものだと思い込んでしまうものですが、この曲線をうまく当てはめること自体なかなか難しいものなのです。

実際のところ、おそらくこの化石自体も、正確な対数螺線ではないはずです。理論的にはそうであっても現実のものは必ずしもその通りにはいかないものです。

また、パラメータは一意には定まりません。具体的に決めなければならないパラメータは $b$ １つですが、 $b$ を少々いじったところで、図形に劇的な変化はありません。また、曲線をフィットさせるポイントを変えれば、それっぽく見える曲線はいくらでも作れてしまいます。実際に、 $b = 1.4$ から $1.6$ くらいの間は、どれを選んでもうまく当てはまるような気がしてなりません。

結論としては、教科書に当たり前に書いてあることでも、やってみなければわからない、ということですね。

「夏休みの自由研究」みたいなまとめになってしまいました。笑

それでは今日はこの辺で。

参考

画像の背景を透過する方法はこちらを参考にしました。

[Mac] 「プレビュー」で簡単に画像の透明化が出来ます - rakuishi.com

アンモナイトの螺旋については、このサイトでかなり詳しく調べられています。

アンモナイトの螺旋を調べる

考察

Wikipedia によると、動径方向のベクトル $\bf{r}(\theta)$ と接線方向のベクトル $\bf{r}'(\theta)$ が成す角を $\alpha$ とし、この $\alpha$ を直角から引いた角のことをピッチというそうです。式としては以下で定義されます。

$\displaystyle \frac{\pi}{2} - \alpha = \frac{\pi}{2} - \frac{(\bf{r}, \bf{r}')}{|\bf{r}| |\bf{r}'|} = \arccos{\frac{b}{\sqrt{1+b^2}}}$

f:id:tsujimotter:20150819152610p:plain:w400

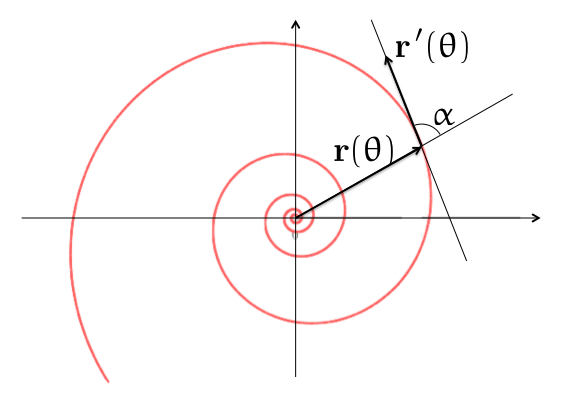
値はラジアンですが、度数法で計算すると $b = 0.16$ のとき $\alpha \approx 9.09$ ° ， $b = 0.14$ のとき $\alpha \approx 7.96$ ° となります。

参考までに、Wikipediaによるとオウムガイのピッチは 8° から 10° とのこと。アンモナイトのピッチの値としては、上の参考サイトでは『中心からの線と螺旋の接線とのなす角』の項目に $90° - \alpha$ の値が載っていて、いずれも 81° から 83° になっていますので、今回の結果は大きくは外れていないように思います。