先日、アフィンスキームについての3部記事を公開したところ、いろんな反応をいただきました。*1
tsujimotter.hatenablog.com
いただいたコメントの一つに、実は「層の射は、実は自然変換である」ということを教えてくれるものがありました。tsujimotterはこの事実を知らなかったのですが、勉強してみて面白いなと感じましたので、まとめてみたいと思います。
ちょうど今日がロマンティック数学ナイトプライム@圏論(略称:ロマ数プライム@圏論)というイベント開催日の前日ということで、圏論っぽい記事を書くにはちょうどよいタイミングかなと思いました。
romasucategorytheory.peatix.com
それではいってみましょう。
前層は関手
まず、前層の定義をおさらいしたいと思います。後のことを考えて、少し圏論的な用語を使って整理してみたいと思います。
位相空間 があるときに、
の開集合全体のなす圏
を考えます。
は
の開集合を対象とし、
の2つの開集合
の間に包含関係
があったときに
なる射を入れたものです。
このような の任意の開集合
に対して、
なる集合を与えるルール
を考えます。
2つの開集合 に対して
を考えます。
には、
における射
が入っているとすると、
から
への逆向きの写像
が与えられます。この
を
から
への制限写像といいます 。
このようにして与える が
から集合の圏
への反変関手であるとき、
のことを
上の前層といいます。
反変関手という用語が出てきましたので、ここで関手についてのおさらいをしておきましょう。
- 各対象
に対して
,
- 任意の射
および
に対して、
.
文章で書くとややこしいですが、図で書くとわかりやすいです。
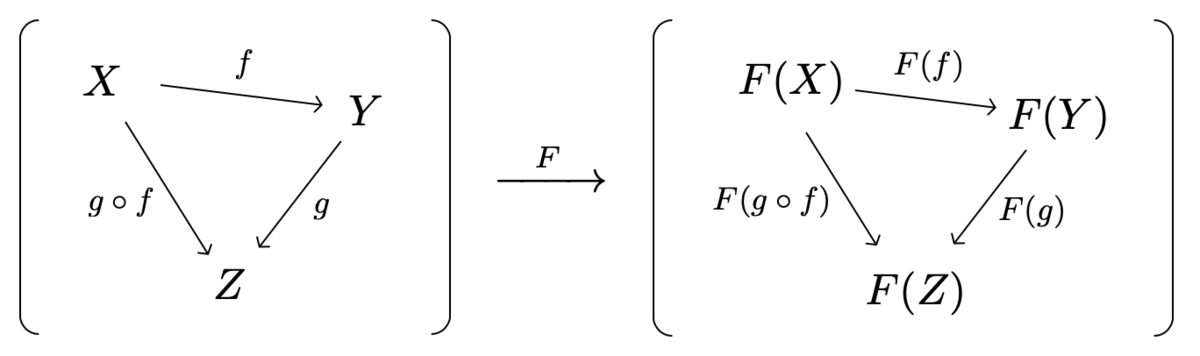
これに対して、定義域の圏 の射の向きをちょうど反転させた関手を反変関手といいます。
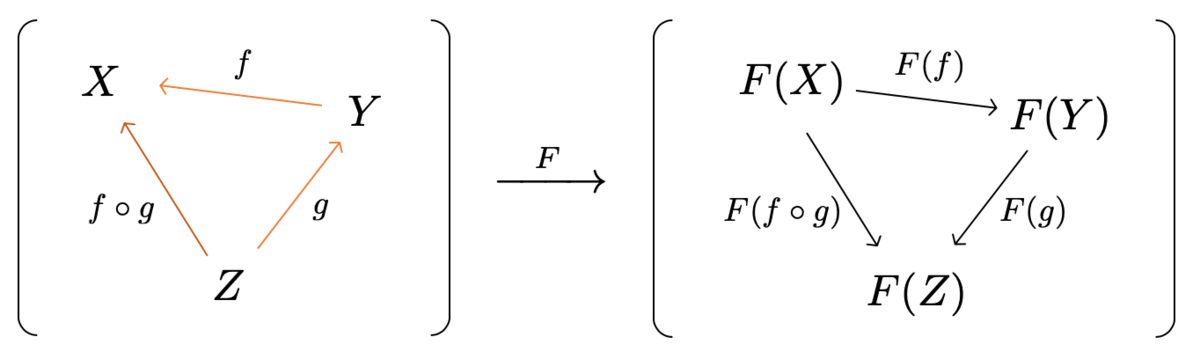
圏 の任意の射の向きを反転させた圏を
と表すことにすると、圏
から圏
への反変関手とは
から
への関手であると言い換えることもできます。
この視点でいうと、前層の定義を次のように言い換えることができますね。
この前層の中で、特別な性質をもったものが層と呼ばれるものです。
今回の記事では説明が面倒なのと、今回の本題にはさほど影響が出ないので、層の定義そのものには触れないことにしますが、興味がある人は参考文献に挙げた代数幾何の本などで調べてみてください。tsujimotterのノートブックでも、気が向いたら触れたいと思います。
なお、後で使うので言葉を定義しておくと、 上の層
に対して、
に対応する
のことを、層
の
における切断といいます。物騒ですが、数学用語です。
層の射は自然変換
層は関手であるという視点を手に入れたところで、いよいよ本題の 層の射 の話に移りたいと思います。
層の射の定義はアフィンスキームの記事の第3回で説明しましたが、もう一度思い出しましょう。
が成り立つもののことである。
これはすなわち、以下の可換図式が成り立つということである:

ただし、 はそれぞれ
の制限写像である。
層の射は、簡単に言ってしまえば、2つの層 のシステム(包含関係や制限写像)をうまく保ったまま、
の情報を
に移す写像のことです。
とはいえ、ちょっと定義が込み入っていますね。
層 は関手なので、それを意識して図を少し書き換えてみましょう。上で述べたように、
は
から
への関手です。
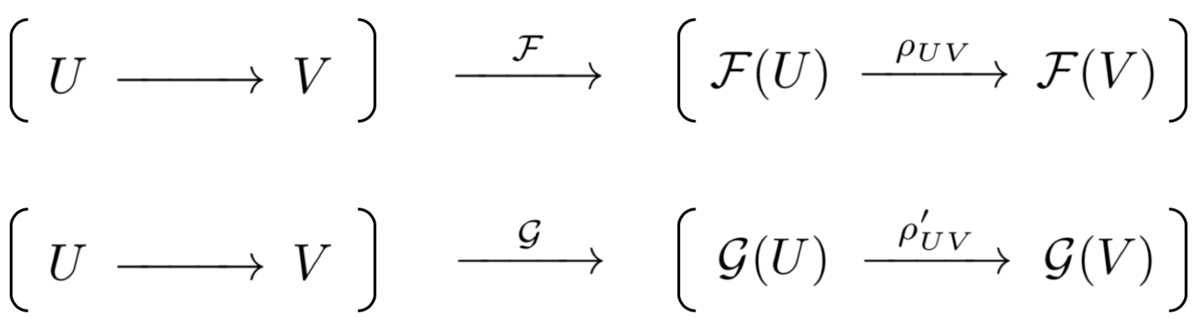
が共通なので、そのことを踏まえて図で表すと、次の
の図になります。
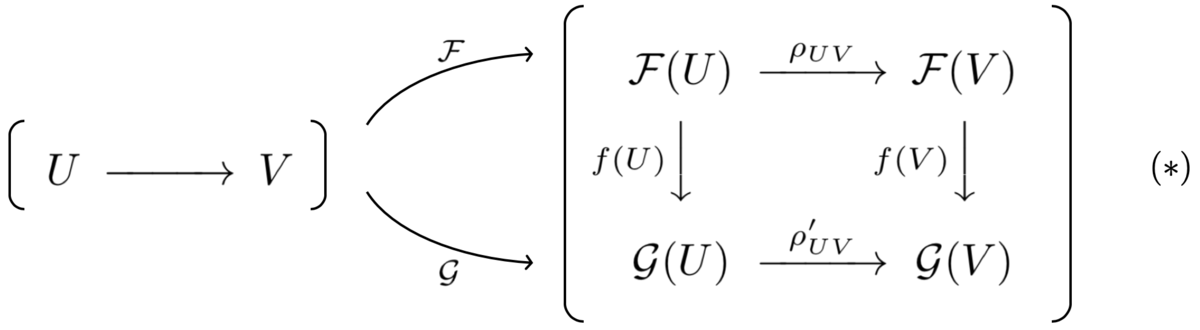
さて、ここまで層の射について説明してきました。一見込み入っていた層の射の定義ですが、実は圏論の言葉で述べると「自然変換である」というただ一言で表現することができます。そのことについて説明しましょう。
まず、自然変換の定義を思い出しましょう。自然変換とは、 が圏
の間の関手であるとき、
で映した情報を
に移し替えるルールのようなものです。圏から圏への射が関手であるように、自然変換は関手から関手への射に相当する概念です。*3
自然変換の定義を述べましょう。
が成り立つもののことである。
これはすなわち、以下の可換図式が成り立つということである:
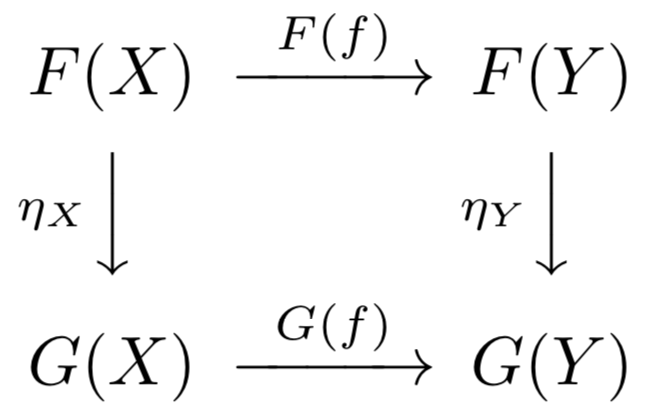
上の可換図式を見て、「おおっ」と感じませんか?
比較しやすいように、関手を意識して図を書き直すとこうなります。
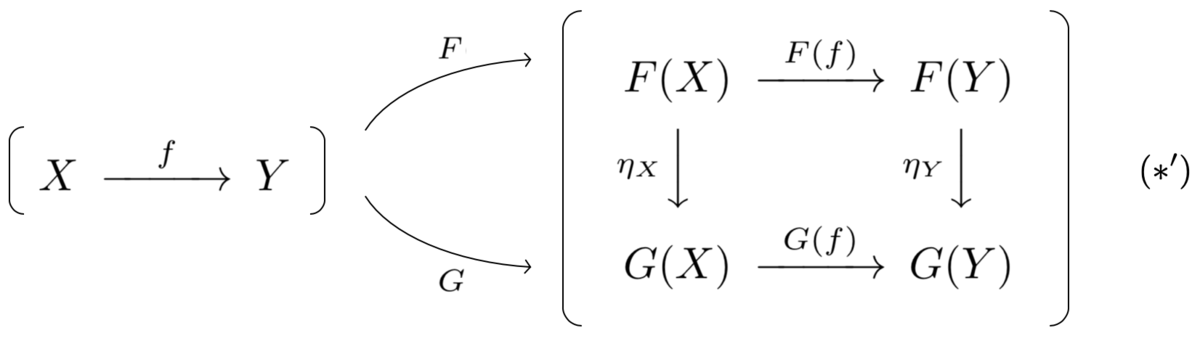
図 と図
を見比べてみてください。ぴったり対応していますね!
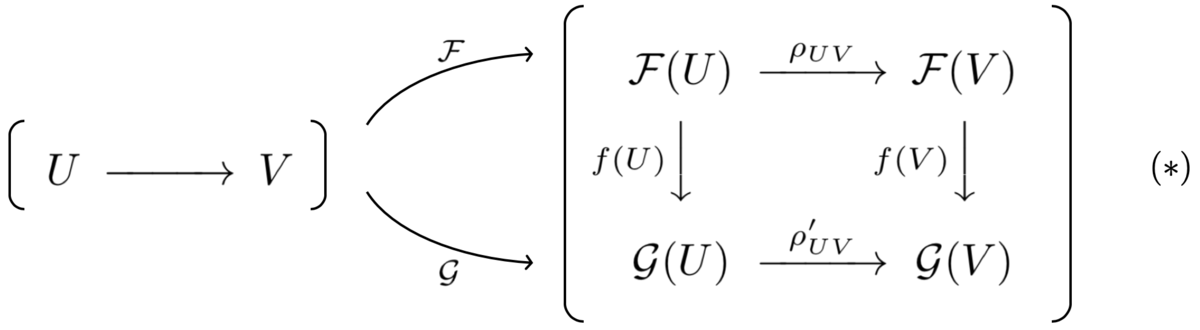

このことは、層の射はまさに自然変換であったことを表しています!なるほど!!
このような視点に立つと、 上の層
の間の射とは、関手
の間の自然変換である、ということができます。ややこしかった層の射の定義が、ずいぶんすっきり表現できましたね!
よくよく考えてみると、自然変換は関手と関手の間の射(関手圏と呼ばれる圏の射)なわけですから、前層が関手なのだとしたらその間の射は自然変換になりますよね。そう考えると、層の間の射の定義も、とても自然に感じられますね。
まとめ
今日は、ロマ数プライム@圏論の開催間近ということで、私なりの圏論との接点である「代数幾何学と圏論のつながり」についてまとめてみました。
(前)層とはまさに 関手 であり、層の間の射は 自然変換 そのものであることがわかりました。
tsujimotterにとっては、圏論はちょっとかじった程度で、なじみのない対象でしたし、関手や自然変換というワードは聞いたことがあっても、いったい何のためにそのような概念が必要になるのかはイメージできていませんでした。
しかし、こうして勉強してみると、関手とか自然変換は、まるで層のために生まれてきたんじゃないかと錯覚するぐらい、層を説明するのにぴったりな概念ですね。これは代数幾何やる人は圏論を勉強したくなるかもしれないですね。
縁がないと思っていた圏論との良い接点ができて嬉しいです。
抽象的な矢印だけで議論できるのは圏論の醍醐味だとは思うのです。一方で、今回のように、具体的な数学的対象を圏論の用語によってすっきり表現できる。そういった言語を提供しているというのも、圏論を学ぶの面白さの一つなんじゃないかなと思いました。
それでは今日はこの辺で。
参考

- 作者: R.ハーツホーン,高橋宣能
- 出版社/メーカー: 丸善出版
- 発売日: 2012/09/01
- メディア: 単行本
- この商品を含むブログを見る

- 作者: Tom Leinster,斎藤恭司,土岡俊介
- 出版社/メーカー: 丸善出版
- 発売日: 2017/01/29
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (3件) を見る