さぁ、後編です。前回の記事を読んでない方は、お先にこちらをどうぞ。
本エントリを最後まで読んでいけば「折り紙が3次方程式を折れるわけ」が理解できるはずです。
そしてあなたはこう思うことでしょう。
今後は、折り紙をみただけで、3次方程式を思い出すようになるかもしれません。笑
諸注意
今回は文章が非常に長いです。そして、前回と違い数式がたくさん出てきます!
しかしながら、扱う数式は高校の内容を超えません。よろしければ辛抱強くお付き合いくださいませ。
ちなみに、使用する高校数学の内容は次のものです。
- 放物線
- 点と点、点と直線の距離
- 二次関数
- 微分
上記について「ちょっと自信がないなあ」という方は、まずは話の流れだけでもおってみてください。
目標の再確認
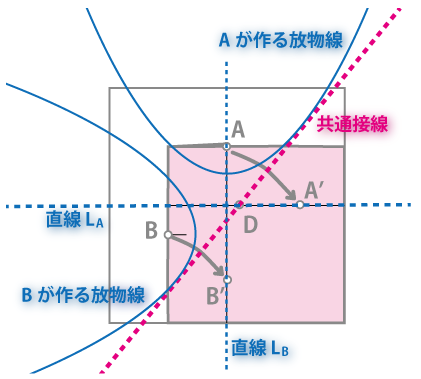
前編では、図の点 を直線に沿って折り重ねる「折り目の線」が、それぞれの点が作る放物線の接線に相当することを示しました。
そして、この2つの点を同時に重ねる操作は、2つの放物線の共通接線を求めることに相当することもわかりました。
今回は、これら放物線の数式を実際に計算します。その数式を使って、次に放物線の共通接線の式を求める。最後に、接線の傾きが「3次方程式の解の1つ」となることを示します。
まずは遊んで確認してみよう
『接線の傾きが「3次方程式の解の1つ」となることを示します』といっても、いきなり計算を始めてはイメージがわかりづらいと思います。
そこで、内容の雰囲気だけでもつかんでもらえるよう、体験型のブラウザアプリを作ってみました。
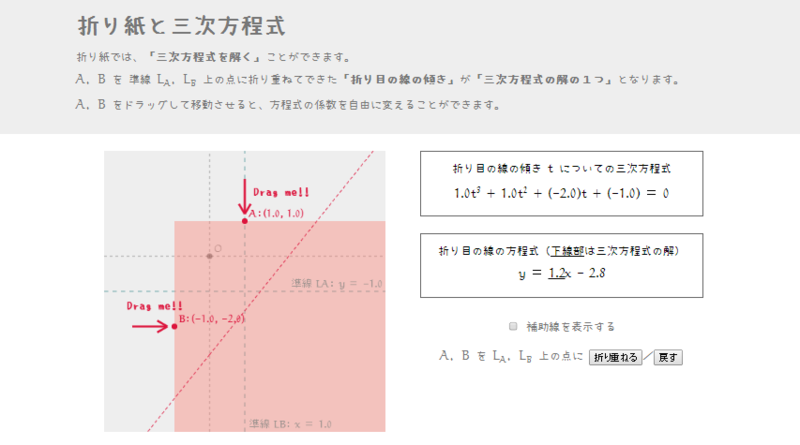
このアプリでは点 ,
の座標をマウスドラッグで自由に移動させることができます。点の移動に合わせて、対応する「放物線の形」やその「共通接線の傾き」が変化していきます。右側には現在の座標に対応する3次方程式が表示されますので、まさに点
,
の座標が3次方程式を作っている様子が分かるように作っています。
一通り遊んだら、数式による解法に取り掛かりたいと思います。
イメージはつかめましたか?
それでは3次方程式を目指して出発しましょう!
放物線を数式で表す
まずは、計算に必要な座標軸を図に追加してみましょう。
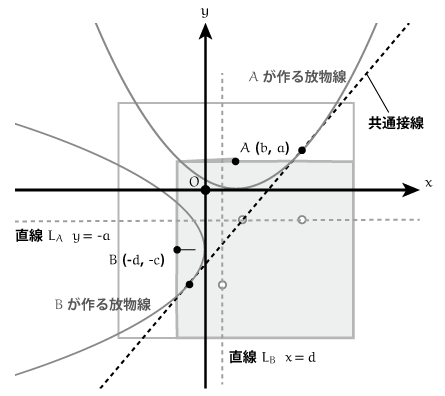
やりたいことは、図のそれぞれの放物線を を使った数式で表すことです。
このためには、ちょっと高校数学に立ち戻る必要があるでしょう。放物線の定義は、たしか・・・「数学C」で習うはずです。
高校の数学Cでは放物線は、次のように定義されます。
《放物線の定義》
準線と焦点から等しい距離にある点の軌跡
え?覚えてないって?
この際ですからいっそここで覚えてしまいましょう。
こういうことです。
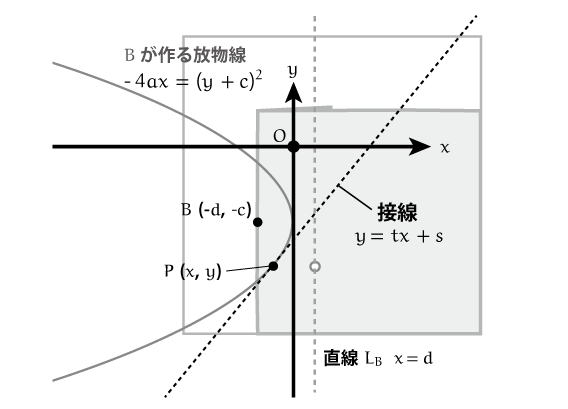
の作る放物線において、準線は
に相当します。焦点は点
のことです。
放物線上の点を とすると、《放物線の定義》から以下の式が成り立ちます。
《放物線の定義の言いかえ》
|点と焦点
の距離| = |点
と準線
の距離|
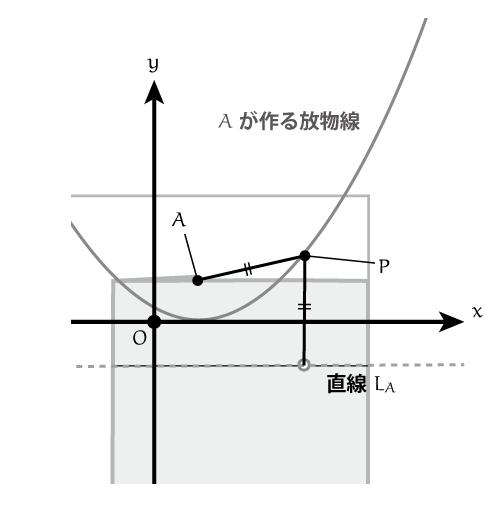
具体的に、放物線の軌跡を ,
の関係式として表してみましょう。
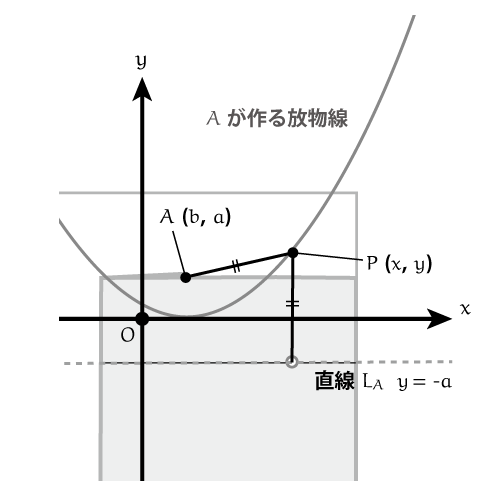
点 と 焦点
との距離は
一方、点 と 準線
との距離は
《放物線の定義の言い換え》 より両者が等しいから、次の式が成り立つ。
二乗すると、
展開すると、
さらに両辺変数消去すると、
移行して変形してみると、よりなじみがわくでしょう。
《放物線の式(点
に関して)》
結局のところ、数学1で習う二次関数とまったく同じ形の式になりますね。
点 によって作られる放物線も
,
を入れ替えて同様に考えることができます。
焦点の向きがマイナスになっている違う点に注意しましょう。
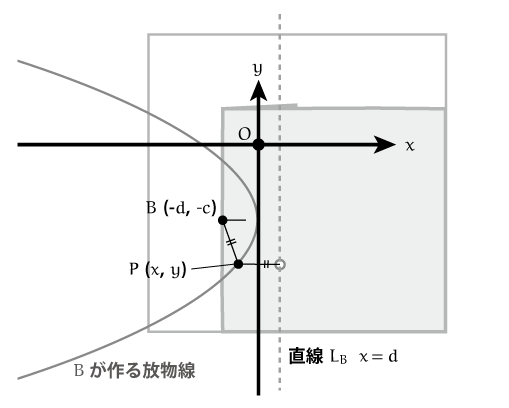
のときと同様に、図のように放物線上に点
を置きます。
点 は 焦点
, 準線
と等しい距離の点であることから、次の式が得られます。
《放物線の式(点
に関して)》
共通接線を求めるための方針
次は2つの放物線の共通接線の式を求めます。
とおいたときの ,
を求めることが狙いです。
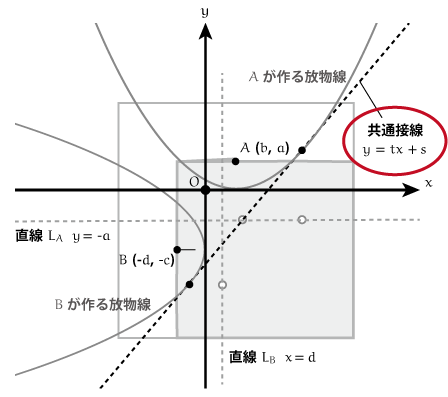
ところで、放物線が1つ決まったとしても、その接線の式は1つには決まりません。接線が通る点を決めることで ,
が1つに定まるわけです。
一方で、接線が通る点を決めなかったとしても ,
の値は全く自由に動き回るというわけではありません。放物線に接するという条件があるためです。
放物線に接する条件をつけると、点 の放物線からは、
と
の関係式が1本でてくるでしょう。同様に点
の放物線からも
と
の関係式が1本でてきます。
これらの接線が「共通」、すなわち、「等しい」わけですから、これらの式の連立方程式を解けば と
が具体的に求まるわけです。もちろん、ほしいのは共通接線の傾き
です。片方の式を代入することで
を消去してしまえばよいでしょう。
以上から、共通接線の傾き を決めるための、次のような方針が思いつきます。
- 接線の方程式を 変数
,
を用いて
とおく。
- 点
の放物線について、
,
に関する方程式が1本できる。
- 点
の放物線について、
,
に関する方程式が1本できる。
- 2つの方程式を連立させて変数
を消去すると、《共通接線の傾き
に関する方程式》が完成する。この式が3次方程式になる(といいな)。
さて、方針が決まったので一気に計算してみましょう。
点  について
について  ,
,  に関する方程式をつくる
に関する方程式をつくる
接線 が放物線
に接する点を
とおきます。
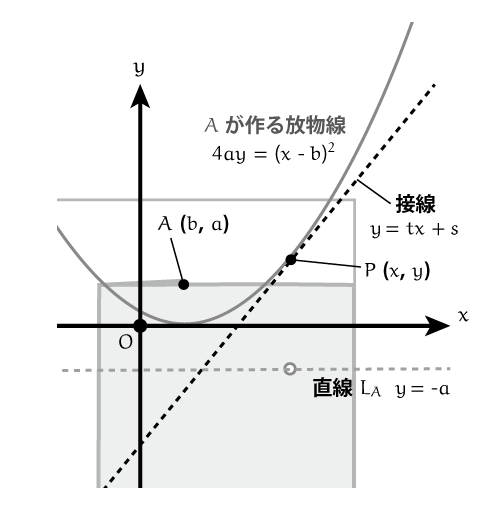
放物線の式 の両辺を
で微分すると、
接線の傾き は 微分係数
と等しいから
一方、点 は放物線上の点より、以下の式を満たすはずです。
(式2) を に代入すると
ここで接線の方程式
これにより ,
が消去されて、
と
の方程式が得られました。
《点
についての
,
に関する方程式》
点  について
について  ,
,  に関する方程式をつくる
に関する方程式をつくる
接線 が放物線
に接する点を
とおきます。
放物線の式を で微分すると
接線の傾き は微分係数
と等しいから
一方、点 は放物線上の点より、以下の式を満たすはずです。
(式5) を に代入すると
ここで接線の方程式
これにより ,
が消去されて、
と
の方程式が得られました。
《点
についての
,
に関する方程式》
《共通接線の傾き  に関する方程式》をつくる
に関する方程式》をつくる
最後の仕上げです。
以上2つの式をまとめると、こうなります。
ここで、(式7) の に (式4) を代入します。
両辺に をかけましょう。
ついに出ました!これこそ、求めていた「3次方程式」ですね!
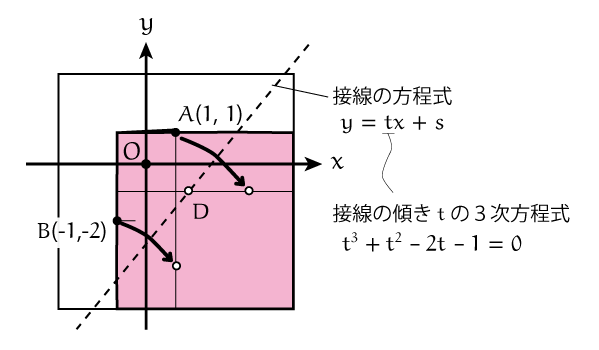
《共通接線の傾き
の方程式》
任意の3次方程式を作れるか?
もちろん Yes! です。
(式8)を見れば明らかですが、都合のいいことに方程式のすべての係数は、点 ,
の
座標である、
というパラメータに1対1で対応しています。
点 ,
は二次元平面上の任意の点に置くことができます。したがって、任意の係数の3次方程式を作ることができるわけです*1。もちろんそれぞれが負になっても構いません。
ただし、この方程式の解は「接線の傾き」に対応しますので、折り紙を折って得られる解は当然「実数解」に限ります。3次方程式は、最大3つの実数解をもちますので、共通接線は最大3つ存在することになります。その場合、折り紙によって得られるものは、そのうちの1つの解に対応した共通接線です。
また、3次方程式には必ず1つの実数解を持つことが保証されていますので、共通接線は必ず存在します。どんな をとったとしても、共通接線は存在するわけです。
ここで、正七角形の折り紙に話を戻すと、座標は ,
となり、方程式の係数は
,
,
,
です。
得られる方程式は、次の式になります。
《共通接線の傾き
の方程式(正七角形の場合)》
この式の1つの実数解は、次のものです。
ここで簡単に示すことができませんが、この解は2次以下の方程式で作ることはできず、なおかつ正七角形を作るのに必須です。
折り紙に対して引き合いに出される「定規とコンパスの作図」では、2次方程式を解くことが限界です。
したがって、正七角形を厳密に作図するには、「定規とコンパス」ではなく「折り紙」を使う必要があるのです。
まとめ
前編と後編(本エントリ)の2回に渡って「折り紙が3次方程式を折れるわけ」について解説してきました。
前編では、3次方程式の準備段階として、点を線に折り合わせることの図形的な意味を考えて、次の2つの結論を得ました。
- 焦点を準線に沿って折り重ねる「折り目の線」は、それぞれの点が作る放物線の接線に相当する。
- 放物線を作る操作を2組の焦点・準線の組に同時に行うと、それぞれの放物線の共通接線ができる。
後編の本エントリをまとめると、次の3点の内容になるかと思います。
- 共通接線の傾きは、3次方程式の解の1つになる。
- 3次方程式の係数は、焦点の座標や準線の方程式を使って表せる。
- 焦点の座標や準線の方程式を変更することで、任意の3次方程式を求めることができる。
「点を直線に折り重ねることが出来る」という折り紙の持つたったそれだけの特徴で、3次方程式という複雑な数式も解くことができるなんて驚きですね。
折り紙のすごさをわかっていただけたら幸いです。
参考文献
前回と今回のエントリは、解説はtsujimotterのオリジナルですが、基本的な考え方は次の本にのっとっています。この本は、折り紙の数学的な取り扱いについて、体系的に書かれた最も充実した本だと思います。
基礎から応用まで、非常に興味深い内容がたくさん詰まっていますので、本エントリを見て興味を持った方はぜひ手に取って(クリックして)いただけると幸いです。

- 作者: ロベルトゲレトシュレーガー,Robert Geretschl¨ager,深川英俊
- 出版社/メーカー: 森北出版
- 発売日: 2002/04
- メディア: 単行本
- クリック: 2回
- この商品を含むブログ (1件) を見る
*1:正確にいえば「折り紙の他の操作によって、任意の有理数の点を作ることができるため、任意の有理係数の3次方程式を作ることができる。」です。