p進L関数とクンマーの合同式 - tsujimotterのノートブック

ゼータ関数

$\displaystyle \zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^s}$

の負の整数 $s = -1, -2, -3, \ldots$ における値には面白い性質があります。

たとえば， $s = -31$ の値は

$\displaystyle \zeta(-31) = \frac{37\cdot 683 \cdot 305065927}{2^6 \cdot 3 \cdot 5 \cdot 17}$

となって $37$ で割り切れますが， $s = -67$ の値は

$\displaystyle \zeta(-67) = \frac{37\cdot 101 \cdot 123143 \cdot 1822329343 \cdot 5525473366510930028227481}{2^3 \cdot 3 \cdot 5}$

となり，どちらも $p = 37$ で割り切れます。

ほかにも無数の $\bmod{p}, \bmod{p^2}, \bmod{p^3}, \ldots$ に関する合同式を立てることができ，これらをまとめたものがクンマーの合同式です。あとで詳細は紹介しますが，クンマーの合同式は，簡単にいえば $r \equiv r' \pmod{p^n}$ のときに $\zeta(1-r), \zeta(1-r')$ に対して $\pmod{p^{n+1}}$ の合同式が成り立つことを主張する定理です。言い換えれば $r, r'$ がp進的に近ければ， $\zeta(1-r), \zeta(1-r')$ もp進的に近いことを表しています。ゼータ関数の特殊値に存在する「p進的な性質」を示唆していると言えます。

この辺のお話は「ゼータ関数の左側」の性質として，数学カフェでも紹介したことがありました。以下のスライドにまとめているのでご覧になってください。

クンマーの合同式とゼータ関数の左側 - 数学カフェ #mathcafe_height from Junpei Tsuji

www.slideshare.net

前々回の記事で紹介した岩澤理論では，ゼータ関数の持つこのような「p進的な性質」について，その根拠を与えてくれます。実はゼータ関数の背後には「p進L関数」という，p進的な性質を持った関数が存在して，p進L関数の性質がゼータ関数の特殊値に遺伝することによってクンマーの合同式が成り立っているのです。今日はこれについて解説しましょう。

p進L関数について考える前に，ゼータ関数の（ある種の）一般化である「L関数」について述べておきましょう。

定義：L関数

原始的Dirichlet指標 $\chi \colon \mathbb{Z} \to \mathbb{C}$ に対して，L関数を次式で定義する：

$\displaystyle L(\chi, s) = \sum_{n=1}^{\infty}\frac{\chi(n)}{n^s}$

上記の級数は $Re(s) > 1$ で絶対収束する．全複素平面に有理型に接続され， $\chi \neq \mathbf{1}$ ならば全複素平面で正則となる．

Dirichlet指標の箇所を無視すれば，ほぼゼータ関数と同じ形をしています。実際 $\chi = \mathbf{1}$ （自明な指標）とすると， $L(\mathbf{1}, s)$ はゼータ関数 $\zeta(s)$ に一致します。

L関数を用いると，クンマーの合同式は以下のように定式化されます。

$r \equiv r' \pmod{p^n}$ なる正の整数 $r, r'$ に対して

$\displaystyle \begin{align*} &\left(1 - \frac{(\psi \omega^{-r})(p)}{p^{1-r}}\right)L(\psi \omega^{-r}, \; 1-r) \\ &\equiv \left(1 - \frac{(\psi \omega^{-r'})(p)}{p^{1-r'}}\right)L(\psi \omega^{-r'}, \; 1-r') \pmod{p^{n+1}} \end{align*}$

が成り立つ．

ここで $\psi$ は，導手が $Np^e$ （ $N$ は $p$ と素な自然数， $e = 0$ または $e = 1$ ）で， $\psi(-1) = 1$ なる原始的Dirichlet指標とします。

細かいことを除けば， $s = 1-r$ のL関数の特殊値 $L(\chi, 1-r)$ と $s = 1-r'$ の特殊値 $L(\chi, 1-r')$ との間に成り立つ $\bmod{p^{n+1}}$ における合同関係を表しています。

なお，本記事の内容は，岩澤理論とその展望（上）という本を参考にしています。本書では，p は 3 以上の素数としているので，本記事でもこれを前提とします。

岩澤理論とその展望(上) (岩波数学叢書)

作者:落合理
岩波書店

Amazon

合同式についての補足

この節は，わかっている人は読み飛ばしてもらってかまいません。

上の「クンマーの合同式」をはじめとしたいくつかの合同式ですが，はじめて見た方はびっくりするかもしれません。いわゆる普通の合同式は $a, b \in \mathbb{Z}$ として

$a \equiv b \pmod{p^n}$

の形をしたものでした。今回の合同式は， $a, b$ が整数ではありません。ゼータ関数のケースでは「有理数同士の合同式」になっています。このような合同式はどうやって定義されるのでしょう。

$\mathbb{Z}$ における，通常の意味の合同式 $a \equiv b \pmod{p^n}$ は，両辺の差 $a-b$ が $p^n$ で割り切れることを指します。これは「 $a-b$ が $\mathbb{Z}$ のイデアル $p^n\mathbb{Z}$ に属する」のように言い換えることができます。

有理数同士の場合も同様に考えますが，この場合は $\mathbb{Z}_p$ での合同式を考えます。つまり， $a, b \in \mathbb{Z}_p$ における合同式 $a \equiv b \pmod{p^n}$ は， $a-b$ が $\mathbb{Z}_p$ のイデアル $p^n\mathbb{Z}_p$ に属するとして定義されます。有理数体 $\mathbb{Q}$ は $\mathbb{Z}_p$ に埋め込まれますから，ゼータの合同式は $\mathbb{Z}_p$ の合同式として考えられるわけです。L関数の場合は，ディリクレ指標 $\chi$ の値が係数につきますから， $\mathbb{Z}_p$ に $\chi$ の値を加えた環を考えます。これについては次節で再度注意します。

さて，こういう風にいうと，ややこしく思えるかもしれませんが実はそんなに難しいものではありません。 $a, b \in \mathbb{Q}$ のとき， $a \equiv b \pmod{p^n}$ という合同式は， $a - b$ の既約分子（約分したときの分子）を $p^n$ が割り切ると言い換えてもよいのです。先ほどの例であれば，

$\zeta(-31) - \zeta(-67)$

を計算して約分して，その分子が $37$ の倍数であるかどうか確認すればいいのです。

慣れるまで少しややこしく感じるかもしれませんが，ぜひいろいろな例で試してみてください。

p進L関数の補間性質

まずは，p進L関数を定義しましょう。この辺から岩澤理論に関する話が登場しますので，前々回の記事をあらかじめご参照ください。
tsujimotter.hatenablog.com

上の記事では，岩澤代数 $\newcommand{\zp}{\mathbb{Z}_p}\newcommand{\cyc}{{\mathrm{cyc}}} \Lambda_{\cyc} = \zp[[\Gamma_{\cyc}]]$ と呼ばれるものが登場していました。この岩澤代数は， $\mathbb{Q}$ 上の円分 $\zp$ 拡大のガロア群 $\Gamma_{\cyc} = \mathrm{Gal}(\mathbb{Q}_{\infty}/\mathbb{Q})$ についての完備群環です。前回はもう少し一般の $\zp$ 拡大を考えていましたが，今回の記事では $\mathbb{Q}$ 上の円分 $\zp$ 拡大のみを考えます。

今回の記事では，前回用いた岩澤代数 $\Lambda_{\cyc}$ より係数環がもう少しだけ大きくなったもの

$\newcommand{\iwasawa}{{\Lambda_{\cyc, \psi}}} \iwasawa = \zp[\psi][[\Gamma_{\cyc}]]$

を考えます。

$\mathbb{Z}_p [\psi]$ は， $\psi$ を $\psi \colon \mathbb{Z} \to \mathbb{C}$ なる Dirichlet 指標として， $\mathbb{Z}_p$ に $\psi$ の値を付け加えて得られる $\overline{\mathbb{Q}}_p$ の部分環を表します。

このとき，久保田-Leopoldt，岩澤，Colemanらによって次の結果が得られています。主張の中身が少し長いので，主張を述べたあとで説明を加えたいと思います。

定理：p進L関数の補間性質

$\psi$ を導手が $Np^e$ （ $N$ は $p$ と素な自然数， $e = 0$ または $e = 1$ ）で， $\psi(-1) = 1$ なる原始的Dirichlet指標とする．このとき，

$\displaystyle L_p(\psi) \in \begin{cases} \iwasawa & \psi \neq \mathbf{1}, \\ \frac{1}{\gamma - \kappa_{\cyc}(\gamma)}\Lambda_{\cyc} & \psi = \mathbf{1} \end{cases}$

が一意に存在して，任意の整数 $r \geqq 1$ と $\overline{\mathbb{Q}}_p^\times$ に値を持つ $\Gamma_{\cyc}$ の任意の有限指標 $\phi$ に対して， $\overline{\mathbb{Q}}_p$ における等式：

$\displaystyle \kappa_{\cyc}^{1-r} \phi(L_p(\psi)) = \left(1 - \frac{(\psi \omega^{-r}\phi^{-1})(p)}{p^{1-r}}\right)L(\psi \omega^{-r} \phi^{-1}, \; 1-r)$

を満たす．ただし， $\gamma$ は $\Gamma_{\cyc}$ の位相的生成元であり， $\psi = \mathbf{1}$ のときは $r\neq 1$ または $\phi \neq \mathbf{1}$ と仮定する．

また， $\phi^{-1}$ は十分大きな $n$ が存在して， $\newcommand{\gal}{\mathrm{Gal}} \gal(\mathbb{Q}(\mu_{p^n}) / \mathbb{Q})$ の指標とみなせるので， $\gal(\mathbb{Q}(\mu_{p^n}) / \mathbb{Q}) \simeq (\mathbb{Z}/p^n\mathbb{Z})^\times$ の同型を通して自然に Dirichlet 指標とみなしていることに注意する．

いろいろ定義していない記号が出てきて申し訳ありませんが， $\omega, \kappa_{\cyc}$ はそれぞれTeichmüller指標，円分指標と呼ばれる重要な指標です。 $\gamma \in \Gamma_{\cyc}$ は $\Gamma_{\cyc}$ の位相的生成元です。

定理の主張の前半と後半の２つに分けて考えましょう。便宜上，以降の説明では $\psi \neq \mathbf{1}$ とします。

まず，前半で述べたことは，ある特別な元 $L_p(\psi)$ が岩澤代数 $\iwasawa$ の中に存在して，一意に定まるということです。一意に定まるので，これを「p進L関数」と名付けようというわけです。

なぜ「p進L関数」なのかについては，後半の主張でわかります。後半では， $L_p(\psi)$ に円分指標と有限指標 $\phi$ の２つのDirichlet指標の積 $\kappa_{\cyc}^{1-r}\phi$ を適用すると，L関数の特殊値 $L(\psi \omega^{-r} \phi^{-1}, \; 1-r)$ と結びつくことを主張しています。 $\kappa_{\cyc}^{1-r}$ の $1-r$ の箇所は，一般に $s \in \zp$ として $\kappa_{\cyc}^s$ とすることができます。

$\kappa_{\cyc}^s \phi(L_p(\psi))$

$s = 1-r$ （ $r$ は正の整数）のときに限りL関数の特殊値と一致しますが，このような性質を補間性質と言います。 $s \in \zp$ におけるp進L関数の値は， $s = 0, -1, -2, -3, \ldots$ の値を補間するように定まるというわけですね。まさにp進L関数。

ここで $s = 1-r$ のときの値としては，単純にL関数が出てくるのではなく，

$\displaystyle \left(1 - \frac{(\psi \omega^{-r}\phi^{-1})(p)}{p^{1-r}}\right)$

という余分な因子が現れます。この逆数をEuler因子といい，L関数のEuler積における $p$ に関する因子と一致します。すなわち，pに関するEuler因子の逆数をかけることによって，pに関するEuler因子をあらかじめ相殺しておく必要があるということです。それ以外の部分についてはL関数そのものです。

以上をまとめると，p進L関数は以下の３点によって特徴付けられます。

岩澤代数 $\iwasawa$ の一意に定まる特別な元であり
$s \in \zp$ に対して $\kappa_{\cyc}^{s}\phi$ を適用すると $\overline{\mathbb{Q}_p}^{\times}$ の値をとるp進的な関数であり
特に $s = 1-r$ においては，（Euler因子を除いて）L関数の特殊値と一致する

このようなp進L関数は，以下の２通りの方法によって具体的に構成することができます。

Stickelberger元を用いた方法（岩澤）
円単数のノルム系を用いた方法（Coleman）

それぞれまったく異なる構成方法にもかかわらず，上の補間性質を持つp進L関数を作り出すことができるのです。このことは，p進L関数の多面性を表していて，これによって岩澤主予想（Iwasawa Main Conjecture）が２通りの方法で証明することができたりするなど，さまざまな利点が生まれます。

補間性質の証明は残念ながらここでは書きません。まだ私がちゃんと理解していないためです。いずれこのブログでも書きたいと思っていますが。

以上により，p進L関数という岩澤代数の元が存在することがわかりました。以前の記事で紹介した通り，岩澤代数は，セールの同型によって「べき級数」とみなすことができるのでした。岩澤類数公式の証明においても，このような考え方の転換は大活躍しましたが，今回も同様です。

位相的生成元 $\gamma$ として特に $\kappa_{\cyc}(\gamma) = 1 + p$ なる $\gamma \in \Gamma_{\cyc}$ をとり，同型写像

$\begin{align*} \iwasawa &\xrightarrow{\; {\simeq} \; } \zp[\psi] [[T]], \\ \gamma &\longmapsto 1 + T \end{align*}$

を固定します（セールの同型）。このとき次の可換図式があります：

このことはすぐ確かめられます。

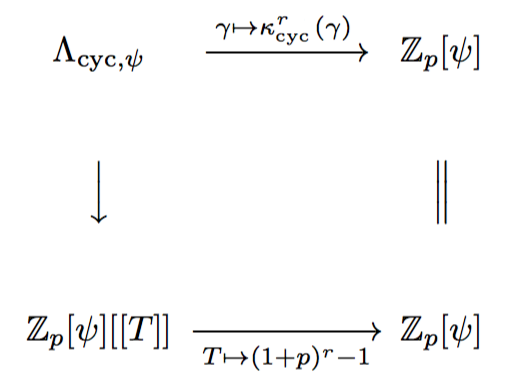
右回りの経路は $\gamma$ に $\kappa_{\cyc}^{r}$ を適用しています。 $\kappa_{\cyc}(\gamma) = 1 + p$ より， $\kappa_{\cyc}^r(\gamma) = (1 + p)^r$ となります。

また，左回りの経路は $\gamma$ に $\gamma \mapsto 1+T$ を適用してから $T \mapsto (1+p)^r - 1$ を適用しています。合成すると $\gamma \mapsto (1 + p)^r$ となって右回りの経路と一致します。

以上の考え方により，岩澤代数 $\iwasawa$ の元 $L_p(\psi)$ を，べき級数 $A(T) \in \zp[\psi][ [T] ]$ として考える意味が出てきます。

べき級数の合同式

上記で考えたべき級数 $A(T)$ には，以下の補題で主張されるような合同式が成り立ちます。この補題がクンマーの合同式を示すための，もう一つのキーになります。

補題：べき級数の合同式

勝手な元 $A(T) \in \mathbb{Z}_p[\psi] [[ T ]]$ をとる． $r\equiv r' \pmod{p^n}$ とすると，

$A(T)\big|_{T=(1+p)^r-1} \equiv A(T)\big|_{T=(1+p)^{r'}-1} \pmod{p^{n+1}}$

が成り立つ．

だんだん，クンマーの合同式に近づいてきた感じがしますね。実際あと一歩です。

この補題の証明は，二項展開を用いることになります。私が参考にしている「岩澤理論とその展望（上）」の補題3.31に相当するものですが，証明が省略されてよくわかりませんでした。なんとか，自分なりに証明をつけることができましたので，それを以下に記します。

裏話をすると，二項係数の合同式についての証明は，自分一人ではできませんでした。Twitterで尋ねたところ，のらんぶるさんという方から答えを教えていただきまして，なんとかこのようにまとめることができました。

基本的には $(1+p)^r$ の二項展開と合同式の性質を使うことで証明できます。ただ， $r$ は負の整数値も取るので注意が必要です。

$\newcommand{\ord}{{\mathrm{ord}}} \ord_p(k!)$ という記号について補足をしておきます。 $\ord_p(n)$ はp進付値と呼ばれる写像 $\mathbb{Q}_p \to \mathbb{Z}$ で， $n$ を $p$ が何回割り切るかを表す記号です。たとえば， $\ord_3(18)$ であれば $18 = 2\cdot 3^2$ を $3$ が $2$ 回割り切りますので， $\ord_3{18} = 2$ です。

仮定より $r \equiv r' \pmod{p^n}$ から，

$r(r-1) \cdots (r-k+1) \equiv r'(r' - 1) \cdots (r'-k+1) \pmod{p^n}$

が得られる．両辺を $k!$ で割ると， $\ord_p(k!)$ の分だけずれるので

$\displaystyle \frac{r(r-1) \cdots (r-k+1)}{k!} \equiv \frac{r'(r' - 1) \cdots (r'-k+1)}{k!} \pmod{p^{n - \ord_p(k!)}}$

が成り立つ．

したがって，一般化された二項係数の定義

$\displaystyle \binom{r}{k} := \frac{r(r-1) \cdots (r-k+1)}{k!}$

より

$\displaystyle \binom{r}{k} \equiv \binom{r'}{k} \pmod{p^{n- \ord_p(k!)}} \tag{1}$

が成り立つ．

$p\geqq 3$ より， $k > 0$ のとき

$\displaystyle \ord_p(k!) < \frac{k}{p-1}$

が成り立つので（数論Ⅱの第10章問３より）

$\displaystyle \ord_p(k!) < \frac{k}{p-1} \leq k - 1$

が得られる．よって，

$\displaystyle \binom{r}{k} \equiv \binom{r'}{k} \pmod{p^{n-k+1}}$

が成り立つ． $p^k$ をかけると

$\displaystyle \binom{r}{k}p^k \equiv \binom{r'}{k}p^k \pmod{p^{n+1}} \tag{2}$

が成り立つ．

以上を用いて $(1+p)^r - 1$ の二項展開を計算する．

$\begin{align*} (1+p)^r - 1 &= \left( 1 + \binom{r}{1}p + \binom{r}{2}p^2 + \cdots \right) - 1 \\ &\equiv \binom{r}{1}p + \binom{r}{2}p^2 + \cdots + \binom{r}{n}p^n \\ &\equiv \binom{r'}{1}p + \binom{r'}{2}p^2 + \cdots + \binom{r'}{n}p^n \\ &\equiv (1+p)^{r'} - 1 \pmod{p^{n+1}}\end{align*}$

となる．

$A(T) \in \mathbb{Z}_p[\psi][[T]]$ は， $a_0, a_1, a_2, \ldots \in \mathbb{Z}_p [\psi]$ として一般に

$A(T) = a_0 + a_1 T + a_2 T^2 + \cdots$

とかける．ここで $T = (1+p)^r - 1$ とすると

$\begin{align*} A(T)\big|_{T = (1+p)^r - 1} &= a_0 + a_1 \left\{(1+p)^r-1\right\} + a_2 \left\{(1+p)^r-1\right\}^2 + \cdots \\ &\equiv a_0 + a_1 \left\{(1+p)^{r'}-1\right\} + a_2 \left\{(1+p)^{r'}-1\right\}^2 + \cdots \\ &\equiv A(T)\big|_{T = (1+p)^{r'} - 1} \pmod{p^{n+1}} \end{align*}$

となり補題が証明される．

※ 次節のクンマーの合同式の導出のためには $r < 0$ のケースのことを考える必要があることに気づきました。二項係数の議論を修正する必要があります。近いうちに修正します。 → 修正しました！

クンマーの合同式の導出

以上を用いるとクンマーの合同式を導くことができます。ここでは， $\psi \neq \mathbf{1}$ のときだけを考えます。

$r$ を $1-r$ に置き換えて先ほどの可換図式を考える．この可換図式において①右回り②左回りの２通りの経路を考えたい．

まず，①右回り

$\iwasawa \xrightarrow{\gamma \mapsto \kappa_{\cyc}^{1-r}(\gamma)} \zp[\psi] \left( \subset \overline{\mathbb{Q}_p}\right)$

の経路を，p進L関数 $L_p(\psi) \in \iwasawa$ に対して適用すると，p進L関数の補間性質の式において $\phi = \mathbf{1}$ としたもの

$\displaystyle L_p(\psi) \; \longmapsto \; \left(1 - \frac{(\psi \omega^{-r})(p)}{p^{1-r}}\right)L(\psi \omega^{-r}, \; 1-r)$

と一致する．これはL関数の特殊値であった．

一方，②左回り

$\iwasawa \xrightarrow{\gamma \mapsto 1 + T} \zp[\psi] [[T]] \xrightarrow{T \mapsto (1+p)^{1-r} - 1} \zp[\psi]$

の経路は，セールの同型によってべき級数 $A(T) \in \zp[\psi] [[T]]$ に移してから， $T$ に $(1+p)^{1-r} - 1$ を代入することを意味する．

$L_p(\psi) \; \longmapsto \; A(T) \; \longmapsto \; A(T)\big|_{T=(1+p)^{1-r} - 1}$

これらの２つが可換であることから，下の経路で得られるベキ級数 $A(T)$ に $T = (1+p)^{1-r} -1$ を代入して得られた $\zp[\psi]$ の値も，L関数の特殊値と一致する．

したがって

$\displaystyle A(T)\big|_{T=(1+p)^{1-r} - 1} = \left(1 - \frac{(\psi \omega^{-r})(p)}{p^{1-r}}\right)L(\psi \omega^{-r}, \; 1-r)$

が成り立つ．

また $r \equiv r' \pmod{p^n}$ ならば $1-r \equiv 1-r' \pmod{p^n}$ であるから，補題より $A(T) \in \zp[\psi] [[T]]$ に $T = (1+p)^{1-r} - 1$ と $T = (1+p)^{1-r'} - 1$ をそれぞれ代入して得られた値の間には， $\bmod{p^{n+1}}$ において合同関係が成り立つ．

したがって， $r \equiv r' \pmod{p^n}$ なる正の整数 $r, r'$ に対して

なる合同式が成り立つことがわかる．これは，クンマーの合同式そのものである．

まとめ

今日は岩澤理論の記事第二弾として「p進L関数」についてご紹介しました。

p進L関数という「岩澤代数における都合のよい元」が存在すれば，補間性質によりクンマーの合同式という「ゼータ関数のp進的性質」を導くことができるというお話でした。p進L関数の具体的な構成は一段と難しいですが，またの機会にチャレンジしたいと思います。

岩澤理論の研究集会 Iwasawa2017 は今週の水曜から始まりますね。Twitterの情報によると，岩澤理論の専門家の先生が続々と来日しているそうです。

それでは，今日はこの辺で！

疑問（解決）

途中で現れた可換図式で $\gamma \mapsto \kappa^{1-r}_{\cyc}(\gamma)$ と書いていますが，参考文献の方には $\gamma \mapsto \kappa^{r}_{\cyc}(\gamma)$ となっていました。これは私の勘違いなのか，はたまた誤植なんでしょうか。