部分分数分解の公式 - tsujimotterのノートブック

Twitterを眺めていると、とても楽しいツイートが流れてきました。

部分分数分解のこのテクニックなんだ。

知らなかった。 pic.twitter.com/DwfFX3JSB4
— やまごえ@情数教育 (@awellbottom) 2018年4月23日

部分分数分解のテクニックだそうです。私も知りませんでした！

$\displaystyle \frac{1}{(s+1)(s+2)}$

という多項式の積で書かれた分数を、 $\alpha, \beta$ を使って以下のように置きます。

$\displaystyle \frac{1}{(s+1)(s+2)} = \frac{\alpha}{s+1} + \frac{\beta}{s+2} \tag{1}$

この $\alpha, \beta$ を求めよ、というのが部分分数分解の問題です。

上の式を素朴に計算しようと思うなら、右辺を展開して連立方程式を解いたら良いわけですが、これがなかなか面倒です。

なかなか面倒な計算例：
式 $(1)$ の右辺を通分すると、

$\displaystyle \begin{align} \frac{\alpha}{s+1} + \frac{\beta}{s+2} &= \frac{\alpha(s+2) + \beta(s+1)}{(s+1)(s+2)} \\ &= \frac{(\alpha + \beta)s + (2\alpha + \beta)}{(s+1)(s+2)} \end{align}$

となります。左辺と係数比較すると

$\begin{cases} \alpha + \beta = 0 \\ 2\alpha + \beta = 1 \end{cases}$

なる連立方程式が得られます。これを解くと

$\begin{cases} \alpha = 1 \\ \beta = -1 \end{cases}$

となり、解が得られた。

これをエレガントに解く方法が冒頭のツイートだったのでした。

どのように計算するかというと

$\alpha$ を求めるためには、元の分数の $(s+1)$ を隠して、 $s = -1$ を代入する
$\beta$ を求めるためには、元の分数の $(s+2)$ を隠して、 $s = -2$ を代入する

たったこれだけです。簡単でしょう。

実際にやってみると

$\displaystyle \alpha = \left.\frac{1}{s+2}\right|_{s=-1} = 1$

$\displaystyle \beta = \left.\frac{1}{s+1}\right|_{s=-2} = -1$

となり、この $\alpha, \beta$ を $(1)$ 式に代入すると

$\displaystyle \frac{1}{(s+1)(s+2)} = \frac{1}{s+1} - \frac{1}{s+2}$

となって、あっという間に部分分数分解の答えが求まりました。すごいですね！

なぜこれでうまくいくのか

どうしてこんな方法でうまくいくのか考えてみましょう。

$\alpha$ の方で考えます。まず「元の分数の $(s+1)$ を隠して」の部分ですが、これは $(s+1)$ をかけることに相当します。そこで、式 $(1)$ の両辺に $(s+1)$ をかけてみましょう。

$\displaystyle \frac{1}{(s+2)} = \alpha + \frac{\beta}{s+2}(s+1)$

ここで、 $s = -1$ を代入すると

$\require{cancel} \displaystyle \left.\frac{1}{s+2}\right|_{s=-1} = \alpha + \cancel{\frac{\beta}{s+2}(s+1)}$

となり、 $\alpha$ だけが取り出せます。 $(s+1)$ をかけると $\alpha$ の分母が消え、一方で $\beta$ の分母がキャンセレーションしない、というのがポイントのようですね。 $\beta$ の計算も同様の方法で証明できます。

この方法を使えば、たとえばこんな複雑な部分分数分解も簡単に求まります。

$\displaystyle \frac{1}{(s+1)(s+2)(s+3)(s+4)(s+5)(s+6)(s+7)}$

暇な人はやってみてください。

どこまでうまくいくのか

ここで気になるのは、この方法の適用範囲ですね。たとえば、 $(s+1)$ の部分が $s^2 + s + 1$ のように次数が $2$ 以上の多項式の場合はどうでしょう。

$\displaystyle \frac{1}{(s^2 + s + 1)(s+2)}$

この場合は簡単で、複素数の範囲で因数分解してあげれば良いです。

$s^2 + s + 1 = (s - \gamma)(s - \delta)$

このようにすれば1次の多項式の積になりますから、同じ方法で部分分数分解が求まります。

あとは、分母の多項式が重解を持つときが気になります。

$\displaystyle \frac{1}{(s + 1)^2(s+2)}$

この場合も、少し手間がかかりますが、似たような方法（2階微分とかが入る）で計算が可能です。

この方向で一般化していくと、以下のブログに書かれた方法に行き着きます。この記事の「補題１」を御覧ください。
integers.hatenablog.com

INTEGERSというブログは、数学の面白いことならほぼ何でも書いてある素敵なブログです。

留数計算に似てる

この方法をみて私が思ったことは「留数計算に似てる」ということでした。実際、まったく等価な方法であることが以下のように示されます。

留数計算とは、複素関数論に出てくる定番の計算です。 $z = \alpha$ に極を持つ関数 $f(z)$ を考えて、 $z = \alpha$ の周りの経路 $C$ で複素積分することを考えます。

$\displaystyle \int_C f(z) dz$ （積分経路 $C$ は以下の図の通り）

f:id:tsujimotter:20180424222129p:plain:w320

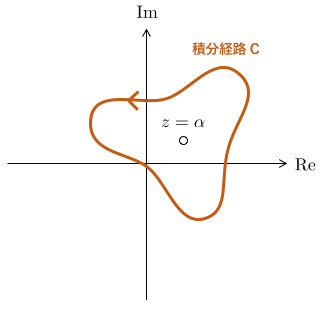
普通に計算しようとすると面倒ですが、実は留数を使って簡単に計算ができるというのが面白いところです。

テイラー展開に「負べきの項」を加えたものがローラン展開ですが、一般に任意の複素関数はローラン展開できます。 $f(z)$ が $z = \alpha$ で $1$ 位の極を持つと仮定して、 $z = \alpha$ の周りでローラン展開すると、以下のようになります：

$\displaystyle f(z) = \frac{a_{-1}}{(z - \alpha)} + a_0 + a_1 (z - \alpha) + a_2 (z - \alpha)^2 + a_3 (z - \alpha)^3 + \cdots \tag{2}$

$a_0$ 以降の部分がテイラー展開の部分（こういう部分を正則部分といいます）で、 $1/(z - \alpha)$ の項が本質的に極に関係する部分です。 $1/(z - \alpha)$ の項の係数 $a_{-1}$ を $f(z)$ の留数といいます。

先ほどの積分は、この留数を使って

$\displaystyle \int_C f(z) dz = 2\pi i a_{-1}$

と簡潔に表せます。

綺麗ですね。これが複素関数論の面白いところです。

この留数の求め方ですが、ローラン展開の式 $(2)$ に対して、 $(z - \alpha)$ をかけてあげると

$(z - \alpha)f(z) = a_{-1} + a_0(z - \alpha) + a_1 (z - \alpha)^2 + a_2 (z - \alpha)^3 + a_3 (z - \alpha)^4 + \cdots$

という具合に、一個ずつ項がずれます。これに $z - \alpha$ を代入すると、

$\begin{align} (z - \alpha)f(z)|_{z = \alpha} &= a_{-1} + \cancel{a_0(z - \alpha) + a_1 (z - \alpha)^2 + a_2 (z - \alpha)^3 + a_3 (z - \alpha)^4 + \cdots} \\ &= a_{-1} \end{align}$

となり、留数 $a_{-1}$ が取り出せました。

さて、ここで元々の部分分数分解を思い出して欲しいのですが、

これと

$\displaystyle \begin{align} \left.(s+1)\frac{1}{(s+1)(s+2)}\right|_{s=-1} &= \alpha + \cancel{\frac{\beta}{s+2}(s+1)} \\ & = \alpha \end{align}$

これ

$\displaystyle \begin{align} (z - \alpha)f(z)|_{z = \alpha} &= a_{-1} + \cancel{a_0(z - \alpha) + a_1 (z - \alpha)^2 + a_2 (z - \alpha)^3 + a_3 (z - \alpha)^4 + \cdots} \\ &= a_{-1} \end{align}$