この記事は 明日話したくなる数学豆知識アドベントカレンダー の 15 日目の記事です。( 14 日目:知られざる反例)
今日は、タイル張り(Tiling) という数学をご紹介します。
タイル張りとは、その名の通り、タイル状に隙間なく図形を並べること。以下にタイル張りの例を挙げます。タイル張りを使ったデザインは、日常の中でも、さまざまな場面で見かけるのではないでしょうか。


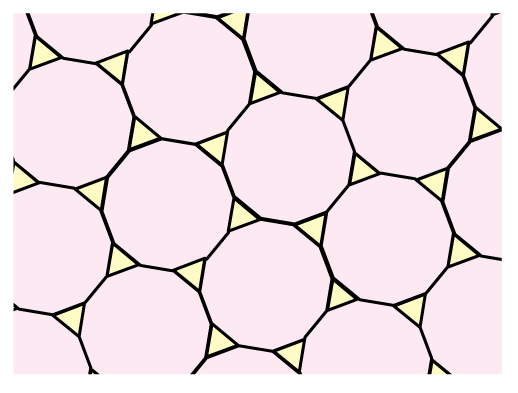
これらの例は正多角形によって構成されていますが、正多角形以外の図形であってもタイル張りは存在します。
本記事のタイトルにもなった 「ペンローズ・タイル」 も、正多角形でないタイル張りの仲間の1つです。ペンローズ・タイルは、一見シンプルに見えますが、非常に奇異な特徴をもっています。
まずは基本からご紹介しましょう。
ペンローズ・タイルは、「カイト」と「ダート」と呼ばれる、次の 2 つの図形によって構成されます。
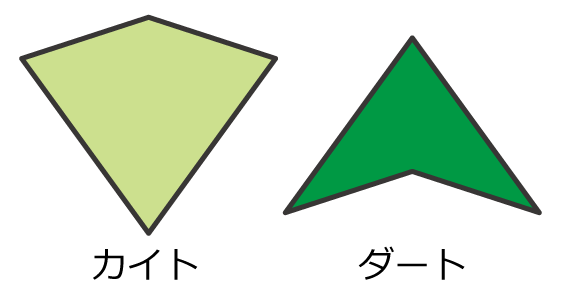
カイト(kite)は英語で凧の意味。お正月にあげる凧のような形をしていますね。
ダート(dart)は矢じりの意味です。ダートを複数形にすると「ダーツ」になります。名前のイメージからわかるように、先がとがった形をしていますね。
基本的な性質として、この2つを組み合わせると、次のような「ひし形」になります。
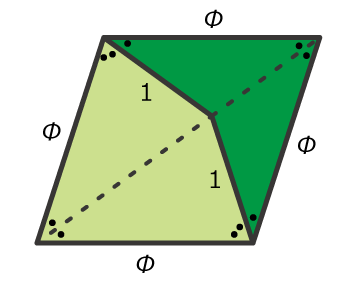
言い忘れていましたが、短いほうの辺の長さと長いほうの辺の長さの比が黄金比 になっています。
(読み方は「ファイ」ですよ)の定義は次の通りです。この値はよく知られていますね。
角度を考えると、小さいほうの角が (・が1つ)、大きいほうの角が
(・が2つ)となります。このあたりの角度は、正五角形の数学的性質に詳しい方には、おなじみではないでしょうか。
さて、上の図のように、カイトとダートの 2 つ 1 組でひし形を作れるので、次のような自明なタイル張りが存在します。

このタイル張りは周期的でわかりやすいですが、少々面白みに欠けますよね。ペンローズ・タイルのいったいどこが面白いのでしょう。
ペンローズ・タイルが他の一般的なタイル張りと異なる点は、非周期的 なタイル張りが存在することです。
実際に並べてみるのが一番わかりやすいでしょう。
見てください。
ドン!

どうです。すごいでしょう。
この図を作るのはなかなか苦労しました。笑
一見同じようなパターンのようで、よく見ると少しずつ違う。このような非周期的な並べ方は、画面からはみ出てた後もいつまでも続けることができます。
面白いですね。
ペンローズ・タイルを発見したのは、「ロジャー・ペンローズ」という今もご存命の理論物理学者です。彼はスティーブン・ホーキングと組んで、ブラックホールに関する重要な定理を導いたことで有名です。
が、しかし、物理のみならず、変わった図形をたくさん提案してその名を残しています。
「ペンローズの三角形」や「ペンローズの階段」などは、名前は聞いたことがなくても、一度は目にしたことがあるのでしょうか。
これらの図は、Wikipediaの「ロジャー・ペンローズ」の項目で見ることができます。
Wikipedia によると、彼はエッシャーのファンだったようですね。たしかに、あのエッシャーの絵のような、何やら神秘的な雰囲気をペンローズの作った図形は表現しているように思います。
最後に「ペンローズ・タイル」に興味を持ってくれたあなたのために、印刷用のPDFファイルを作ってみました。よかったら印刷して、切って貼って、試してみてください♪
それでは、今日はこの辺で。
明日話したくなる数学豆知識は明日も続きますよ。