単項化定理と群コホモロジー - tsujimotterのノートブック

こんにちは。最近、群コホモロジーがマイブームのtsujimotterです。

群コホモロジーといえば、以前の記事で群コホモロジーに関する定理「ヒルベルトの定理90」を使って、クンマー理論を導く話を書いたことがありました。
tsujimotter.hatenablog.com

今回はヒルベルトの定理94 という定理について紹介したいと思うのですが、実はこの証明にも群コホモロジーが登場し、クンマー理論のときとほとんど同じような流れで議論ができるのです。

なかなか面白いので、ぜひ最後までお付き合いください。

目次：

単項化定理

ヒルベルトの定理94

ヒルベルトの定理94の証明

おわりに

参考文献

単項化定理

まずは「単項化」とは何かについて説明するところから始めましょう。

代数体 $K$ の有限次ガロア拡大 $L/K$ を考え、 $K, L$ の整数環をそれぞれ $\newcommand{\OK}{\mathcal{O}_K}\newcommand{\OL}{\mathcal{O}_L}\OK, \; \OL$ とします。

$\OK$ の任意のイデアル $\newcommand{\a}{\mathfrak{a}}\a \subset \OK$ に対して、 $\a$ を $\OL$ のイデアルに「持ち上げ」ます。すなわち、 $\a\OL$ を考えるということですが、この $\a\OL$ を $\a$ の $L$ への延長といいます。

この $L$ への延長 $\a\OL$ が $\OL$ の単項イデアルになるとき、 $\a$ は $L$ において単項化するといいます。今回は、単項化の条件について考えたいと思います。

$\OK$ がもし単項イデアル整域であれば、任意のイデアル $\a \subset \mathcal{O}_K$ は単項イデアルです。そして、単項イデアル $\a$ の $L$ への延長 $\a\OL$ は $\OL$ の単項イデアルです。

ここで $\OK$ は単項イデアル整域とは限らないとします。この場合であっても、単項イデアルでない $\a$ が $\OL$ に延長したときに単項イデアルになることがあるのです。

たとえば、 $K = \mathbb{Q}(\sqrt{-5})$ とし、 $L = K(\sqrt{5})$ とします。このとき、 $\OK$ のイデアル $(2, \; 1+\sqrt{-5})$ はよく知られているように単項イデアルではありません。

参考：tsujimotter.hatenablog.com

しかしながら、 $L$ への延長 $(2, \; 1+\sqrt{-5})\OL$ を考えると、実はこれは $\OL$ の単項イデアルになるのです。すなわち、ある $\OL$ の元 $\alpha$ が存在して

$(2, \; 1+\sqrt{-5})\OL = \alpha\OL$

が成り立つということです。

このことはまったくもって自明ではありません。本当にそうなるのか直接確かめてみたいところですが、私自身確かめたわけではありません。計算してみたいと思いますが、実際問題としてなかなか大変だと思います。

しかしながら、次の単項化定理によって $(2, \; 1+\sqrt{-5})\OL$ が単項イデアルになることは保証できてしまうのです。

単項化定理（フルトヴェングラー , 1930）

$K$ を代数体とし，その整数環を $\OK$ とする． $\OK$ の任意のイデアル $\a$ は、 $K$ のヒルベルト類体 $L$ において単項化する．すなわち、 $\a$ の $L$ への延長 $\a\OL$ は単項イデアル．

$K = \mathbb{Q}(\sqrt{-5})$ のヒルベルト類体は $L = K(\sqrt{5})$ なので、単項化定理により上の例の $(2, \; 1+\sqrt{-5})\OL$ は単項イデアルとわかります。もっというと、 $(2, \; 1+\sqrt{-5})$ に限らず 任意の $\OK$ のイデアルは $L$ で単項化するというわけです。これはなかなかすごいですね。

ヒルベルトがヒルベルト類体を予想したときに、その特徴づけとして「すべてのイデアルが単項化すること」を挙げていたようです。単項化定理は、ヒルベルトによって予想され、その弟子のフィリップ・フルトヴェングラーによって証明されました。

単項化定理について、勘違いしやすいポイントが一つあるので注意をしておきます。

このブログで「ヒルベルト類体」が登場したのは初めてではありません。

参考：tsujimotter.hatenablog.com

このときに挙げたヒルベルト類体の重要な性質として次のようなものを紹介したかと思います。

$K$ を代数体， $L$ を $K$ のヒルベルト類体とする．このとき， $\OK$ の素イデアル $\newcommand{\p}{\mathfrak{p}}\p$ について，以下が成り立つ：

$\p$ が $\OK$ の単項イデアル $\; \Longleftrightarrow \;$ $\p$ は $\OL$ で完全分解 $\;\;\;\; \;\;\;\; (1)$

これを知っている人は、両者がごちゃ混ぜになって、こんがらがってくると思うのです（というか私がこんがらがっていました）。

両者の違いを述べると、次のように整理されます。

単項化定理： $K$ のイデアルを $L$ に延長すると、 $L$ のイデアルとして単項イデアルになる
上の必要十分条件 $(1)$ ： $K$ の素イデアルが単項イデアルである必要十分条件は、 $L$ に延長したときに完全分解することである

こうやって整理してみると、どちらも単項イデアルについて述べているものの、主張としては全然違うことを言っていると気づきますね。

単項化定理に関連して、類体塔問題という有名な問題にも触れておきたいと思います。

単項化定理によれば、 $K$ の整イデアルはすべて $K$ のヒルベルト類体 $K_1$ で単項化します。もし、 $K_1$ が単項イデアル整域でない場合は、 $K_2$ のヒルベルト類体に持ち上げれば $K_1$ の整イデアルは単項化します。もし、 $K_2$ が単項イデアル整域でない場合は、・・・のように $K_n$ が単項イデアル整域になるまで繰り返します。

このように $K$ のヒルベルト類体のそのまたヒルベルト類体を繰り返しとっていってできる体拡大の列

$K \subsetneq K_1 \subsetneq K_2 \subsetneq K_3 \subsetneq K_4 \subsetneq \cdots$

のことを 類体塔 といいます。

類体塔問題とは、任意の類体塔は有限回で止まるか？、すなわち、有限回で単項イデアル整域に到達するか？、という問題です。

類体塔問題は、1964年にシャファレビッチとゴロッドによって否定的に解かれました。すなわち、無限に続く類体塔が見つかったということです。実際、その反例は

$K = \mathbb{Q}(\sqrt{-2\cdot 3 \cdot 5\cdot 7\cdot 11\cdot 13\cdot 17})$

となっています。なかなか凄まじいですね。

実際に、この例が反例になっていることを確認するのはかなり大変です。私も理解していないのですが、群コホモロジーを使った議論が必要になるようです。いつかこのブログで解説できるようになりたいです。

ヒルベルトの定理94

話を単項化定理に戻しましょう。

単項化定理を予想したのは前述の通りヒルベルトですが、彼が予想するにあたって、その根拠とした定理があります。それがヒルベルトの定理94 です。

ヒルベルトの定理94（ヒルベルト, 1897）

$K$ を代数体とし， $L/K$ を $n$ 次不分岐巡回拡大とすると， $K$ の $n$ 個以上のイデアル類に属する任意のイデアルが $L$ において単項化する．

$K$ のイデアル類群 $\operatorname{Cl}(K)$ を考えて、そのイデアル類のうち $n$ 個に属するイデアルすべてが $L$ で単項化するという主張です。 $L/K$ としては「不分岐」かつ「巡回拡大」であるという限定した状況を仮定していて、単項化するイデアル類の個数 $n$ は、 $L/K$ の拡大次数というわけです。

この定理からヒルベルトが単項化定理を予想した流れは、次のものだと考えられます。

定理94から「巡回拡大」の条件を外して「アーベル拡大」とすることを考えましょう。すると、次のような主張になります。

$K$ を代数体とし， $L/K$ を $n$ 次不分岐アーベル拡大とすると， $K$ の $n$ 個以上のイデアル類に属する任意のイデアルが $L$ において単項化する．

ここでもし、上の主張が真であると仮定すると、 $L/K$ が最大不分岐アーベル拡大、すなわちヒルベルト類体としたとき、 $K$ の $[L : K]$ 個以上のイデアル類に属する任意のイデアルが $L$ において単項化することになります。ここでヒルベルト類体の性質

$\operatorname{Gal}(L/K) \simeq \operatorname{Cl}(K) \tag{2}$

を思い出すと、結局 $K$ の $\# \operatorname{Cl}(K)$ 個以上のイデアル類に属する任意のイデアルが $L$ において単項化することになります。つまり、 $K$ のイデアルすべてが単項化するというわけです。

このように考えると、確かに単項化定理は成り立ってほしいと思いたくなるわけですね。

ところで、ヒルベルトの構想によって単項化定理は証明されたのでしょうか？実は、巡回拡大の仮定を外したより一般的な命題は、1991年に鈴木浩志さんという方によって証明されているそうです。

しかしながら、歴史的な順番としては逆です。ヒルベルトが単項化定理を予想したのが1900年、フルトヴェングラーが証明したのは1930年であり、定理94の一般化はフルトヴェングラーの証明からずいぶん後です。また、フルトヴェングラーの証明は（私は理解できていませんが）どうも定理94の方向性ではないようです。

ヒルベルトの予想自体は当たっていたものの、証明の流れとしてはヒルベルトの構想通りには進まなかったということでしょうか。

参考：
彌永先生の数学的な業績 - 三宅克哉
https://mathsoc.jp/publication/tushin/1102/miyake11-2.pdf

さて、今日はヒルベルトの定理94の証明を紹介することにしましょう。

この定理の証明には群コホモロジーが使われます。これが実に鮮やかで面白いので、ぜひ紹介したいというわけです。

証明の最初のキーポイントは、単項化問題をうまいこと言い換えるということです。

$K, L$ の分数イデアル全体のなす群を $I_K, I_L$ 、単項分数イデアル全体のなす群をそれぞれ $P_K, P_L$ とします。

$L/K$ のガロア群を $G$ とおくと、 $G$ は $I_L, P_L$ に作用します。この作用で不変な部分集合を $I_L^G, P_L^G$ と記すことにしましょう。すなわち、

$I_L^G = \{ \a \in I_L \mid \forall \sigma \in G, \; \a^{\sigma} = \a \}$

$P_L^G = \{ \a \in P_L \mid \forall \sigma \in G, \; \a^{\sigma} = \a \}$

ということです。以降、 $G$ が上付き添え字で出てきたら、同じように考えます。

ここで、 $L/K$ を不分岐拡大とすると

$I_L^G$ は「 $K$ のイデアルを $L$ に延長したもの全体」
$P_L^G$ は「 $K$ のイデアルを $L$ に延長したもののうち、 $L$ で単項イデアルになるもの全体」

となります。

少し長くなりますが、上について説明をします。不分岐拡大という条件をつけた理由についても説明したいと思います。*1

まず具体例から考えたいのですが、 $K = \mathbb{Q}, \; L = \mathbb{Q}(\sqrt{-1})$ とします。この例では $L/K$ は不分岐拡大ではありませんが、あえてこのような例を考えています。

$(2) \subset \OK$ の $L$ における素イデアル分解を考えると

$(2)\OL = (1+\sqrt{-1})^2$

となり、これは分岐する素イデアルです。ここで、 $(1+\sqrt{-1})$ に $\sigma = (\sqrt{-1} \mapsto -\sqrt{-1}) \in G$ を作用させると

$(1+\sqrt{-1})^{\sigma} = (1-\sqrt{-1}) = (1+\sqrt{-1})$

となり、 $G$ 不変な $L$ のイデアルになります。したがって、 $(1+\sqrt{-1}) \in I_L^G$ です。

また、 $(1+\sqrt{-1})$ は明らかに $K$ のイデアルの $L$ への延長ではあり得ませんから

$I_L^G \neq \{ K$ のイデアルを $L$ に延長したもの $\}$

となってしまいます。

一方、 $(5) \subset \OK$ のような素イデアルとすると

$(5)\OL = (2+\sqrt{-1})(2-\sqrt{-1})$

となりこれは不分岐です。ここで

$(2+\sqrt{-1})^\sigma = (2-\sqrt{-1}) \neq (2+\sqrt{-1})$

$(2-\sqrt{-1})^\sigma = (2+\sqrt{-1}) \neq (2-\sqrt{-1})$

であり、 $(2+\sqrt{-1}), \; (2-\sqrt{-1})$ は $I_L$ の $G$ 不変な部分に含まれません。

以上の状況を図に表すと次のようになります。

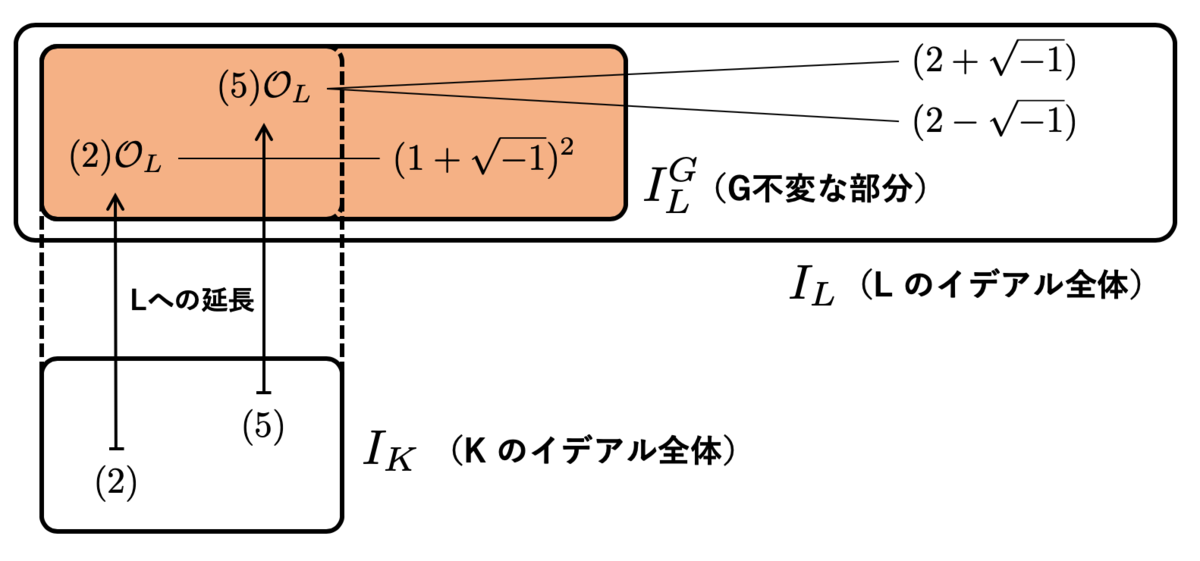
というわけで、分岐する素イデアルがなければ、 $I_L^G$ が $I_K$ の $L$ への延長とちょうど一致するのではないかということが示唆されます。

このことを踏まえて、一般的なガロア拡大 $L/K$ のケースで考えてみましょう。

$K$ の素イデアル $\mathfrak{p}$ の $L$ における素イデアル分解を考えます。

$\mathfrak{p}\OL = (\mathfrak{P}_1 \cdots \mathfrak{P}_g)^e$

両辺に $\sigma \in G$ を作用させると

$\mathfrak{p}\OL = (\mathfrak{p}\OL)^{\sigma} = (\mathfrak{P}_1^{\sigma} \cdots \mathfrak{P}_g^{\sigma})^e$

なので、

$\mathfrak{P}_1 \cdots \mathfrak{P}_g = \mathfrak{P}_1^{\sigma} \cdots \mathfrak{P}_g^{\sigma}$

が成り立ちます。

$G$ の元が集合 $\{ \mathfrak{P}_1, \ldots, \mathfrak{P}_g \}$ に推移的に作用することから、 $\mathfrak{P} = \mathfrak{P}_1$ とすると、 $\mathfrak{P}_i = \mathfrak{P}^\sigma$ なる $\sigma \in G$ が存在することがわかります。

よって

$g = 1 \; \Longleftrightarrow \;$ 任意の $\sigma \in G$ に対して $\mathfrak{P}^{\sigma} = \mathfrak{P} \; \Longleftrightarrow \; \mathfrak{P} \in I_L^G$

が言えます。

$g = 1$ のとき、以下の $(i), (ii)$ のケースが考えられます。

$(i)$ $e = 1$ ならば $\mathfrak{p}\OL = \mathfrak{P}$ であり、すなわち $\mathfrak{P}$ は $\mathfrak{P} \in I_L^G$ であり $\mathfrak{p}$ の $L$ への延長であるような素イデアル。

$(ii)$ $e > 1$ ならば $\mathfrak{p}\OL = \mathfrak{P}^e$ であり、すなわち $\mathfrak{P}$ は $\mathfrak{P} \in I_L^G$ であり $\mathfrak{p}$ の $L$ への延長ではないような素イデアル。

$L/K$ が不分岐拡大であれば、上の $(ii)$ のケースは存在しないので

$I_L^G = \{ K$ のイデアルを $L$ に延長したもの全体 $\}$

が成り立ちます。

また、 $P_L^G$ は $I_L^G$ のうち特に単項イデアルであるもの、すなわち単項化するもの全体になりますね。

よって、 $P_L^G/P_K$ を考えれば「 $L$ で単項化するイデアル類全体」を考えることになります。このイデアル類の個数が拡大次数 $n = [ L : K ]$ 以上であることが言えれば、ヒルベルトの定理94が証明できたことになります。

証明の最大のキーポイントは、上の $P_L^G/P_K$ を群コホモロジーによって表すという点です。

$P_L^G/P_K \simeq H^1(G, E_L)$

という同型がいえるので、右辺のコホモロジーの位数が $n$ 以上であることを示せばよいことになります。この部分に巡回拡大におけるコホモロジーの性質が使えます。面白いですね！

それでは、アウトラインはこの辺にしておいて、具体的な証明に行きましょう。

ヒルベルトの定理94の証明

（証明）
$P_K, \; P_L$ を $K, L$ の単項分数イデアルのなす群とし、 $E_L$ を $\OL$ の単数群とします。

$G = \operatorname{Gal}(L/K)$ として、次の $G$ 加群としての短完全列を考察します：

$1 \longrightarrow E_L \longrightarrow L^\times \longrightarrow P_L \longrightarrow 1 \tag{3}$

この完全列はイデアル類群の完全列

$1 \longrightarrow E_L \longrightarrow L^\times \longrightarrow I_L \longrightarrow \operatorname{Cl}(K) \longrightarrow 1$

に対して、 $I_L$ を $P_L$ に置き換えたものに対応しています。 $L^\times \longrightarrow I_L$ は全射とは限りませんが、 $L^\times \longrightarrow P_L$ は全射です。そのため、Cokerに相当する部分が 1 になって消えているというのが式 $(3)$ の完全列というわけですね。

短完全列 $(3)$ に対し、コホモロジー長完全列を作ると

$\begin{align} 1 &\longrightarrow H^0(G, E_L) \longrightarrow H^0(G, L^\times) \longrightarrow H^0(G, P_L) \\ &\longrightarrow H^1(G, E_L) \longrightarrow H^1(G, L^\times) \longrightarrow H^1(G, P_L) \longrightarrow \cdots \end{align}$

が得られます。

ヒルベルトの定理90

$H^1(G, L^\times) = 1$

と

$H^0(G, E_L) = E_L^G$

$H^0(G, L^\times) = (L^\times)^G$

$H^0(G, P_L) = P_L^G$

より

$1 \longrightarrow E_L^G \longrightarrow (L^\times)^G \longrightarrow P_L^G \longrightarrow H^1(G, E_L) \longrightarrow 1$

が得られます。

さらに、 $(L^\times)^G = K^\times$ より

$K^\times \xrightarrow{\;f\;} P_L^G \xrightarrow{\;g\;} H^1(G, E_L) \longrightarrow 1$

となります。完全性から、 $\operatorname{Ker}(g) = \operatorname{Im}(f) = P_K$ であり、 $g$ についての準同型定理 $P_L^G / \operatorname{Ker}(g) \simeq \operatorname{Im}(g) = H^1(G, E_L)$ と合わせて

$P_L^G/P_K \simeq H^1(G, E_L) \tag{4}$

が得られます。

前節で議論したように、 $L/K$ は不分岐拡大より、左辺の $P_L^G/P_K$ は「 $L$ で単項化するイデアル類全体」のなす群を表します。よって、右辺のコホモロジーの位数が $n = [L : K]$ 以上であることを示せばよいことになります。

ここでエルブラン商を定義します。 $H^0(G, E_L), \; H^1(G, E_L)$ の位数をそれぞれ $h^0(G, E_L), \; h^1(G, E_L)$ と表すことにして、その商

$h(G, E_L) := h^0(G, E_L) / h^1(G, E_L)$

を エルブラン商 といいます。

$E_L$ の構造を調べることによって、 $h(G, E_L)$ については以下の定理が成り立つことが示せます。

定理

$L/K$ を巡回拡大とし， $G$ を $L/K$ のガロア群とする． $E_L$ を $\OL$ の単数群とし， $\rho$ を $L/K$ で分岐する $K$ の無限素点の個数とすると，次が成り立つ：

$\displaystyle h(G, E_L) = \frac{2^\rho}{[L : K]} \tag{5}$

「類体論講義（参考文献）」の定理5.1.7に証明が載っていますが、難しいので今回は扱いません。

上の定理より、 $n$ 次不分岐巡回拡大 $L/K$ において

$h^1(G, E_L) = n \cdot h^0(G, E_L) \geq n$

が成り立ちます。

よって、 $(4)$ と合わせると

$\#(P_L^G/P_K) = h^1(G, E_L) \geq n$

が言えるので、 $K$ の $n$ 個以上のイデアル類に属する任意のイデアルが $L$ において単項化することが示せました。

（証明終わり）

おわりに

今回は、単項化定理に関する「ヒルベルトの定理94」の証明を紹介しました。

ヒルベルトの定理94とは、 $L/K$ が不分岐巡回拡大のとき $K$ のイデアル類のうち $n$ 個以上が単項化するという定理でした。その証明には群コホモロジーが使われました。「 $L$ で単項化するイデアル類」を表す群 $P_L^G/P_K$ を群コホモロジーで表すことによって、群コホモロジーの性質から位数を評価できる点が面白かったですね。

これまで群コホモロジーを使った議論についていくつか（クンマー理論や今回の話）勉強してきましたが、少なくともこれまで扱ってきた議論には、ある種の典型的なパターンのようなものがあると気づきました。