を代数体として
上定義された楕円曲線の
-有理点の群をモーデル・ヴェイユ群
といいます。モーデル・ヴェイユの定理によって、
が有限生成であることが示されていますが、その自由部分の生成元の個数、すなわちランクを決定するのは一筋縄ではありません。
今日は、セルマー群 という道具を使ってランクを計算するための 2-descent法 を私の理解できた範囲で紹介します。なかなか難しい内容なので、私の理解もまだ十分ではありません。誤りがあった際は、ご指摘頂けると嬉しいです。
モチベーション
本題のためのイントロとして、ランクの重要性について少し述べたいと思います。
前回の記事では「Knightの問題」が解を持つことの必要十分条件は「楕円曲線 のモーデル・ヴェイユ群
のランクが正」であることを示しました。
楕円曲線のランクが重要になる類似の問題として「合同数問題」があります。
が合同数である必要十分条件は、同様に楕円曲線
のモーデル・ヴェイユ群
のランクが正であることです。
tsujimotter.hatenablog.com
この記事を書く直接的なモチベーションになったのは、先週話題になった「周の長さと面積が等しい二等辺三角形と直角三角形のペア」についての研究です。
詳しいことはいずれ説明できたらいいなと思っていますが *1、簡単に言うと、目的の三角形の組全体の集合を「超楕円曲線の有理点」に対応させることができるのです。超楕円曲線は種数が2以上の代数曲線ですが、このヤコビ多様体というアーベル多様体を作ることができて、そのアーベル多様体のモーデル・ヴェイユ群に対して同じくランクを考えることができます。三角形のペアの一意性を示すために「Chabauty-Coleman 法」という手法を使うのですが、この手法が適用できる条件として「モーデル・ヴェイユ群のランクが1以下であること *2 」を示す必要があります。ランクが1以下であることを示すために、この論文では2-descent法が用いられています。
こんな風に整数論の問題を解くために、楕円曲線(やより一般のアーベル多様体)のモーデル・ヴェイユ群のランクがしばしば興味の対象になります。そこで、ランクを適切に評価したいというモチベーションが生まれます。
もちろんこの手の問題はそう簡単ではありません。ランクを求めるためには、無限位数の有理点の集合を求めて、それがモーデル・ヴェイユ群の自由パートを張ることを示さなければいけません。有限位数の集合は比較的簡単に求めることができるので、見つけた有理点が無限位数であるかどうかはわかります。それがすべての空間を張るかどうか調べるのが難しいというわけです。
楕円曲線 のモーデル・ヴェイユ群
のランクを評価するための有効な方法が、今日紹介したい
-descent法 *3 です。
–descent法とは、簡単に言えば
という群の「大きさ」を測る方法です。
がちょうどすっぽり収まるようなセルマー群という群を考えて、セルマー群の位数を評価することによって(間接的に)
の大きさを評価できるという方法です。
としては
を用いることができて、
の場合がよく用いられます。だから
-descent法というわけです。
ところで、本当に知りたいのは ではなくて、
だっただろうと思ったかもしれません。一般の加群
があって、
の大きさが分かったからといって、
の大きさが分かるわけではありません。ところが、楕円曲線のモーデル・ヴェイユ群の場合は、それが実行できます。ここでは詳細を述べませんが、「高さ関数(Height function)」と呼ばれる関数を適切に運用することで、2-descentによる
の大きさの評価から、
のランクを具体的に計算することができるのです。
Kummer系列とガロアコホモロジー
それでは本題に入るための準備をしていきましょう。
まずはセルマー群を定義するために、いくつか準備をしておきましょう。セルマー群は、ガロアコホモロジー という概念によって定義される群なので、以前の記事で紹介したようなガロアコホモロジーの取り扱いに慣れておく必要があります。
tsujimotter.hatenablog.com
ここでは少しだけ一般的な問題設定で考えます。「モチベーション」の節では、 上の楕円曲線だけを考察していましたが、ここではより一般に代数体
上定義された楕円曲線
を考えることにします。あとで必要になったときに、
とすればよいでしょう。
を
を含む体とし、
とします。
を
上定義された楕円曲線とし、
上の同種写像
が存在するとします。このとき、
は
に作用し、
–加群となります。
楕円曲線 間の同種写像が全射であることに注意する *4 と、
–加群としての次の完全列が得られます:
ここで、 と定義しています。上の完全列をKummer系列と呼びます *5 。
の類似物となっています。
Kummer系列に対して、上の記事と同様に( による)ガロアコホモロジーの長完全列をとりましょう *6。
ここで
であることから、完全列
を得ます。
さらに
と定義すると、右完全な完全列
が得られます。
これでひとまず事前準備完了です。
最後の完全列において
の写像は単射となっていますが、この写像をKummer mapといいます。このKummer mapによって、 という楕円曲線の
-有理点に関する群が、コホモロジー群の中に埋め込めるということが分かります。Kummer map を通して、楕円曲線の情報をコホモロジーの言葉で理解するというのが、ここで考えたいことなのです。
実際に を評価する際は、
という群そのものを考えるのではなく、セルマー群 と呼ばれる
の部分群を考えることになります。
セルマー群
この節では、いよいよセルマー群を定義しましょう。
完全列 の体
に2種類の体を代入して、新しい完全列を作ります。まず、
として完全列
を作りましょう:
次に (
は
の有限素点)として、同様に局所体
についての完全列を考えたあと、
のすべての有限素点
に対して直積をとって
を得ます:
Kummer mapによって、 を
の部分加群とみなすことで、
の完全列の3項目を2項目で割ると、
を得ます。
真ん中の写像は同型写像を与えています。
さて、完全列 を並べて以下の可換図式が得られます。
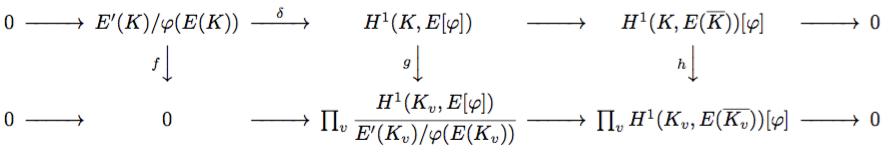
まず、 を並べて以下の可換図式を得ます:
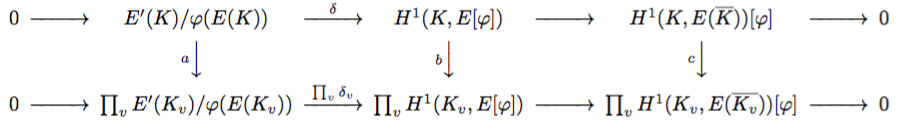
左の写像 は局所体
への埋め込み写像
によるものです。残りの2つの写像
は、付値
の
への延長を一つ固定したときに得られる埋め込み
によるガロア群の埋め込み
によって引き起こされる制限写像(を
に対して直積をとったもの)です。
さらに、この図式の下に を並べます。
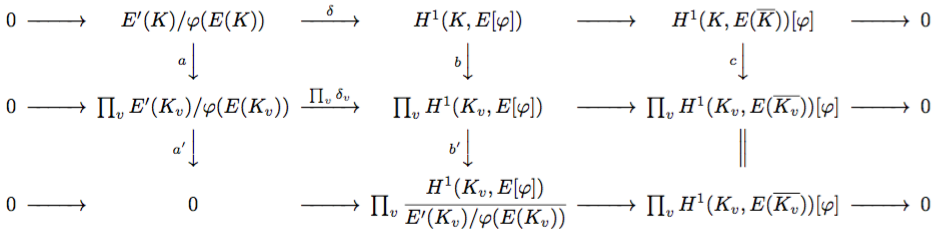
下の左右の四角が可換であることを示せば、 として目的の図式の可換性が示せます。
左側の図式について。 に対して、左回りの経路は
となる。右回りの経路は、
は単射より、
に埋め込まれた
の元は結局
に映されたときに 0 にいくため、結局
となる。よって、
が成り立ち図式が可換になる。
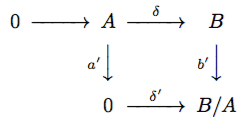
右側の図式について。完全性より は全射で、
は単射。自然な射影
に対して、準同型定理により図式を可換にする
が存在して(
)、
が同型写像となります。
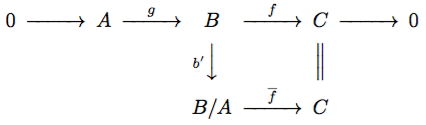
得られた可換図式に対して、蛇の補題を適用すると
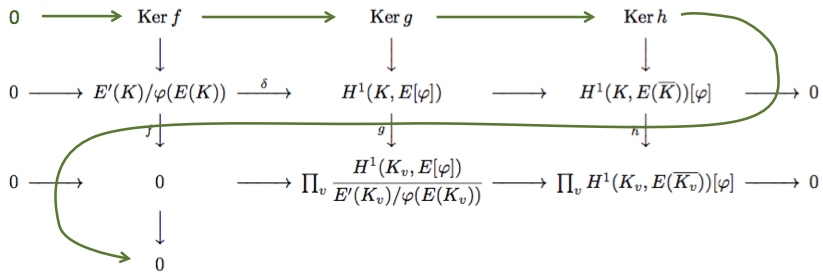
となって、新しい完全列
を得ます *7 。
ここで、 は
です。
このとき、2つの重要な群を定義しましょう。長かったですが、ようやくセルマー群の登場です。
実際、このように定義すると、あきらかに ,
となります。したがって、完全列
より
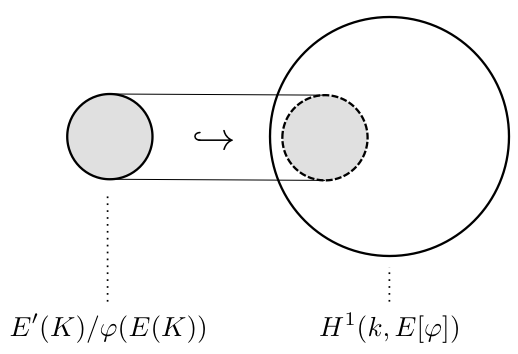
が得られます。この完全列こそが、今回の記事で得たかった最も重要な結論です。
セルマー群の重要性はこの完全列にあると思います。完全列の意味するところを説明するために、イメージ図を以下に示します。
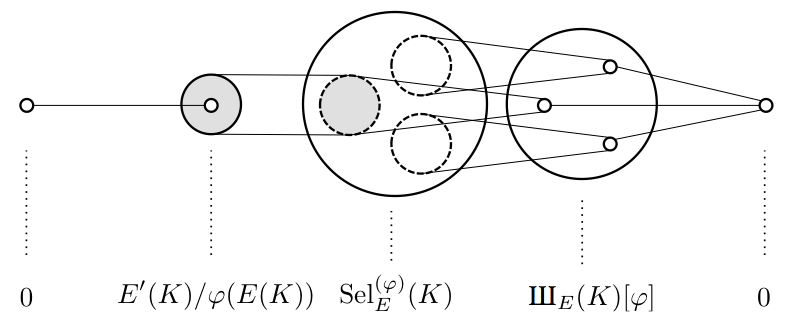
完全性から、 は単射となります。つまり、
の構造をそのままにセルマー群
に埋め込むことができるということですね。したがって、セルマー群の世界の中で
を理解することができるということです。
一方で、 は
そのものではありません。同型ではないので、そこに「ずれ」が生じます。
の世界がどの程度
からずれているのかを表す群がテイト・シャファレビッチ群
だというわけです。
代数体 の乗法群とその分数イデアル全体の群
に対して、次のような完全列を作ることができます:
ここで、核にあたる部分が単数群 で、余核にあたる部分がイデアル類群
です。イデアル類群
は、数の世界
をイデアルの世界
に写したときの「ずれ」を表す群になっています。
セルマー群とテイト・シャファレビッチ群という2つの群を紹介しましたが、それらの意味合いは一体何なのでしょうか?
これらは「局所大域原理」に関係しているようなのですが、まだ私は説明できるようなレベルに至っていません。ぜひ知りたいと思っていますので、そのうち理解できたら紹介したいと思います。
 –descent
–descent
ここで、 を
倍写像とし
としましょう。このセッティングでは、
は
の自己準同型を考えていることになります。
これらを代入すると、完全列 より
を得ます。
我々が知りたいのは の大きさですが、これを直接計算するのは困難です。そのため
を直接計算するのは諦めて、上の完全列を使って間接的に計算します。
[1] によると、完全列の真ん中にあるセルマー群 は有限群であることがわかっており、セルマー群を実際に計算することも可能です*9。また、完全性より
は単射です。この単射によって、
を用いて大きさを上から評価することができるのです。これを
–descent といいます。冒頭で述べたように、実用上は
–descent が用いられるようです。
さらに、テイト・シャファレビッチ群の大きさ がわかれば、
の大きさが決定できます。たとえば、
であれば
が言えてしまうわけです。しかしながら、この を計算するのは、たとえ
に限定したとしても、とても困難なことなのだそうです。
テイト・シャファレビッチ群については、理論的にもよくわかっていません。たとえば、こんなことでさえもまだ未解決です。
一応注意しておくと、有限群かわかっていないのは の方です。
については、セルマー群が有限群なので完全性から自動的に有限群となります。
まとめ
のランクを決定するために、
の大きさをどのように評価するか、というのが本記事の主題でした。
の直接的な計算は非常に難しい問題です。一方で、ガロアコホモロジーを使った議論によって、
は Kummer map によってコホモロジー
の中に埋め込めることがわかりました。
さらに、 の部分群には、セルマー群と呼ばれる重要な群
がある。セルマー群には以下の完全列があります。
セルマー群 は有限群であることが知られ、計算も実行可能なのだそうです。完全列を通してセルマー群を介して、
の大きさを議論することができます。これが2-descent法なのでした。
セルマー群は今回のテーマに限らずとても重要な対象です。tsujimotterのノートブックでも今後も登場するのではないかと思います。
それでは、今日はこの辺で。
参考
[1] 横山俊一「計算する立場からの楕円曲線論入門」,山形大学理学部数理科学科2014 年度後期「数理情報特選F/数理科学特別講義E」講義資料1
http://www.comp.tmu.ac.jp/s-yokoyama/lectures/2015-2018/files/2014Yamagata.pdf
[2] 後藤丈志「古典的 Diophantus 問題に対応する楕円曲線のセルマー群と有向グラフ」,2006年度整数論サマースクール報告集
http://www.ma.noda.tus.ac.jp/u/ha/SS2006/Data/Hokoku/goto.pdf
[3] 永田雄一「楕円曲線のsecond [2]-descent の計算について」
https://www.math.kyoto-u.ac.jp/~yukie/nagata-shuron.pdf
*1:勉強しようと論文はダウンロードしてみました!
*2:Chabauty-Coleman 法が適用できる正確な条件は「超楕円曲線のヤコビ多様体の有理点のランクが、超楕円曲線の種数(つまりヤコビ多様体の次元)より小さい」です。この問題の場合は種数が2なので、ランクが1であることを示す必要があります。
*3:日本語だと -降下法
*4:つまり が消える
*5:細かい注意ですが、過去の記事では「クンマー完全系列」と呼んでいました。同じものです。
*6:前回は群コホモロジーの表記に合わせて のように書いていました。一方で、
を
の絶対ガロア群としたときの、ガロアコホモロジーは一般に
と表記されることが多いため、今回はこのように表記します。
*7:2本の完全列のうち、上の系列の左端が 0 になっていることに注意しましょう。つまり が単射。このとき、蛇の補題で得られる系列の左端の射
が単射になることが示せます。したがって、得られる系列は 0 から始まる完全列になります。
*8:Шの記号はキリル文字の「シャー」です。シャファレビッチのスペリングがШから始まるためです。Шは通常のLaTeXではでないので、私は無理やりユニコードの文字を入れています。もしかすると、環境によっては見えないかも・・・。
*9:といいつつ、私自身は の定義が複雑でよく理解できていないため、具体的な計算の方法は知りません。。。