tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

類体論のステートメント

数学 類体論 整数論

今日は 類体論 のステートメント（主張）を述べて、その簡単な解説をしたいと思います。

類体論のステートメントは、大きく２種類あって、

  • 合同イデアル群を用いたもの
  • イデール群を用いたもの

があります。また、今回は単に「類体論」と言っていますが、

  • 大域類体論
  • 局所類体論

の２種類があります。代数体に対する類体論が大域類体論で、局所体に対する類体論が局所類体論です。

今日は、合同イデアル群 を用いた 大域類体論 のお話をします。つまり、代数体についての理論です。

イデール群を使った類体論の定式化については、id:unaoya さんが次の記事でまとめてくれています：
unaoya-pi.hatenablog.com


これまでも本ブログで「類体論的現象」についてはいくつか紹介してきましたが、類体論そのものについてまとめたことはありませんでした。本当はずっと以前からまとめたいと考えていたのですが、「無限素点」の取り扱いに自信がなかったためお蔵入りとなっていたのでした。ようやく出してもいいかもしれないと思えるようになったので、出してみたいと思います（間違ったことを言っていたらごめんなさい）。

無限素点に関してはやはり扱いが面倒だと感じたので、前半では無限素点を考える必要のない 「総虚な体」 上に限定した話をします。ただし、今後のことも考えて、後半でおまけ程度に一般の場合の話もします。


ちなみに今回の記事は、今後書きたい記事の前提知識を与えることを目的として書いています。そのため、内容としては最低限のものしか述べないつもりです。ご了承ください。

目次：

前提知識：素イデアル分解とフロベニウス

この節では、本記事で必要となる前提知識について駆け足で振り返りたいと思います。この節の内容については別の記事でも詳しく書いたので、この節の内容を読んでもよくわからなかったという人は、リンク先の記事を適宜参考にしてください。
tsujimotter.hatenablog.com


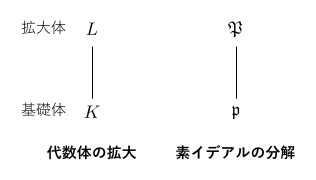
総虚な 代数体を K とし、 K 上の有限次アーベル拡大を L/K とします。類体論は、この L/K についての素イデアル分解を、 L/K のガロア群 \newcommand{\gal}{\text{Gal}} \gal(L/K) を通して理解するための理論といっていいかもしれません。

本当は、類体論は一般のガロア群に対して定式化した上で、後から「（これらの法則は）ガロア群がアーベルの場合にかぎられる」とするのですが、それをやってしまうと随分と煩雑になるので、今回はアーベル拡大に限定して定式化します。

K の整数環を \newcommand{\ok}{\mathcal{O}_{K}} \newcommand{\ol}{\mathcal{O}_{L}} \ok とし、対応する素イデアルを \newcommand{\pee}{\mathfrak{p}} \newcommand{\Pee}{\mathfrak{P}} \pee と表すことにします。以下、「 K の整数環 \ok の素イデアル \pee」というのは面倒なので、簡単に「 K の素イデアル \pee」と呼ぶことにしたいと思います。これは整数論で一般的に用いられる呼び方です。

さて、 K の素イデアル \pee を固定し、これを L に持ち上げることを考えましょう。すなわち、 \pee \ol を考えます。 \ol はもちろん L の整数環です。このとき、よく知られたように \pee \ol は、 \ol において素イデアルとは限らず、一般に L の素イデアルの積に分解されます。

この分解の様子は、 L/K がガロア拡大であれば一般に

\pee \ol = (\Pee_1 \Pee_2 \cdots \Pee_g)^{e} \tag{1}

と表すことができます。

式 (1) において、指数 e が e \geq 2 であれば「 \pee は L/K で分岐する」、そうでないときは「 \pee は L/K で不分岐である」といいます。また不分岐かつ g = [L : K] であれば「 \pee は L/K で完全分解する」といいます。

以下では、 \pee \ol を割り切る L の素イデアルの１つを固定し \Pee と表しましょう。 \Pee が \pee を割り切ることを、 \Pee \mid \pee と表すことにしましょう。

つまり、次のような状況を考えていることになります。

f:id:tsujimotter:20180513164156p:plain:w280
以前の記事でも注意したことですが、この分野では素イデアルの表記にドイツ文字の筆記体である「フラクトゥーア」が用いられます。 \pee は小文字の「ペー」を表し、 \Pee は大文字の「ペー」を表します。この記事でも習慣に則り、これらの記号を用いることにします。書きにくければ、単に p, P を使ってもいいように思います。

このほかに、以下の記号が現れます。どの記号も「イデアル」を表すのに用います。

  • \newcommand{\c}{\mathfrak{c}} \c : c のフラクトゥーア
  • \newcommand{\a}{\mathfrak{a}} \a : a のフラクトゥーア


さて、今後の議論における重要な道具として フロベニウス を定義します。 \ok / \pee, \; \ol / \Pee はそれぞれ有限体となり、後者は前者の有限次拡大となっています。有限体の拡大は素性がよく知られていて、そのガロア群 \widetilde{G} := \gal(\ok / \pee \big/ \ol / \Pee) は非常にわかりやすい形をしています。

\widetilde{\sigma_{\pee}} : x \mapsto x^{N_{K/\mathbb{Q}} \pee}, \;\; x \in \ol/\Pee \tag{2}

という写像を考えると、これは \ok / \pee の元を固定する \ol / \Pee の自己同型となっています。さらに、 \widetilde{G} は \widetilde{\sigma_{\pee}} を生成元とする巡回群となっています。

一方、 G に対して、 \Pee に対応した部分群 Z_{\Pee} \subset G を以下のように定義します：

Z_{\Pee} := \{ \sigma \in G \mid \Pee^{\sigma} = \Pee \} \tag{3}

これを \Pee の分解群と呼びます。 \Pee の分解群から、有限体のガロア群への自然な写像 Z_{\Pee} \to \widetilde{G} は全射になることが知られています。この写像の核を \Pee の惰性群といって I_{\Pee} と表します。

ここでもし、惰性群 I_{\Pee} が潰れている場合、\pee が不分岐となります。このとき、 Z_{\Pee} \to \widetilde{G} は同型写像となり、式 (2) の写像 \widetilde{\sigma_{\pee}} の Z \subset G への持ち上げが存在します。 L/K がアーベル拡大の場合は、この持ち上げは \Pee \mid \pee によらず、 \pee に対して一意に定まります。したがって、これを \pee のフロベニウスと呼んで、 \sigma_{\pee} と表すことにします。

この \pee のフロベニウス \sigma_\pee が非常に重要で、アーベル拡大 L/K で \pee が完全分解する条件を定めてくれます。具体的には、 \pee が不分岐のとき \sigma_{\pee} が定まり

\sigma_{\pee} = 1 \;\; \Longleftrightarrow \;\; \pee は L/K で完全分解

となります。


アルティン写像

上で述べたように、 \pee のフロベニウス \sigma_{\pee} は、 K の素イデアル \pee に対応する G = \gal(L/K) の元を指していました。この対応関係は

K の素イデアル と ガロア群 G の対応関係

を表しているように見えます。これを拡張して「 K の分数イデアル」と「ガロア群」の対応関係を定める写像を考えましょう。

ただし、分岐する素イデアルはうまく避ける必要があります。 L/K の分岐するすべての素イデアルをすべて含む K の素イデアルの有限集合 S = \{ \pee_1, \pee_2, \cdots, \pee_k \} を考えます。

L/K で分岐する素イデアルはすべて S に入っている必要がありますが、 S に L/K で分岐しない素イデアルが入っていてもかまいません。また、今回の設定では、分岐する素イデアルは有限個しか存在しないので、有限集合を考えれば十分です。

S をすべて掛け合わせてできる整イデアルを \c としましょう。すなわち

\displaystyle \c := \prod_{\pee \in S} \pee

です。

ここで、 \c と素な K の分数イデアル \a を考えます。「 \c と素」の意味は、 \c の素イデアルによって、割り切れないという意味です。 \a を素イデアル分解したときに現れる素イデアルは、すべて L/K では分岐しません。このような分数イデアル全体を I_K(\c) と定義します。つまり、こういうことです。

I_K(\c) := \{ \c と素な K の分数イデアル \}

分数イデアル \a \in I_K(\c) の素イデアル分解を

\displaystyle \a = \prod_{\pee \mid \a} \pee^{e_\pee}

と表したとき、以下の写像

\displaystyle (\cdot, L/K) : \a \mapsto \prod_{\pee \mid \a} \sigma_\pee^{e_\pee} \tag{4}

を考えます。これは、要するに \a を割り切るすべての素イデアルを、対応するフロベニウスに置き換えて（機械的に）掛け合わせたものとなっています。この写像の行き先は G = \gal(L/K) の元になっており、写像

\displaystyle (\cdot, L/K) : I_K(\c) \longrightarrow \gal(L/K) \tag{5}

が得られたことになります。これを アルティン写像 と呼ぶことにします。

左辺の I_K(\c) はアーベル群となっており、アルティン写像は、群準同型写像となっています。このアルティン写像の性質が、類体論においては重要になります。

導手とray類体

アルティン写像の持つ重要な性質は、アルティン相互法則です。（弱い版の）アルティン相互法則は、 L で分岐するような K の素イデアルで割り切れる整イデアル \c \subset \mathcal{O}_K で、任意の \alpha \in K^\times に対して

\alpha \equiv 1 \pmod{\c}\;\; \Longrightarrow \;\; ( (\alpha), L/K) = 1

を満たすものが存在する、という法則です。

この法則を考えるときには、 \alpha \equiv 1 \pmod{\c} であるような K の単項分数イデアル (\alpha) 全体を集めた集合を考えると便利でしょう。これを P_K(\c) とします。

P_K(\c) := \{ (\alpha) \mid \alpha \in K^\times, \; \alpha \equiv 1 \pmod{\c} \}

P_K(\c) はアーベル群となり、 I_K(\c) の部分群となります。

ここで、一点注意をしておきます。 P_K(\c) の定義は、 \alpha \equiv 1 \pmod{\c} なる単項分数イデアル (\alpha) 全体です。

一方で、 \alpha \not\equiv 1 \pmod{\c} であっても、 (\alpha) \in P_K(\c) であるかもしれません。というのも、 (\alpha) = (-\alpha) なので、もし -\alpha が -\alpha \equiv 1 \pmod{\c} を満たせば、 (\alpha) は P_K(\c) の元となるからです。

K の単数は -1 だけとは限りません。 \xi \in \mathcal{O}_K^{\times} として、 \xi \alpha \equiv 1 \pmod{\c} となるような \xi が存在すれば、 (\alpha) \in P_K(\c) となります。

すると、アルティン相互法則は次のように言い換えられます。こっちを覚えましょう。

（弱い版の）アルティン相互法則
L/K を代数体の有限次アーベル拡大とする． L で分岐するような K の素イデアルで割り切れる整イデアル \c \subset \mathcal{O}_K で
\a \in P_K(\c) \;\; \Longrightarrow \;\; (\a, L/K) = 1 \tag{6}

が成り立つものが存在する．

上の法則は、適切な \c をとれば、 (\a, L/K) = 1 となる \a は（つまり、アルティン写像の核は） P_K(\c) を含むということを表しています。

f:id:tsujimotter:20180513170757p:plain:w360

もちろん、このような \c は一つとは限りません。もし \c_1, \c_2 について上の法則が成り立つならば、 \c_1 + \c_2 についても成り立ちます。ここで、 \c_1 + \c_2 の方が大きなイデアルになっています。

そこで、このような法則が成り立つような、最大の整イデアルを考えたくなります。すなわち、上の法則が成り立つ整イデアルの最大公約イデアルです。このような性質を持つイデアルを L/K の 導手 とよび、 \c_{L/K} で表します。


導手はとても重要な量で、たとえば L/K, \; L'/K という二つの拡大を考え、それぞれの導手を \c_{L/K}, \c_{L'/K} としたときに、以下が成り立ちます：

\c_{L/K} \mid \c_{L'/K} \;\; \Longrightarrow \;\; L \subset L' \tag{7}

導手を割り切るかどうかと、拡大体が包含されるかどうかが対応しているわけですね。

このように導手を定義すると、ある整イデアル \c に対して、その \c を割り切る導手を持つ最大の体を考えたくなります。これを \c の ray類体 と呼びます *1。

定義（ray類体）
\c を K の整イデアルとする． K の \c を法とするray類体とは，有限次アーベル拡大 K_{\c}/K であって，任意の有限次アーベル拡大 L/K に対し
\c_{L/K} \mid \c \;\; \Longrightarrow \;\; L \subset K_{\c} \tag{8}

という性質をもつものである．また，このようなray類体 K_\c は， \c に対して一意に存在する．

ray類体は、与えられた \c を割り切る導手を持つ「最大」の体、と考えていいでしょう。ただし、 K_{\c} の導手が、必ずしも \c に一致する必要はありません。

類体論の主定理

以上の準備を元に、類体論の主定理を述べることができます。

類体論の主定理
L/K を代数体の有限次アーベル拡大とする．このとき，アルティン写像
(\cdot, L/K) : I(\c_{L/K}) \longrightarrow \gal(L/K) \tag{9}

は全射準同型であり，アルティン写像の核は (N_{L/K} I_L) P(\c_{L/K}) である．ここで I_L は L の 0 でない分数イデアルのなす群である．

さて、上の定理を見てぱっと意味がわからないかもしれません。私もそうでした。ここでは、かなり多くの情報が上の数行に含まれているということを指摘しておきたいと思います。

まず、すぐにわかることは、主定理によって L/K のガロア群の同型が具体的に与えられるということです。

アルティン写像の全射性より \text{Im}\, (\cdot{}, L/K) = \gal(L/K) がいえます。また、上の定理よりアルティン写像の核は \text{Ker}\, (\cdot{}, L/K) = (N_{L/K} I_L) P(\c_{L/K}) であるから、準同型定理 I(\c_{L/K}) \big/ \text{Ker}\, (\cdot{}, L/K) \simeq \text{Im}\, (\cdot{}, L/K) より

I(\c_{L/K}) \big/ (N_{L/K} I_L) P(\c_{L/K}) \simeq \gal(L/K) \tag{10}

が得られます。右辺は、 L/K のガロア群ですから、 L/K のガロア群の同型写像が得られたことになります。

また、左辺は K の分数イデアル I(\c_{L/K}) をその部分群 H := (N_{L/K} I_L) P(\c_{L/K}) で割ったものになっており、したがって K の分数イデアルの剰余類となっています。つまり、 K は基礎体の分数イデアルのある類別によってガロア群が表現されている、と考えることができます。

H は P_K(\c_{L/K}) を含む I_K(\c_{L/K}) の部分群となっています。このような H を合同イデアル群といい、また合同イデアル群に対応する K の拡大体 L/K のことを類体といいます。

f:id:tsujimotter:20180513164231p:plain:w600
上の法則は「 K 上の任意のアーベル拡大は類体である」ということを主張しています。これこそが「類体論」の名前の由来です。


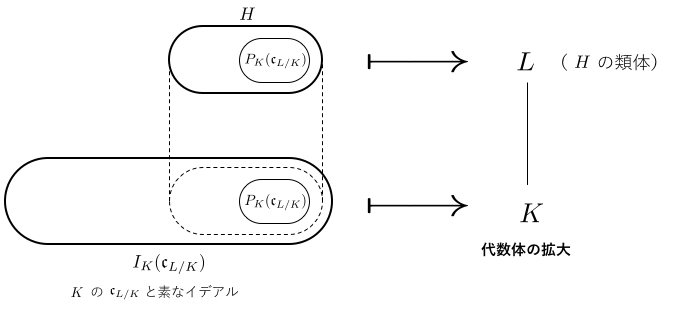
「ガロア群の同型がわかったところで何になるのだ？」と思ったかもしれません。しかし、この同型写像の情報こそが重要で、ここからただちに素イデアル分解法則が導かれます。

まず、この同型がアルティン写像によって構成されていることに注意しましょう。 K の素イデアル \pee が L/K で不分岐のとき、 \pee が完全分解する必要十分条件は、 (\pee, L/K) = 1 であることです。すなわち、 \pee \in I_K(\c_{L/K}) がアルティン写像 (\cdot, L/K) の核に含まれることです。ということは、上の主定理より

\pee \in (N_{L/K} I_L) P(\c_{L/K})

であれば、 \pee は L/K で完全分解することになります。アルティン写像の核 (N_{L/K} I_L) P(\c_{L/K}) は P(\c_{L/K}) より大きいことに再度注意しましょう。


さて、この核をより小さくしていき、完全分解する素イデアルの数を減らしてみましょう。すると、上の主定理より、相対的にガロア群が大きくなります。ガロア群が大きくなるということは、拡大としては大きくなるわけですね。一方で、 \c を割り切る導手を持つ拡大においては、アルティン写像の核は常に P_K(\c) を含みます（アルティン相互法則より）。

f:id:tsujimotter:20180513184106p:plain:w360

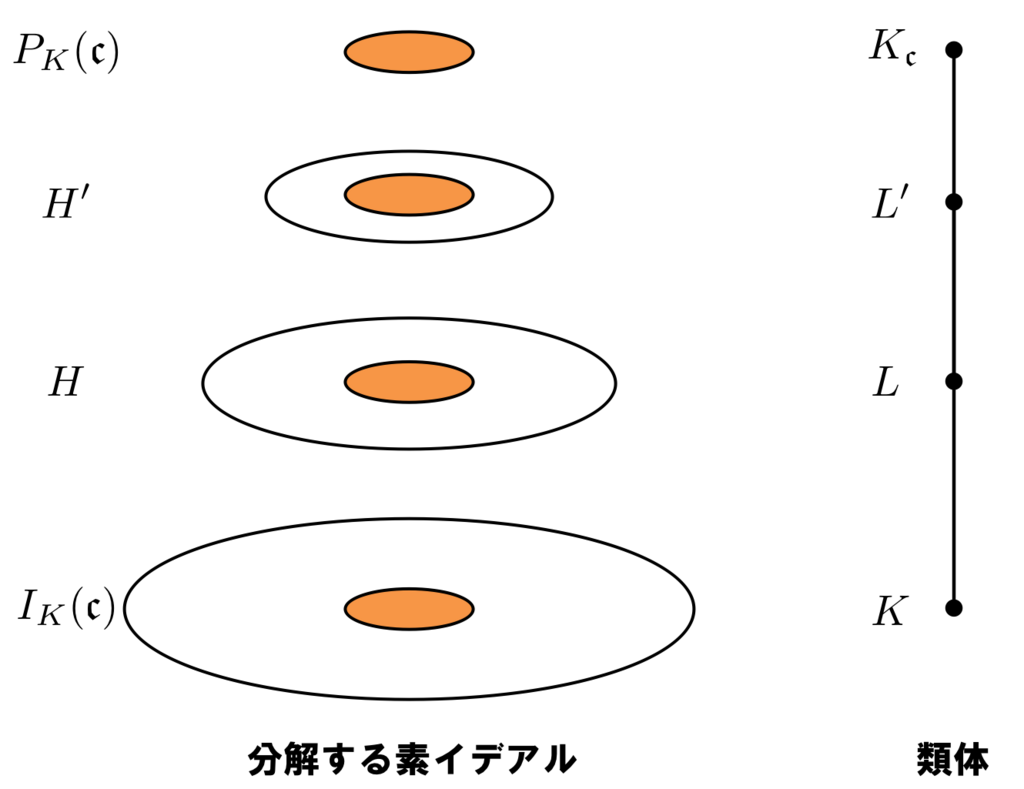
「同じ整イデアルを割り切る導手を持つ拡大の中で最大のもの」はまさにray類体の定義ですが、実は \c のray類体 K_\c では、ちょうど P_K(\c) に含まれる素イデアルだけがアルティン写像の核に含まれます。

定理（ray類体の特徴付け）
K を代数体とし， \c を K の整イデアルとする．このとき， K のray類体 K_\c は K のアーベル拡大であり
\{ K_{\c}/K で完全分解する K の素イデアル \} \;\; = \;\; \{ P_K(\c) に属する素イデアル \}

なる性質で特徴付けられる．

つまり、一般のアーベル拡大 L/K においては

\pee \in P_K(\c_{L/K}) \;\; \Longrightarrow \;\; (\pee, L/K) = 1

が成り立つのに対し、ray類体ではさらに逆も成り立ち

\pee \in P_K(\c) \;\; \Longleftrightarrow \;\; (\pee, K_{\c}/K) = 1 \tag{11}

という性質で特徴付けられるということです。

この性質はしばしば用いられるので覚えておくとよいでしょう。たとえば、ray類体を具体的に決定するときには、完全分解される素イデアルの集合を考えることになります（記事最後の円分体の例を参照）。


駆け足でしたが、類体論の主定理の説明は以上です。以下では、具体的なray類体について計算してみましょう。

具体例：ヒルベルト類体

\c = (1) とした場合を考えましょう。このとき、 \c を導手に持つ拡大 L/K においては、分岐する素イデアルは存在しません。したがって、不分岐拡大となります。 \c を法とするray類体は、そのような拡大の中で最大のものとなりますので、最大不分岐アーベル拡大となります。このような拡大を K のヒルベルト類体と呼びます。

K のヒルベルト類体を H/K としたときに、このガロア群は具体的に表されるでしょうか。アルティン写像の核は P_K( (1) ) を含むので、このような拡大の中で最大のものは核が P_K( (1) ) に一致する類体となります。したがって、類体論の主定理より

I_K( (1) ) \big/ P_K( (1) ) \simeq \gal(H/K)

となります。

ここで

I_K( (1) ) = \{ K の 0 でない分数イデアル \} = I_K
P_K( (1) ) = \{ K の 0 でない単項分数イデアル \} = P_K

となり、 \text{Cl}_K := I_K / P_K は K のイデアル類群となりますから、以下が得られます：

ヒルベルト類体の同型定理
H/K を K のヒルベルト類体とする．このとき，以下の同型が得られる：
\text{Cl}_K \simeq \gal(H/K) \tag{12}

ここで， \text{Cl}_K は K のイデアル類群．

私、この法則好きなんですよね。イデアル類群と最大不分岐アーベル拡大という性質が綺麗に結びつく。これこそが美しい法則だと思うのです。


さらに、アルティン写像から

\pee \in P_K \;\; \Longleftrightarrow \;\; (\pee, H/K) = 1

が言えるので、次の分解法則も得られます：

ヒルベルト類体の素イデアル分解法則
H/K を K のヒルベルト類体とする．このとき， K の任意の素イデアル \pee に対して，以下の分解法則がある．
\pee \in P_K \;\; \Longleftrightarrow \;\; \pee は H/K で完全分解

またいずれ、具体的にヒルベルト類体を決定するために、これらの法則に戻ってきたいと思います。

さて、ヒルベルト類体の例としては、たとえば K = \mathbb{Q}(\sqrt{-5}) 上のヒルベルト類体 H = K(\sqrt{-1}) があります。 H/K において分解する素イデアルは素数 p \equiv 1, 9 \pmod{20} の上にあるものに限られます。この場合、素イデアル分解法則からヒルベルト類体がわかるというよりは、ヒルベルト類体を特定しておいてその分解法則から素イデアルが単項イデアルであることが判明するといった使い方をします。以上の考え方のもと、たとえば2次形式でかける素数の法則が得られます。
tsujimotter.hatenablog.com

また、 \mathbb{Q} 上の不分岐な拡大は \mathbb{Q} 以外にはありません。このことは \mathbb{Q} の類数が 1 であることからもわかります。

無限素点を考慮した修正

さて、以上で終わりにしてもよかったのですが、やはり「総虚な」という条件がついた状態では納得いかないでしょう。おまけに、まだ円分体の例を計算していません。円分体の議論をするためには、無限素点における議論がどうしても必要です。以下では，総虚とは限らない体 K について、 K の上の類体論がどのように修正されるか考えましょう。

このことを説明するためには、そもそも「有限素点」と「無限素点」というものがあるという話をしなければなりません。必要最低限の説明をします。

まず、付値という写像 v : K \to \mathbb{R} を考えます。これは単なる写像ではなく、乗法性や三角不等式等の条件が付いた写像です。付値は、いわゆる「距離」のようなものを表していて、たとえば a, b \in K に対して v(a - b) が十分に小さければ a, b は付値 v に対して近い、のように考えることができます。

また、付値には次のような「同値関係 \sim{}」が定義できます。付置 v_1, v_2 に対して、 v_1 = v_2^c を満たす c が存在するようなときに v_1, v_2 は同値であるといい、 v_1 \sim v_2 と表します。この同値関係 \sim{} によって、 K の付値全体の同値類の集合を考えるのです。この集合の元、すなわち付値の同値類を素点といいます。

「なんでこんなものを考えるのか」と思ったかもしれませんが、もう少し我慢してください。さて、付値には「アルキメデス的付値」と「非アルキメデス的付値」の２種類があります。説明はしませんが、とにかく２種類あると思ってください。アルキメデス的付値に対応する素点を無限素点、非アルキメデス的付値に対応する素点を有限素点といいます。

面白いのはここからです。実は、 K の有限素点は、 K の素イデアルと１対１対応しています。具体的に、素イデアル \pee から |\cdot |_{\pee} := \pee^{-\text{ord}_{\pee}(\cdot)} という付値を作ることができ、この付値を代表元とする素点が有限素点となるのです。

では、ここで気になるのは「無限素点に対応するものは何だろうか」ということです。その答えは「体の埋め込み」です。複素数体 \mathbb{C} への単射準同型写像 \varphi : K \hookrightarrow \mathbb{C} を考えます。たとえば、 K = \mathbb{Q}(\sqrt{-1}) においては、(1) \sqrt{-1} を \sqrt{-1} に対応させる埋め込みと (2) \sqrt{-1} を -\sqrt{-1} に対応させる埋め込みの２種類があります。ここで、(1), (2) に対応する K の行き先の体を K^{(1)}, K^{(2)} と表すことにします。このような埋め込みは K の自己同型に対応しているので、その個数は n = [K : Q] となることがわかります。また、このような埋め込みの個数は n = [K : \mathbb{Q}] になるという定理があります。

さて、 K^{(i)} が実数体 \mathbb{R} に含まれているとき、 K^{(i)} に対応する埋め込みを「実埋め込み」といいます。逆に、実数体 \mathbb{R} に含まれず、純粋に複素数体への埋め込みになっているとき「虚埋め込み」といいます。上の K = \mathbb{Q}(\sqrt{-1}) の例では、すべての埋め込みが虚埋め込みとなっています。このような K を総虚な体といいます。これが本記事の冒頭で述べた条件だったのです。逆に、すべて実埋め込みの場合は、総実な体といいます。

さて、この埋め込み \varphi から付値を作る方法ですが、 |\cdot| を絶対値記号として、 v(\cdot) = |\varphi(\cdot)|^c とすればよいです。これによって付値が得られ、アルキメデス的付値となります。この付値の同値類が無限素点です。一般に、無限素点は \pee_{\infty} のような記号で表します。

補足：上の例で言うと、 K = \mathbb{Q}(\sqrt{-1}) のときは虚埋め込みが2つあり、対応する付値は2つ・・・と思いきや1つです。なぜかというと、 |z| = |\overline{z}| であるため、複素共役写像の絶対値は元の絶対値と一致して、同じ付値に対応してしまうからですね。一般に K の実埋め込みの個数を s、虚埋め込みの個数を 2t としたとき、 K 上の素点の個数は s+t 個となります。

以上のように素点というものを考えることで、「体の埋め込み」と「素イデアル」を同じ土俵の上で議論できるのですね。


素点を使った類体論の修正ですが、「整イデアル \c」の部分が 「整因子 \c」 と呼ばれるものに変わります。先ほどは、整イデアルとして、分岐する素イデアルを含む素イデアルの有限集合の積を考えていました。これを、分岐する（無限素点を含む）素点の有限集合の積へと変更します。

ただし、ここで２つ注意する必要があります。一つ目は分岐について。無限素点にも「分岐」という概念があります。これについては少し難しいので、今回は割愛します。

もう一つは、無限素点の積をどのように考えたらよいかです。この場合は、有限素点と無限素点を分けて考えます。有限素点はそのまま素イデアルの積をとって、無限素点の方は「形式的な積」をとります。そして、有限素点の積と無限素点の積の「形式的な積」をとるのです。このようにして得られた \c を整因子と呼びます。

これによって、整因子 \c を法とする合同の考え方に、修正が必要となります。例として、整因子を \c = \c_0 \cdot \pee_\infty^{(1)}\pee_\infty^{(2)} とします。 \c_0 は有限素点に対応する素点の積であり、 \pee_{\infty}^{(i)} は埋め込み \varphi^{(i)} に対応する無限素点です。このような \c に対する合同式

\alpha \equiv \beta \pmod{\c}

は、合同式を有限素点と無限素点でばらして、以下のように定義されます：

\alpha \equiv \beta \pmod{\c_0}
かつ \alpha^{(1)} \equiv \beta^{(1)} \pmod{\pee_{\infty}^{(1)}}
かつ \alpha^{(2)} \equiv \beta^{(2)} \pmod{\pee_{\infty}^{(2)}}

ここで、 \alpha^{(i)}, \beta^{(i)} は埋め込み \varphi^{(i)} に対する \alpha, \beta の行き先となります。無限素点の合同式については、以下のように定義されます：

\alpha^{(i)} \equiv \beta^{(i)} \pmod{\pee_{\infty}^{(i)}} \;\; \Longleftrightarrow \;\; \begin{cases} \alpha^{(i)}\beta^{(i)} > 0 & (\pee_{\infty}^{(i)} \text{が実}) \\ \alpha^{(i)}\beta^{(i)} \neq 0 & (\pee_{\infty}^{(i)} \text{が虚}) \end{cases}

つまり、実無限素点の場合は、埋め込みの行き先で \alpha, \beta が同符号であれば合同というわけです。虚無限素点の場合は、非零であれば無条件に合同が成立します。また分岐する素点も、虚の場合は考える必要はありません。そのため総虚な埋め込みの場合は、無限素点を考える必要がなかったというわけですね。これが冒頭で「総虚な」の条件をつけた理由です。

このように考えたとき、 P_K(\c) は

P_K(\c) := \{ (\alpha) \mid \alpha \equiv 1 \pmod{\c} \}

だったので、 \alpha \equiv 1 \pmod{\c_0} かつ \c を割るすべての実無限素点 \pee_{\infty}^{(i)} に対して \alpha^{(i)} > 0 を満たす単項分数イデアル、という条件になります。簡単に言うと、 \alpha を選ぶ条件として、合同式に加えて符号の条件もついたということですね。

具体例：円分体

長かったですが、これで準備は完了です。最後に、 \mathbb{Q} 上のray類体が円分体となることを導きましょう。

まず、 \mathbb{Q} の \mathbb{C} への埋め込みは一つだけです。これを \varphi とおきましょう。 \varphi(\mathbb{Q}) \subset \mathbb{R} なので、 \varphi は実埋め込みです。対応する付値は絶対値関数 |\cdot| となり、この付値に代表される実無限素点を \pee_{\infty} とおきましょう。また、 \mathbb{Q} の有限素点は、素数を p として \pee = (p) で尽くされます。

\mathbb{Q} 上の素点は、素数 p に由来する有限素点と絶対値によって尽くされるというのは「オストロフスキーの定理」の主張です。証明はこちらがわかりやすいです。
mattyuu.hatenadiary.com

したがって、 \mathbb{Q} 上の整因子としては、何がしかの整数 m に対するイデアル (m) と唯一の実無限素点 \pee_{\infty} の積を考えればよいでしょう。

ここでは、例として \c = (m)\pee_{\infty} を法とするray類体 \mathbb{Q}_{\c} を考えましょう。先に答えを言ってしまうと、 \mathbb{Q}_{\c} = \mathbb{Q}(\zeta_m) となります。


私たちは、円分体の理論を知っていて、円分体 \mathbb{Q}(\zeta_m) のフロベニウス \sigma_p が \zeta_m \mapsto \zeta_m^p で表されることを知っています。これは類体論の一般論からは得られない帰結です。
tsujimotter.hatenablog.com

これにより、 \mathbb{Q}(\zeta_m) における素数の分解法則

p \equiv 1 \pmod{m} \;\; \Longleftrightarrow \;\; p は \mathbb{Q}(\zeta_m) で完全分解

がわかります。また、 P_{\mathbb{Q}}(\c) の定義は

P_\mathbb{Q}(\c) := \{ (a) \mid a \equiv 1 \pmod{\c} \}

より、符号分布も考えて a > 0 かつ a \equiv 1 \pmod{m} であるような a の単項分数イデアル全体となります。よって、分解法則は次のように言い換えられます：

(p) \in P_{\mathbb{Q}}(\c) \;\; \Longleftrightarrow \;\; (p) は \mathbb{Q}(\zeta_m) で完全分解

さて、このような条件を満たす \mathbb{Q} 上の拡大体は、ray類体にほかなりませんから \mathbb{Q}(\zeta_m) が法 \c のray類体、すなわち \mathbb{Q}_{\c} = \mathbb{Q}(\zeta_m) が言えました。


また、ray類体の定義より、 \c_{L/\mathbb{Q}} \mid \c であるような \mathbb{Q} 上のアーベル拡大は、すべてray類体 \mathbb{Q}_{\c} = \mathbb{Q}(\zeta_m) の部分体になりますから、以下も言えたことになります。

クロネッカー・ウェーバーの定理
\mathbb{Q} 上の任意のアーベル拡大は，正の整数 m が存在して円分体 \mathbb{Q}(\zeta_m) の部分体となる．

以下の記事で苦労して証明した（まだ証明できていませんが）クロネッカー・ウェーバーの定理が、円分体の分解法則と類体論からあっさりと導かれてしまいました。類体論のパワーを感じますね。
tsujimotter.hatenablog.com


次に同型定理を導くために I_\mathbb{Q}(\c) / P_\mathbb{Q}(\c) を考えましょう。 I_\mathbb{Q}(\c) の定義は

I_\mathbb{Q}(\c) := \{ \c と素な \mathbb{Q} の分数イデアル \}

でしたから、これはそのまま m と素な a に対する単項分数イデアル (a) 全体になります。ただし、 a は整数とは限らないことに注意します。P_\mathbb{Q}(\c) の定義は先ほど述べました。

ここで、実は I_\mathbb{Q}(\c) / P_\mathbb{Q}(\c) \simeq (\mathbb{Z}/m\mathbb{Z})^\times が成り立つのですが、本当に成り立つかどうか、両者の間の同型射 f の存在を議論しましょう。

(a) を I_\mathbb{Q}(\c) / P_\mathbb{Q}(\c) の一つの類 A の代表元とする． (-a) = (a) より、 a > 0 としても一般性は失わない．

このとき，

f(A) = a \pmod{m}

と定義したときに，これが well-defined であることを確認したい．つまり， (a), (b) \in A として異なる代表元をとってきたときに、 f(A) = f(B) であることを確認したい．

また，そもそも a \pmod{m} であるが， a が分数 p/q の場合は、 \bmod{m} における q の逆元 q^{-1} を用いて p q^{-1} \pmod{m} とすればいい．

さて， (b) \in A, \; b > 0 としたときに， (a), (b) は同じ類に属することから， (c) \in P_\mathbb{Q}(\c) が存在して

(c)(a) = (b)

が成立する． c > 0 かつ c\equiv 1\pmod{m} より， ca = b, \; ca > 0, b > 0 と合わせて a\equiv b \pmod{m} である．したがって， f(A) = f(B) より f が well-defined であることがわかる．

また， f が準同型写像であることは明らか．全射・単射性も明らか．よって， f は同型写像を与える．

以上により

I_\mathbb{Q}(\c) / P_\mathbb{Q}(\c) \simeq (\mathbb{Z}/m\mathbb{Z})^\times \tag{13}

が示ました。よって、以下の同型定理がいえます：

円分体の同型定理
(\mathbb{Z}/m\mathbb{Z})^\times \simeq \gal(\mathbb{Q}(\zeta_m)/\mathbb{Q}) \tag{14}

同型定理を使うときにしばしば「（円分体の）類体論より」という枕詞を使うことがありますが、それはこれまでの議論と上の帰結のことを指していたというわけですね。

おわりに

長くなりましたが、これにて終わりです。本記事の内容は、いつかray類体を具体的に計算するときに利用したいと思っています。

また、類体論の証明については、まだ私自身が何も理解していないに等しいので、ブログに書く予定はありません。いつか理解したいです。

それでは今日はこの辺で。

参考文献

今回の記事は、シルヴァーマンの楕円曲線論概説の「虚数乗法」の章を参考にしています。ただし、説明の都合上だいぶ書き換えています。

楕円曲線論概説〈上〉

楕円曲線論概説〈上〉

一方で、上記の本では無限素点の取り扱いについて触れていなかったため、以下を参照しました。

類体論講義 (日評数学選書)

類体論講義 (日評数学選書)

また、 \mathbb{Q} 上の同型定理の計算については、以下の本を参照しました。

類体論へ至る道―初等数論からの代数入門

類体論へ至る道―初等数論からの代数入門

*1:「シュトラール類体」という呼び名もあるそうです。今回はray類体と呼びます。