ストークスの定理

電磁気学やベクトル解析の講義で「ガウスの定理」や「ストークスの定理」「グリーンの定理」という法則を習ったと思います。これらの法則は一見別々のものに見えますが、微分形式を用いるとこれらの法則を統一的に扱えるという素敵なお話を紹介したいと思います。

最近、この話を理解して楽しくなってしまって、自分なりにまとめてみたくなりました。よろしければお付き合いください。

今回の予備知識としては、以下の記事の2章ぐらいまでを読んでおくといいかと思います。
tsujimotter.hatenablog.com

また、「ガウスの定理」や「ストークスの定理」等の定理の主張は知っているものとして進めます。

今日最初に考えたいのは、グリーンの定理です。

グリーンの定理

$(x, y)$ 平面内に（単純閉）曲線 $C$ で囲まれた（単連結な）領域 $D$ があるとき，次の公式が成り立つ：

$\displaystyle \int_C(a dx + bdy) = \int_D \left(-\frac{\partial a}{\partial y} + \frac{\partial b}{\partial x} \right) dx \wedge dy$

ただし，線積分 $\int_C$ は， $C$ 上を反時計まわりの方向に積分する．

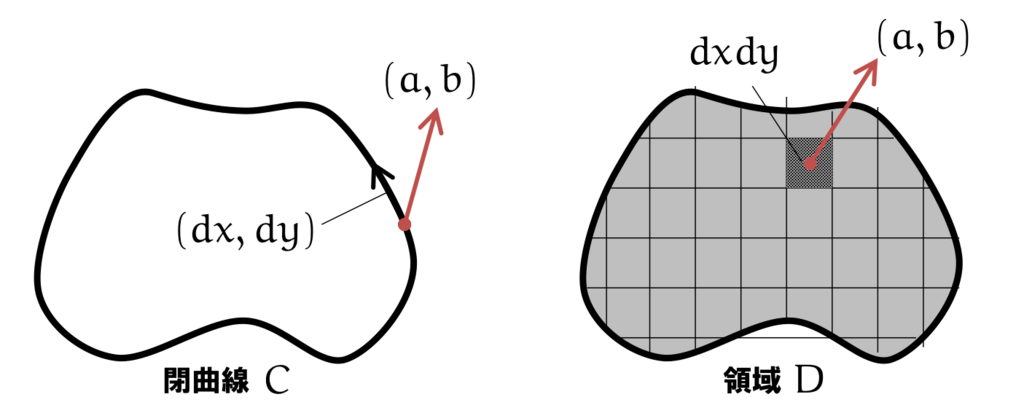
f:id:tsujimotter:20180506181445p:plain:w360

このグリーンの定理は、2次元平面における2通りの異なる積分を結びつける公式です。左辺は曲線の上の「線積分」で、右辺は「面積分」です。面積分に、 $\wedge$ という記号が現れましたが、これは2次微分形式（2-形式）に用いるウェッジ積という記号です。あとで2-形式の定義のときに説明しますが、 $dx \wedge dy$ は単に $dxdy$ と思ってくれてかまいません。ただし、単なる面積を表すのではなく向きも考慮しています。

この公式を簡潔に表すために2次元以上の多様体上の微分形式を考えましょう。

目次：

2次元閉多様体（閉曲面）上の微分形式

3次元閉多様体上の微分形式

ガウスの定理

ストークスの定理

微分積分学の基本定理

まとめ

参考文献

2次元閉多様体（閉曲面）上の微分形式

これまで私のブログで紹介してきた微分形式は0-形式（関数）か1-形式だけでした。2次以上の微分形式が現れなかったのは、我々が1次元の多様体を扱っていたからです。
これから紹介したいのは2次元以上の多様体上の微分形式です。

まずは2次元多様体、すなわち、閉曲面上の微分形式を考えましょう。

2次元多様体を $M$ として、 $M$ 上の開集合を $U, \; V$ とし、それぞれ座標を $(x, y) \in U, \; (s, t) \in V$ としましょう。

f:id:tsujimotter:20180506182839p:plain:w360

それぞれの座標変換のルールは

$\displaystyle dx = \frac{\partial x}{\partial s}ds + \frac{\partial x}{\partial t}dt$

$\displaystyle dy = \frac{\partial y}{\partial s}ds + \frac{\partial y}{\partial t}dt$

となります。

この関係式から、2変数関数 $f(x, y)$ の全微分

$\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$

は、 $(x, y)$ 座標でも $(s, t)$ 座標でも同じ形にかけます。

以下のように計算できます：

$\displaystyle \begin{align} df &= \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy \\ &= \frac{\partial f}{\partial x}\left( \frac{\partial x}{\partial s}ds + \frac{\partial x}{\partial t}dt \right) + \frac{\partial f}{\partial y}\left( \frac{\partial y}{\partial s}ds + \frac{\partial y}{\partial t}dt \right) \\ &= \frac{\partial f}{\partial x} \frac{\partial x}{\partial s}ds + \frac{\partial f}{\partial x} \frac{\partial x}{\partial t}dt + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s}ds + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t}dt \\ &= \left(\frac{\partial f}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s} \right) ds + \left( \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t} \right) dt \end{align}$

連鎖律

$\displaystyle \frac{\partial f}{\partial s} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s}$

$\displaystyle \frac{\partial f}{\partial t} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t}$

より

$\displaystyle \begin{align} df = \frac{\partial f}{\partial s} ds + \frac{\partial f}{\partial t} dt \end{align}$

が得られる。すなわち

$\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy = \frac{\partial f}{\partial s} ds + \frac{\partial f}{\partial t} dt$

が成り立つ。

そこで

$\omega = a(x, y)dx + b(x, y)dy$

という式を考えます。これを1次微分形式（1-形式）といいます。

1-形式は、 $M$ の曲線 $C$ 上で線積分することができます。その定義は、通常の線積分と同様です。曲線 $C$ がパラメータ $u$ により $u_0 \leqq u \leqq u_1$ において $x = x(u), \; y = y(u)$ と表されていれば

$\displaystyle \int_C \omega = \int_{u_0}^{u_1} \left( a(x(u), y(u))\frac{dx}{du} + b(x(u), y(u))\frac{dy}{du} \right)du$

と計算できます。

次に、重積分を定義します。

$D$ が $U \cap V$ の領域のとき、積分 $\int_D f(x, y) dx dy$ を $(s, t)$ 座標で考えるとどうなるか考えましょう。積分の変数変換の公式によれば

$\displaystyle dx dy = \left| \frac{\partial x}{\partial s}\frac{\partial y}{\partial t} - \frac{\partial x}{\partial t}\frac{\partial y}{\partial s} \right| ds dt$

となります。しかし、このままでは絶対値がついていて扱いづらいものとなっています。

この不都合は「負の面積」によって解決できます。つまり、平面上の図形を裏返したら面積は負になると約束し、重積分の定義を変更します。向きを考慮するために、微小面積 $dxdy$ を $dx \wedge dy$ とします。すると、変数変換の公式は

$\displaystyle dx \wedge dy = \left( \frac{\partial x}{\partial s}\frac{\partial y}{\partial t} - \frac{\partial x}{\partial t}\frac{\partial y}{\partial s} \right)ds \wedge dt$

となります。ここで $s = y, \; t = x$ とおくと（ちょうど $x, y$ の立場が反対になるが）、上の公式においては

$dx \wedge dy = - dy \wedge dx$

となります。 $(y, x)$ 平面は、 $(x, y)$ 平面を裏返したものになりますから、それが「負の面積」になるのは直感とも一致しますね。

また、ここで $x = y$ とおくと、 $dx \wedge dx = - dx \wedge dx$ だから

$dx \wedge dx = 0$

とわかります。

一般に $a(x, y) = a(\varphi(s, t), \; \psi(s, t))$ として、 $\omega = a \, dx \wedge dy$ を2次微分形式（2-形式）といいます。このように定義すると、2-形式 $\omega$ は座標系の選び方によらない対称的な形になります。

1-形式のときと同様、2-形式 $\omega$ についての $M$ 上の領域 $D$ 上での積分の値 $\int_D \omega$ が座標系に依存せずに定まります。

さて、ここまで準備すると、グリーンの定理を微分形式を用いて記述することができます。まず、閉曲面 $D$ の境界を $C = \partial D$ と書きます。

実は、この $\partial$ はホモロジーの定義における境界作用素になっています。すなわち、 $D$ は閉曲面 $M$ 上の2-チェインになっていて、 $\partial D$ は $D$ の境界であるような1-サイクルとなります。

次に $\omega = a dx + b dy$ とおくと、これは1-形式になります。ここで、

$\displaystyle d\omega = \left( \frac{\partial a}{\partial x} dx \wedge dx + \frac{\partial a}{\partial y} dy \wedge dx \right) + \left( \frac{\partial b}{\partial x} dx \wedge dy + \frac{\partial b}{\partial y} dy \wedge dy \right)$

と定義します。この $d\omega$ を $\omega$ の外微分といいます。この計算を進めていくと

$\displaystyle \begin{align} d\omega &= \left( \frac{\partial a}{\partial x} \underbrace{dx \wedge dx}_{=0} + \frac{\partial a}{\partial y} dy \wedge dx \right) + \left( \frac{\partial b}{\partial x} dx \wedge dy + \frac{\partial b}{\partial y} \underbrace{dy \wedge dy}_{=0} \right) \\ &= \frac{\partial a}{\partial y} \underbrace{dy \wedge dx}_{-dx \wedge dy} + \frac{\partial b}{\partial x} dx \wedge dy \\ &= \left( -\frac{\partial a}{\partial y} + \frac{\partial b}{\partial x} \right) dx \wedge dy \end{align}$

$d\omega$ は、2-形式となっていて、 $(x, y)$ 座標の代わりに別の $(s, t)$ 座標を使った計算しても、得られる2-形式は同じものになります。つまり、外微分 $d\omega$ は座標に依存しないというわけです。

これらの記号の元に、グリーンの定理は以下のように書き換えることができます：

$\displaystyle \int_{\partial D} \omega = \int_{D} d\omega \tag{1}$

とても綺麗な式になりましたね。説明を加えるとこうなります。

$\displaystyle \underbrace{\int_{\partial D}}_{D \text{の境界（1次元）}} \underbrace{\omega}_{1\text{-形式}} = \underbrace{\int_{D}}_{D\text{（2次元）}} \underbrace{d\omega}_{2\text{-形式}}$

この式は「1次元閉曲線上の1-形式の積分」を「2次元曲面上の2-形式の積分」に変換する公式になっていますね。

さらにいうとこの式は、微分形式の言葉で書かれているので、座標系に依存しません。元々のグリーンの定理は、 $(x, y)$ 座標系に依存した法則でしたが、変形した式ではそうではないのです。したがって、2次元閉曲面においてもそのまま成り立ちます！

単に式変形をして綺麗になったというだけではなく、曲がった閉曲面においても法則を一般化することができたわけです。微分形式すごいです。

実は、同じ法則は3次元閉多様体上、あるいは、一般の $n$ 次元多様体上でも成り立ちます。この法則を（一般化された）ストークスの定理と呼びます。

以下では、3次元の閉多様体上でストークスの定理を考え、「ガウスの定理」や「（ベクトル解析の）ストークスの定理」が出てくることを確かめましょう。

3次元閉多様体上の微分形式

ここからは、舞台を3次元閉多様体に移します。（3次元の図を作るのは大変なので、ここから先は図がありませんがご容赦ください。）

3次元多様体を $M$ として、 $M$ 上の開集合を $U$ とし、それぞれ座標を $(x, y, z) \in U$ としましょう。簡単のため座標系は1つとしておきます。

3次元多様体上では、以下のように 0-形式、1-形式、2-形式、3-形式が定義できます。

$\begin{align} \omega_0 &= f(x, y, z) \\ \omega_1 &= f(x, y, z)dx + g(x, y, z)dy + h(x, y, z)dz \\ \omega_2 &= f(x, y, z)dy \wedge dz + g(x, y, z)dz \wedge dx + h(x, y, z)dx \wedge dy \\ \omega_3 &= f(x, y, z)dx \wedge dy \wedge dz \end{align}$

4-形式以上はすべて 0 となります。また、2次元のときと同様 $dx \wedge dy \wedge dz = - dy \wedge dx \wedge dz$ 等のルールが成り立ちます。

閉曲面のときと同様に外微分を定義すると、次のようになります。

$\displaystyle \begin{align} d\omega_0 &= \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy + \frac{\partial f}{\partial z}dz \\ d\omega_1 &= \left(\frac{\partial h}{\partial y} - \frac{\partial g}{\partial z}\right) dy \wedge dz + \left(\frac{\partial f}{\partial z} - \frac{\partial h}{\partial x} \right) dz \wedge dx + \left(\frac{\partial g}{\partial x} - \frac{\partial f}{\partial y} \right) dx \wedge dy \\ d\omega_2 &= \left( \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} + \frac{\partial h}{\partial z} \right) dx \wedge dy \wedge dz \end{align}$

$d\omega_3$ は4-形式より、 $d\omega_3 = 0$ となることに注意しましょう。

また、 $d(d\omega_0) = 0, \;\; d(d\omega_1) = 0$ となります。

こちらの記事でまとめました：
tsujimotter.hatenablog.com

一般に、外微分を2回行うと必ず 0 になります。これにより「複体」を考えることができます。

参考：
tsujimotter.hatenablog.com

これらの準備の元に、「ガウスの定理」「ストークスの定理」を微分形式の言葉で書き直すことができます。実はその結果の式は、面白いことにグリーンの定理と全く同じ形をしています。

$\displaystyle \int_{\partial V} \omega_2 = \int_{V} d\omega_2 \tag{2}$

$\displaystyle \int_{\partial S} \omega_1 = \int_{S} d\omega_1 \tag{3}$

式 $(2)$ が「ガウスの定理」の言い換えで、式 $(3)$ が「ストークスの定理」の言い換えです。

以下では、これらの公式が私たちの知っている「ガウスの定理」「ストークスの定理」となっていることを確かめてみましょう。

ガウスの定理

まず、ガウスの定理を思い出しましょう。ガウスの定理は、面積分を体積分に変換する公式でした。式 $(2)$ はまさに面積分を体積分に変換する公式になっています。

多様体 $M$ 内に曲面 $S$ で囲まれた領域 $V$ （体積）があれば、 $S = \partial V$ となります。 $S$ にうまく向きを決めると

$\displaystyle \underbrace{\int_{\partial V}}_{V \text{の境界（2次元）}} \underbrace{\omega_2}_{2\text{-形式}} = \underbrace{\int_{V}}_{V\text{（3次元）}} \underbrace{d\omega_2}_{3\text{-形式}} \tag{2再掲}$

が成り立ちます。この式をベクトル解析でよく見かける形に変形してみましょう。

$\omega_2$ は2-形式なので

$\omega_2 = f(x, y, z)dy \wedge dz + g(x, y, z)dz \wedge dx + h(x, y, z)dx \wedge dy$

と表すことができます。これをベクトルの内積を用いて

$\displaystyle \omega_2 = \begin{pmatrix} f, g, h \end{pmatrix}\begin{pmatrix} dy \wedge dz \\ dz \wedge dx \\ dx \wedge dy \end{pmatrix}$

と表します。ここで、 $\boldsymbol{F} = (f, g, h)$ と表すと、 $\boldsymbol{F}$ は $(x, y, z)$ に対応して定まるベクトル場です。また、ベクトル $(dy \wedge dz, dz \wedge dx, dx \wedge dy)$ は、法線ベクトル $\boldsymbol{n}$ と面積素 $dS$ を用いて $\boldsymbol{n}dS$ と表せます。

また、 $\omega_2$ の外微分は、2-形式の外微分の定義より

$\displaystyle d\omega_2 = \left( \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} + \frac{\partial h}{\partial z} \right) dx \wedge dy \wedge dz$

と表せます。これは、 $\boldsymbol{F}$ の発散 $\text{div}\,\boldsymbol{F}$ と、体積素 $dV := dx \wedge dy \wedge dz$ を用いて

$d\omega_2 = \text{div}\,\boldsymbol{F}\, dV$

と表すことができます。

以上より

$\displaystyle \int_{S} \boldsymbol{F}\cdot \boldsymbol{n}dS = \int_{V} \text{div}\,\boldsymbol{F}\, dV$

となって、見慣れたガウスの定理の式が得られました。

なるほど、2-形式の基底 $dy \wedge dz, \; dz \wedge dx, \; dx \wedge dy$ の係数は「ベクトル場」を表していて、その外微分は「ベクトル場の発散」を表していたのですね。

次は、ストークスの定理です。ストークスの定理は線積分を面積分に変換する公式です。

多様体 $M$ 内に曲面があるとき、その上の曲線で囲まれた領域 $S$ 上において

$\displaystyle \underbrace{\int_{\partial S}}_{S \text{の境界（1次元）}} \underbrace{\omega_1}_{1\text{-形式}} = \underbrace{\int_{S}}_{S\text{（2次元）}} \underbrace{d\omega_1}_{2\text{-形式}} \tag{3再掲}$

が成り立ちます。これを変形します。

1-形式 $\omega_1$ を $\omega_1 = f dx + g dy + h dz$ とすると

$\displaystyle \omega_1 = \begin{pmatrix} f, g, h \end{pmatrix}\begin{pmatrix} dx \\ dy\\ dz \end{pmatrix} = \boldsymbol{F}\cdot d\boldsymbol{l}$

と表せます。ここで、 $d\boldsymbol{l}$ は $\partial S$ 上の線素ベクトルです。

また、 $\omega_1$ の外微分は

$\displaystyle \begin{align} d\omega_1 &= \left(\frac{\partial h}{\partial y} - \frac{\partial g}{\partial z}\right) dy \wedge dz + \left(\frac{\partial f}{\partial z} - \frac{\partial h}{\partial x} \right) dz \wedge dx + \left(\frac{\partial g}{\partial x} - \frac{\partial f}{\partial y} \right) dx \wedge dy \\ &= \begin{pmatrix} \cfrac{\partial h}{\partial y} - \cfrac{\partial g}{\partial z}, \cfrac{\partial f}{\partial z} - \cfrac{\partial h}{\partial x}, \cfrac{\partial g}{\partial x} - \cfrac{\partial f}{\partial y} \end{pmatrix} \begin{pmatrix} dy \wedge dz \\ dz \wedge dx \\ dx \wedge dy \end{pmatrix} \end{align}$

ここで、ベクトル場の回転 $\text{rot}\, \boldsymbol{F}$ を用いると

$\displaystyle d\omega_1 = \text{rot}\, \boldsymbol{F} \cdot \boldsymbol{n}dS$

と表すことができます。

最後に $C = \partial S$ と置き換えます。

以上より

$\displaystyle \int_{C} \boldsymbol{F}\cdot d\boldsymbol{l} = \int_{S} \text{rot}\, \boldsymbol{F} \cdot \boldsymbol{n}dS$

となって、見慣れたストークスの定理の式が得られました。

ストークスの定理を習ったときは、 $\text{rot}\, \boldsymbol{F}$ の定義に戸惑ったものですが、これはまさに1-形式の外微分を表していたというわけですね。これならば納得です。

なお、今回紹介したのはどちらも

$\displaystyle \int_{\partial D} \omega = \int_{D} d\omega \tag{4}$

という形の法則でしたが、これらは一般の次数の微分形式に対しても成り立ちます。このような法則を総称してストークスの定理と呼びます。ベクトル解析では、線積分を面積分に変換するものをストークスの定理と呼んでいましたが、これは、一般に成り立つ大きな法則の一部分だったというわけです。

微分積分学の基本定理

せっかく微分形式の説明をしてきたので、最後にもう一つだけ面白い話を紹介します。

ストークスの定理は、任意の次元の多様体で成り立ちます。1次元の多様体で考えたらどうなるでしょうか。1次元においては、0でない微分形式は0-形式と1-形式しかありませんので、0-形式 $\omega_0$ に対するストークスの定理

$\displaystyle \int_{\partial D} \omega_0 = \int_{D} d\omega_0$

を考えます。 $D$ としては、1次元多様体の点 $A, B$ を結ぶ閉区間 $AB$ を表すことにします。

この式の意味を考えましょう。 $D$ を含む座標近傍 $U$ を考えて、座標を $x$ とします。点 $A, B$ はそれぞれ座標を使って $x = a, x = b$ と表します。

f:id:tsujimotter:20180506190518p:plain:w220

0-形式 $\omega_0$ は関数より、 $\omega_0 = F(x)$ と表せます。また、外微分は $d\omega_0 = F'(x) dx$ と表せます。これらを代入すると

$\displaystyle \int_{\partial D} F(x) = \int_{D} F'(x) dx$

となりますね。あとは、この積分の意味を考えればよいでしょう。

まず、右辺は閉区間 $[a, b]$ の線積分なので

$\displaystyle \int_{a}^b F'(x) dx$

とすればよいですね。

一方で、左辺は少し考える必要があります。 $D = AB$ を $A\to B$ の方向に向きが入った 1-チェインと考えて、これに境界作用素 $\partial$ を適用すると

$\partial D = B - A$

となり、 $0$ -チェインとなります。 $B - A$ に対する積分を自然に

$\displaystyle \int_{B-A} \omega_0 := \int_{B} \omega_0 - \int_{A} \omega_0$

として定義すると、左辺の積分は

$\displaystyle \int_{B} \omega_0 - \int_{A} \omega_0$

となります。点 $A, B$ における 0-形式（関数）の積分は、その点の関数値になりますから、左辺の積分は

$\displaystyle F(b) - F(a)$

とできます。

よって

$\displaystyle F(b) - F(a) = \int_{a}^{b} F'(x) dx$

が得られました。

この式は「定積分は、積分区間の両端における原始関数の値の差 $F(b) - F(a)$ に一致する」ということを表しています。これはまさに微分積分学の基本定理そのものですね！

つまり、微分積分学の基本定理は、ストークスの定理の1次元における特殊な場合だったというわけです。面白いですね。

まとめ

長い記事でしたので、今日お話したことをまとめておきましょう。

微分形式には一般化されたストークスの定理という法則があって、これは

$\displaystyle \int_{\partial D} \omega = \int_{D} d\omega$

という形の式でかけるのでした。

ベクトル解析や電磁気学で習った「グリーンの定理」「ガウスの定理」「ストークスの定理」、さらには「微分積分学の基本定理」までもが、ストークスの定理によって表すことができたのです。以下のようにまとめることができます。

多様体の次元	微分形式	定理
1	0-形式	微分積分学の基本定理
2	1-形式	グリーンの定理
3	2-形式	ガウスの定理
3	1-形式	ストークスの定理

ストークスの定理を微分形式を用いて一般化する利点は、単に法則が統一的にかけるというだけではありません。微分形式によって記述することで、座標系によらないために、ユークリッド空間に限らず一般の可微分多様体においても成り立つ法則となるのです。元々の定理は「平らなユークリッド空間」に限定された法則だったわけですが、微分形式を使って書き直したことで「一般の曲がった空間」へと拡張できてしまったのです。これはすごいことだと思います。

最後に、ストークスの定理を少し違った視点から見てみましょう。

$k$ -形式 $\eta$ に対して、もし $\eta = d\omega$ となるような $(k-1)$ -形式 $\omega$ が存在すれば、ストークスの定理の左辺と右辺を入れ替えて