ニコニコ学会β 第8回シンポジウムにて,tsujimotter が披露し好評を博した「触れるゼータ関数」がついに発売!
今まで触れることができなかった「ゼータ関数」があなたの手に!
冒頭からテンションの高い文章となっていますが,ついにあのゼータ関数を,皆様の手にお届けする準備が整いました!
ニコニコ生放送でも放送されたニコニコ学会βのシンポジウムで,tsujimotter はゼータ関数の魅力を凝縮してご紹介しました。
日曜数学の成果として,作品をいくつかご紹介したわけですが,その1つが「触れるゼータ関数」だったのです。
まだ見ていないという方は,まずはニコニコ生放送のアーカイブで辻の発表をご覧ください。
第8回ニコニコ学会βシンポジウム~現実性を超えて~@ニコニコ超会議2015[DAY2] - 2015/04/26 10:00開始 - ニコニコ生放送
発表を見てくださった方の中には,ゼータ関数がほしくてたまらない という方もおられるかと思います。
こうした皆様に,「触れるゼータ関数」を提供する方法を模索しておりましたが,この度 DMM.make にて公開することになりました。
DMM.makeに「クリエイターズマーケット」というコーナーがあります。これは,自作の3Dデータを投稿すると,そのデータを出力した作品を商品として販売してくれるんですね。公開されている商品をオンライン上で注文すると,3Dプリンタによってオンデマンドで出力され,自宅まで届けてくれるというものです。
「触れるゼータ関数」は,こちらのサイトに出品しています。目的に合わせてフルエディション・ミニエディションの2パターンご用意しています。
触れるゼータ関数(フルエディション)
まず,最初に公開したのがこちらの商品!
「触れるゼータ関数(フルエディション)」 です。
触れるゼータ関数(フルエディション) - DMM.make クリエイターズマーケット
X, Y方向を複素平面の実部・虚部とし,Z方向にそのゼータ関数の絶対値 をプロットしています。ただし,高さ方向は 5 倍に強調しています。
このフルエディション,非自明なゼロ点が,なんと 20 個 *1 もあるんです!
実部の範囲は ,虚部の範囲は
となっています。
もちろん,すべての非自明なゼロ点は,実部が 1/2 の直線(クリティカル・ライン)の上にのっていますよ。
この作品は「ナイロン」で出力できますが,ナイロン出力の上限サイズは 65cm です。フルエディションでは,この最大サイズに設定しました。
いやー,迫力ありますね!
部屋の一番目立つ場所に飾りたい!
お値段は 298,999 円!もちろん 素数 です。
最大サイズで最大限にゼロ点を詰め込んだ結果、こんなお値段になってしまいました。これは数学を心から愛する私でもちょっと手が届かない・・・。
というわけで,数学を愛する石油王のご購入をお待ちしています。笑
触れるゼータ関数(ミニエディション)
上のバージョンでは「ゼロ点がちょっと多すぎるな」という方におすすめしたいのが,次にご紹介する 「ミニエディション」 です。
触れるゼータ関数(ミニエディション) - DMM.make クリエイターズマーケット
こちらは,虚部の範囲が となっており,ゼロ点の個数も 6 個です。実寸サイズも,最大 6 cm と手のひらに収まるサイズになっています。
カラーバリエーションも豊富で,全部で9色の中から選ぶことが出来ます。
お値段は,ホワイトであれば 4,447 円,その他のカラーだと 4,999 円。もちろん,どちらも 素数 です。
ちょっとお安い石膏のバージョン (4,001 円) もございますよ。
場所をとらないサイズ感なので,机の上に飾ってみてもいいでしょう。数学の勉強が捗ること間違いなし。
今まで手が届かないと思っていたゼータ関数が,手の上に乗っかっているのです。これはテンションが上がらないはずがありませんね。
自明なゼロ点
ところで,このデータを作る過程で,ちょっとした発見があったのです。
ゼータ関数には,非自明なゼロ点のほかに,実軸上に自明なゼロ点が存在します。 のように,負の偶数上の点においてゼータ関数がゼロをとることは 自明 なので,「自明なゼロ点」と呼ばれているのですね。
とはいえ,この部分の周辺領域はどこも起伏が小さいので,ゼロ点があっても気づかないだろうと思っていたのです。
ところが,ほら,ここみてください!
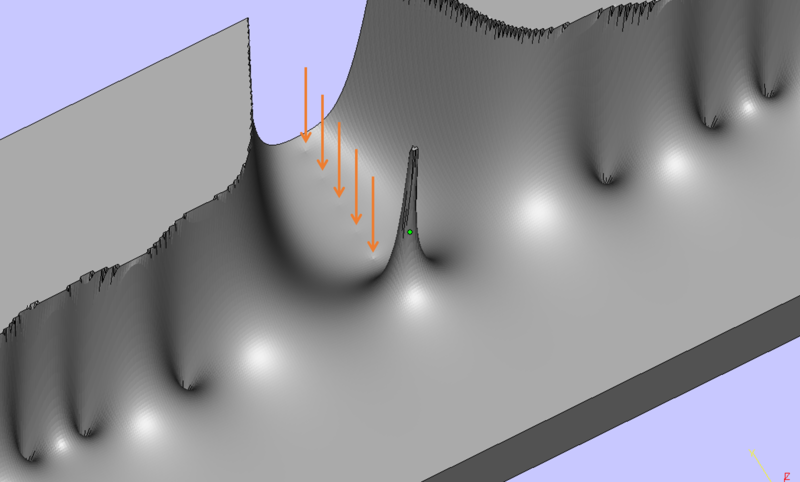
ちゃんと負の偶数の位置が凹んでいるでしょう!これは,どうみてもゼロ点ですね!!
たとえ数式で理解したと思っていても,実際に見るとまた違った喜びがあります。
「触れるゼータ関数」を通して,このような発見と感動をたくさんの人に味わってもらいたいですね。
購入特典(フルエディションのみ)
フルエディションの方,非常に魅力的でなのですが,ちょっとお高いのでなかなか手が出せないですよね。
とはいえ,もしかしたらご購入を希望する石油王がいるかもしれませんので。笑
万が一お買い求めいただいた方のために購入特典を用意してみました。
「tsujimotterに数学を語ってもらえる券」です。私がふだん数学に使っている,大切な日曜日をひとつあなたに捧げたいと思います。
実際,このようなゼータ関数を買ってくれる方は,おそらくよほど数学が大好きな方なので,ぜひお会いしてお話ししたいという気持ちもあります。笑
日時・内容はご相談ください。
それでは,ご注文お待ちしております。
レポート記事
id:yumu19 さんにレポート記事を書いていただきました。サイズ感や触り心地など参考になる情報がまとまっています。
yumulog.hatenablog.com
id:jurupapa さんにもレポートを書いて頂きました!「手触り感のある数学」という表現、素敵ですね!
maxima.hatenablog.jp
参考ページ
ニコニコ学会の出演レポートです。
今回のゼータ関数は,tsujimotter の独自開発のライブラリによって計算されました。仕組みについて,こちらで解説しています。
ゼータ関数と素数の関係についてはこちら。
*1:ただし,複素共役を重複して数えています。

