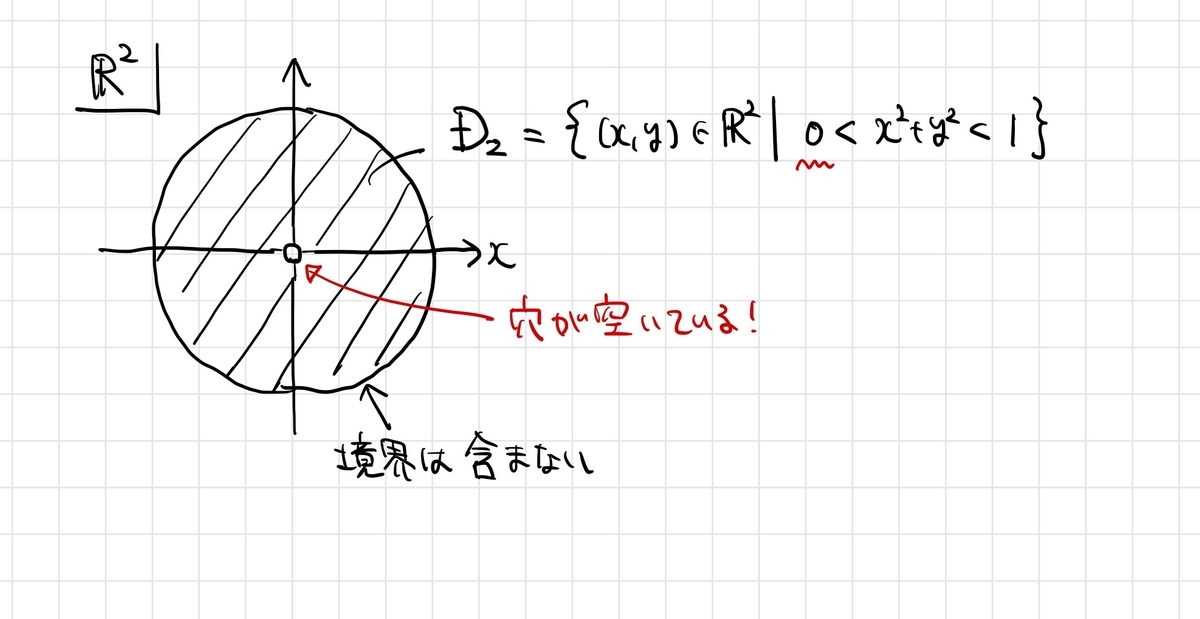
上の記事では、穴あき円板  上のド・ラームコホモロジー
上のド・ラームコホモロジー  を計算しました。
を計算しました。
ド・ラームコホモロジーを計算するには、 上の任意の閉1形式(
上の任意の閉1形式( の元)を計算し、それと完全1形式(
の元)を計算し、それと完全1形式( の元)との「差」(実際は商ベクトル空間)を計算する必要があります。
の元)との「差」(実際は商ベクトル空間)を計算する必要があります。
このとき、非自明な元
が存在して、 が閉1形式でありながら完全1形式ではないことを示しました。
が閉1形式でありながら完全1形式ではないことを示しました。
前回の記事では、「ド・ラームの定理」という非常に大きな定理を使うことで、 の
の  上の次元が1であることを示し、結果として
上の次元が1であることを示し、結果として  が1次元の基底をなすことを示したのでした。
が1次元の基底をなすことを示したのでした。
しかしながら、ド・ラームの定理を使うのはちょっと大掛かりすぎますね。もっと直接的に示す方法はないものかと思っていました。そんな折に、ラスクさん( @washoi4150 )という方からTwitterで「直接的に示す方法はあるよ」と教えていただけました。
そこで今回は、ラスクさんに許可をいただきまして、 上のド・ラームコホモロジーのより直接的な計算方法を紹介したいと思います。
上のド・ラームコホモロジーのより直接的な計算方法を紹介したいと思います。
常々思っているのですが、ブログを書いて公開することによって、自分自身が一番勉強になっています。
私自身は独学で数学を勉強しているので、本に書いてない内容についてはただただ自分の頭で考えるしかないのですが、どうしてもわからずに断念してしまうことが多々あります。なので、私の知らないアイデアをより詳しい人に提供いただけるのは、本当にありがたいことです。
独学で数学を勉強していて、私と同じように悩んでいる人はいるのかもしれません。私のケースがどれぐらい一般化できるのかは分かりませんが、「自分がここまで理解したぞ」という部分を、ブログなりSNSなりで(理解が完全でないことを承知の上で)アウトプットしてみるというのも悪くはないのではないかなと思っています。*1
今後もこういったコミュニケーションを大事にしながら、勉強を進めていきたいと思っています。
それでは内容に入っていきましょう!
続きを読む