銅錯体が青いのはなぜか。その化学的な理由を突き止める記事 後編 です。
今回はいよいよ 群論 が登場します! 「対称性」を使って色の仕組みがどのように理解できるのか!?

前編の内容を前提に進めますので、ご覧になっていない方はまずはこちらをご覧ください:
tsujimotter.hatenablog.com
目次:
1. 点群:群を使って分子の対称性を理解する
前編の記事では、あくまで直感的に2価の銅イオンの錯体が青色になる仕組みを説明しました。そこでは 錯体の「分子の形」 と、銅イオンの「d軌道の形」 が鍵となりました。少し振り返ってみましょう。
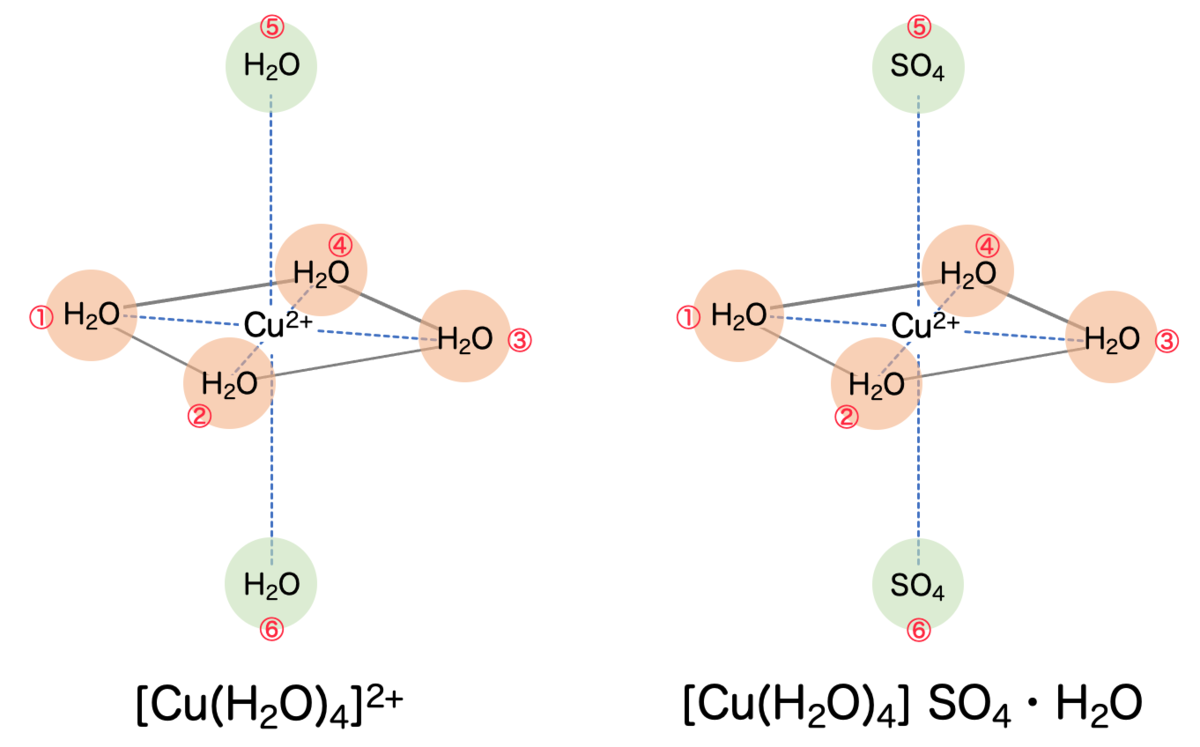
分子の形については、水溶液の銅(Ⅱ)イオン も、硫酸銅(Ⅱ)五水和物の結晶
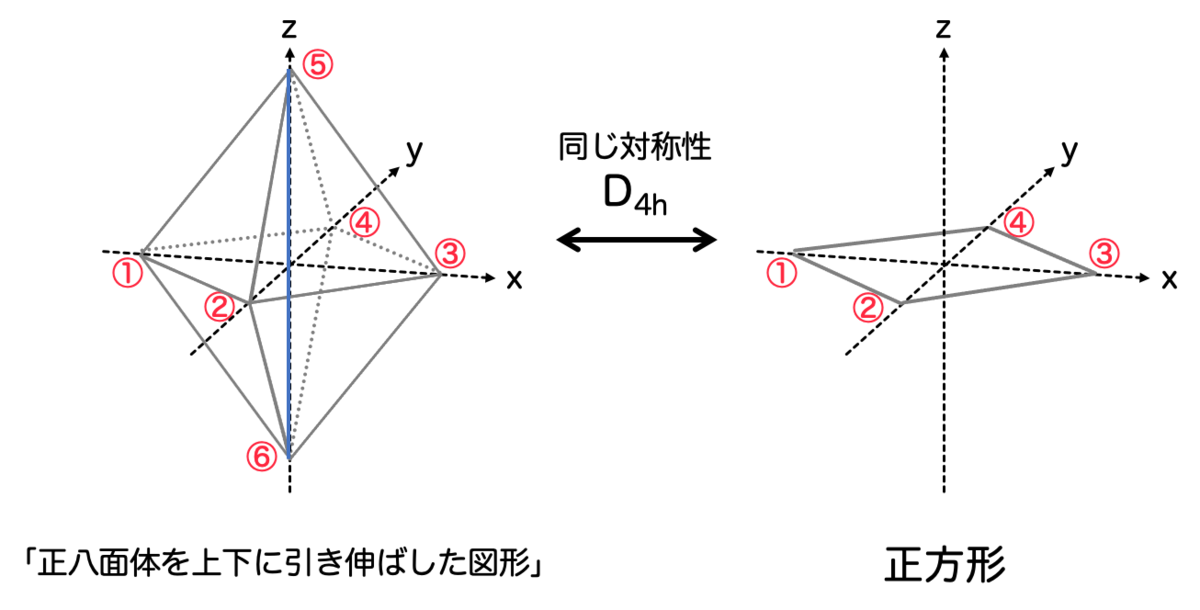
も、いずれも八面体の構造をしていました。正八面体ではなく、正八面体を上下に引き伸ばした形ということでした。
また、d軌道の形状については、その違いによって八面体の頂点に配置された配位子からの静電場の影響に違いが生じるのでした。それによってエネルギー差が生まれ(縮退が解け)、結果としてそのエネルギー差に対応する光を吸収できる、ということでした。
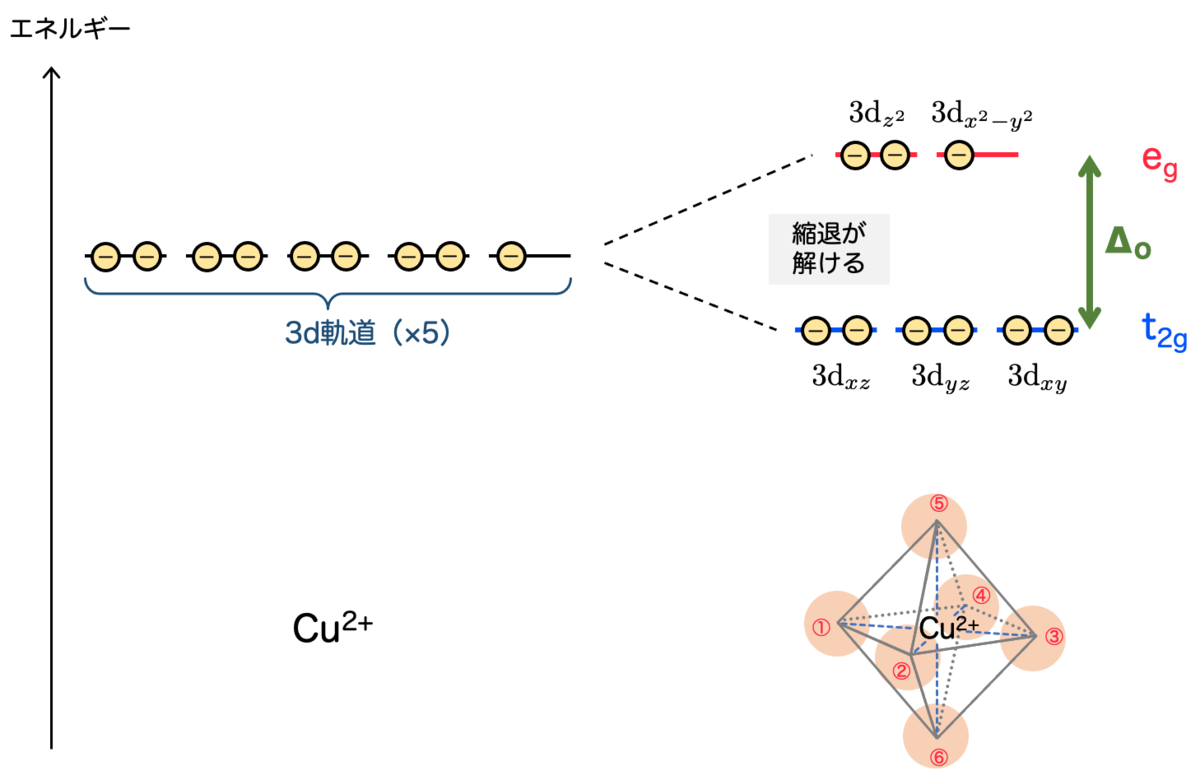
しかし、この議論を正確に実行するためには(エネルギー差が生じることを説明するためには)、摂動論なりを使って実際にシュレーディンガー方程式を解く必要が出てきます。それはなかなか大変です。
ところが、図形の対称性を使うと、シュレーディンガー方程式を実際に解かなくても縮退が解けることが示せる のです。この節では、その説明を試みてみましょう。
「対称性」という言葉は割と日常的に使う言葉だと思いますが、幾分ふわっと用いられることが多いかと思います。これを数学的に記述する道具が 「群」 です。
たとえば、正三角形は対称的な図形ですが、具体的には次の6つの操作に対して対称的です:
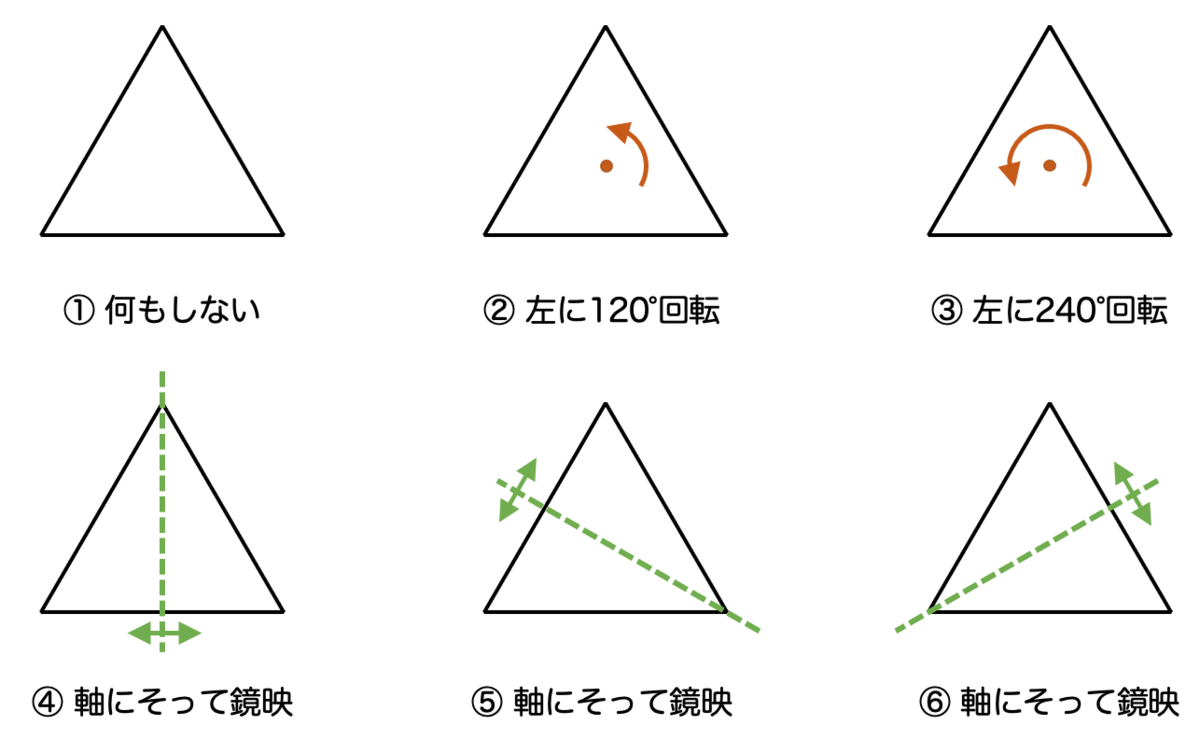
図形の対称性を「対称的な操作全体の集まり」として定義するのがポイントです。
より一般に、2次元や3次元の図形 を考えたとき、図形
の形を変えないような操作を考えます。そのような操作全体の集合
を 図形
の対称性の群 といいます。
(このとき、恒等操作「何もしないという操作」も含めます。)
操作の間には「操作を合成する」という演算が備わっています。つまり、 という操作と
という操作を連続して適用することにより
という操作を得ます。(操作の合成は左から掛けることに注意します。)この演算も含めて群の要件となっています。
演算した結果得られた新しい操作は、元の操作の集合 に属している必要があります。たとえば、正三角形の場合は「120°回転」と「240°回転」という操作がありますが、これらを合成して得られる「360°回転」は「何もしないという操作(恒等操作)」と同じです。だから、
に恒等操作を入れる必要があったわけですね。
今回考えたい対称性は、分子の構造についての対称性 です。
3次元においては
を考えることができます。これに加えて、次の②〜④も考えます:
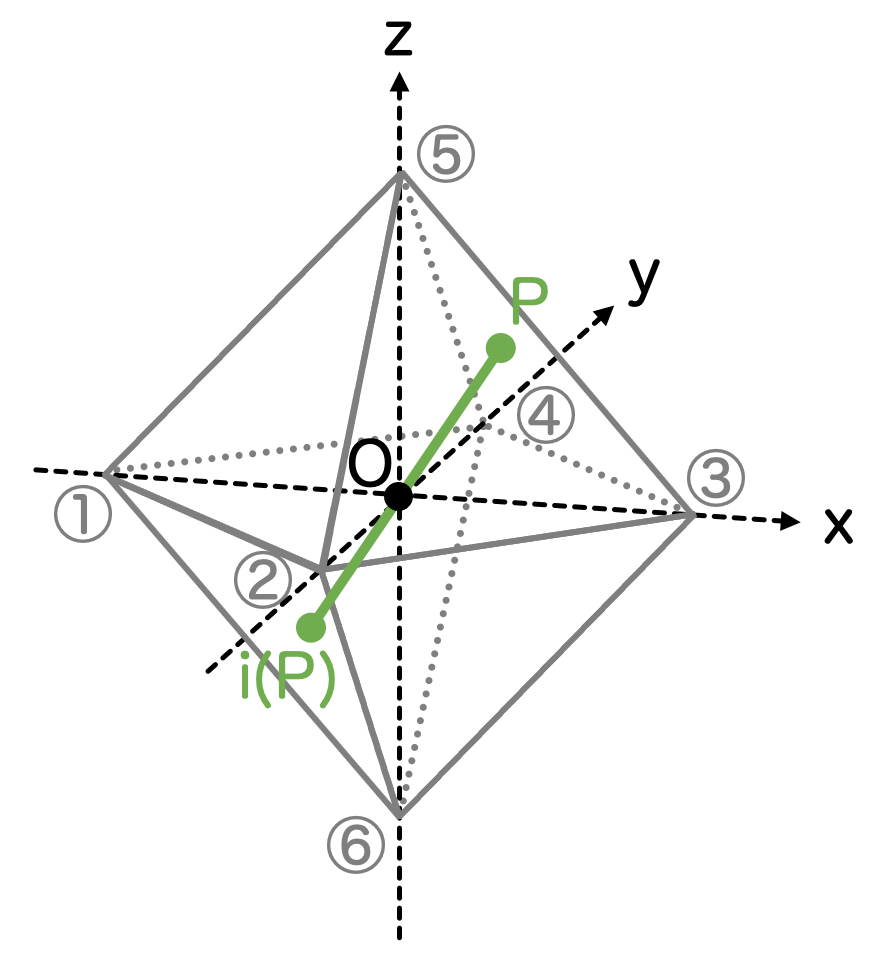
③ 反転操作(点に対する反転)
④ ①〜③を合成して得られる操作
3次元の図形 に対して、
について①〜④の対称的な操作を考えます。このような操作全体の集合を 点群 といいます。
錯体化学においては、錯体の3次元構造を図形と見立てて点群を考えます。これが錯体の化学的性質を説明するのに使えるのです。
2. 正八面体配位の点群 Oh
具体的に、硫酸銅の水和物の分子構造について点群を考えたいと思います。
硫酸銅の水和物は 「八面体(正八面体を上下に引き伸ばした図形)」 の頂点に配位するのでした。
もちろんこのままで硫酸銅の水和物の議論にはなっていません。一番対称的なケースを考えておくことで、対称性が崩れたケースも考えやすくなるのです。
一通り正八面体の議論を実行したあとで、最後に「八面体(正八面体を上下に引き伸ばした図形)」についても考えたいと思います。
正八面体には 計48個の対称的な操作 があり、この点群には という名前がついています。
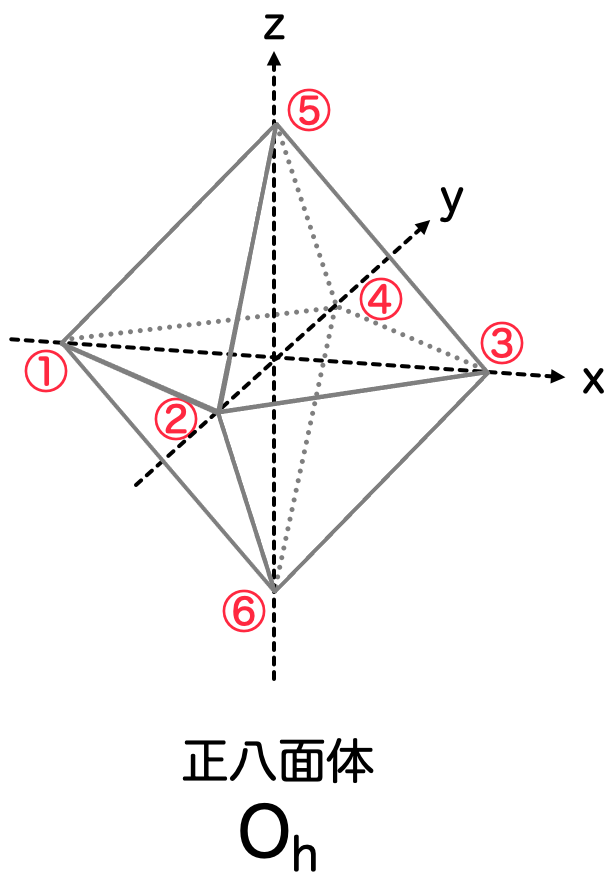
一方「正八面体を上下に引き伸ばした図形」については、「正方形」と同じ対称性を持っていると考えることができます。この点群には という名前がついていて、
は16個の対称性を持っています。
今から に属する48個の対称性を、全部列挙したいと思います。
といっても、種類としては実質8種類しかないので、頑張れば列挙できます。やってみましょう。
- 恒等操作 E (× 1)
まずは、何もしないという操作です。この操作を と表記することにしましょう。
- 3次回転操作 C3 (× 8)
正八面体の「面」は正三角形である点に着目します。中心を挟んで向かい合う2つの面を考えます。面の中心を結ぶ直線を考えて、この直線の周りを左回りに120°回転、240°回転させることができます。
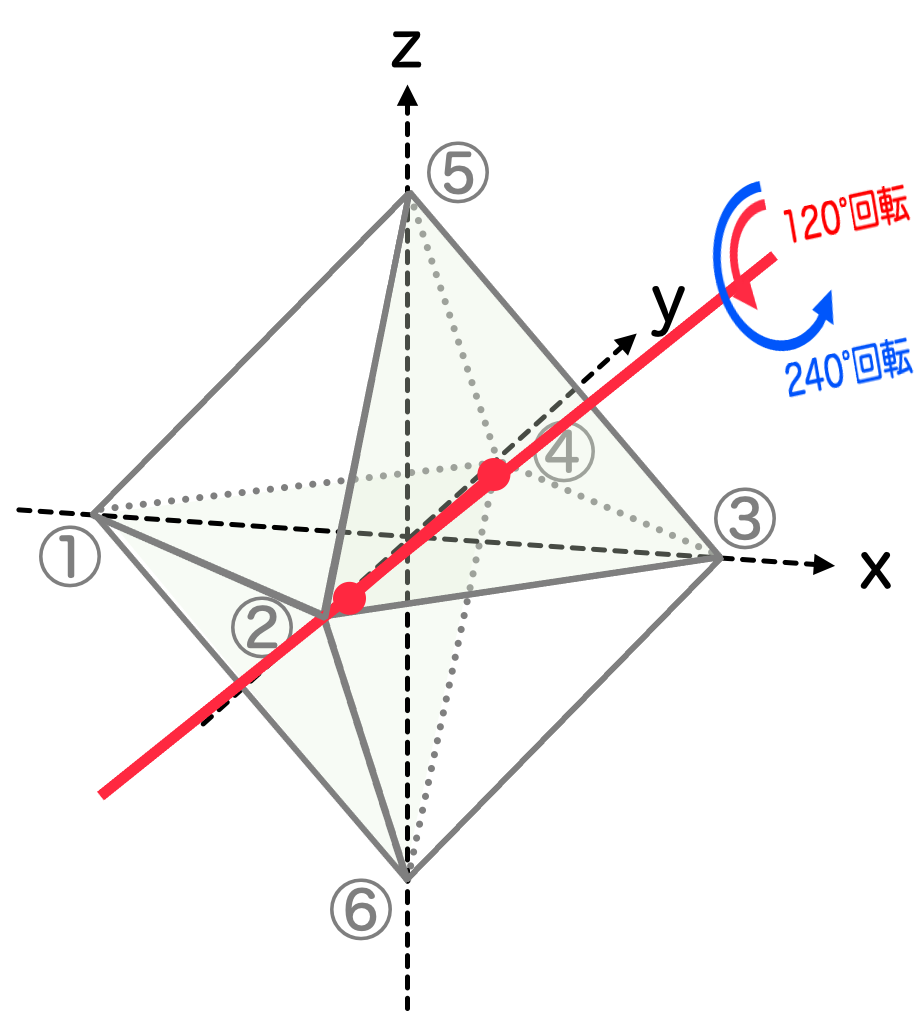
面の組は全部で 個あり、それぞれ
個ずつの対称操作があるので、計
個の対称性があることになります。
- 2次回転操作 C2 (× 6)
今度は正八面体の「辺」に着目しましょう。向かい合う辺を取り、辺の中点同士を結ぶ直線を考えます。この直線で180°回転させることができます。
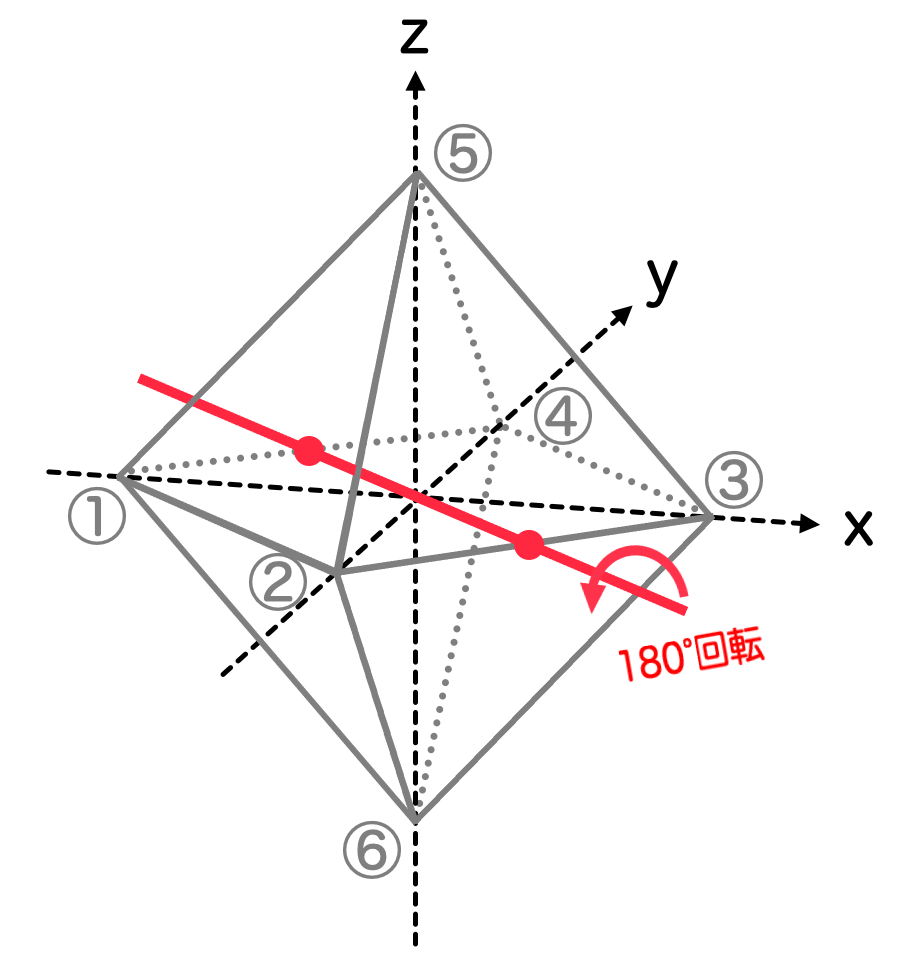
辺の組の個数は 個なので、計
個の対称性があることになります。
- 4次回転操作 C4 (× 6)
次は正八面体の「頂点」に着目しましょう。向かい合う2頂点に対して、2頂点を結ぶ直線を考えます。この直線で90°・270°回転させることができます。(180°回転もあるのですが、これは次に数えます。)
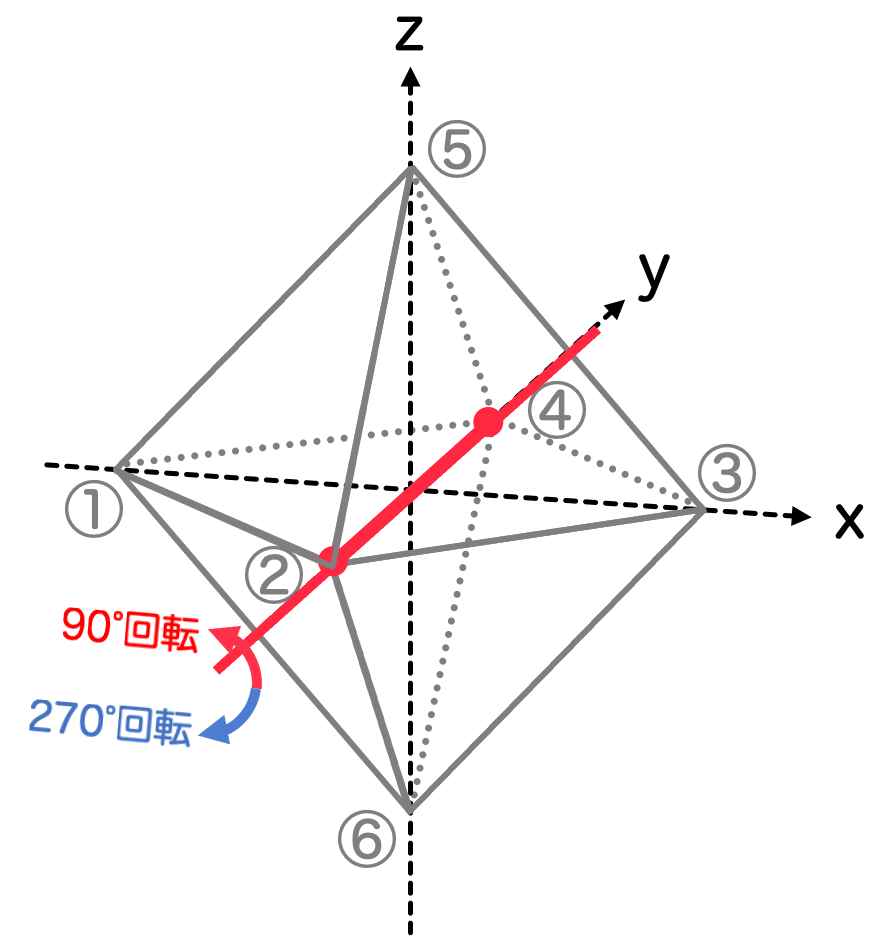
頂点の組の個数は 個なので、計
個の対称性があることになります。
- 2次回転操作 C2 (× 3)
同じく頂点に着目すると、頂点を結ぶ直線で180°回転させることができます。頂点の組の個数が 個なので、
個の対称性があります。
- 中心に関する鏡映操作 i (× 1)
空間上の各点を、中心の座標に関して点対称な位置に移動させる操作を考えます。これを 個の対称性とカウントします。
- 4次の回転鏡映操作 S4 (× 6)
回転鏡映とは、その名の通り回転操作と鏡映操作を合成した操作のことです。ここで、向かい合う2頂点を通る直線を考えて、90°あるいは270°回転させます。その後、直線と原点で直交する平面を考えて、その平面に関する鏡映を実行します。
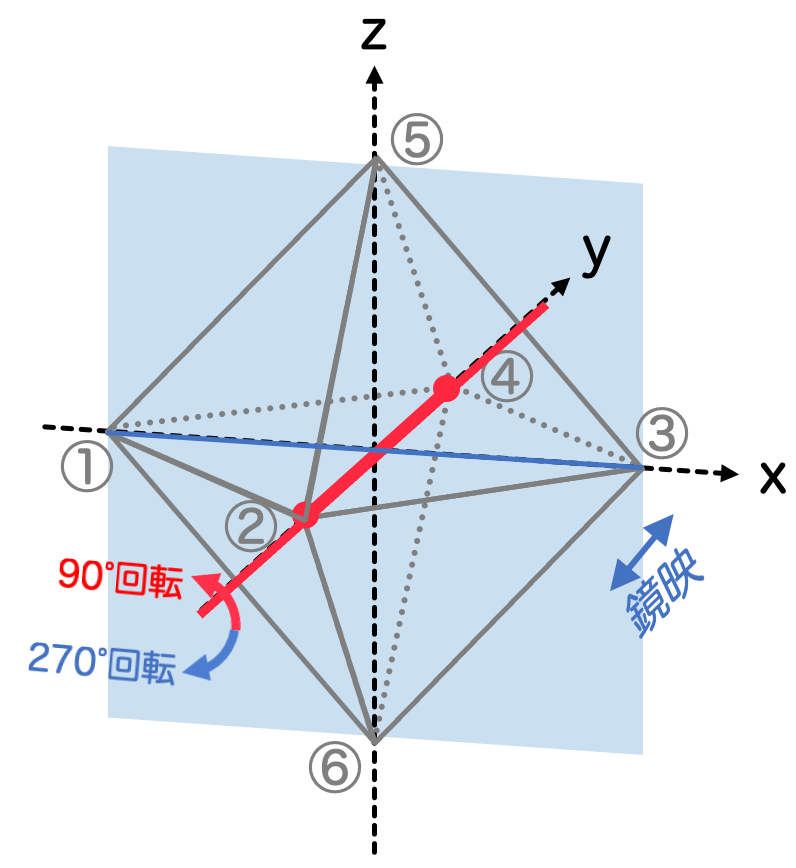
向かい合う頂点の組の個数は 個あるので、対称性の個数としては計
個あります。
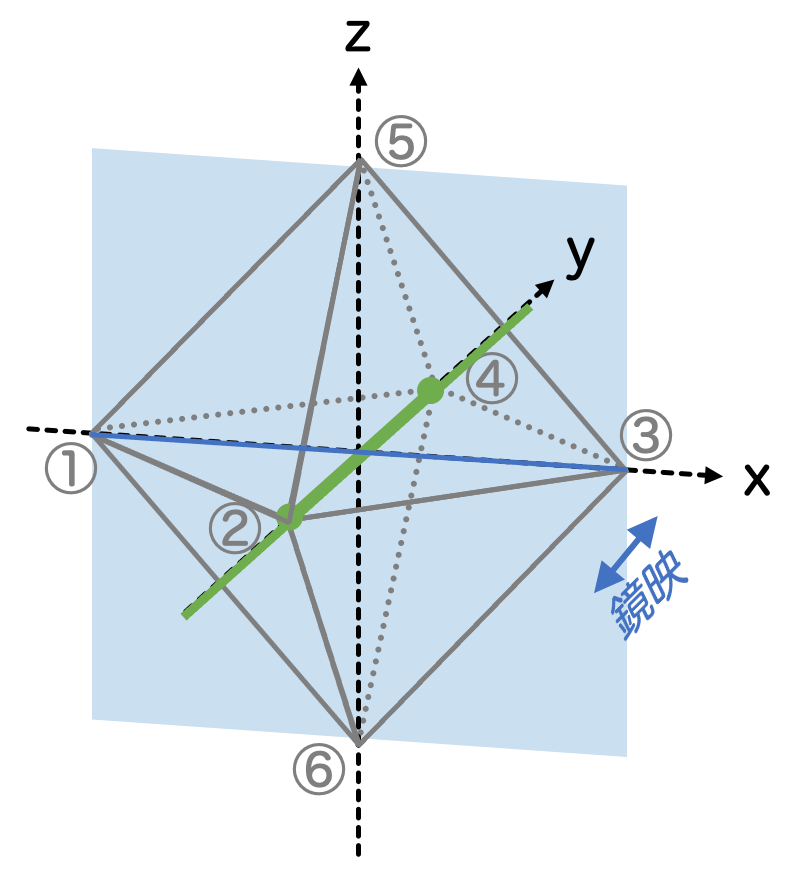
- 2次の回転鏡映操作 S2 (×8)
向かい合う面の中点に対して、同じように回転鏡映を考えます。すなわち、向かい合う2つの面の中心を通る直線を考えて、直線を120°あるいは240°回転させます。その後、直線と原点で直交する平面を考えて、その平面に関する鏡映を実行します。
向かい合う面の組の個数は 個あるので、対称性の個数としては計
個あります。
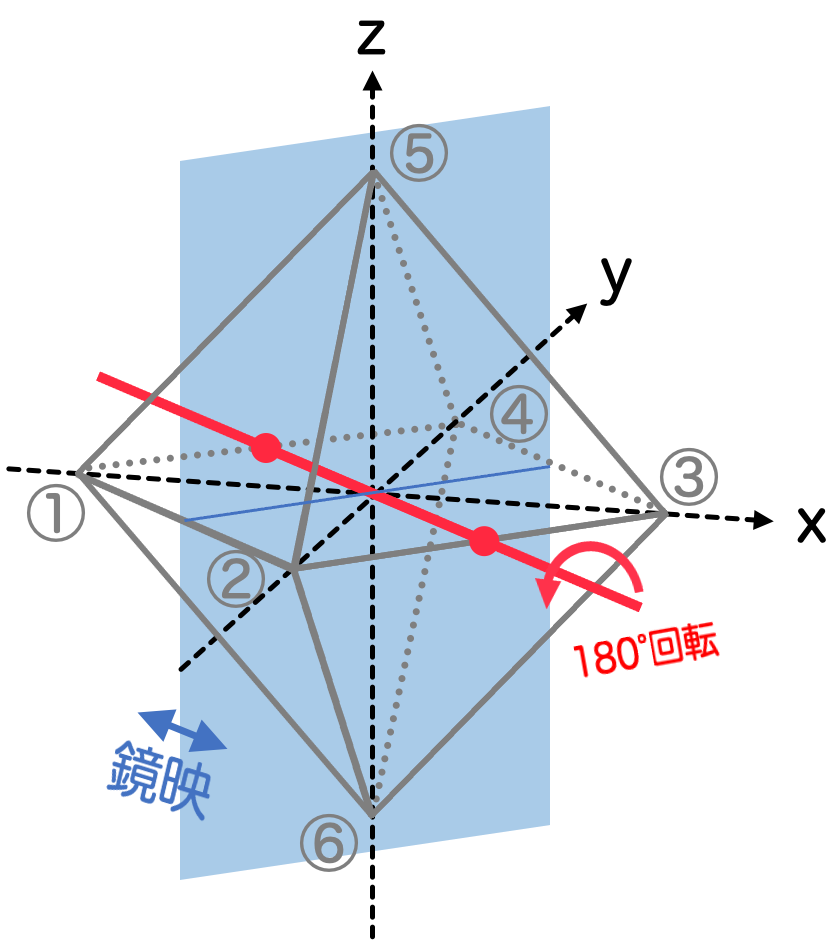
- 面に関する鏡映操作 σh (×3)
向かい合う2頂点を結ぶ直線を考えます。この直線と原点で直交する面を考えて、この面に関する鏡映を考えます。
向かい合う頂点の組の個数は 個あるので、対称性の個数としては計
個あります。
- 面に関する鏡映操作 σd (×6)
向かい合う2辺の中点を結ぶ直線を考えます。この直線と原点で直交する面を考えて、この面に関する鏡映を考えます。
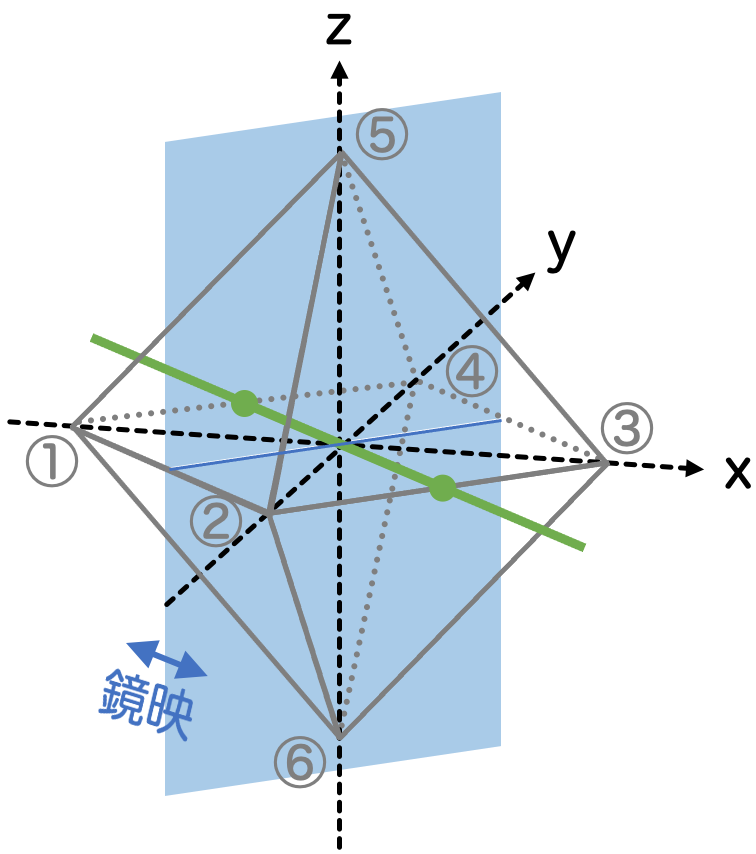
向かい合う辺の組の個数は 個あるので、対称性の個数としては計
個あります。
まとめると、次のようになります:
| 対称性 | E | C3 | C2 | C4 | C2 | i | S4 | S2 | σh | σd |
|---|---|---|---|---|---|---|---|---|---|---|
| 対称性の個数 | 1 | 8 | 6 | 6 | 3 | 1 | 6 | 8 | 3 | 6 |
よって、正八面体の点群の要素数は
で 個ということになります。いやー、数えるだけでなかなか大変ですね。
3. シュレーディンガー方程式の対称性と点群
このセクションの説明に誤りがありましたので、説明の流れを変更しました。
さて、点群 (正八面体の対称性の群)が計算できましたが、これがどうして錯体の性質の解明につながるのでしょうか。
点群 の要素を1つ選んで
としましょう。
は正八面体の分子に作用させることができます。
を作用させると、各配位子の場所が入れ替わるだけで、元の分子と配置はまったく変わりません。
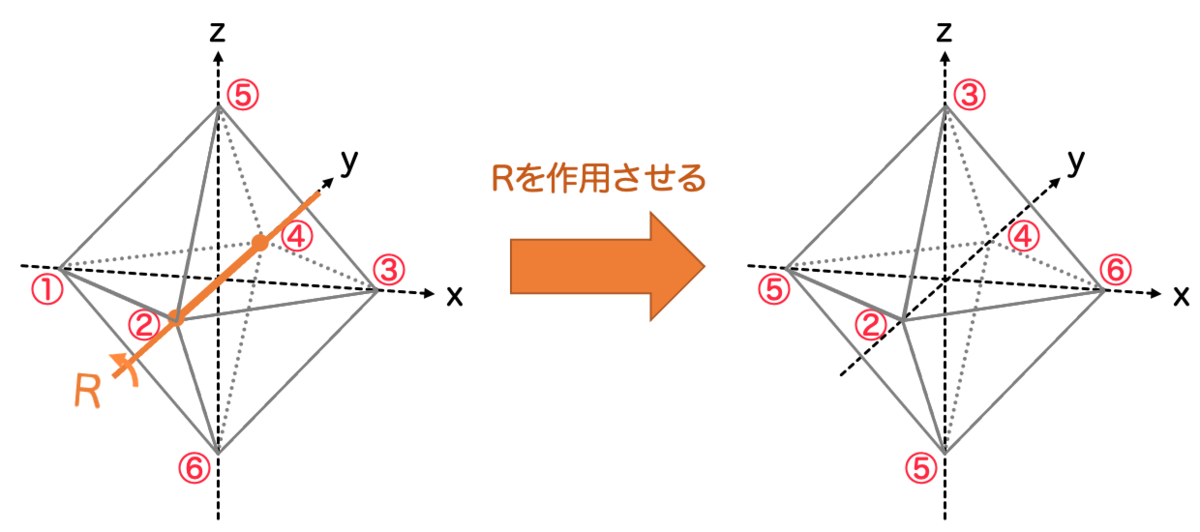
相対的な位置が変わらないということは、ハミルトニアンも変化しません。(ここがポイント!)
今は分子の骨格だけ考えましたが、今度は波動関数に を作用させてみましょう。
ハミルトニアンを として、固有値
の波動関数を
とすると
が成り立ちます。
波動関数 に
を作用させます。すると、
は(分子はそのままに)波動関数を
によって変換させたものになります:
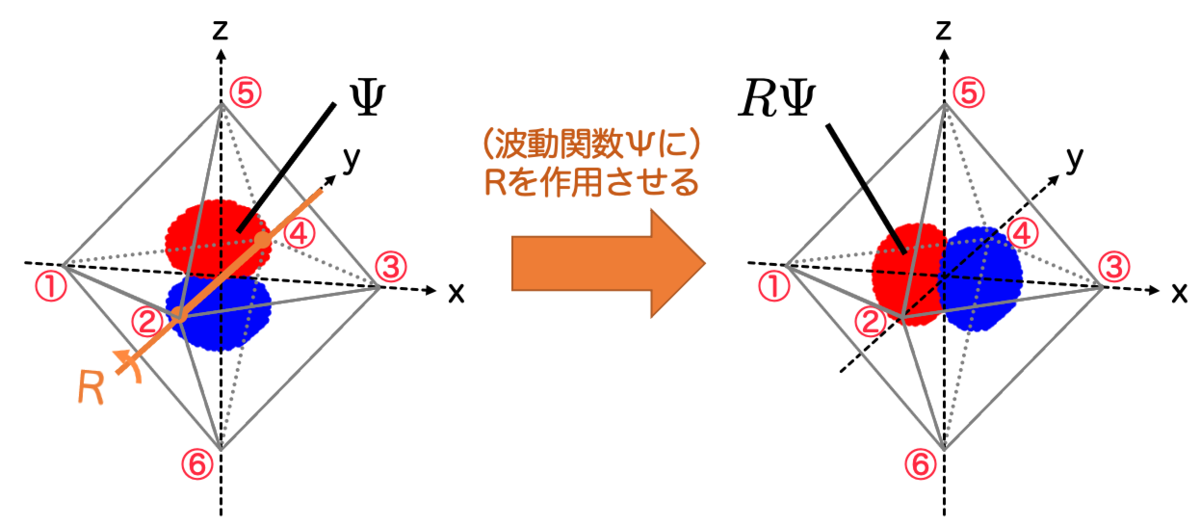
分子と波動関数をまとめて で変換すると、元々の分子と波動関数と同じ状況になります(分子の対称性)。このことから、波動関数
も同じエネルギー
を持つことがわかります。つまり
ということです。
となります。この式の両辺に を作用させると
が得られます。
式 よりこれは
なので
が成り立つということになります。このことを「 はハミルトニアン
を不変にする」と言ったりします。
あるいは、別の言い方をすると
が成り立つということになりますが、これは「 と
が可換である」ということを意味します。
どちらも、点群の要素 が分子の構造に対して対称的であることの帰結です。
さて、式 は大変面白いことを言っています。
今私たちは、波動関数同士が縮退しているかどうかに興味があるわけです。ところが、点群を作用させて得られる波動関数は、同じエネルギーを持つ、つまり縮退していることがわかるというわけですね。
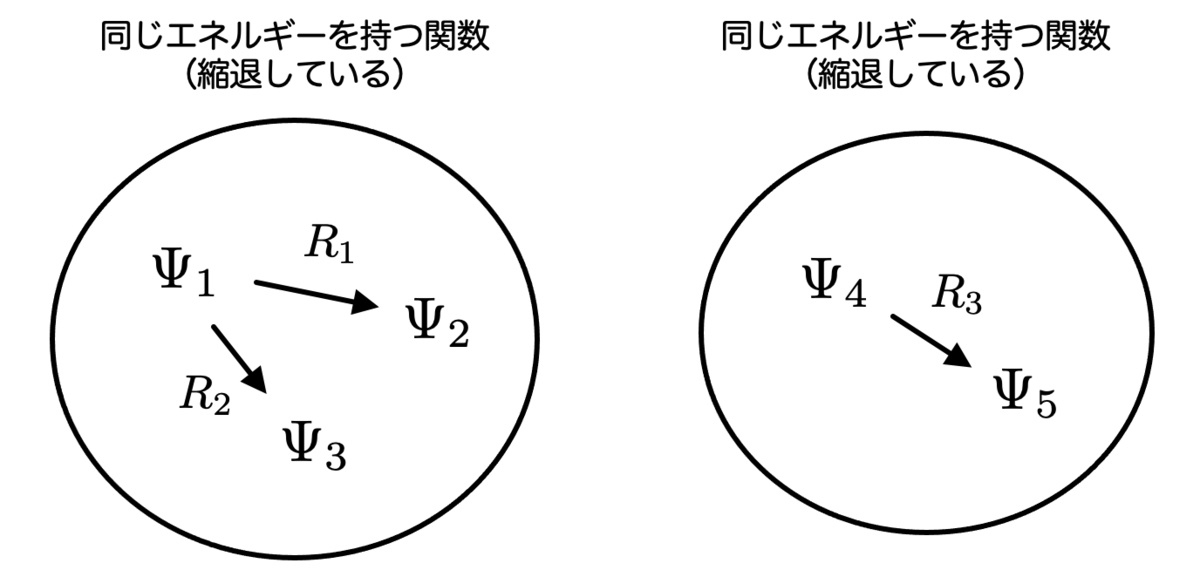
これを使うと、5つの3d軌道のうち3つが同じエネルギーを持つ(つまり縮退している)ことがただちに分かってしまいます。
以下では、3d軌道の5つの波動関数をそれぞれ
と表記します。
と表していましたが、係数と紛らわしいので "3" を省略するということです。図の中では、前編と同じ表記をしているものも一部混じっています。
波動関数の具体的には次のような形であったことを思い出しましょう:
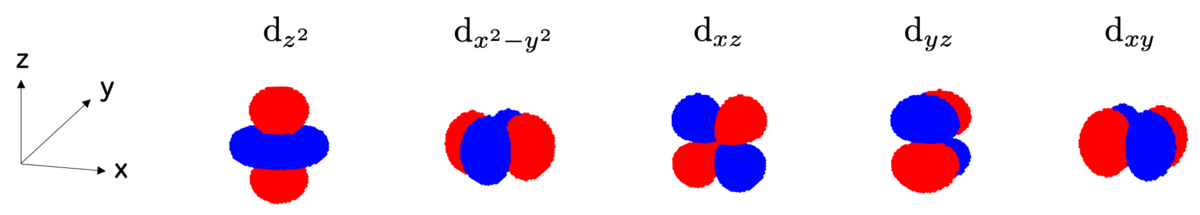
以下では、 が縮退していることを、点群
によって示します。
具体的に、 の2つの要素
- 頂点⑤⑥を通る直線のまわりで左90°回転させる操作:
- 頂点①③を通る直線のまわりで左90°回転させる操作:
を考えましょう。この操作を施すと、 は
を用いて
と表せます。
図に表した方がイメージしやすいかもしれません:
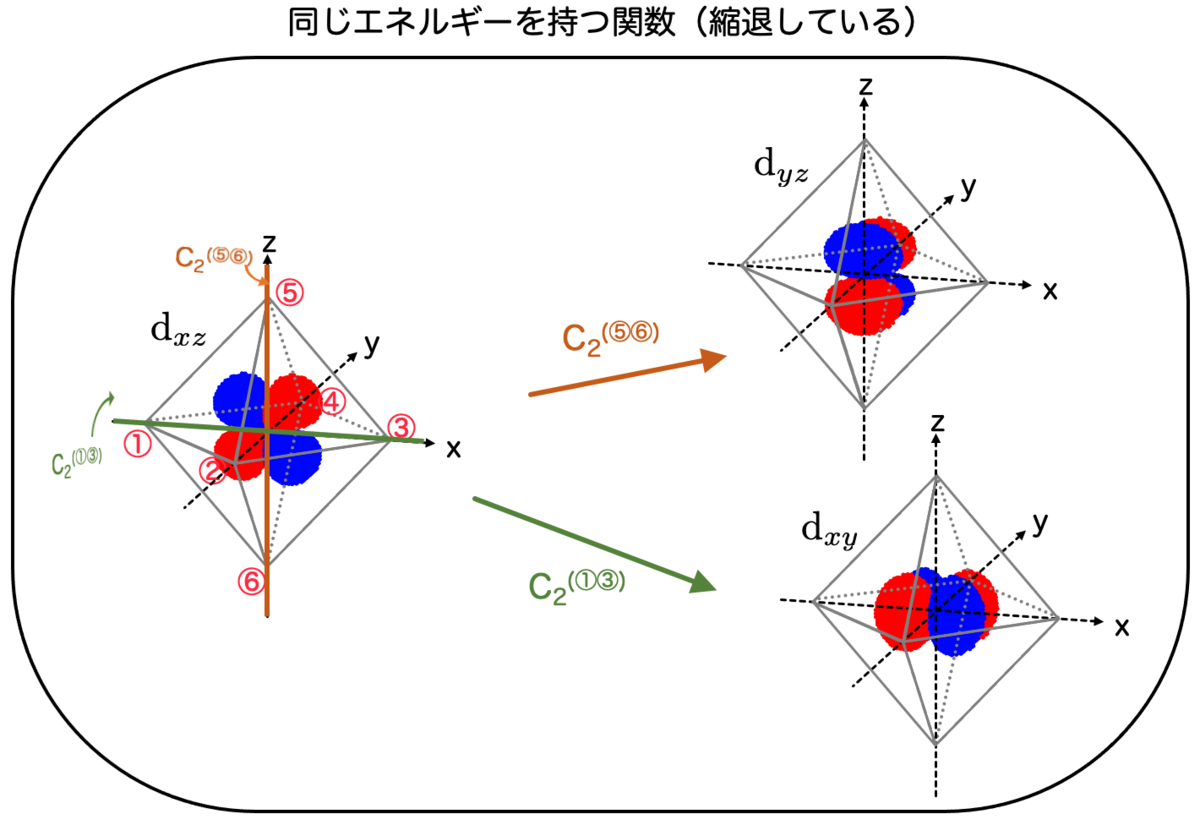
d軌道の対称性だけで が縮退していることが分かってしまいました。
いよいよ面白くなってきましたね!対称性を列挙した甲斐があります!
まとめると、シュレーディンガー方程式のハミルトニアンを動かさない変換を考えて(点群)、それを軌道に作用させることで、軌道が縮退しているかどうか調べることができる、ということです。これが基本的な方針です。
これまでの議論で、波動関数の縮退について、次の枠内の条件を与えることができました。
これだけでも点群の恩恵は十分あったといえそうです。
一方、このままではまだ
も縮退していること
と
が異なるエネルギーを持つこと
については分かりません。
この問題について、次の節では 群の表現、特に 既約表現 という言葉を使って整理してみたいと思います。
4. 群の表現:点群による3d軌道の変換を行列で表す
点群 (正八面体の対称性の群)の操作を一つ選んで
とします。
今、同じ固有値 を持つ固有空間の
個の基底
を考えます。
に対して具体的に計算することになります。
しばらく抽象的な議論が続きますが、上の具体的なケースを頭に思い浮かべながら読んでいただければと思います。
一般に、上と同じ固有値 に対して
を満たす任意の関数 (つまり
の固有関数)は
と表せるということですね。このような関数全体のなすベクトル空間を と表します。
式 を念頭に入れながら、今考えている基底
それぞれに、点群の操作
を作用させます。
前節の式 で議論したように、
に
を作用させた
も
となり、同じ固有値 を持つ固有関数になっているのでした。したがって、基底を用いて
と表されるはずです。
このことはすべての基底 (
)に対して成り立つので、
本の式
が得られます。行列を使って表すと
ということです。右辺の行列を としましょう。
つまり、点群 の操作
に対して、
次の行列
を対応させることができたというわけです。
こんな風に、群の要素に対して行列を割り当てることを 群の表現 といいます。「表現」という名がついている通り、群の要素のことを行列で「表現」しているわけですね。
ですが、細かいところは置いておきましょう。
上では、固有値 に対応する固有空間
を考えました。今度は、別の固有値
に対して、固有空間
を考えます。
とします。
ここで、 と
の基底を並べて得られるベクトル空間
を考えます。これをベクトル空間
と
の直和といい、
と表します。
ベクトル空間の直和 に対しても、両者の基底全てに対して操作
を作用させれば、上とまったく同じ手順で
次の行列が得られます。
ここで、 の基底に
を作用させたときに、その結果に
の基底は出てきません。逆も然りです。
よって、 の
に対する表現行列を
とし、
に対する表現行列を
とすると、
に対する
の作用は次のように表せます:
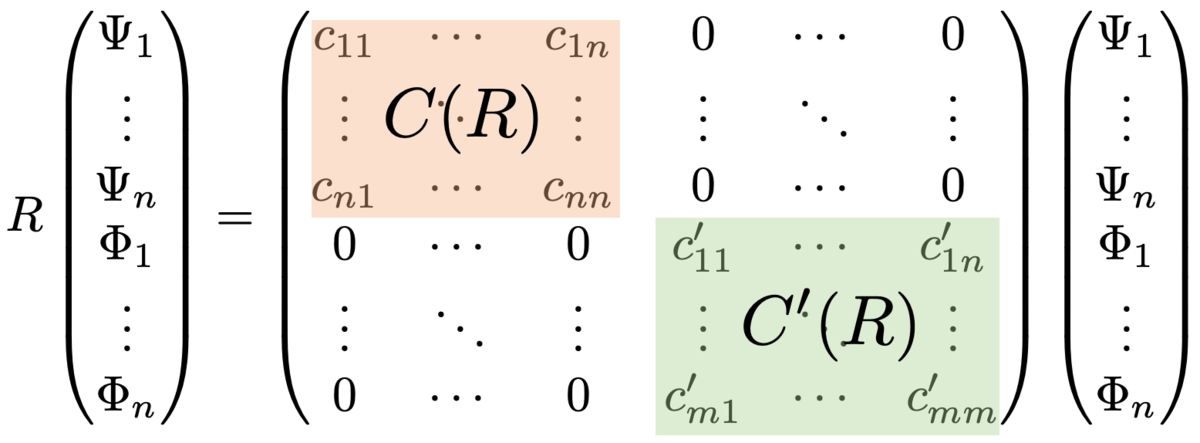
ここから新しい表現

が得られます。
逆に、点群のすべての操作 に対して表現行列
が同じ形の小ブロックに分けられるとき、
の作用を小ブロックごとに分けることができます。
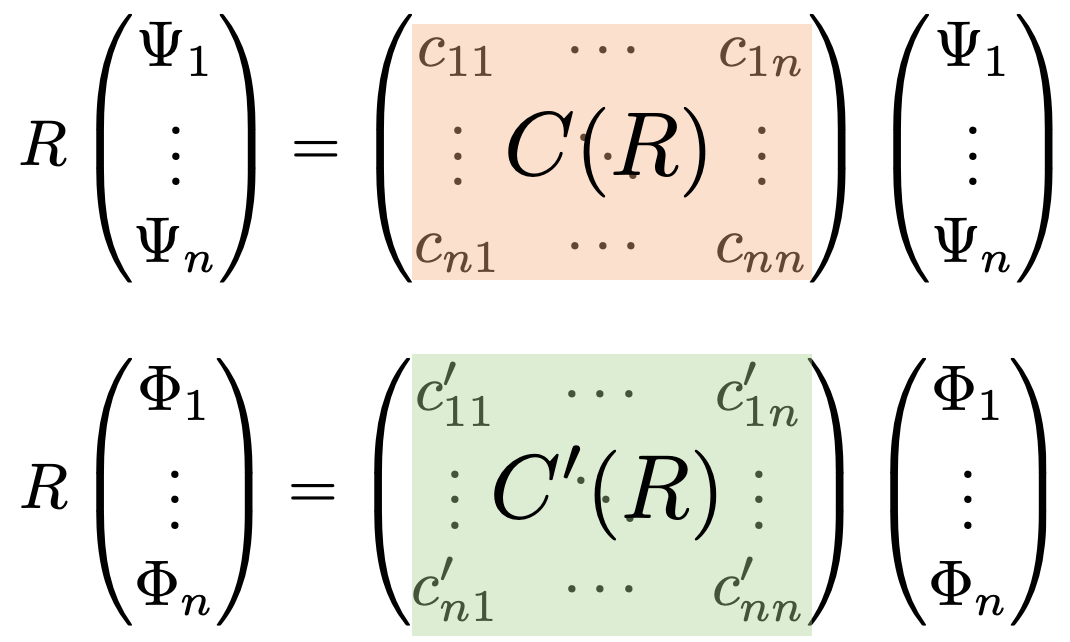
このように、任意の において表現行列
が同じ形の小ブロックに分解できる表現のことを 可約表現 といい、これ以上分解できない表現のことを 既約表現 といいます。
正確にいうと、可約には見えない表現であっても、基底を変換することで可約にできる場合があります。
だったとします。これは対角行列ではないとします。
これに対して、 の基底をある行列
で変換します:
基底をこのように変換させたとき、表現行列は という形になります。
任意の に対して、行列
がすべて対角行列
になるのであれば、2つの空間に分けられるわけです。このような場合も可約であるといってよいのです。
そんなわけで、どのように基底を変換させても2つの空間に分けれないとき、既約表現であるというわけです。
さて、既約表現という言葉を使って、元の問題を整理してみましょう。
まず 、次のことがわかります:
(証明)もし仮にエネルギーが と表せる部分空間
が存在して
と表せたとする。すると、
の基底へ群を作用させたときに得られる関数は固有値
なので、
の基底は出てこない。逆も然り。したがって、
によって得られる表現が可約となってしまい、既約性に反する。(証明おわり)
また、逆方向もだいたい成り立ちます。
つまり、物理に出てくるような系においては、対称性などの特別な理由がない限り「エネルギーが等しい(縮退している)ならば既約表現」が成り立つというわけです。逆に言えば、可約表現なのに偶然縮退しているというケースはレアケースということですね。
まとめると、エネルギーが等しい(縮退している)固有空間を特定するためには、既約表現を探せばよい ということになります!
このことはシュレーディンガー方程式を直接計算せずに実行できるのです! 群論すごい!!
「エネルギーが等しい(縮退している)ならば既約表現」が必ず成り立つような書き方をしていましたが、誤りでしたので修正させていただきました。
5. 点群 Oh の表現の具体的計算
では、実際に3d軌道の空間 に対して、点群
の表現を計算してみましょう。
計算の過程で必要になるので、3d軌道の各波動関数を具体的に記述しておきましょう。
まず思い出していただきたいのは、波動関数を計算する方法です。「日曜化学(1)」と「日曜化学(2)」では座標をデカルト座標系 から球面座標系
に置き換えたのでした。
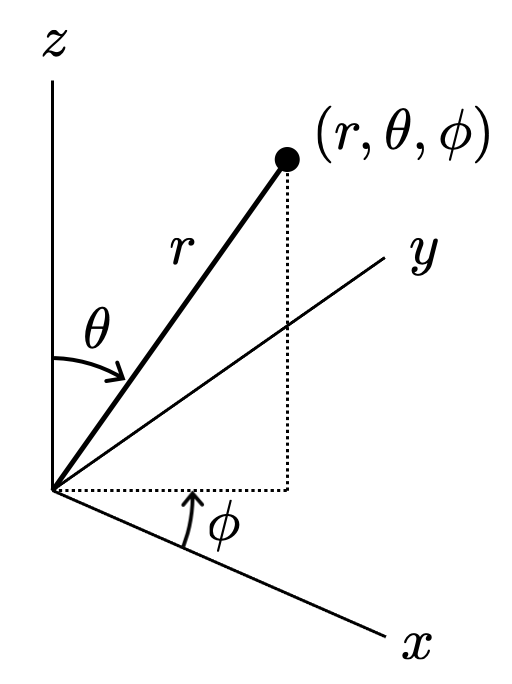
から
への座標変換の公式は、次で与えられます。
この座標系において、波動関数は のように変数分離して計算できるのでした。ここで、
は動径波動関数で、
は球面調和関数です。
動径波動関数 は「日曜化学(2)」で紹介したように一見かなり複雑です。しかし、3d軌道(すなわち、量子数
の場合)だけを考えるのであれば、思い切り省略して
と表すことができます。
球面調和関数も具体的に計算すると、結局3d軌道の波動関数は次のように表示できます:
ずいぶん複雑だなと思う人もいるかもしれません。私もそうだったのですが、実は再度 の座標変換を施すと、関数の形が劇的に簡単になることに気づきました。
実際、次のように計算できます。
に関する係数
を見なかったことにすると
となります。これでようやくd軌道の添字についていた記号の意味が理解できましたね!
また、これから3d軌道に点群 を作用させるわけですが、
は
を作用させても変換しません。
は定数だと思って問題ないわけですね。したがって、係数
の部分はなかったことにして計算したいと思います。
このような準備の元、点群 の元を
に作用させていきましょう。
Eの表現行列
まず一番簡単な (恒等変換)による作用を考えましょう。座標
への作用は
となります。「何もしない変換」なので当たり前ですね。
これを3d軌道に作用させると、次のようになります:
これも当たり前ですね。
行列によって表すと
となりますから、結局
という対応が得られたことになります。
こんな要領で計算していきます。全部計算するのは大変なので、例としてあと2個だけ計算しましょう。
C2の表現行列 (1)
次に (向かいあう辺の中点で180°回転)の作用を考えます。
は全部で6個ありましたが、今回は図のように
平面上で
となるような直線について計算したいと思います。

このような操作をここでは と表記することにします。座標
への作用は
となります。
これを3d軌道の基底に作用させます。一個ずつ計算していきましょう。(簡単のため係数 は省略します。)
よって、まとめるとこうなります。
したがって、 の表現行列が
と求められたというわけです。
C2の表現行列 (2)
最後に、 からもう一つ変換操作を考えたいと思います。
今度は図のように 平面上で
となるような直線を考えて、この直線に対して180°回転させる変換を
とします。
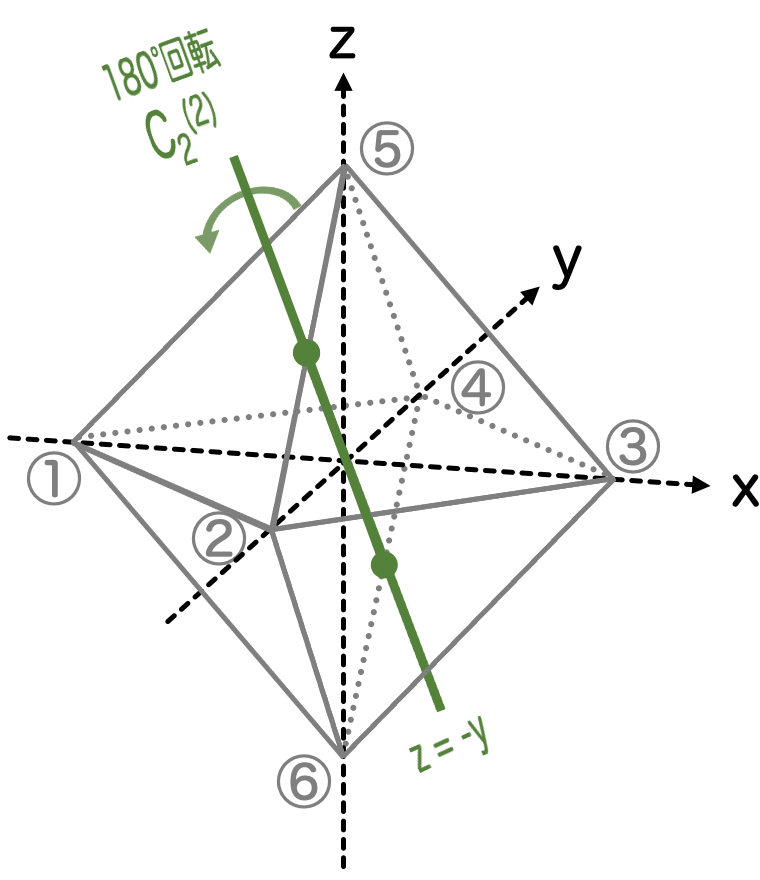
座標 への作用は
となります。
これを3d軌道に作用させるわけですが、 と
が入れ替わるので
の計算が少し大変です。計算のための準備を枠内でしておきましょう。
より
が成り立ちます。
これにより
となりますので、結局
が得られます。
さて、式 を使って
による3d軌道への作用を計算しましょう。
よって
となります。
したがって、 の表現行列が
と求められました。
これまで計算した表現行列をまとめると、次の表が得られます:
今の段階でも、行列が と
の小ブロックになっていそうだと分かりますね。
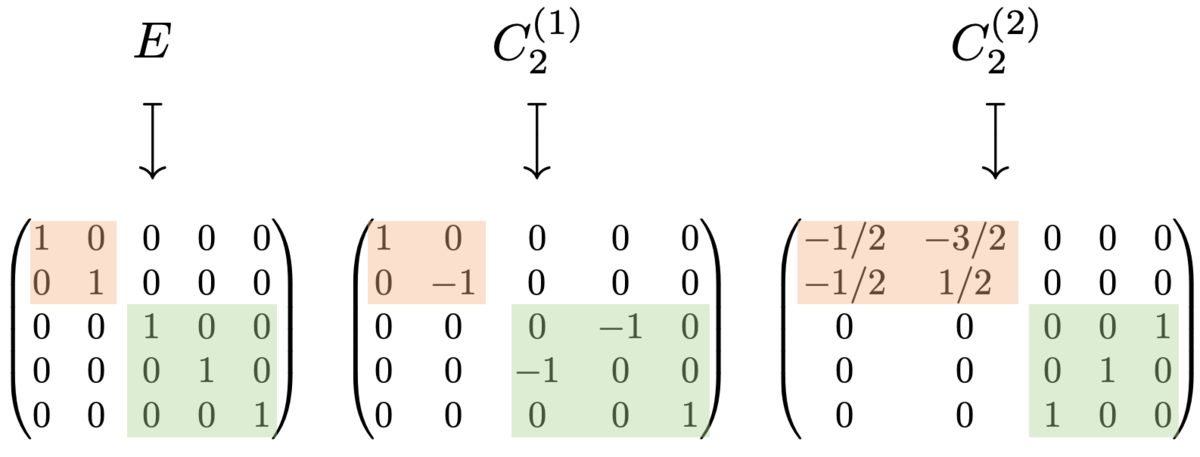
実際、このまま48個の行列を求め続けていけば、 と
の小ブロックに分かれることがわかります。すなわち、可約な表現というわけですね。
小ブロックごとに分離すると、次の式が得られます。
基底 に対する2次元表現と、基底
に対する3次元表現に分けることができました!
これを先ほどの表に反映させるとこうなります:
6. 指標表:表を見れば既約表現がわかる
これにて、3d軌道の基底によって作られる の5次元表現が、2次元表現と3次元表現に分解できたわけですが、これ以上分解はできないのでしょうか?
表現の既約性を簡便に判定する方法として、指標表 を使いたいと思います。
ここでいう指標とは、表現行列の対角成分の和(これをトレースといいます)のことを指します。行列 に対してトレースを
と表します。
これによって という、群の各要素を1次元の値にマッピングする対応が得られたわけですね。
表現 が既約であることは、
が可約であるような基底変換行列
が存在しないことをいうのでした。定義からして、基底変換をすべて考える必要があるので、判定が面倒です。
一方 「指標は基底の取り方によらない」 という性質があります。これは大変ありがたい性質ですね。
がしたがいます。
先ほどの表について、指標を計算するとこうなります:
だいぶすっきりしてきましたね!
ここで、面白いことに気づくのですが、縦の列 と
を比較すると、指標が一致していることがわかります。
共役な要素の集まりを共役類といいます。したがって、共役類のすべての要素は、指標の値が等しくなるというわけです。
そんなわけで、 の列
列はすべて同じ共役類に属するということで、これを
のように表記します。
これを同様に他の共役類に対しても行うと、(もう計算はしませんが)次のような表が得られるそうです。
あとは、この2つの行が既約表現の指標であることが分かればよいわけです。
のすべての既約表現の指標を、上記の要領で並べた表を 指標表 といいます。実は、点群については指標表が分かっているものがあります。(全部わかっているかどうかは私は知りません。)
たとえば、以下のサイトにいけば の指標表がわかります。
ja.webqc.org
上のサイトによれば、 の既約表現は全部で10個あるようです。以下に示します。
| E | 8C2 | 6C2 | 6C4 | 3C2 | i | 6S4 | 8S6 | 3σh | 6σd | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| A2g | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | ||
| Eg | 2 | -1 | 0 | 0 | 2 | 2 | 0 | -1 | 2 | 0 | ||
| T1g | 3 | 0 | -1 | 1 | -1 | 3 | 1 | 0 | -1 | -1 | ||
| T2g | 3 | 0 | 1 | -1 | -1 | 3 | -1 | 0 | -1 | 1 | ||
| A1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| A2u | 1 | 1 | -1 | -1 | 1 | -1 | 1 | -1 | -1 | 1 | ||
| Eu | 2 | -1 | 0 | 0 | 2 | -2 | 0 | 1 | -2 | 0 | ||
| T1u | 3 | 0 | -1 | 1 | -1 | -3 | -1 | 0 | 1 | 1 | ||
| T2u | 3 | 0 | 1 | -1 | -1 | -3 | 1 | 0 | 1 | -1 |
少しだけ表の読み方を補足します。一番左の列は、Mulliken(マリケン)記号 と呼ばれるもので、既約表現についた名称です。
また、一番右側の2列は、表現に対応する波動関数を表したものとなっています。たとえば、 は
を表します。また、
については
なので、これは のことを指しています。
したがって、 や
と書かれた色付きの行が注目すべき行となります。
や
の指標表と、先ほど計算した2次元と3次元の指標表が一致していることを確認しましょう。つまり、この2つの表現は既約表現であったというわけですね。
ところで、この や
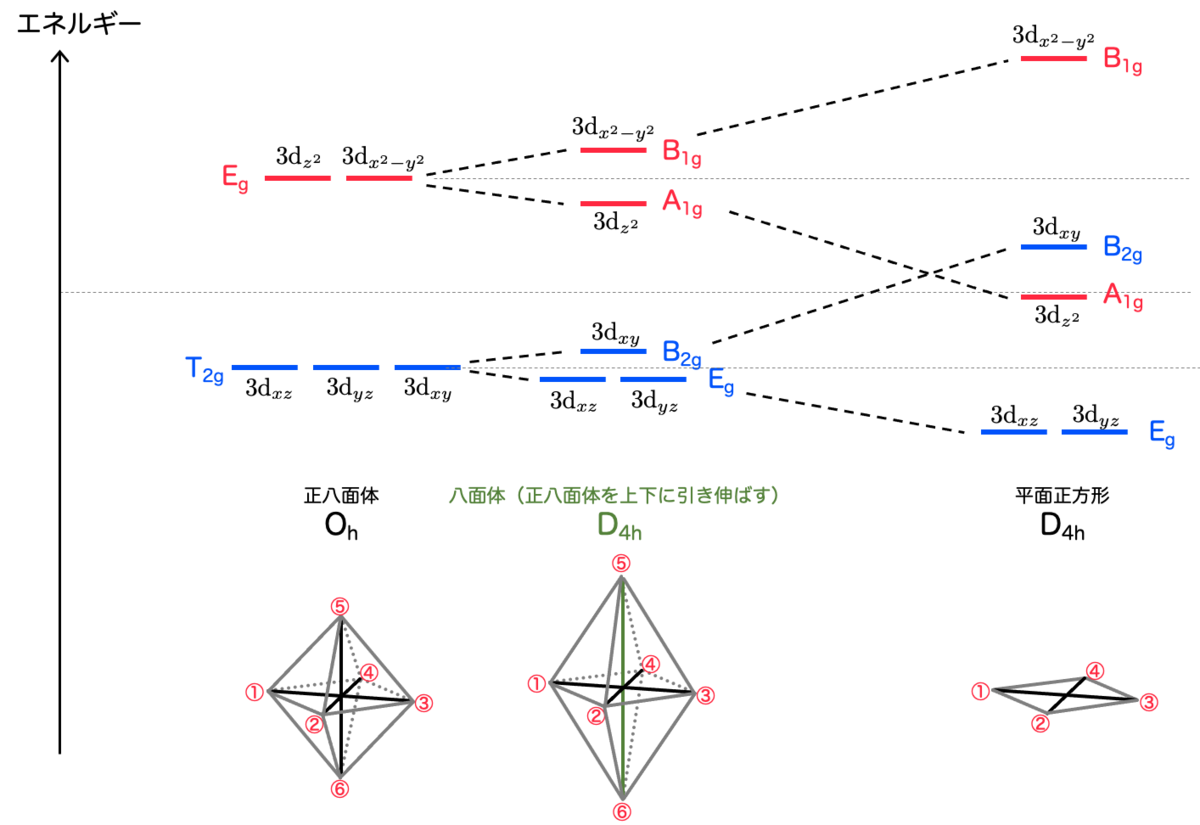
という名前に見覚えはないでしょうか。前回の記事で、3d軌道の縮退が解けたときに、分かれた軌道につけた名前がこれでした。ようやく伏線回収できました。
そんなわけで、我々が計算した2次元表現と3次元表現は既約表現だったということが、指標表から分かりました!
面白いですね!!
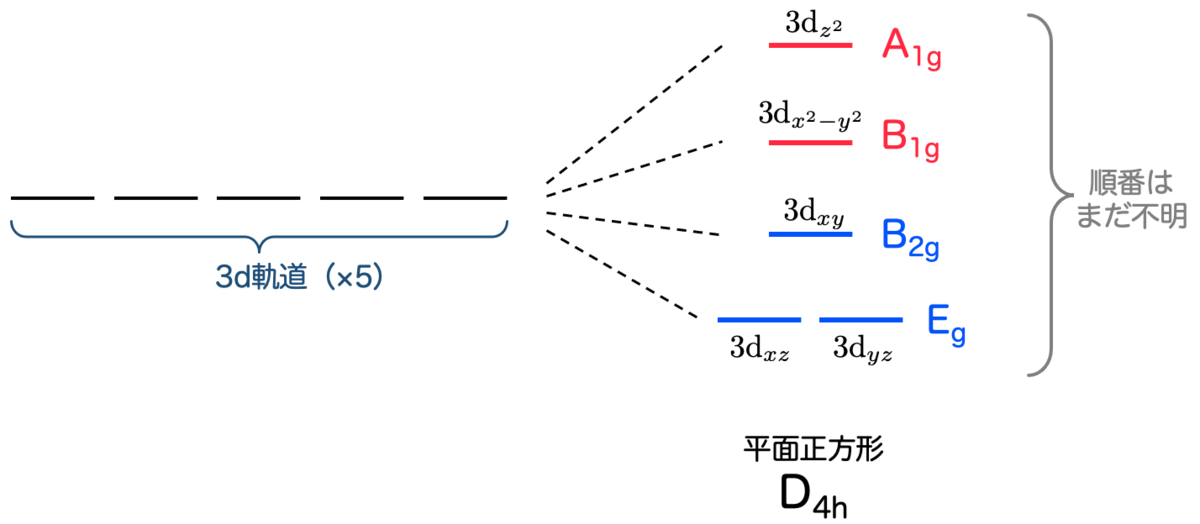
7. 平面正方形の点群 D4h
ここまでは点群が正八面体 の場合について考えてきました。
しかしながら、実際の銅(Ⅱ)錯体の構造は正八面体にはならず、「正八面体を上下に引き伸ばした形」をしていたことを思い出しましょう。この構造に対応する点群は 平面正方形 となります。

そこで、以下では に対する点群
の作用を考え、そこから得られる行列による
の表現を考えます。これを既約表現に分解すれば、縮退する軌道がわかるというわけですね。
で一通りやり方を説明しているので、いきなり指標表(既約表現の指標)を考えたいと思います。
の指標表は以下の通りです:
| E | 2C4(z) | C2 | 2C'2 | 2C''2 | i | 2S4 | σh | 2σv | 2σd | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| A2g | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | ||
| B1g | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | 1 | -1 | ||
| B2g | 1 | -1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | ||
| Eg | 2 | 0 | -2 | 0 | 0 | 2 | 0 | -2 | 0 | 0 | ||
| A1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| A2u | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
| B1u | 1 | -1 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | ||
| B2u | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | ||
| Eu | 2 | 0 | -2 | 0 | 0 | -2 | 0 | 2 | 0 | 0 |
まず、点群 の指標表には5次元の既約表現がないことから、
による5次元表現は可約であるとわかります。既約表現にもっと分解できるというわけです。
この5次元表現は、表の色のついた4行に注目することで、次の4つの既約表現に分解できるとわかります:
(
による1次元表現)
(
による1次元表現)
(
による1次元表現)
(
による2次元表現)
したがって、3d軌道 の縮退は解けていて、
は縮退していることがわかります。3d軌道は
に対応する4つのエネルギーに分かれるわけですね。
正八面体の点群 との関係も考えてみましょう。平面正方形は、正八面体から上下の2頂点を取り除いたものだと思えます。
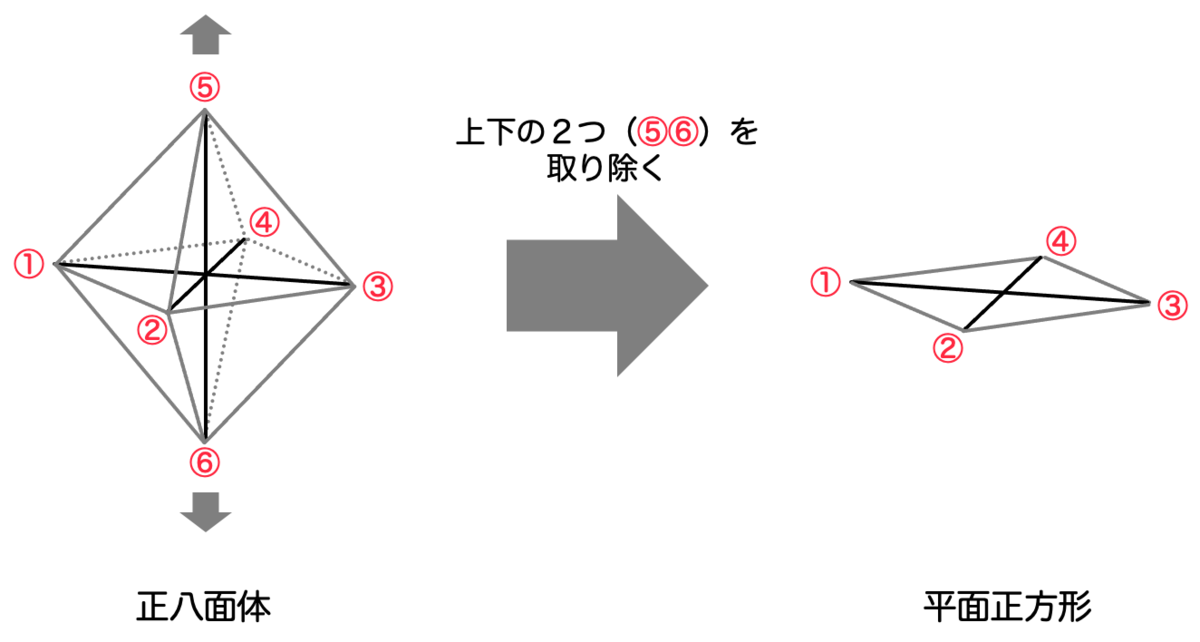
したがって、平面正方形の点群 の要素(16個)は、正八面体の点群
に含まれていることになります。(こういう状況を、群論の言葉で「部分群」といいます。)
この視点で指標表を眺めてみましょう。
の
による表現
は、2次元の既約表現でした。一方で、
の表現としては
による表現は可約です。なぜなら、既約表現のリスト(つまり指標表)に該当するものがないからです。さらに、2つの1次元表現
に分解できます。
また、 の
による表現
は、3次元の既約表現でした。一方で、
の表現としては
による表現は可約です。これは
- 1次元表現
(
による表現)
- 2次元表現
(
による表現)
に分解できます。
以上を図にまとめるとこうなります:
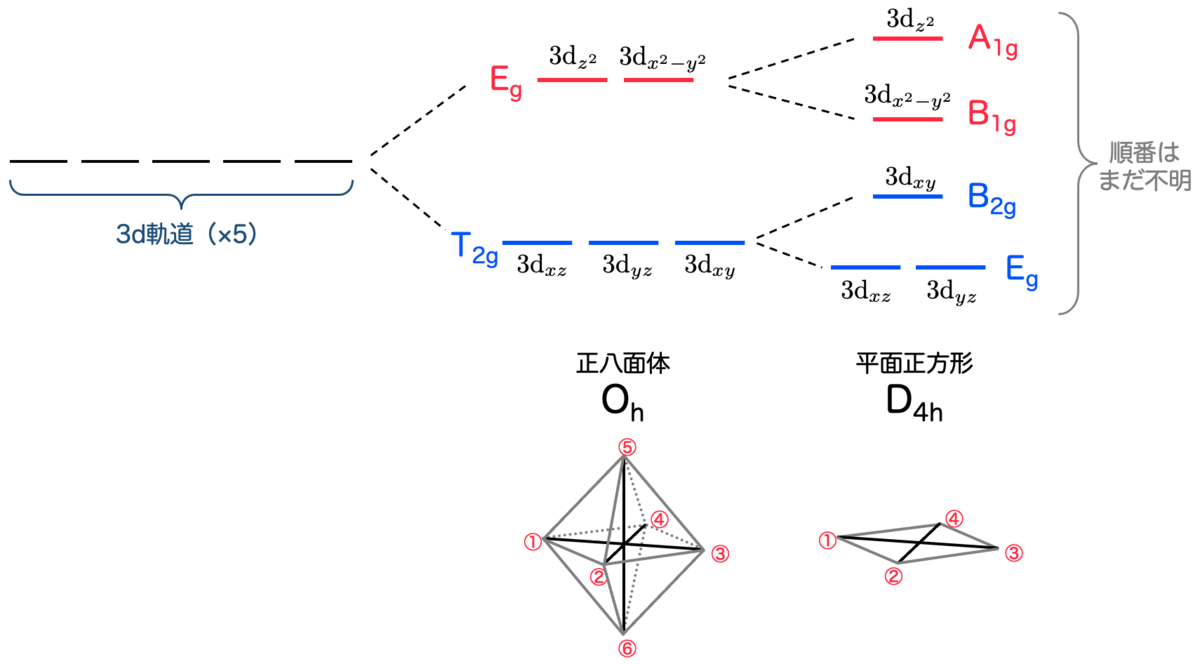
というわけで、分子の対称性が下がることにより縮退が解ける、ということが理解できたかと思います。面白いですね!
ここまでが群論から分かることです。
実際のエネルギーの大小関係については、群論だけでは分かりませんので、具体的に計算する必要があります。
計算結果を参考文献(猪股「錯体化学」)から拝借すると、次のような関係にあるそうです:
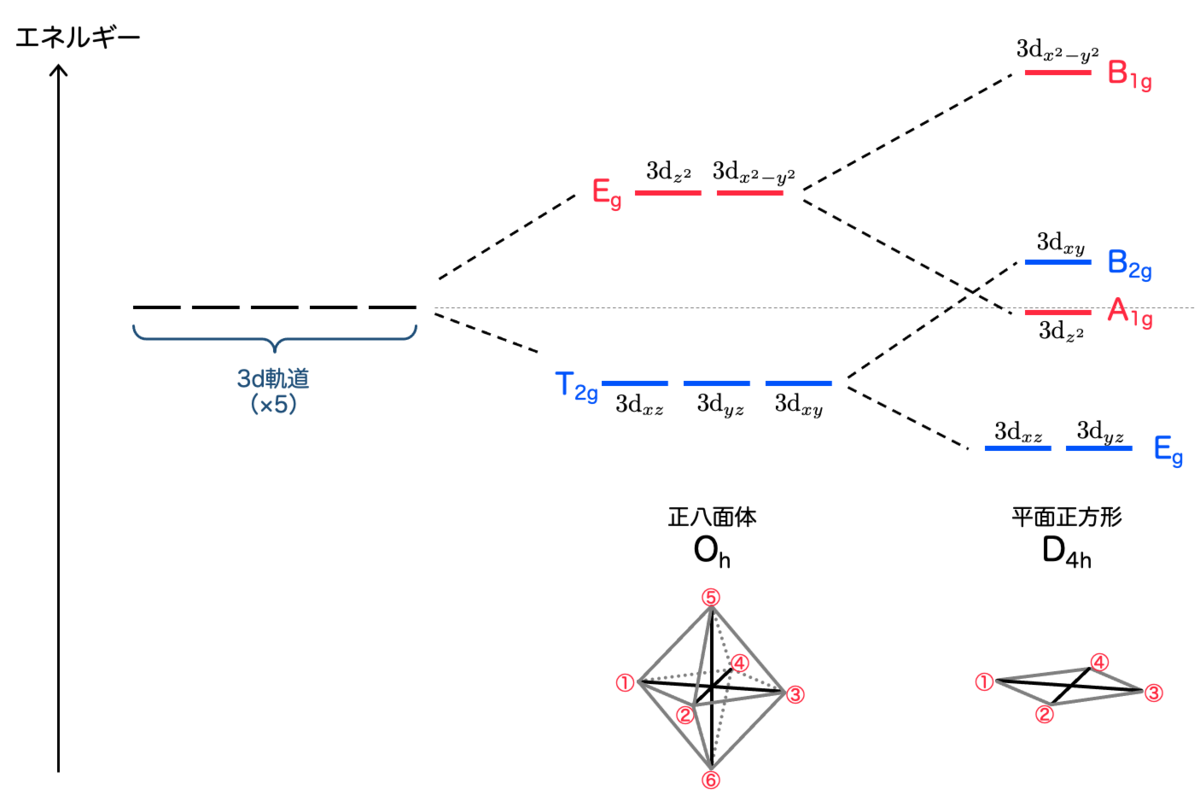
上下2つの頂点を取り除いたことにより、 に対する配位子の影響が小さくなり、かなり安定化していることがわかりますね。逆に、
はかなり不安定化しています。
前回ヤーン・テラー効果を紹介しました。銅錯体は正八面体を上下に引き伸ばした図形になるということでした。
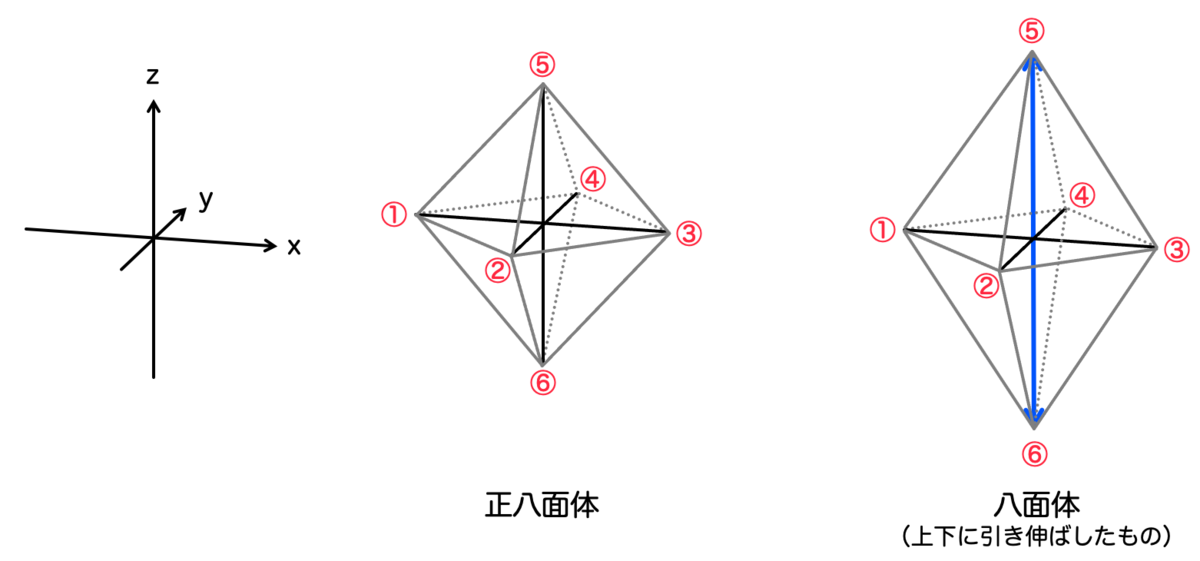
正八面体の頂点⑤⑥を上下に引き伸ばした極限を考えると平面四角形になり、その間くらいの位置に⑤⑥があるので、銅錯体の場合は正八面体と平面四角形のちょうど中間的な性質になりそうです。
この場合、対称性としては なので縮退が解けてエネルギーの個数は4つになります。一方で、正八面体と同様に上下の配位子があるので、
の場合のエネルギーと大きくは変わらない、という具合です。
以上を踏まえて、 と
のちょうど間のような状況を考えると、以下のようなエネルギー図が得られるというわけです:
8. まとめ
結論も得られましたので、元の話に戻って考えましょう。前編と後編の二回にわたって、銅(Ⅱ)イオンの錯体が青色になる仕組みについて考えてきました。少し振り返ってみましょう。
硫酸銅を水に溶かして得られる銅(Ⅱ)イオン や、硫酸銅(Ⅱ)五水和物
の結晶は、銅(Ⅱ)イオンのまわりに八面体状に配位子が置かれた構造をしているのでした。

この八面体は、厳密には正八面体ではなく「正八面体を上下に引き伸ばした図形」となっていました。
中心にある銅イオンにおける5つの3d軌道は、自由空間では縮退していましたが、配位子のクーロン力を受けて縮退が解けます。その解け方は、結晶の対称性によって決まるというのが今日の話でした。
正八面体だと仮定すると、この場合の点群は に対応します。点群
を3d軌道の空間
に作用させると、 の5次元表現が得られます。
問題はこれが可約かどうかで、可約であれば既約な表現に分解する必要がありました。既約な表現に対応する空間はすべて同じエネルギーの固有空間であることがわかり、これによって「縮退がどのように解けるのかがわかる」ということでした。
既約表現のトレースを計算すると指標が得られるわけですが、指標表は既に調べられており、探せば表が見つかります。実際、 の指標表によれば、先の5次元表現は次の既約表現の直和になっていることがわかります:
に対応する2次元表現
に対応する3次元表現
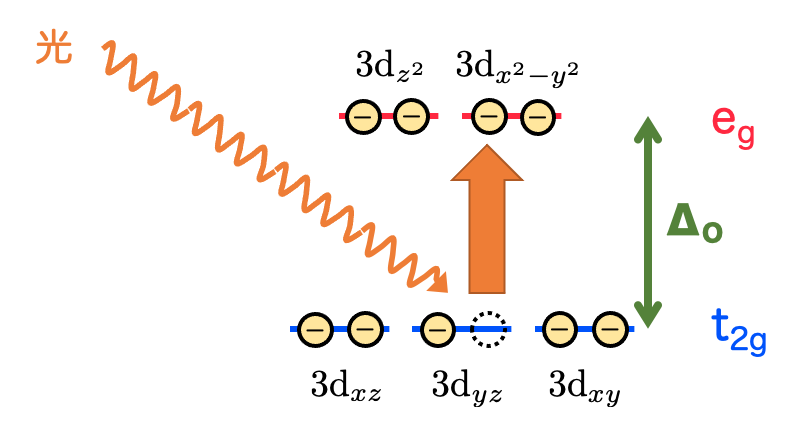
したがって、3d軌道は (2個)と
(3個)に分かれ、このエネルギー差に対応する波長(赤色〜緑色)の光を吸収する。これが硫酸銅の水和物が青い理由である、というわけです!

めでたしめでたし!!
なお、実際の銅イオンは正八面体配位ではありません。対称性としては平面四角形 ということになるわけですが、同様に計算することにより、
が
と
に分かれて、
は、
と
に分かれるということでした。
銅錯体は正八面体と平面四角形の中間的な性質を持つということですね。
いやー、点群ってめっちゃ面白いですね! 今回勉強してみたことで愛着がわき、一気に好きな概念になりました。
特に数学だけを勉強してきた(私のような)人にとっては、群論や表現論がここまで物理・化学に具体的に役にたつというのは、驚くことなのではないでしょうか。
最後まで読んでいただいてありがとうございました! 楽しんでいただけましたでしょうか?
それでは今日はこの辺で!
参考文献
冒頭に書いた通り、今回の記事を書くきっかけとなった記事はこちらです。
http://www.kiriya-chem.co.jp/q&a/q62.htmlwww.kiriya-chem.co.jp
今回の記事の前後編を書くにあたって、以下の教科書を参考にしました。
特に、点群自体の解説(後編)や、点群が結晶場理論にどのように関係するのかという部分(後編)については「分子軌道法」が大変参考になりました。
また、以下は正八面体の対称性を数えるのに参考にしました。



