モジュラー曲線(5)：メイザーの定理 - tsujimotterのノートブック

モジュラー曲線というのは、上半平面 $H$ を $\Gamma = \operatorname{SL(2, \mathbb{Z})}$ の合同部分群で割ったものとして定義されます。

定義からは、明らかに複素解析的な対象に見えると思います。ところが、実はモジュラー曲線は数論的な対象でもあるのです。

わかりやすい応用として、楕円曲線の位数有限な点に関するメイザーの定理があります。

定理（メイザーの定理）

$E$ を $\mathbb{Q}$ 上の楕円曲線とする。このとき、 $E$ の位数有限の有理点の位数 $N$ は、 $N = 1,2,3,4,5,6,7,8,9,10,12$ のいずれかである。

これは楕円曲線の有理点の構造を決定するために大変有用な定理です。数論における大定理といってよいと思うのですが、この定理を証明するのにモジュラー曲線が用いられるのです。

メイザーの定理の証明自体は私は理解できていないので、ここでは解説はできません。今回は、位数有限の有理点とモジュラー曲線の関係に限って紹介したいという記事です。

話のキーとなるのは、モジュラー曲線の一点一点が楕円曲線の同型類に対応するという事実です。つまり、モジュラー曲線は楕円曲線のモジュライ空間であるのです。

また、モジュラー曲線のもう一つの側面として、代数曲線としての性質があります。具体的に、方程式のなす点集合として表すことができるのです。この曲線としての性質から、たとえば位数Nの有理点を持つ楕円曲線が存在しないことが言えてしまうのです。

そんなわけでモジュラー曲線のすごさをお伝えしたいと思います。

今回の記事はtsujimotterがまさに勉強中の「理解の最前線」を書いている記事となっています。私の理解不足により誤りを含んでいる可能性があります。
勉強する際は、私の記述をうのみにせず参考文献をご参照いただければと思います。参考文献は一番下に書いています。

また「モジュラー曲線」シリーズの過去記事はこちらで読むことができます：
tsujimotter.hatenablog.com

今回の記事はシリーズ記事ですが、前回（モジュラー曲線(4)）からずいぶんと時間が経ってしまいましたので、この記事単体で読めるような記事にしたいと思います。そのため、過去の記事と重複する部分もかなりあるかと思います。必要に応じて過去の記事を参照してみてください。

合同部分群とモジュラー曲線のおさらい

このブログでも何度かモジュラー曲線について解説していますが、話の内容に必要な部分をさらっとおさらいしたいと思います。

詳しくは、たとえば下記の記事をご覧ください：
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

まず、冒頭で述べたように $\Gamma = \operatorname{SL}(2, \mathbb{Z})$ とします。 $\Gamma$ の部分群として、 $\Gamma_0(N), \Gamma_1(N), \Gamma(N)$ を次のように定義したいと思います：

$\Gamma_0(N) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma \; \middle| \; \begin{pmatrix} a & b \\ c & d \end{pmatrix} \equiv \begin{pmatrix} * & * \\ 0 & * \end{pmatrix} \pmod{N} \right\}$

$\Gamma_1(N) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma \; \middle| \; \begin{pmatrix} a & b \\ c & d \end{pmatrix} \equiv \begin{pmatrix} * & * \\ 0 & 1 \end{pmatrix} \pmod{N} \right\}$

$\Gamma(N) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma \; \middle| \; \begin{pmatrix} a & b \\ c & d \end{pmatrix} \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \pmod{N} \right\}$

これらをレベル $N$ の合同部分群といいます。

$\displaystyle \Gamma(N) \subset \Gamma_1(N) \subset \Gamma_0(N) \subset \Gamma$

の関係があります。今回主に使うのは $\Gamma_1(N)$ となります。

ここで、 $\Gamma'$ を $\Gamma, \Gamma_0(N), \Gamma_1(N), \Gamma(N)$ のいずれかとし、上半平面を

$H := \{\tau \in \mathbb{C} \mid \operatorname{Im}(\tau) > 0 \}$

とます。 $H$ の点 $\tau$ に対して、 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ の作用を次のように定義します：

$\displaystyle \gamma \tau := \frac{a\tau + b}{c\tau + d}$

この作用を用いて、 $H$ の点 $\tau, \tau'$ に対して、次の同値関係を入れます：

$\tau \sim \tau \;\; \Longleftrightarrow \;\;$ ある $\gamma \in \Gamma'$ が存在して $\tau = \gamma \tau'$

このような同値関係で割って得られる商集合を $\Gamma' \setminus H$ と表し、 $\Gamma'$ についてのモジュラー曲線ということにします。

モジュラー曲線には、 $\mathbb{C}$ から誘導される位相によって位相空間だと思えるのですが、この位相について連結な代表元のなす集合を $\Gamma'$ についての基本領域と言います。

たとえば、 $\Gamma$ についてのモジュラー曲線 $\Gamma \setminus H$ は、次のような基本領域をとることができます：

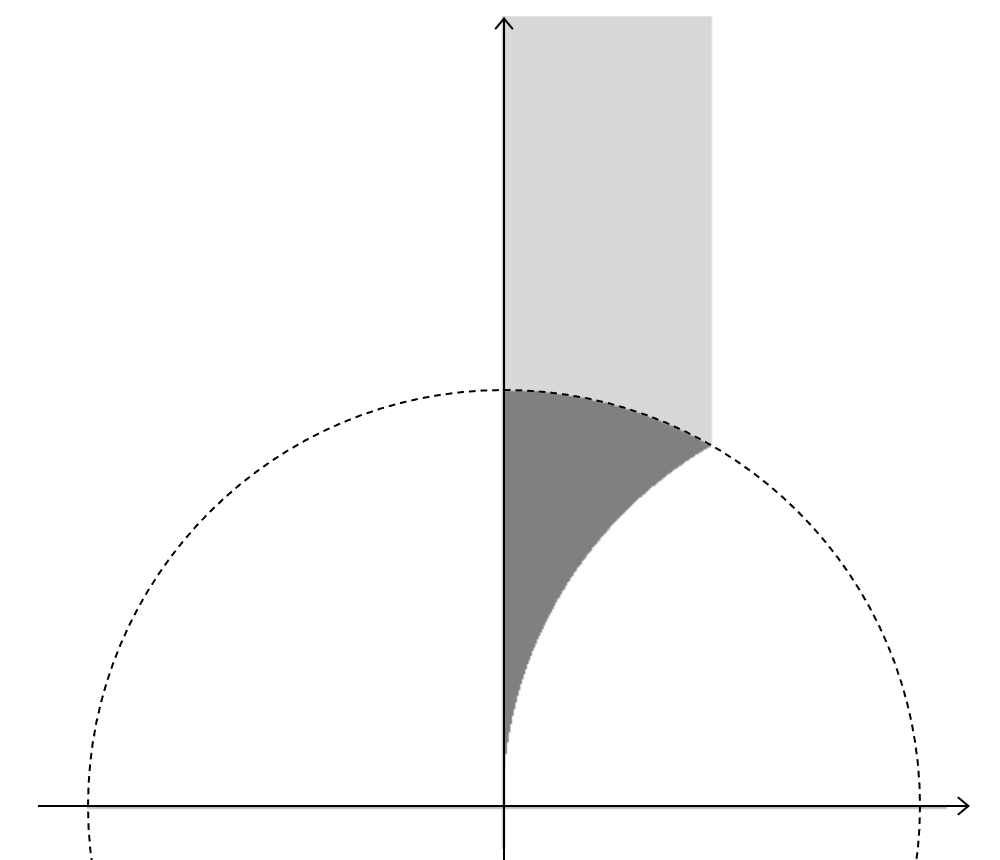
f:id:tsujimotter:20210501000332p:plain:w300

ほかにも、 $\Gamma_1(11)\setminus H$ の基本領域を描画すると、次のようになります：

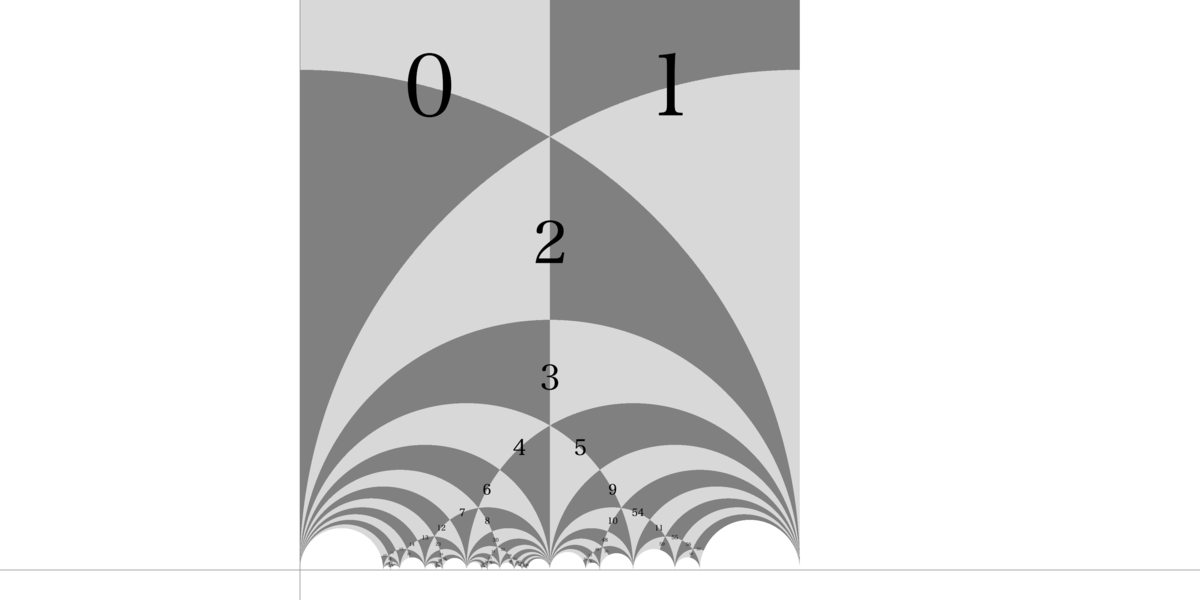
これは $\Gamma$ についての基本領域を考えて、これを60枚コピーしてタイリングしたものになっています。 $\Gamma / \Gamma_1(11)$ の適当な代表元によって、 $\Gamma$ についての基本領域を写すことによって得られます。

この $\Gamma_1(11)$ についてのモジュラー曲線は、今回の記事の中で何度も登場することになります。

さらっと書いていますが、今回この図を作るのが一番大変でした。基本領域の各パートに対応する行列を決定するために新たにツールを開発したりしました。

上記のモジュラー曲線は、単に位相空間であるばかりか、適当なアトラスを入れることでリーマン面の構造を持ちます。しかし、コンパクトではないので、コンパクト化するために、次のように考えることが多いです。

拡張された上半平面 $H^* = H \cup \{i\infty\} \cup \mathbb{Q}$ を考えます。これを $\Gamma' = \Gamma, \Gamma_0(N), \Gamma_1(N), \Gamma(N)$ で割って得られる空間を $\Gamma' \setminus H^*$ と表しますが、これも $\Gamma'$ についてのモジュラー曲線ということにします。

$\Gamma' \setminus H^* - \Gamma' \setminus H$ 内の点をカスプといいます。 $i\infty$ や $\mathbb{Q}$ の点に対応する同値類がカスプに対応するわけです。これによって、コンパクトな位相空間となるわけですね。

さらにリーマン面の構造も持つことが知られています。よって、 $\Gamma' \setminus H^*$ はコンパクトリーマン面ということになります。

$\Gamma$ についてのモジュラー曲線 $\Gamma \setminus H^*$ は、 $X(1)$ のように表しますが、1点 $[i\infty]$ をカスプに持ちます。こういうのを1点コンパクト化と言ったりしますね。

また、 $\Gamma_1(N)$ についてのモジュラー曲線 $\Gamma_1(N) \setminus H^*$ を $X_1(N)$ のように表すことにします。 $X_1(N)$ のカスプは、 $[i\infty]$ のみとは限らず、たとえば $X_1(11)$ は次の10点のカスプを持ちます。

$\{ [0], \; [1/6], \; [2/11], \; [1/4], \; [3/11], \; [1/3], \; [4/11], \; [4/9], \; [5/11], \; [i\infty] \; \}$

楕円曲線のモジュライとしてのモジュラー曲線

モジュラー曲線上の一点一点には楕円曲線の同型類が対応する（楕円曲線のモジュライである）ということについて、ここでは解説したいと思います。

より詳しくは過去の記事で解説しています。
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

まず、楕円曲線から復習したいと思います。

楕円曲線とは、種数1の非特異射影代数曲線のことですが、 $\mathbb{C}$ 上の楕円曲線は

$y^2 = x^3 + ax + b$

の形（ $a, b\in \mathbb{C}, \; 4a^3+27b^2 \neq 0$ ）で表せることが知られています。

一方、 $\tau$ を上半平面上にとって、 $\{1, \tau\}$ で張られる $\mathbb{C}$ の格子を $\Lambda_{\tau} = \mathbb{Z} + \tau\mathbb{Z}$ とします。 $\mathbb{C}/\Lambda_\tau$ は、ベクトル $1, \tau$ によって表される平行四辺形状の領域を基本領域に持ちますが、これはリーマン面としてはトーラスに対応します。

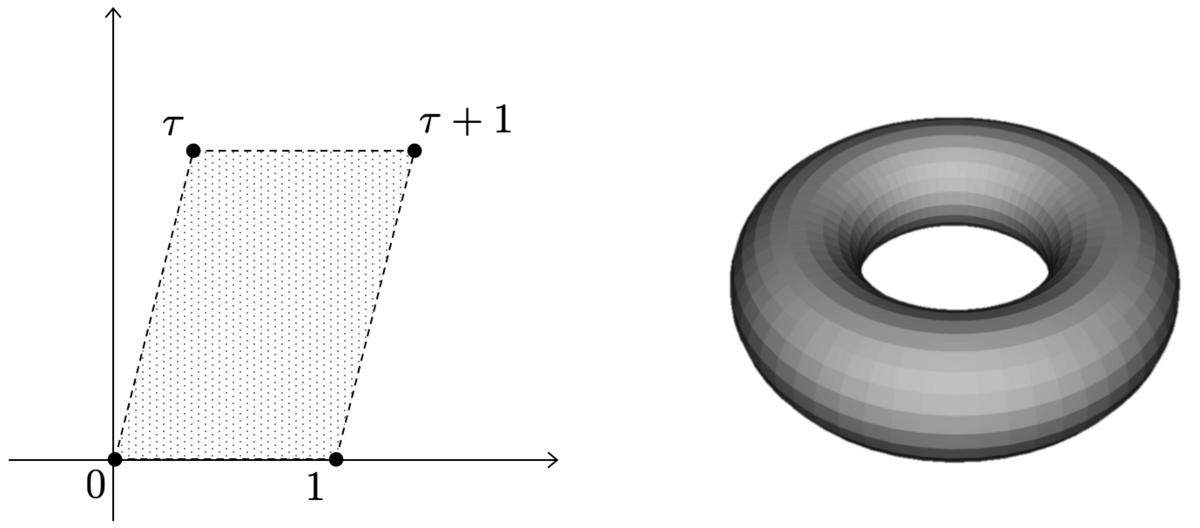
f:id:tsujimotter:20210501100306p:plain:w360

格子 $\Lambda_\tau$ に対するワイエルシュトラスのペー関数 $\wp(z; \Lambda_\tau)$ とその微分 $\wp'(z; \Lambda_\tau)$ を通して、 $\mathbb{C}/\Lambda_{\tau}$ は楕円曲線に対応します。これを $E_{\tau}$ で表すことにします。

$\displaystyle \begin{align} [\wp : \wp' : 1]\;\colon \;\mathbb{C}/\Lambda_{\tau} \;\; &\longrightarrow \;\;E_{\tau} \;\; (\subset \mathbb{P}^2), \\ [z] \;\;\;\; &\longmapsto \; [\wp(z) : \wp(z)': 1] \end{align}$

なお、上記で $[0]$ に対応する点 $O = [0 : 1 : 0]$ を楕円曲線 $E_{\tau}$ の無限遠点といいます。

以降、上記の写像を通して、トーラス $\mathbb{C}/\Lambda_{\tau}$ と楕円曲線 $E_{\tau}$ を同一視します。

楕円曲線 $E, E'$ の間の正則写像 $\phi\colon E \to E'$ であって、 $\phi(O) = O'$ であるものを同種写像といいます。同種写像は $\mathbb{C}$ 上の楕円曲線全体のなす圏における射となります。同種写像はトーラス上では $\alpha \in \mathbb{C}^\times$ 倍写像 $\phi(z) = \alpha z$ に対応します。このとき、格子では $\alpha \Lambda \subset \Lambda'$ が成り立つことになります。

逆向きの同種写像 $\phi\colon E \to E'$ と $\psi\colon E' \to E$ があり、 $\psi\circ \phi = \operatorname{id}_{E}, \; \phi\circ \psi = \operatorname{id}_{E'}$ が成り立つとき、 $\phi$ は同型射であるといいます。このとき、 $E$ と $E'$ は同型であるといい、 $E \simeq E'$ と表します。

$E \simeq E'$ のとき、格子においてはちょうど $\alpha \Lambda = \Lambda'$ が成り立つことになります。楕円曲線 $E$ 、トーラス $\mathbb{C}/\Lambda$ 、格子 $\Lambda$ がそれぞれパラレルに話が進んでいくことになります。

さて、 $\Gamma \setminus H$ の各点 $[\tau]$ には、楕円曲線の同型類 $[E_{\tau}]$ が対応するという話をしましょう。

まず次の定理が成り立ちます：

定理2

$\tau, \tau' \in H$ とする。このとき、次は同値：

ある $\gamma \in \Gamma$ が存在して $\tau = \gamma \tau'$
ある $\alpha \in \mathbb{C}^\times$ が存在して、 $\phi\colon E_{\tau} \to E_{\tau'}, \phi(z) = \alpha z$ は楕円曲線の同型射

この定理の証明を簡単に述べたいと思います。

ある $\gamma \in \Gamma$ が存在して $\tau = \gamma \tau'$ が成り立つということから話をはじめます。 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ としておきます。

$\tau = \frac{a\tau' + b}{c\tau' + d}$ が成り立つので、 $\alpha = c\tau' + d$ とおくと $\alpha \tau = a\tau' + b$ が成り立ちます。すなわち

$\displaystyle \begin{pmatrix} \alpha\tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

ということです。これは格子 $\alpha\Lambda_{\tau}$ の基底 $\{\alpha \tau, \alpha\}$ が、 $\Lambda_{\tau'}$ の基底 $\{\tau', 1\}$ の基底変換によって移ることを表しており

$\alpha \Lambda_{\tau} = \Lambda_{\tau'}$

が言えます。したがって、楕円曲線の間の同型射

$\phi\colon E_{\tau} \longrightarrow E_{\tau'}$

であって、 $\phi(z) = \alpha z$ であるものが得られるというわけです。

逆に、楕円曲線の間の同型射

$\phi\colon E_{\tau} \longrightarrow E_{\tau'}$

であって、 $\phi(z) = \alpha z$ であるものがあるとすると、 $\alpha \Lambda_{\tau} = \Lambda_{\tau'}$ が成り立ち、基底変換行列を

$\displaystyle \begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

で表すと、 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ が $\gamma \in \Gamma$ であることがわかり、

$\displaystyle \tau = \frac{\alpha \tau}{\alpha} = \frac{a\tau' + b}{c\tau' + d} = \gamma \tau'$

が得られるという寸法です。

したがって、 $\Gamma\setminus H$ の各点 $[\tau]$ に楕円曲線の同型類 $[E_\tau]$ を対応させる写像は全単射となります。すなわち、 $\Gamma\setminus H$ は楕円曲線のモジュライ空間ということになるわけです。

より細かい分類：拡張された楕円曲線の同型類と $\Gamma_1(N)\setminus H$

楕円曲線のモジュライ空間として $\Gamma\setminus H$ を考えましたが、楕円曲線の同型というのは比較的緩い条件です。もう少し細かく分類したいというのが次の話です。

特に、先ほどまではすべての楕円曲線を考えましたが、今度は正の整数 $N$ に対して「位数 $N$ の点を持つ楕円曲線だけ」を対象としたいと思います。

このような楕円曲線 $E$ に対して位数 $N$ の点を１つ選んで $P$ とし、組 $(E, P)$ を考えます。これを拡張された楕円曲線ということにします。

以前の記事では「レベル構造付き楕円曲線」と呼んでいたものです。今回呼び方を変えていますが、全く同じものです。）
tsujimotter.hatenablog.com

拡張された楕円曲線においては、たとえば $E$ が同じであっても、 $P \neq Q$ であれば $(E, P) \neq (E, Q)$ であると考えます。

拡張された楕円曲線 $(E, P), (E', P')$ の間の射を次の２つの条件で定義します：

$\phi\colon E \longrightarrow E'$ は楕円曲線の同種写像
$\phi(P) = P'$

つまり、単に同種写像であるだけでなく、 $P$ が $P'$ に映されるという条件も課されるわけですね。

これによって、楕円曲線の同型射と同じように拡張された楕円曲線に対しても同型射が定義されます。このような同型射によって、 $(E, P)$ の同型類 $[E, P]$ が定義されます。同型類 $[E, P]$ 全体の集合を $S_1(N)$ と表すことにしましょう。

実は、カスプを除いたモジュラー曲線 $\Gamma_1(N)\setminus H$ と $S_1(N)$ の間には全単射が存在するのです。これを示しましょう。

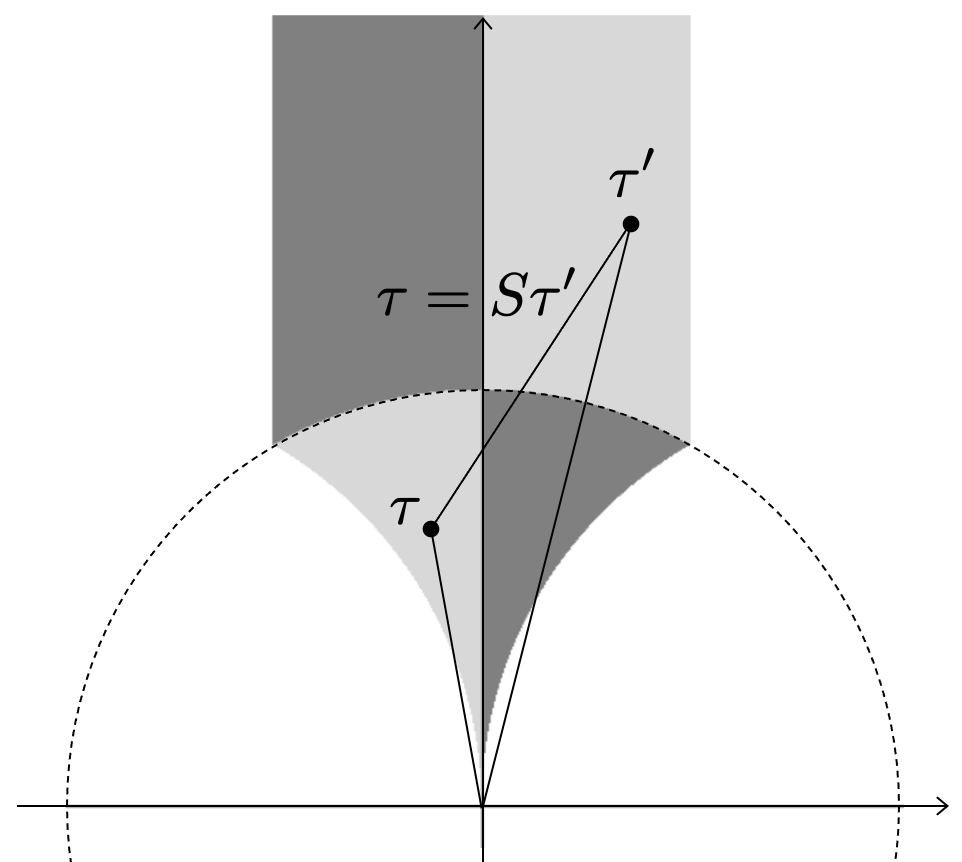
まず、 $\tau, \tau'$ を上半平面上の点とし、対応する楕円曲線をそれぞれ $E_{\tau}, E_{\tau'}$ とします。また、 $E_{\tau}$ の位数 $N$ の点を $P_{\tau} = \frac{1}{N}\bmod{\Lambda_{\tau}}$ とし、同じく $E_{\tau'}$ の位数 $N$ の点を $P_{\tau'} = \frac{1}{N}\bmod{\Lambda_{\tau'}}$ とします。位置は図の通りですが、 $N$ 倍したら $0\bmod{\Lambda_{\tau}}$ （ $0\bmod{\Lambda_{\tau'}}$ ）になることに注意しましょう。

f:id:tsujimotter:20210501095745p:plain:w400

今、 $\tau, \tau' \in H$ に対してある $\gamma \in \Gamma$ が存在して $\tau = \gamma \tau'$ が成り立つとします。
（今はまだ $\Gamma = \operatorname{SL}(2, \mathbb{Z})$ であることに注意。）

このとき、 $\gamma \in \Gamma$ より $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ と表せます。ここで、先ほどと同様に $\alpha = c\tau' + d$ とおくと、 $\alpha \Lambda_{\tau} = \Lambda_{\tau'}$ が成り立ち、楕円曲線の同型射 $\phi\colon E_{\tau}\longrightarrow E_{\tau'}, \;\; \phi(z) = \alpha z$ が得られます。

さらに、 $P_\tau = 1/N\bmod{\Lambda_{\tau}}$ を $\phi$ で写すことを考えましょう。計算すると

$\displaystyle \begin{align} \phi(P_{\tau}) &= \phi(\frac{1}{N}\bmod{\Lambda_{\tau}}) \\ &= \frac{\alpha}{N}\bmod{\Lambda_{\tau'}} \\ &= \frac{c\tau' + d}{N}\bmod{\Lambda_{\tau'}} \end{align}$

となります。

ここでもし、 $\gamma \in \Gamma_1(N)$ だったとしましょう。すると、 $c\equiv 0, \; d \equiv 1\pmod{N}$ となりますので

$\displaystyle \begin{align} \phi(P_{\tau}) &= \frac{c\tau' + d}{N}\bmod{\Lambda_{\tau'}} \\ &= \frac{1}{N}\bmod{\Lambda_{\tau'}} \end{align}$

が成立します。 $\phi(P_{\tau}) = P_{\tau'}$ が成り立つということですね。 $\phi\colon (E_{\tau}, P_{\tau}) \longrightarrow (E_{\tau'}, P_{\tau'})$ は拡張された楕円曲線における同型射であるということを意味します。

逆に、楕円曲線の間の同型射

$\phi\colon E_{\tau} \to E_{\tau'}, \; \phi(z) = \alpha z, \; \phi(P_{\tau}) = P_{\tau'}$

が与えられたときに、整数 $a, b, c, d$ を用いて基底変換

$\displaystyle \begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

が得られます。変換行列を $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ とおきます。

ここでもし

$\phi(P_{\tau}) = P_{\tau'}$

が成り立つのであれば（拡張された楕円曲線の間の同型射であれば）、 $\gamma \in \Gamma_1(N)$ であることが容易に示せます。

したがって、次の定理が成り立つというわけですね：

定理3

$\tau, \tau' \in H$ とし、 $P_\tau = 1/N\bmod{\Lambda_\tau}, P_{\tau'} = 1/N\bmod{\Lambda_{\tau'}}$ とする。このとき、次は同値：

ある $\gamma \in \Gamma_1(N)$ が存在して $\tau = \gamma \tau'$
ある $\alpha \in \mathbb{C}^\times$ が存在して、 $\phi\colon E_{\tau} \to E_{\tau'}, \phi(z) = \alpha z, \phi(P_{\tau}) = P_{\tau'}$ は、拡張された楕円曲線の同型射

これによって、 $\Gamma_1(N)\setminus H$ の各点 $[\tau]$ に拡張された楕円曲線の同型類 $[E_\tau, P_{\tau}]$ を対応させる写像は全単射となります。

$\begin{align} \Gamma_1(N)\setminus H \;\;&\longleftrightarrow \;\; S_1(N) \\ [\tau] \;\; &\longmapsto \; [E_\tau, P_{\tau}] \end{align}$

具体的に２つの楕円曲線を考えて、これらが拡張された楕円曲線として同型であるかどうかを確認してみましょう。 $N = 11$ として $\Gamma_1(11)$ を考えたいと思います。

$\tau, \tau' \in H$ を次の図のように取りましょう。

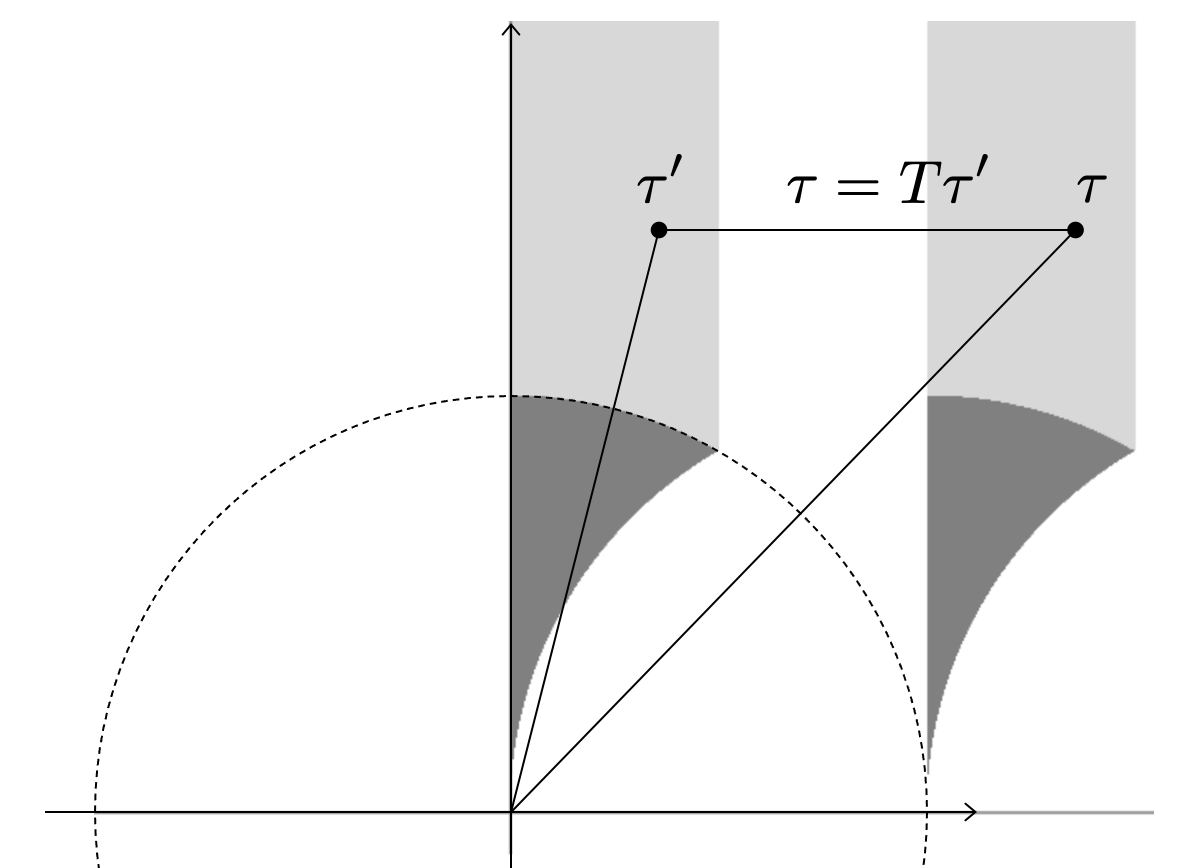
f:id:tsujimotter:20210501093657p:plain:w300

これらは $\tau = \tau'+1$ の関係があります。すなわち $T = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$ として、 $\tau = T \tau'$ ということです。

ここで、 $T \in \Gamma$ であり、もっというと $T \in \Gamma_1(11)$ でもあります。

$\alpha = 0\cdot \tau + 1 = 1$ なので

$\displaystyle 1\cdot \Lambda_{\tau} = \Lambda_{\tau'}$

となります。つまり、トーラスとして同型 $\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$ ということになります。
（この場合は格子の時点で等しいので、単に同型であるばかりか、トーラスとして一致します。）

したがって、楕円曲線としての同型射 $\phi\colon E_{\tau} \simeq E_{\tau'}, \phi(z) = \alpha z$ が得られます（ $\alpha = 1$ ）。

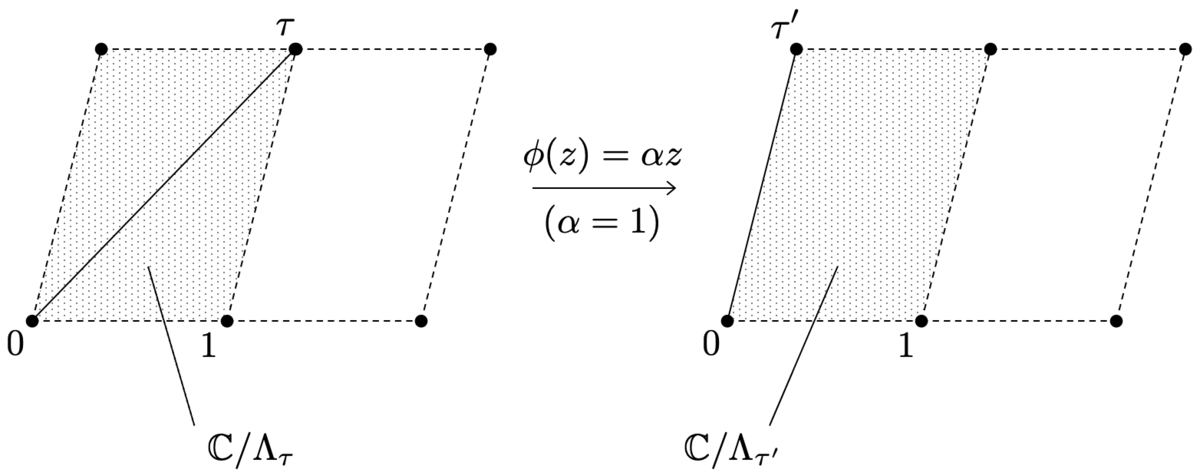
f:id:tsujimotter:20210501093853p:plain:w480

$P_{\tau} = 1/11\bmod{\Lambda_{\tau}}, \; P_{\tau'} = 1/11\bmod{\Lambda_{\tau'}}$ として、拡張された楕円曲線 $(E_{\tau}, P_{\tau}), (E_{\tau'}, P_{\tau'})$ を考えます。これらが拡張された楕円曲線として同型であることを示します。

先ほどの $\phi$ を $P_{\tau}$ に適用すると

$\displaystyle \begin{align} \phi(P_{\tau}) &= \frac{0\cdot \tau' + 1}{11}\bmod{\Lambda_{\tau'}} \\ &= \frac{1}{11}\bmod{\Lambda_{\tau'}} \\ &= P_{\tau'} \end{align}$

となります。すなわち、 $\phi(P_{\tau}) = P_{\tau'}$ なので、 $\phi\colon (E_{\tau}, P_{\tau}) \longrightarrow (E_{\tau'}, P_{\tau'})$ は拡張された楕円曲線としての同型射です。

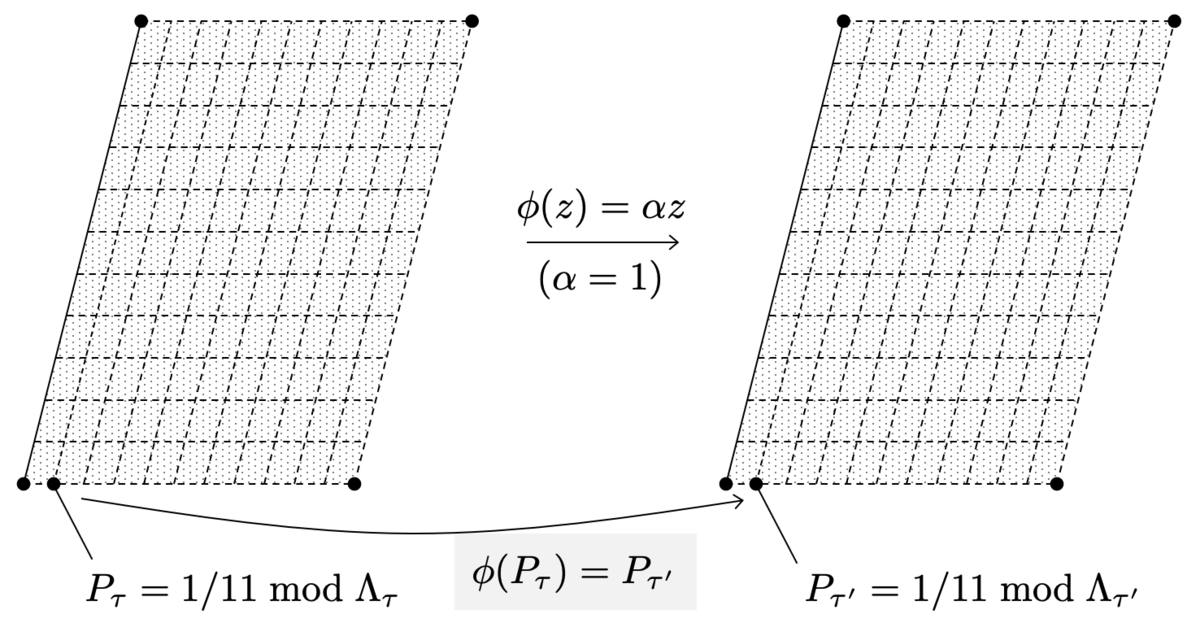
f:id:tsujimotter:20210501093936p:plain:w400

続いて、 $S = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ として、 $\tau = S\tau'$ となるような $\tau, \tau' \in H$ を考えましょう。

f:id:tsujimotter:20210501094046p:plain:w300

$S \in \Gamma$ ではあるが、 $S \not\in \Gamma_1(11)$ であるという例を考えています。

$\alpha = 1\cdot \tau' + 0 = \tau'$ なので

$\displaystyle \tau'\cdot \Lambda_{\tau} = \Lambda_{\tau'}$

となります。つまり、トーラスとして同型 $\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$ であり、楕円曲線における同型射 $\phi\colon E_{\tau} \simeq E_{\tau'}, \phi(z) = \alpha z$ が得られます（ $\alpha = \tau'$ ）。

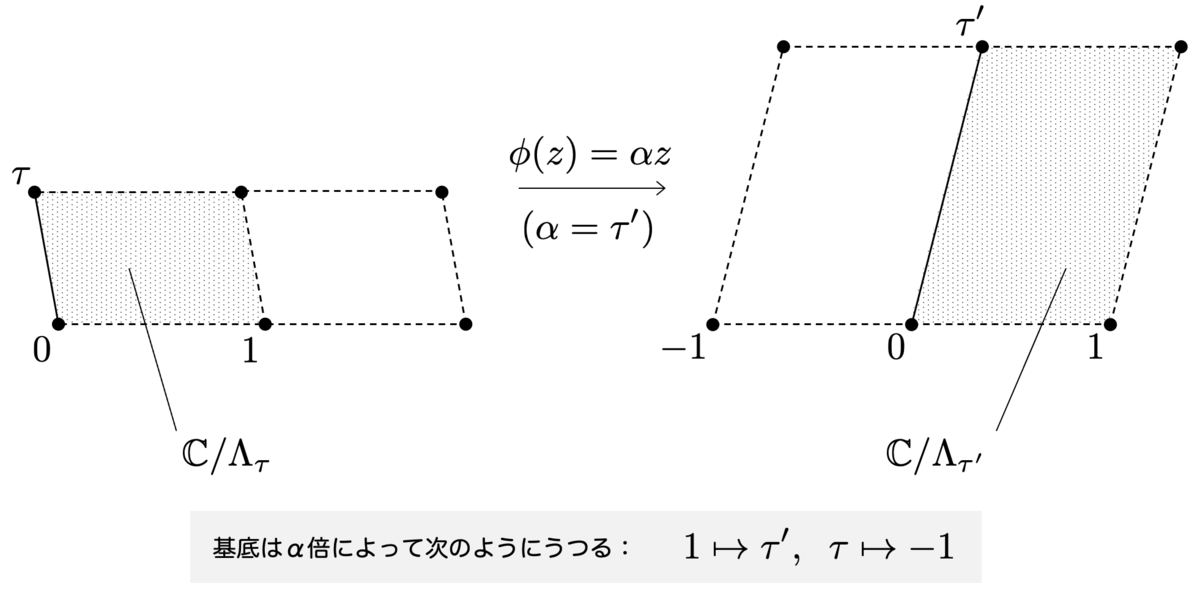
f:id:tsujimotter:20210501141701p:plain:w480

ここで、 $P_{\tau} = 1/11\bmod{\Lambda_{\tau}}, \; P_{\tau'} = 1/11\bmod{\Lambda_{\tau'}}$ として、拡張された楕円曲線 $(E_{\tau}, P_{\tau}), (E_{\tau'}, P_{\tau'})$ を考えます。

先ほどの $\phi$ を $P_{\tau}$ に適用すると

$\displaystyle \begin{align} \phi(P_{\tau}) &= \frac{1\cdot \tau' + 0}{11}\bmod{\Lambda_{\tau'}} \\ &= \frac{\tau'}{11}\bmod{\Lambda_{\tau'}} \\ &\neq P_{\tau'} \end{align}$

となります。すなわち、 $\phi(P_{\tau}) \neq P_{\tau'}$ なので、 $\phi\colon (E_{\tau}, P_{\tau}) \longrightarrow (E_{\tau'}, P_{\tau'})$ は拡張された楕円曲線としての同型射ではありません。

一方、 $(E_{\tau}, 1/11\bmod{\Lambda_{\tau}})$ と $(E_{\tau'}, \tau'/11\bmod{\Lambda_{\tau'}})$ は同型となります。

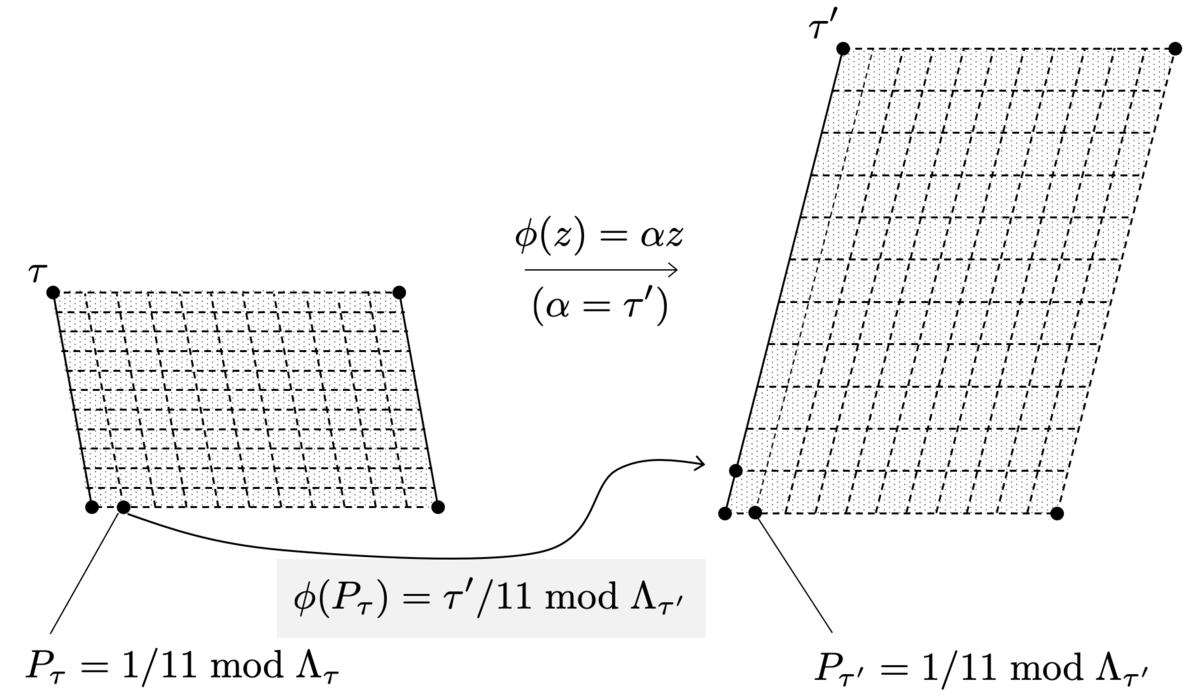
f:id:tsujimotter:20210501141724p:plain:w480

今の $S$ のように、 $\gamma \in \Gamma$ ではあるが $\gamma \not\in \Gamma_1(11)$ であるような元（すなわち $\Gamma - \Gamma_1(11)$ の元）は、 $E_{\tau} \simeq E_{\tau'}$ でありつつも、 $(E_{\tau}, 1/11\bmod{\Lambda_{\tau}}) \not\simeq (E_{\tau}, 1/11\bmod{\Lambda_{\tau'}})$ であるということです。

実際、楕円曲線の同型射 $\phi\colon E_{\tau} \to E_{\tau'}, \; \phi(z) = (c\tau' + d)z$ によって、 $1/11\bmod{\Lambda_{\tau}}$ は $\frac{c\tau'+d}{11}\bmod{\Lambda_{\tau'}}$ に映されてしまうわけですね。

結局、 $\Gamma\setminus H$ の基本領域 $\Omega$ 内の点にとったときに、 $1/11\bmod{\Lambda_\tau} \in E_{\tau}$ が $\gamma \in \Gamma/\Gamma_1(11)$ によってどこに映されるかが、 $\gamma\Omega$ の位置関係とちょうど対応することになります。

f:id:tsujimotter:20210501103139p:plain:w460

代数曲線としてのモジュラー曲線

これまでの話で、コンパクト化されたモジュラー曲線 $X_1(N) = \Gamma_1(N)\setminus H^*$ を考えたときに、そのカスプを除いた点全体は拡張された楕円曲線の同型類に対応することを示しました。すなわち、 $X_1(N) - \{\text{カスプ}\}$ は拡張された楕円曲線のモジュライ空間ということです。

一方で、代数曲線の一般論として、コンパクトリーマン面は代数曲線でもあるという事実があります。つまり、 $X_1(N)$ 自身も代数曲線でもあるというわけです。 $X_1(N)$ 自身が代数曲線でありながら、さらにその各点には楕円曲線の同型類が乗っているという「入れ子構造」を持っているわけです。これは大変面白い話ですね。

上記の一般論は、コンパクトリーマン面上の関数体を考えると理解できるかと思います。（この辺の理解は怪しいことを前置きしつつ） $X_1(N)$ の関数体を考えると、ある関数 $x, y$ を用いて $\mathbb{C}(x, y)$ とかけます。この関数体は超越次元が $1$ となっていて、つまり $\mathbb{C}(x)/\mathbb{C}$ は無限次元の拡大となっていて、 $\mathbb{C}(x, y)/\mathbb{C}(x)$ は有限次拡大になっているということです。したがって、 $f(x, y) = 0$ を満たす $f \in \mathbb{C}(x, y)$ が存在し、代数曲線が得られる（ということだと思います）。

たとえば、上の方で書いた楕円曲線の例を考えてみましょう。トーラス $\mathbb{C}/\Lambda$ 上の関数体を考えると、これが $\wp, \wp'$ を用いて $\mathbb{C}(\wp, \wp')$ と表せます。この関数体は超越次元が1であり、したがって代数的な方程式

$\wp'^2 = 4\wp^3 - g_2 \wp - g_3$

が存在して、これが楕円曲線の定義方程式となるわけです。

抽象的にはこのように理解できるわけですが、実は $X_1(11)$ が楕円曲線のモジュライであることを用いると、具体的な定義方程式を求めることができます。結果的には

$X_1(11)\colon y^2 + y = x^3 - x^2$

となります。

この方法は参考文献の三枝先生の記事に書かれている方法なので、詳しくはそちらを読んでいただきたいのですが、かいつまんで説明します。

楕円曲線 $E$ であって、位数 $11$ の点 $P$ を持つものを考えて、そのような $E$ の係数が従う条件を考えます。具体的に、点 $P$ を持つことを前提に、 $P = (0, 0)$ として座標を適当に取り直すことで

$y^2 + (1-b)xy - ay = x^3 - ax^2 \;\;\;\; (a, b\in \mathbb{C})$

という形に方程式の形を限定させることができます。ここで $11P = \mathcal{O}$ より $5P = -6P$ となるので、 $5P$ と $6P$ の $x$ 座標が等しいという条件によって、位数11の楕円曲線の係数 $a, b$ が満たすべき条件が表現されます。

あとは、得られた $a, b$ の関係式を適当に変数変換すると、 $y^2 + y = x^3 - x^2$ が得られるというわけです。

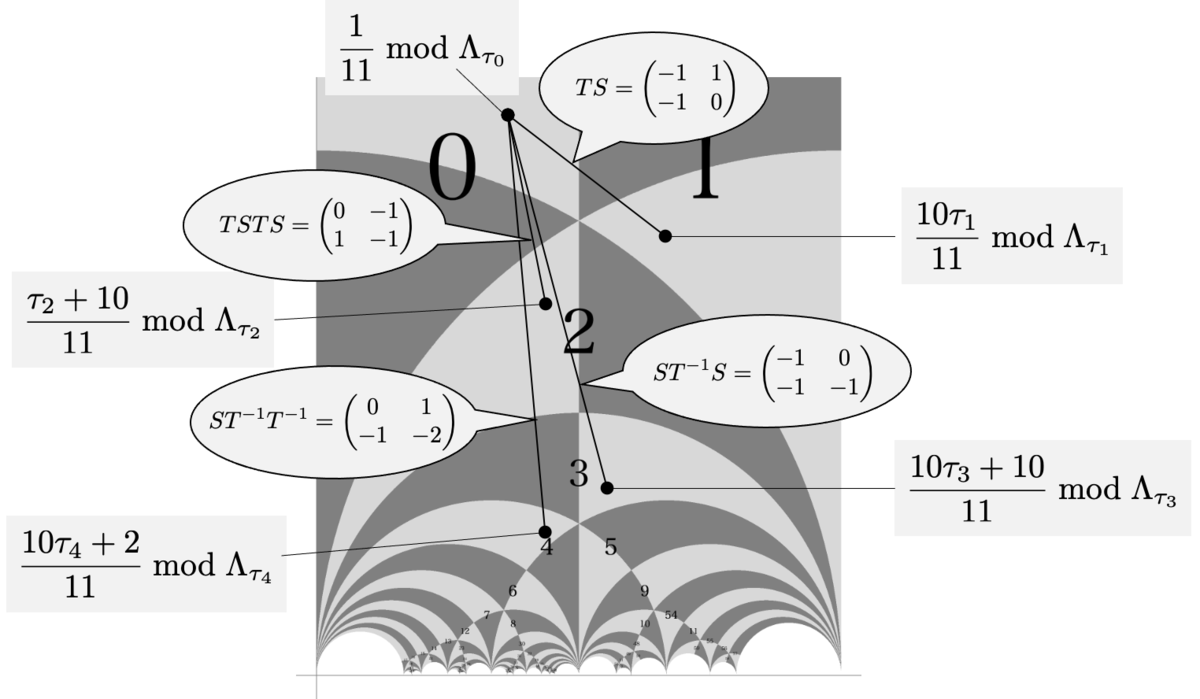
この変数変換の中で、すべての $y^2 + y = x^3 - x^2$ の点に対して、対応する $a, b$ があるわけはありません。具体的には5点

$\{\mathcal{O}, (0, 0), (1, 0), (0, -1), (1, -1)\}$

が対応する $a, b$ が存在しません。これらは $\Gamma_1(11) \setminus H^*$ のカスプに対応する点だと思うことができるようです。

したがって次のような対応関係が得られるというわけです：

$\begin{align} X_1(11) = \Gamma_1(11) \setminus H^* \;\; &\longrightarrow \;\; \{(x, y)\, \mid \, y^2 + y = x^3 - x^2 \} \cup \{O\} \\ \{ \text{カスプ} \}\;\;\;\; &\longrightarrow \;\; \{\mathcal{O}, (0, 0), (1, 0), (0, -1), (1, -1)\} \end{align}$

※ここがあまりよく理解できていないのですが、カスプが10点に対して、カスプに対応する楕円曲線 $y^2 + y = x^3 - x^2$ の点は5点になっているので、これはどういうことなんでしょうかね。

2:1で対応しているという話なのか、 $X_1(11)$ の中で $y^2 + y = x^3 - x^2$ に対応しない点があるということなのか。

この対応関係を通して $X_1(11)$ を代数曲線 $y^2 + y = x^3 - x^2$ だと思うことにしましょう。また、この場合の $y^2 + y = x^3 - x^2$ は $\mathbb{Q}$ 上の楕円曲線でもあります。

一般には $X_1(N)$ に対応する曲線は楕円曲線になるとは限りません。一方で $\mathbb{Q}$ 上の曲線になることは一般に言えるそうです。

ここで $y^2 + y = x^3 - x^2$ の有理点を考えてみましょう。

$(x, y) \in \mathbb{Q}^2$ なので、元々の楕円曲線の係数 $a, b$ も有理数に対応します。したがって、 $y^2 + y = x^3 - x^2$ の有理点であって、カスプに対応しないものは $\mathbb{Q}$ 上の楕円曲線と位数 $11$ の有理点 $P$ の組 $(E, P)$ の同型類に対応することになります。

具体的に $y^2 + y = x^3 - x^2$ の有理点を求めてみます。ランクは 0 であり、さらに位数有限の点は

$\{\mathcal{O}, (0, 0), (1, 0), (0, -1), (1, -1)\}$

の5点のみとなります。したがって、有理点全体は

$X_1(11)(\mathbb{Q}) = \{\mathcal{O}, (0, 0), (1, 0), (0, -1), (1, -1)\}$

となります。

なお、上記の点はすべて $X_1(11)$ のカスプに対応することになります。つまり、有理点に対応する $\mathbb{Q}$ 上の拡張された楕円曲線の同型類 $[E, P]$ は存在しません。

したがって、位数 $11$ の有理点を持つ楕円曲線は、存在しないことが証明できたというわけです！面白いでしょう！

ここまでの話を一旦まとめます。

位数 $11$ の有理点を持つ楕円曲線全体を考えるために、位数 $11$ の点を持つ楕円曲線のモジュライ空間 $X_1(11)$ を考えました。 $X_1(11)$ がこれまた楕円曲線になっていて、その有理点が $\mathbb{Q}$ 上の楕円曲線に対応します。さらに $X_1(11)$ に対応する楕円曲線にカスプ以外の有理点がないことがわかったので、位数 $11$ の有理点を持つ楕円曲線自体が一つも存在しないことが言えてしまったというわけです。

モジュラー曲線すごいですね！！

メイザーの定理

このように考えると、 $N \neq 11$ のときも同じように考えられそうですね。つまり、モジュラー曲線 $X_1(N)$ の定義方程式を求めて、その有理点が存在するかどうか調べれば良いという方針です。

一方で、モジュラー曲線の種数の情報を調べることで、具体的な方程式を求めずとも、ある程度は有理点に関する情報もわかってしまいます。

$\Gamma_1(N) \subset \Gamma$ なので、 $X_1(N)$ から $X(1)$ へは標準的な全射が存在します。この全射がコンパクトリーマン面の間の被覆写像となっていて、リーマンフルヴィッツの定理によって $X_1(N)$ の種数が得られます。

実際、（私は具体的に計算していないのですが）

$N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12$

においては種数が $0$ となるそうです。

たとえば $x^2 + y^2 = 1$ は種数 $0$ ですが、有理点 $P_0 = (-1,0)$ を1点持ちます。点 $P_0$ を通る直線を考えると、直線の傾きが有理数 $t$ であれば、直線と円のもう一点の交点 $P_t$ も有理点となります。

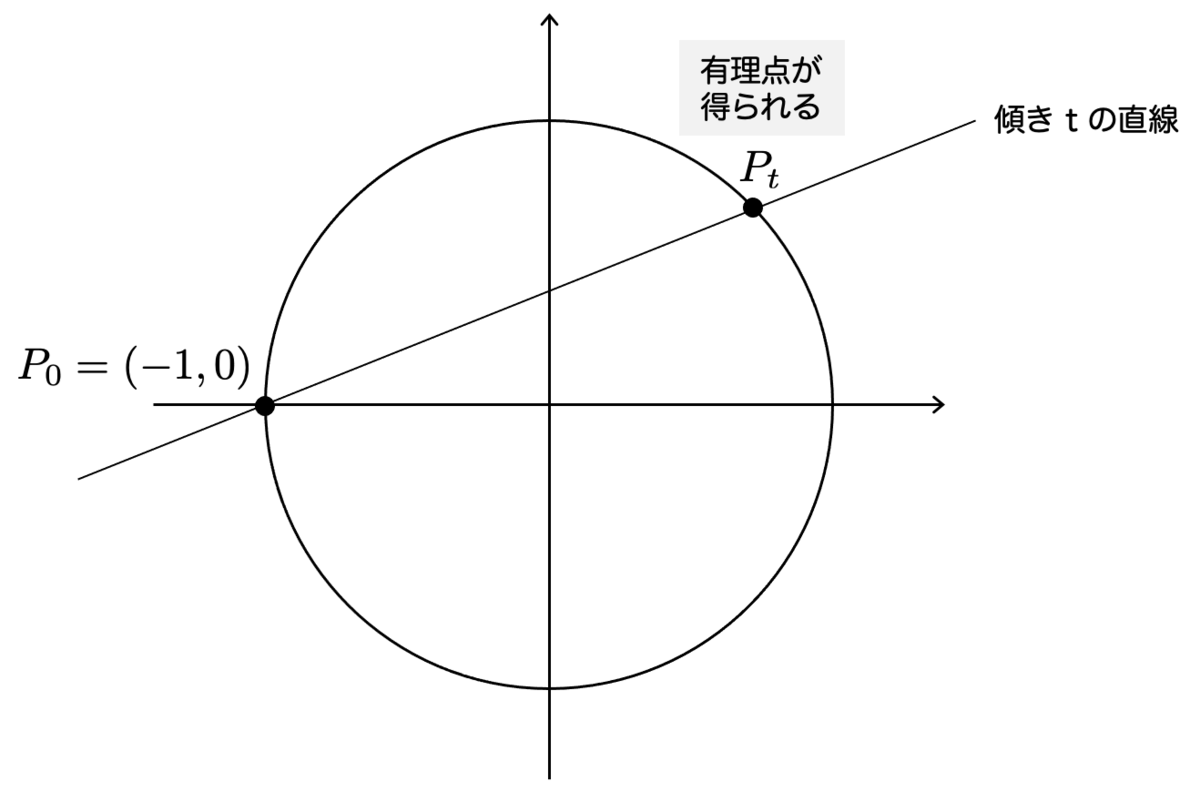
f:id:tsujimotter:20210501105200p:plain:w360

直線の傾き $t\in \mathbb{Q}$ に対し、直線のもう一方の交点 $P$ を対応させることで、 $x^2 + y^2 = 1$ の有理点と $\mathbb{P}^1(\mathbb{Q})$ を一対一対応させることができます。よって、無数に有理点が存在することが示せるわけですね。

有理点が１つも存在しない場合は（たとえば、 $x^2 + y^2 = 3$ ）、この方法は使えず、有理点は１個も存在しないということになります。

一般に種数 $0$ の代数曲線については、1つも有理点が存在しないか、あるいは、無数に有理点が存在するかのいずれかになります。

$N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12$ に対して、それぞれ位数 $N$ の有理点を持つ楕円曲線を具体的に挙げることができるので、この場合の $X_1(N)$ には少なくとも有理点が1個以上存在することがわかります。したがって、上記の方法により、無数に有理点があることがいえます。 $X_1(N)$ のカスプは有限個しかありませんので、位数 $N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12$ の有理点を持つ楕円曲線の同型類は、無数に存在することが言えます。

これ以外の $N$ についてはどうでしょうか。実は、カスプに対応しない有理点は存在しないことが示されています。これが冒頭に紹介したメイザー定理です。 $N = 13, 14, 15, \ldots$ と無限に調べていっても、どこにもカスプ以外の有理点が存在しないことが言えるわけですね。よって、対応する $\mathbb{Q}$ 上の楕円曲線も存在しないと言えるわけです。凄すぎますね！