この記事は iBeacon Advent Calendar 2013 の 22日目の記事です。
本当はestimoteを使って遊んでみた系の記事を書こうと思っていたのですが、とある事情で日本では使えないとのことで、仕方なく方針を変えて私の知っている知識を紹介したいと思います。(あまりiBeaconっぽい話じゃなくてすみません)
背景
タイトルの通り「iBeaconの電波強度 (RSSI) の測定値を使って正確な二次元座標を取ろう」という目論見です。
iBeaconではRSSIの値を使ってビーコンまでの距離が計算できますが、ざっくりとした近い・遠いの情報しかわかりません。
これをもっと精度よく、二次元座標がとれたらいいなと思った訳です*1。
RSSIを使った測位手法の中で、比較的精度の高い位置が得られる方法として、フィンガープリンティングという手法があります。iBeacon で実例がありませんので*2、iBeacon Calendar的に参考になるかわかりませんが、方法の一つとしてこんなものがあるよ、ということで紹介したいと思います。
今回は、iBeaconを使っての実験・実装をまったくしていません。
参考になさってかまいませんが、iBeaconで動作することを保証するものではありません。
近いうちにこの方針でうまくいくかどうか実験してみたいと思っています。
そもそもRSSIから位置を計算するということ
RSSIは、Beacon端末から距離が遠くなればなるほど、小さい値を取ります。
電波の遮蔽がなく理想的な環境で、RSSIは次のような距離 r との関係式に従うといわれています。
ここで A は 1m 付近で計測される RSSI で、B は電波の減衰の度合いを表す定数です。
B は理論的には 2 となることが知られています。
RSSIが分かれば、この式から逆に端末までの距離が計算できます。
3点の端末からの距離が分かると、2次元平面上の位置が計算できます。これが三点測量です。
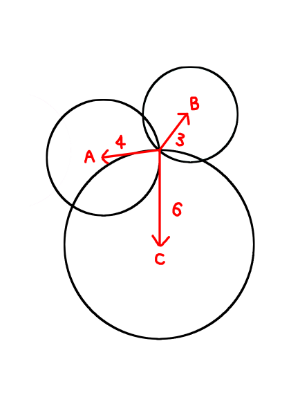
図のように、コンパスを使って、三点からのそれぞれの距離の円を書いてあげれば、交点となった部分が正解の位置となります。
昔算数で習った方法と同じです。
なぜ三点測量ではダメなのか?
Appleのドキュメントにも「RSSIを使って正確な位置は出せない」というような内容が書かれているそうですが、これはどういう意味なんでしょう。
電波は部屋の中で反射します。反射した電波が互いに重なって干渉します。これをマルチパスといいます。干渉した電波は、位相差に応じて強め合ったり弱め合ったりします。これがノイズとなるわけです。
このノイズの影響は非常に大きくて、たとえばWi-Fiで計測した結果では、大きいところでは 20 dBm 程度もかわってしまうこともあります。この影響によって距離の誤差は10m以上になることもあります。
また、マルチパスのほかにも部屋の壁で遮蔽されたり、RSSIを前述の式から外してしまう環境の要因はたくさんあります。
距離に大きな誤差が乗っていれば、当然三点測量の結果も悪くなってしまいますね。
フィンガープリンティング
RSSIの値は、計算では簡単には出せません。環境によってマルチパスの影響が異なるからです。
「計算によって予想できないのであれば、実際に測ってしまえばいい」というシンプルな考え方に基づく測位手法がフィンガープリンティングです。
部屋の中をグリッドに区切って、各点上でRSSIを事前に計測します。
それぞれの点の位置と対応するRSSIの組み合わせをフィンガープリントといいます。
各点のフィンガープリントを保存しておき、それを測位に用いるのです。
測位時には、観測されたRSSIと事前計測したフィンガープリントを比較して、RSSIがもっとも近いフィンガープリントの位置を出力します。
この方式をNearest Neighbors法と呼びます。最も近いご近所さんということです。
Nearest Neighbors法のほかに、k-Nearest Neighbors法というものもあります。
まず、RSSIが近い順にフィンガープリントをソートします。このとき、前から i 番目のフィンガープリントまでのRSSI上の距離を 、そのフィンガープリントの座標ベクトルを
とします。
次に、前から k 個のフィンガープリントを使って次のような和を考えます。
これがフィンガープリンティングの出力する位置となります。kはフィンガープリントの全体の数に応じて実験的に決めます。
フィンガープリンティングは実際のデータを計測しているので、計測点の数を十分に取れば前述した三点測量より精度の高い位置が計算できます。ただし、事前の計測が必要になり、計測点の数が大きければ準備に時間的なコストがかかります。先行研究をみる限りでは、だいたい1mから3m程度のグリッドに区切って計測しているようです。
まとめとちょっと言い訳
三点測量では、RSSIと距離の関係を式で近似してそれをもとに位置を計算します。しかし実際は、RSSIの値は単純には決まりません。
そこで実際に計測してそのデータ(フィンガープリント)を使って位置を計算しようというのがフィンガープリンティングという手法です。フィンガープリンティングは三点測量と比べて精度の高い手法ですが、その分事前の計測も面倒な方法です。ここら辺は、一長一短ですね*3。
フィンガープリンティングを実装した iBeacon アプリを作りたかったのですが、ビーコンの技適的な意味で断念してしまいました。今回の記事では「妄想編」ということでご容赦ください。
そのうち問題が片付いたらちゃんと実装してみたいと思います。
早いとこ iPhone アプリの開発の方法を勉強します。
(技適の話はどうしよう。。。)
参考文献
英語の論文ですが、k-Nearest Neighborsを使った測位手法の論文です。
[1] Evennou, F. and Marx, E, Advanced integration of WIFI and inertial navigation systems for indoor mobile positioning, EURASIP Journal on Applied Signal Processing, Vol. 2006, pp. 164-174 (2006).
フィンガープリンティングと三点測量を混ぜた手法の論文です。
[2] J. Lloret, J. Tomas, M. Garcia and A. Canovas: A hybrid stochasticapproach for self-location of wireless sensors in indoor environments,Sensors(Basel, Switzerland), Vol. 9, No. 5, pp.3695-3712 (2009).
*1:サービスレベルでは近い・遠いで十分かもしれませんが、正確なナビゲーションや行動心理学での人の移動軌跡の分析とか実験的にはいろんな応用があるんじゃないかなと思っています。
*2:iBeacon では Bluetooth を使って通信していますが、私が知っている限りでは、Wi-Fi, ZigBee などの無線通信においてフィンガープリンティングで測位できることが示されています。たぶん BlueTooth でも同様に測位できるのではないかと思います。(ここでいう「測位できる」とは1m-3m 程度の誤差で位置が推定できるということです。)というのも、Wi-FiにしてもZigBeeにしてもBlueToothにしても使っている電波は同じ2.4GHz帯のものであり、電波の性質の多くはその周波数によって決まるからです。
*3:ハイブリッドにしようという手法もあります