今日考えたいのは 銅錯体 についてです。
硫酸銅は2価の銅イオン と硫酸イオン
のイオン結晶
です。これ自体は白い粉なのですが、水に溶けると 青色 に呈色します。
飽和量以上の硫酸銅を加えると結晶が析出しますが、その結晶の色も綺麗な 青色 となります。硫酸銅(Ⅱ)五水和物と呼ばれるもので、化学式で書くと
となります。これは、2価の硫酸銅に5つの水分子 が配位結合していることを表します。(あとで配位結合とは何かについては説明します。)
実際を見てみると、とても綺麗な色をしていますね。

(ちなみに、こちらは自分で買った私物です。笑)
硫酸銅の水和物は高校化学でも扱うので、化学好きの人にはおなじみかもしれませんね。
※なお、硫酸銅の結晶は毒性がありますので、購入を希望される方はよくよく調べた上で、取り扱いには十分ご注意ください。
水溶液の中の銅も、結晶の方の銅も、どちらも 錯体 と呼ばれる種類のものになっています。今日考えたいテーマは
です。
今日も色について深く掘り下げていきたいと思います!
YouTubeで「硫酸銅五水和物」等で検索してみると、硫酸銅(Ⅱ)五水和物を加熱することで、無水結晶が得られることを示す実験動画が紹介されています。
水が加わることで結晶が青色に変化することが見て取れますね。いったいどうして、水が加わると青色にかわるのでしょうか?
色の仕組みを紐解く上で、重要なキーワードは 2つ です。
一つは d軌道 です。前回までは、ほとんど炭素しか扱わなかったので、d軌道は登場しませんでした。遷移元素と呼ばれる元素の性質は、このd軌道がとても重要です。
また、もう一つのキーワードは 群論 です。色の仕組みを説明するのに群論が使えるというのは、私にとって大変驚きの事実でした。群論は「対称性」についての学問だといってよいと思いますが、今回は 分子と軌道の対称性 を追求します。
大変面白い話だと思いますので、よろしければ最後までお付き合いください。
前編の目次:
だいぶ長い記事になってしまいますので、前後編 に分けたいと思います。前半ではd軌道によって色が現れる仕組みについて説明します。後半では群論との関係についてまとめたいと思います。
(明日公開予定です。→既に公開されています!)
前回「植物の葉の色はなぜ緑色か?」という記事を書きました。
tsujimotter.hatenablog.com
調べ物をするにあたって、キリヤ化学さんのウェブサイトにある「色と化学についてのQ&A」に大変お世話になりました。
www.kiriya-chem.co.jp
このサイトは本当に素晴らしいサイトで、色についての本当にさまざまなトピックが質問に対する解説という形でまとまっています。植物の話とは関係なく、いろいろな記事を読み漁ってしまいました。
その中で心を惹かれたのが、硫酸銅の青色についての話です。
www.kiriya-chem.co.jp
この内容があまりに面白かったので、本物の結晶が欲しくなり、即座に購入を決めました。届いたのが冒頭で紹介した結晶です。
なんて綺麗なんだろう。そもそも自然界に、ここまで綺麗なブルーをしているものはあまり多くないので、その意味でも新鮮ですね。
そんな経緯で青色になる仕組みに関心を持ったtsujimotterですが、やはりきちんと原理を勉強してみたくなりました。
化学系の入門書(特に錯体化学系のもの)を調べて、ある程度自分でも説明できそうなところまできたので、まとめてみたというのがこちらの記事になります。
1. 錯体と配位結合
まず、基本的な事項をおさえるために、高校化学レベルの「錯体とは何か」という話から始めたいと思います。
錯体の「錯」という漢字は「まじる」の意味があります。錯体とは「金属と非金属がまじりあって結合された化合物」のことを指します。
高校化学では、無機化学(金属)や有機化学(非金属)に分けて考えることが多かったと思いますが、これは両者の分野の性格の違いによるところでしょう。異なる分野を結びつけるのが錯体化学ですから、難しくなりますし、それゆえに興味深い対象になります。
参考文献の山口先生の記事に、錯体化学を表現する素晴らしい一文が書かれていたので紹介したいと思います:
錯体化学は『金属元素(無機化学)と有機物からなる配位子(有機化学)を組み合わせることで,新しい美しさや優れた機能を発現する』学問であるといえる。
山口佳隆「金属錯体の形と色」より
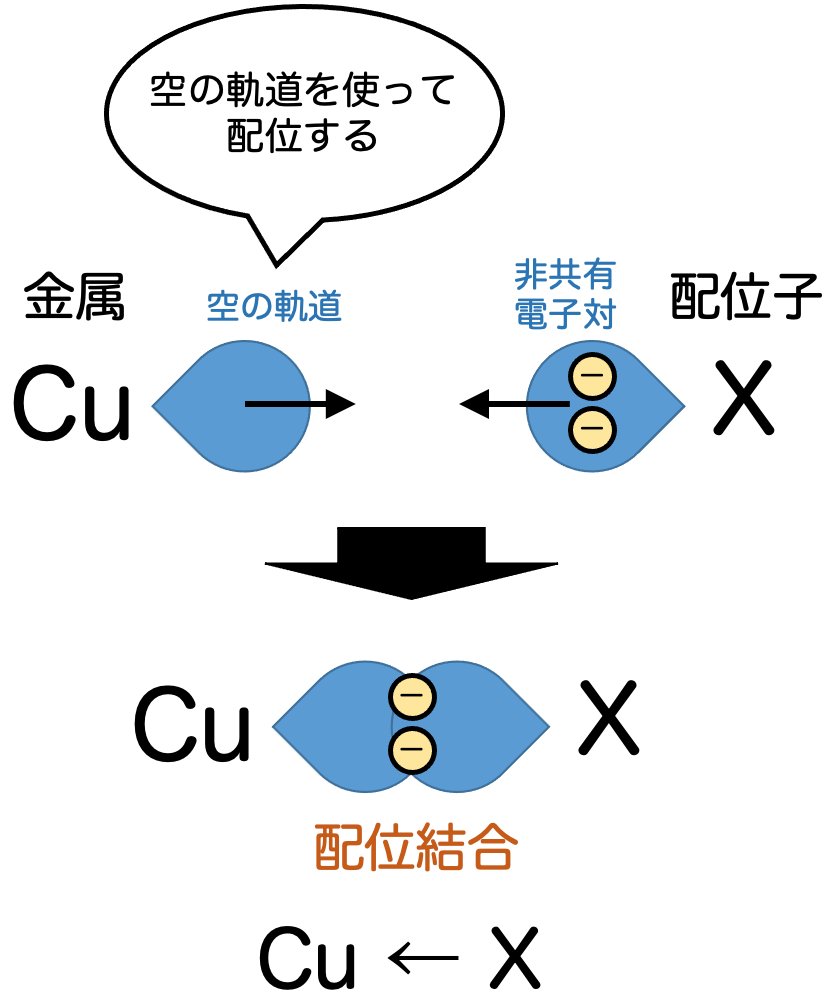
さて、金属と非金属の間の結合には、配位結合 が用いられることが多いので、それについて説明しましょう。配位結合は共有結合と対になる概念なので、両者を比較して説明します。
共有結合とは、2つの原子核のそれぞれの軌道に1個ずつある電子を共有されることで生じる結合のことでした。
一方の配位結合は、結合は非対称的です。片側の軌道は電子がない空の状態です。もう一方は、軌道に電子が2つ入っている状態とします。これを孤立電子対といいます。この孤立電子対を、他方の空の軌道に差し出すような形で結合が形成され、これを配位結合といいます。

この結合は上に書いたように非対称的であり、電子を差し出す側から、差し出される側に向かって矢印を引いて表すことが多いです。
配位結合において、電子を差し出す側を配位子といいます。電子を差し出される側が金属であるときに、金属錯体になるというわけです。
2. 銅(Ⅱ)錯体の構造
さて、硫酸銅を水に溶かして得られる銅(Ⅱ)イオンや、硫酸銅(II)五水和物の結晶は、いったいどのような構造をもった錯体なのでしょうか。両者で錯体としての構造は異なるので、順に説明します。
まず、水に溶かした場合から。
硫酸銅 を水に溶かすと、2価の銅イオン
と硫酸イオン
に分かれます。銅イオンはこのまま水の中を漂っているわけではなく、実際は水分子
が、銅イオンのまわりに配位した水和物として存在しています。つまり、水分子が配位子として、銅イオンに配位結合しているというわけですね。
高校化学では、銅イオンは4つの水分子と水和して錯イオン を形成していると習います。4つの水分子の位置関係を調べてみると、図のように「正方形」の形に配位しているようです:
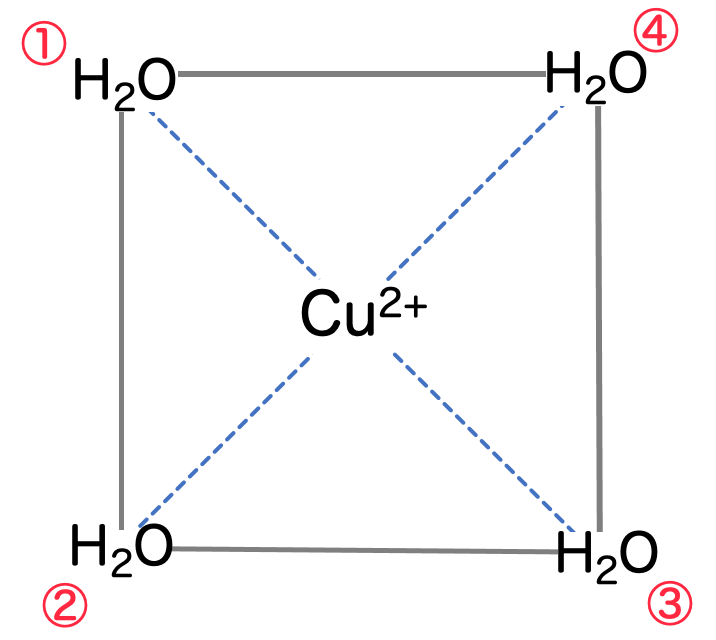
これは少し意外に思うと思います。というのも、4つの分子が配位しているのであれば、もっとも対称的なのは「正四面体(テトラポットのような形状)」のように思えるからです。
これには理由があって、実際は水分子はもう2つ配位していて、それぞれ正方形の上下に立体的に配位しているからです。
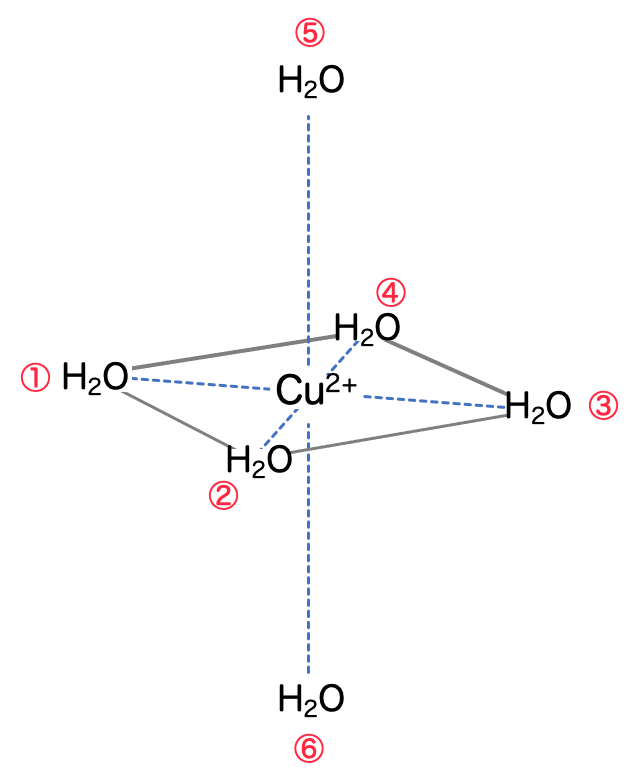
つまり、6配位しているわけですね。立体的な形状は 八面体 です。
正八面体ではなく、正八面体をz軸方向に引き伸ばしたような形 をしているのがポイントです。
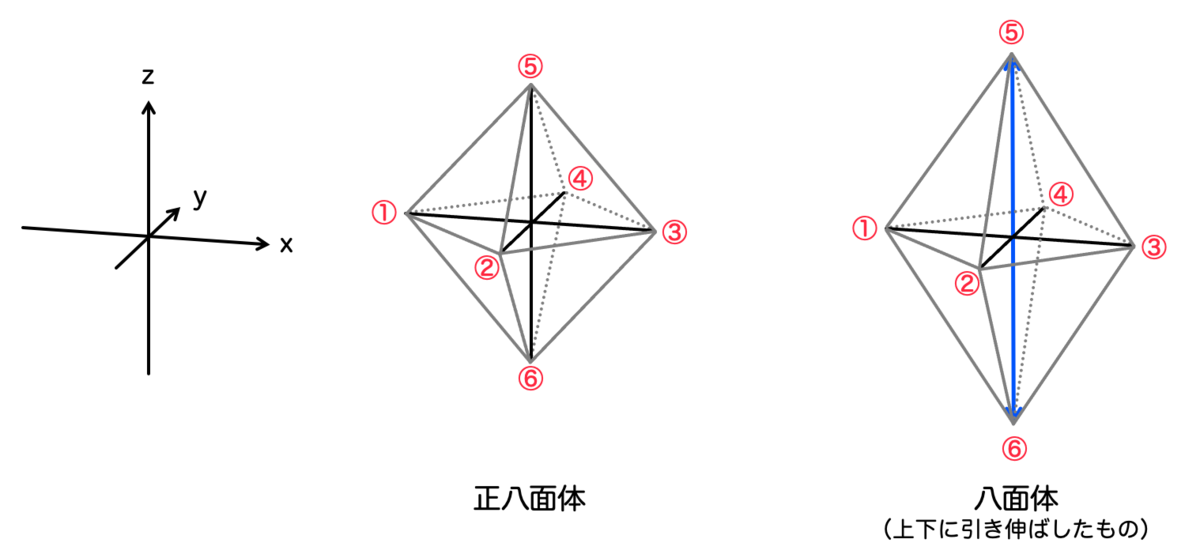
不思議なことに、この形状がどうやら安定なようなのです。(あとで理由を説明します。)
z軸方向の水分子は、xy平面のものと比べて銅原子からの距離が遠くなっているため、これにより影響が相対的に小さくなります。そこで、上下の2つは忘れて「正方形の形に配位している」と言うこともあるわけですね。
そんなわけで、基本的には八面体の頂点に配位していると考えることにします。
一方、硫酸銅(Ⅱ)五水和物の結晶の方はどうでしょうか。
調べてみると、銅(Ⅱ)イオンのまわりに平面正方形の形で水分子が配置されるようです。そして、z軸の上下のやや離れたところに が配位されます。
基本的な構造としては、銅(Ⅱ)イオンのまわりにやはり 八面体 に配位されるということですね。
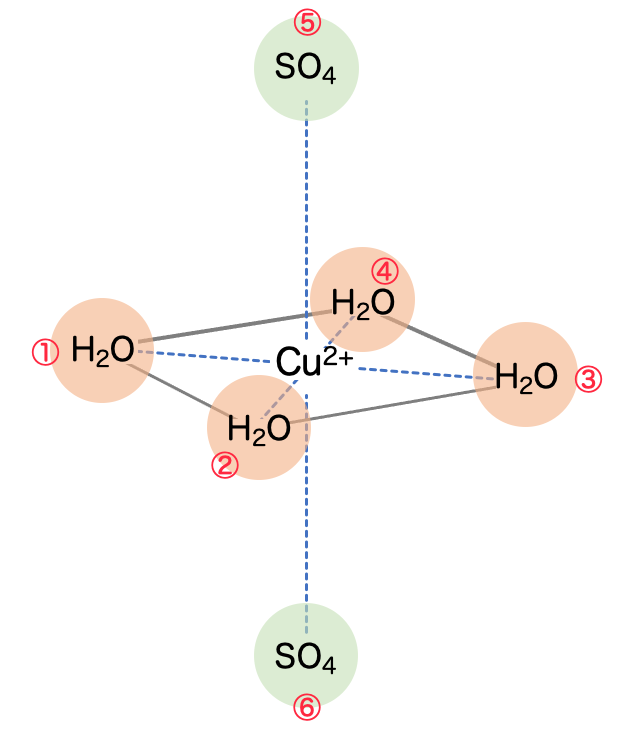
と
が交互に並ぶ形で結晶が構成されます。
ところで、銅イオンに4つの水分子が配位しているわけですが、これだと1つ足りない気がしますね。残り1個の水分子がどこにいったかというと、これは結晶の隙間に入り込む形で入っているそうです。
いずれにしても、水に溶かした場合も水和物の結晶に関しても、どちらも銅(Ⅱ)イオン を中心とする金属錯体であり、6つの配位子が立体的に八面体配位されている点が共通しています。
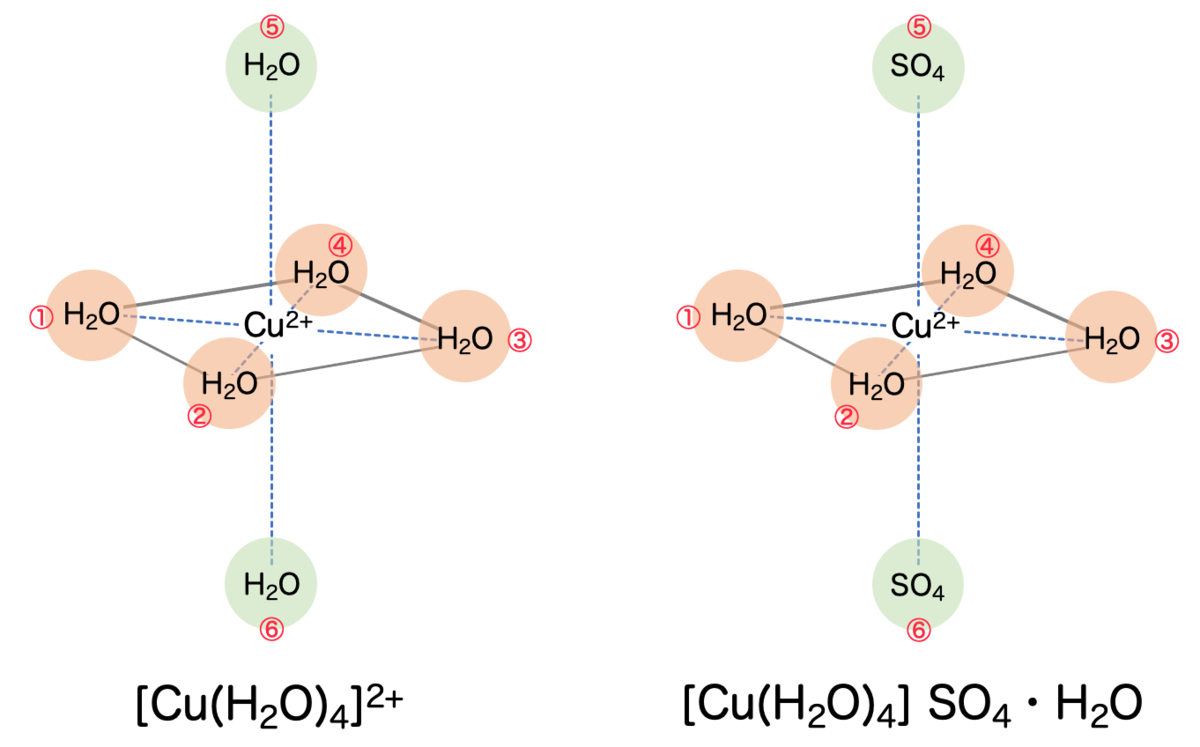
また、単純な正八面体ではなく「正八面体を上下に引き伸ばした図形」になっている点も特筆すべき点です。
正八面体配位する金属が多い中で、そうならないのは銅元素の特徴でもあります。この性質は銅の持つ電子の個数によるところがあります。
このあたりの話は本当に複雑で、調べていくうちに次々認識がアップデートされていきました。結果として、このブログ記事も公開前に一度大幅に書き換えています。「銅」という元素を選んだしまったことを少し後悔しました。なんで、もっと簡単なものを選ばなかったのだろう。笑
今日扱いたいのは、この金属錯体がなぜ青色をしているかということですね。
単純に真空中に置かれた銅イオンを考えると、これは青色をしているわけではないのは硫酸銅の無水物の観察からもわかります。したがって、周りにいる6つの配位子の影響を受けて青色になっているのではないかと予想されます。
いったいどのようにして、配位子が色を生み出しているのでしょうか。以下では、その仕組みを解き明かしていきましょう。
3. 色と電子
物質に色がつくメカニズムはさまざまなものが考えられます。要因を調べていくと本当に多様でキリがないなと感じますが、これが色という概念の奥深さかと思います。
今回、特に考えたい色のメカニズムは 光の吸収 です。
前回の記事「植物の葉はなぜ緑色か?」で解説したように、光は電磁波の一種であり、その波長に応じて人間が感じる色が変わるのでした。
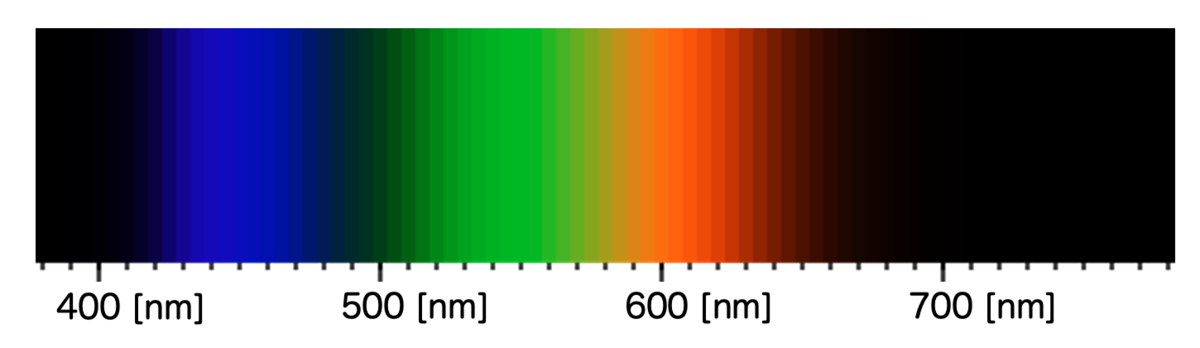
物体に可視光が当たったときに、特定の色の光を吸収するのであれば、その補色となる色が見えます。今回のケースであれば、硫酸銅(Ⅱ)五水和物の結晶が赤〜緑にかけてのいずれかの色の波長を選択的に吸収します。結果として、補色である青色が見えるわけです。
では、硫酸銅(Ⅱ)五水和物の結晶は、なぜ赤〜緑にかけての波長の光を吸収するのでしょうか。その謎を解く鍵は、電子 にあります。
電子が原子核のまわりにいるとき、電子の取りうるエネルギーが飛び飛びの値になることは「植物の葉はなぜ緑色か?」の記事で説明しました。
一方、光は波であると同時に、エネルギーの塊でもあります。電子に光が入射されると、光からエネルギーを受け取ることがあります。このとき、現在いるエネルギーの状態(基底状態)から、受け取ったエネルギーの分だけ高いエネルギーの状態(励起状態)に遷移します。これが光の吸収です。
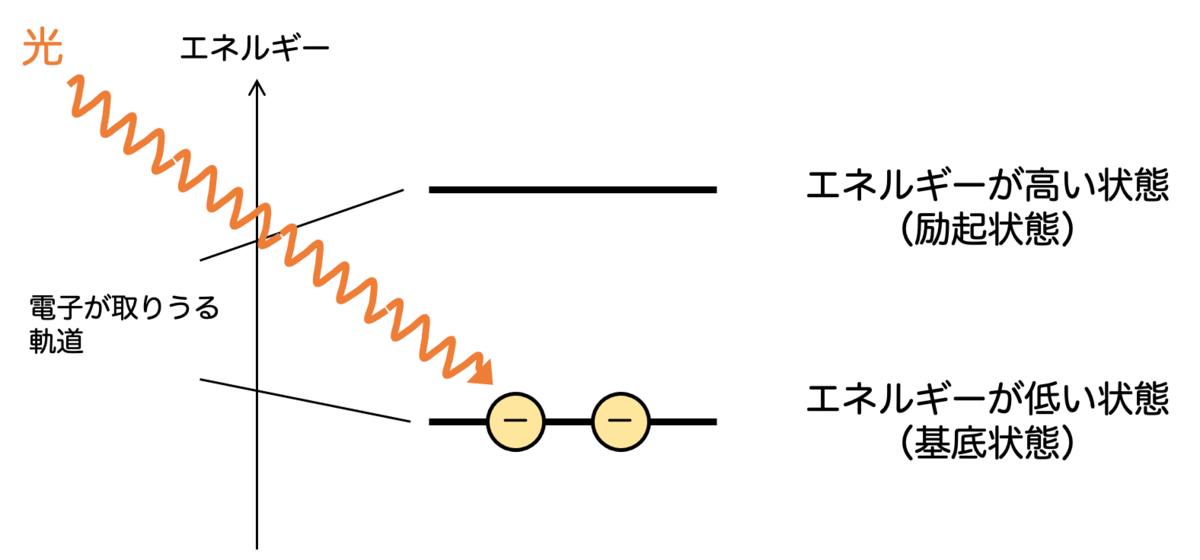

しかしながら、電子のエネルギーは決まった値しかとることができないのでした。つまり、基底状態と励起状態のエネルギーの差と、ちょうどぴったり一致するエネルギーの光しか吸収することができないのです。
光のエネルギー は、波長
によってのみ決まります。プランク定数
と光速
を用いて
と表されます。つまり、波長がちょうどよい光しか吸収できないというわけですね。
これが特定の波長の光を選択的に吸収する仕組みというわけです。
4. 銅の電子配置
光の吸収を調べるには、電子の取りうるエネルギーを知る必要がありました。
そこで、まずは銅原子単体の原子軌道について考えましょう。
上記の2つの記事で議論したように、水素様原子(電荷 を持つ原子核1つと、電子1つ)におけるシュレーディンガー方程式
を解きます。シュレーディンガー方程式の解を波動関数と言います。
これが解を持つようなエネルギー は飛び飛びの値となり、量子数
と呼ばれる3つの非負の整数の組に対応する解
が得られるのでした。
下から順に量子数
に対応する軌道を
4s軌道、4p軌道(×3)、4d軌道(×5)、・・・
のように名前をつけます。
(今回扱うのは銅なので、登場するのはここまでです。)
また、 を特に主量子数というのですが、主量子数
を「K殻」、
を「L殻」、
を「M殻」、
を「N殻」と呼びます。
(高校でおなじみの呼び方ですね。)
各軌道ごとに電子の分布が異なりますが、それを図示したのが次の図です:
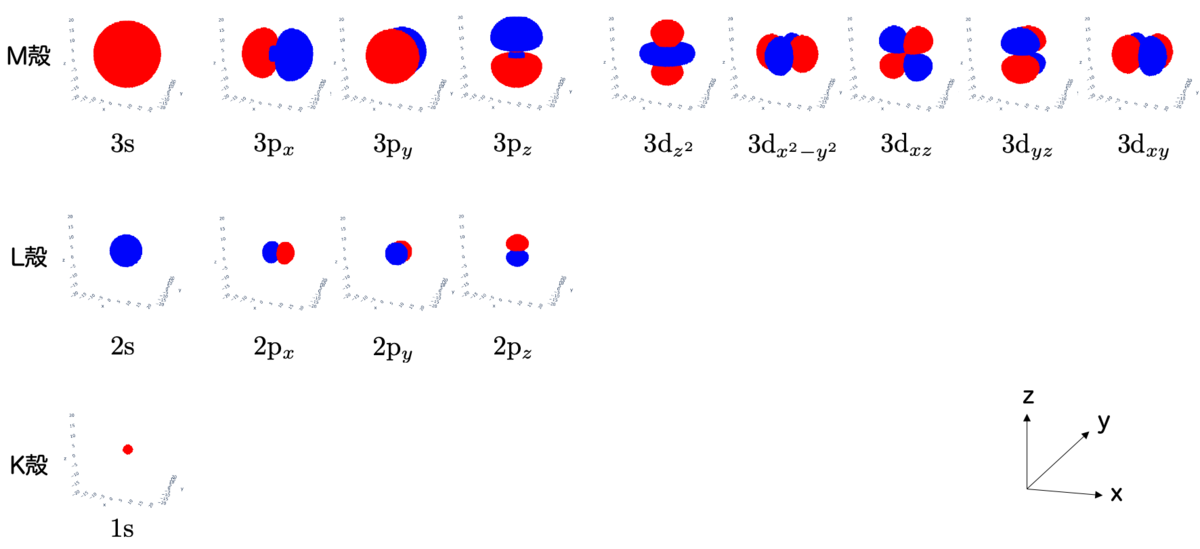
また、各軌道のエネルギーをグラフに載せると、こうなります:
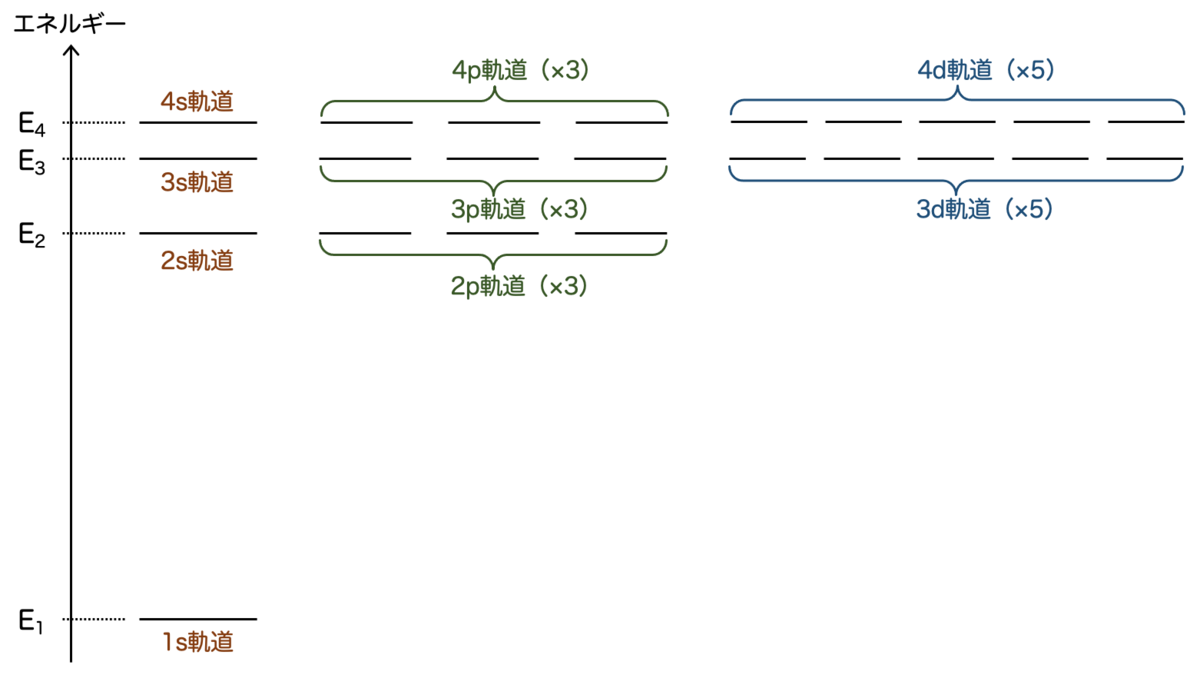
グラフを観察すると、たとえば2s軌道と2p軌道 (×3) は同じエネルギーになっています。
水素様原子の場合は、一般にエネルギーは主量子数 によってのみ決まり、
が同じ軌道は同じエネルギー
をとります。
は
に比例することが計算できます。
このように、別々の軌道が同じエネルギーを持つことを 縮退している と表現します。つまり、2s軌道と2p軌道は縮退しているというわけですね。
一方で、実際の原子を考えると電子が1個という状況ではないわけですね。銅は原子番号が29となりますので、29個の電子 を有することになります。
この電子が各軌道に入るわけですが、先に入った電子は原子核からのクーロン力を弱める形で、他の原子に影響します。
このことを考慮して再計算すると、たとえば銅の場合の実際のエネルギーは次のようになるそうです:

(なお、この図は各軌道のエネルギーの上下関係を表した図であり、エネルギーの値は正確ではありません。)
つまり、水素様原子においては同じエネルギーだった2s軌道と2p軌道は、もはや別のエネルギーになってしまうということですね。縮退が解ける というわけです。同様に、3s軌道、3p軌道、3d軌道の縮退も解けます。
面白いことに、主量子数の順にエネルギーが並ぶわけではなく、たとえば
のように、3d軌道と4s軌道が入れ替わります。
さて、銅の電子29個は、基底状態ではエネルギーの低い軌道から順に入っていきます。
各軌道には2つずつの電子が入り、既に2つの電子が入っている軌道には他の電子は入れません。電子は次に高いエネルギーの軌道に入ることになります。
この要領で29個の電子を入れていくと、次のような図が得られます:
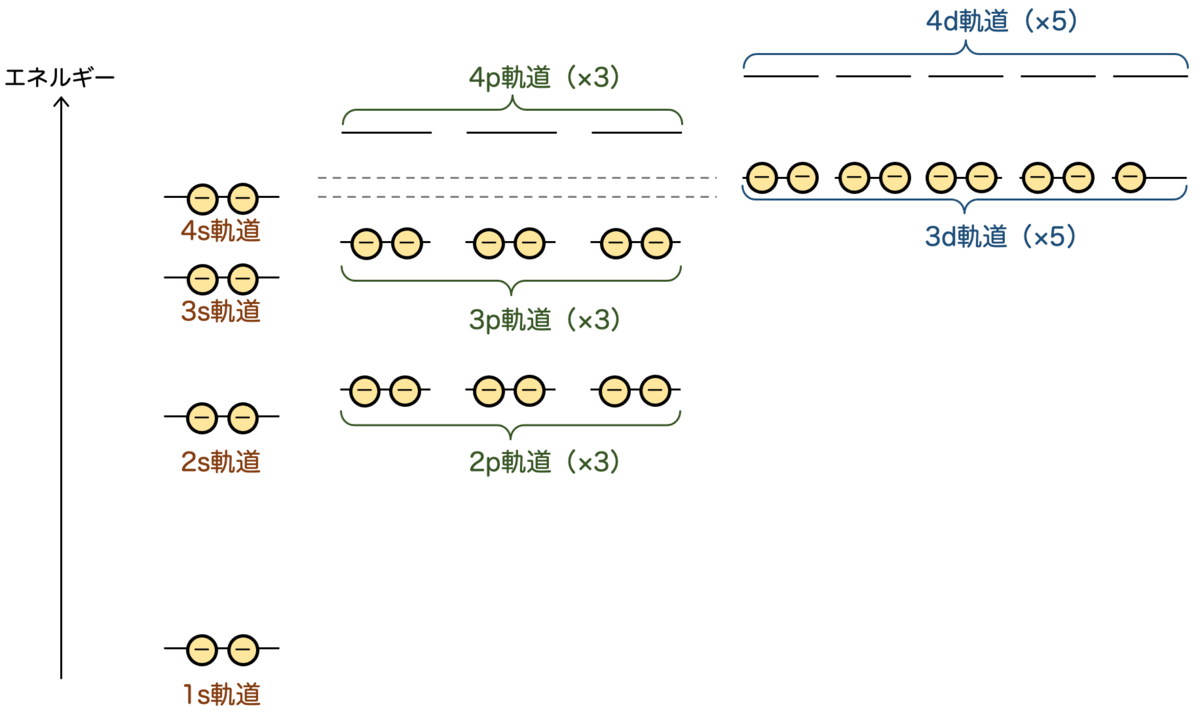
先ほど説明したように、エネルギーの逆転現象により4s軌道 < 3d軌道となりますので、4sが2個埋まってから、残り9個の電子が3d軌道に入ることになります。
一方で、最外殻は のN核になりますので、最外殻電子は4s軌道の2個 となります。価電子は2個 ということになり、この2個がしばしば反応に使われることになります。
銅がイオン化するときは、2個の最外殻電子が外れて2価の正イオン になるというわけです。内側の軌道(この場合は3d軌道)が埋まっていないのに、その外側の電子が最外殻となり、これが反応に使われるというのが面白いですね。
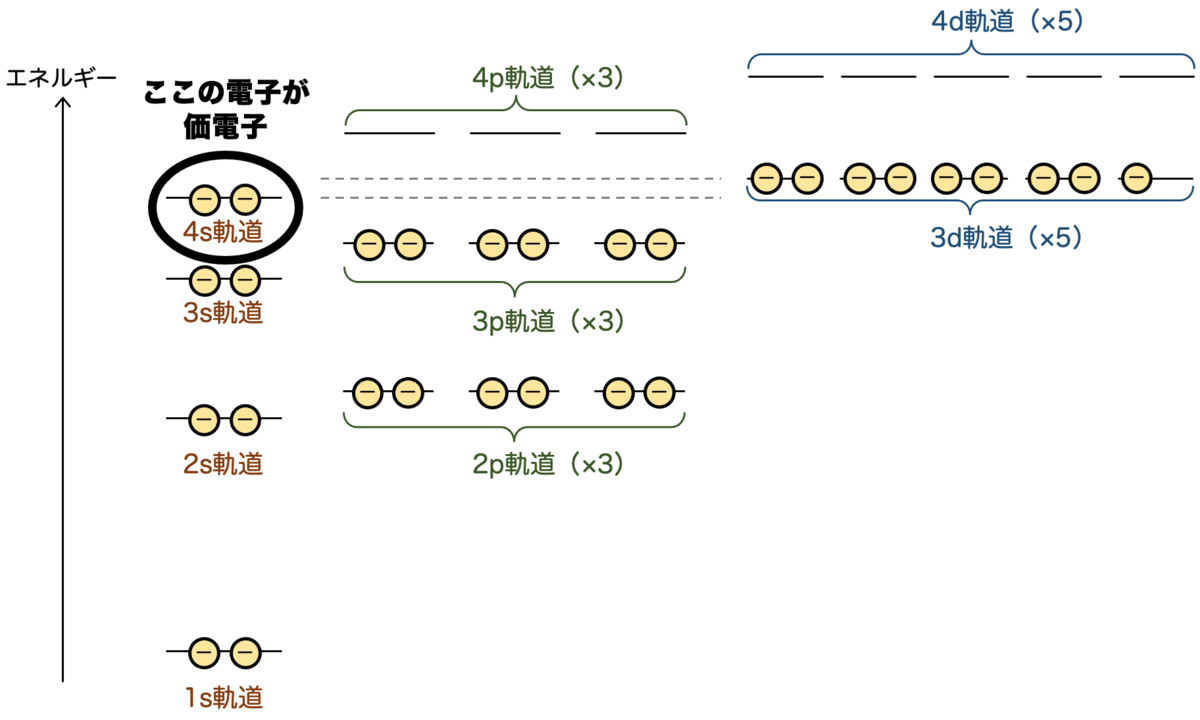
とはいえ、4s軌道と3d軌道のエネルギー差はかなり小さいので、4s軌道の電子はしばしば3d軌道に入ります。すると、価電子は1個ということになり、銅は1価の正イオン にもなり得ます。面白いですね。
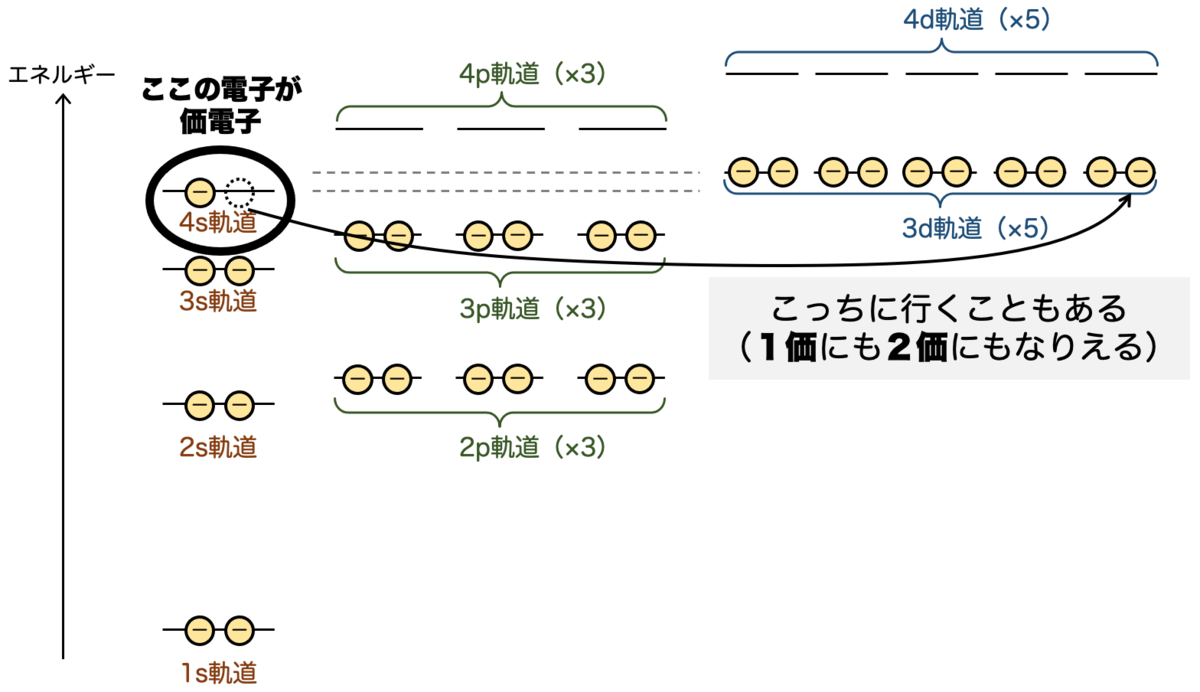
ところで、銅のケースと同じ様に考えると、原子番号20〜30においては、4s軌道に常に2個の電子が入った状態で、d軌道に1個ずつ電子が入っていくことになります。つまり、この間は 価電子がずっと2のまま となります。
これはかなり面白い状況で、原子番号20までは原子番号が1増えるごとに価電子の数が変化していました。一方で、20〜30まではずっと価電子が一緒であるというのです。
周期表は通常、縦の列の価電子が一致して、同じ列の元素は似たような性質を有するわけです(周期性)。しかし、原子番号20〜30においては、横方向に同じ価電子を持つ元素が続き、したがって横方向に似たような性質を有することになります。このような元素のことを 遷移元素 といいます。
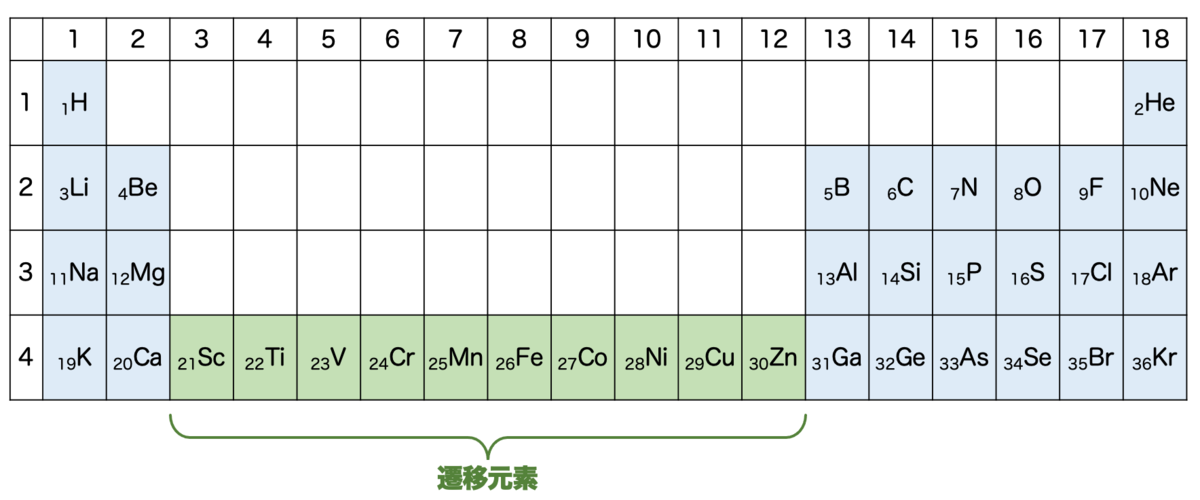
遷移元素はまさに d軌道の特殊性の現れ です。3d軌道と4s軌道の逆転があったからこそ起きた面白い現象というわけですね。
ちなみに、4d軌道のときも同じ様に遷移元素が発生します。遷移元素はすべて金属元素であり、金属の持つ独特な性質はd軌道によるところが大きいです。
銅イオンの電子の取りうる軌道がわかったわけですが、これによって青色になる仕組みは理解できるでしょうか。
実は、ここまでの議論ではまだ不十分です。銅イオンの取りうる原子軌道を考慮しても、青色になる仕組みが説明できないのです。つまり、ちょうどよいエネルギー差の軌道がないというわけです。
青色になる仕組みを説明するためには、配位子による影響を考える必要が出てきます。
5. 八面体配位と混成軌道
ここからは2価の銅イオン のまわりに、配位子を配置していきましょう。
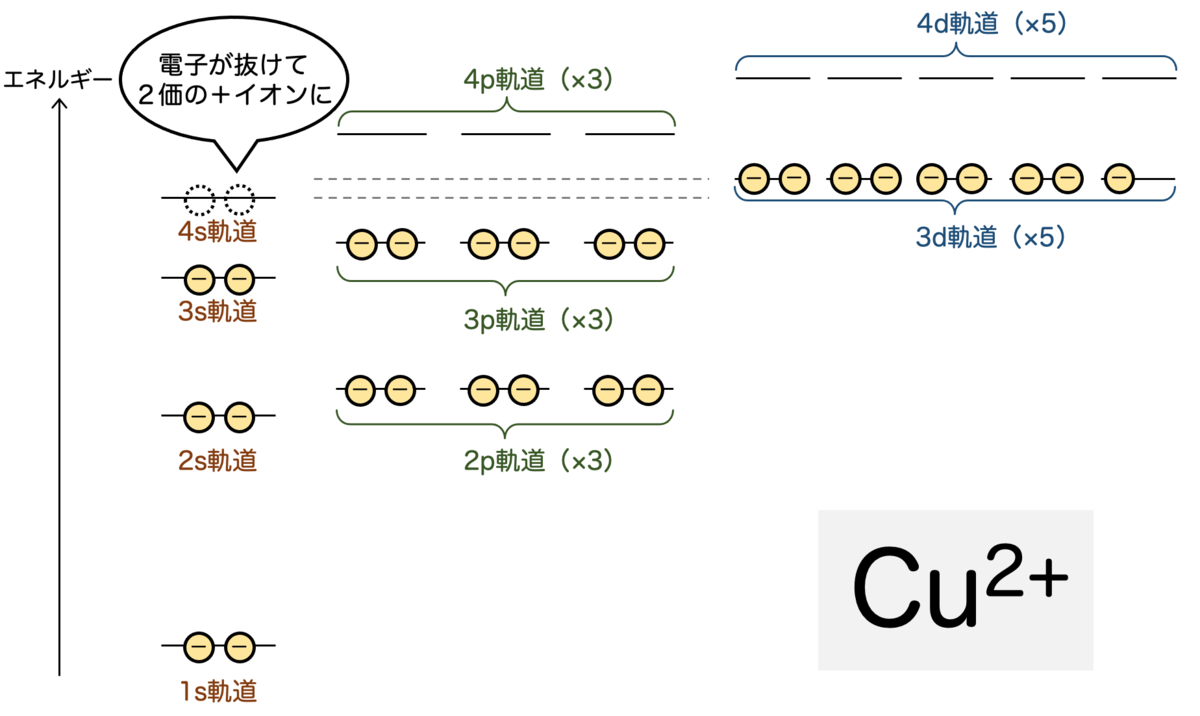
配位結合の説明を思い出すと、配位子の持つ孤立電子対を、金属原子の空の軌道に差し出すことで結合を成立させるのでした。
銅イオンの場合は、正八面体配位(つまり6個の配位子)が結合しますので、空の軌道が6つ必要 です。実際、図のような軌道が結合に使われると考えられます:
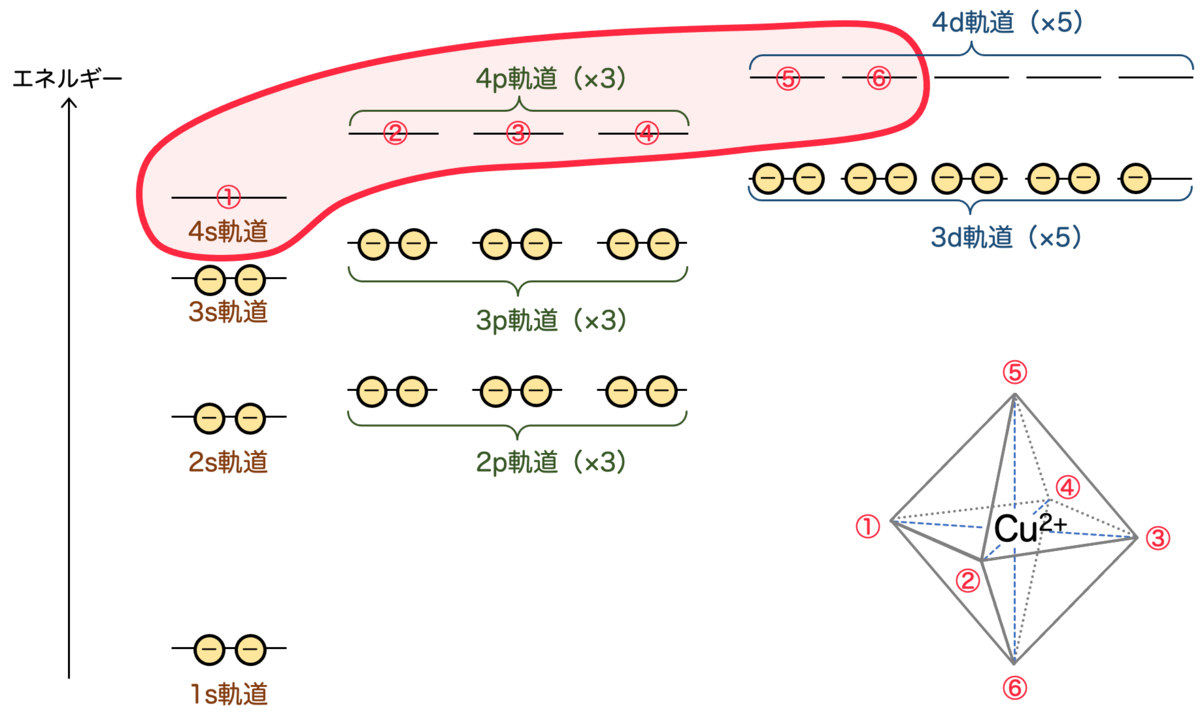
銅イオンになったことで空きが生じた4s軌道 ×1 と、4p軌道 ×3、4d軌道 ×2 の計6個ですね。
しかしながら、これらの軌道はエネルギーが異なり、対等ではありません。八面体状に配位していることを説明するために 混成軌道 という考え方を導入します。
4s軌道 ×1()と、4p軌道 ×3(
)、4d軌道 ×2(
)を、(仮に)すべて同じエネルギーを持つ軌道だと考えて、その線形結合
を考えます。このような関数の中から、改めて基底を6つ取り出してきたものが 混成軌道 です。
混成軌道として、6つの軌道が対称的になるように選べば、八面体配位することが説明できるわけですね。エネルギーはどれも等しいので、エネルギー図としては次のようになります:
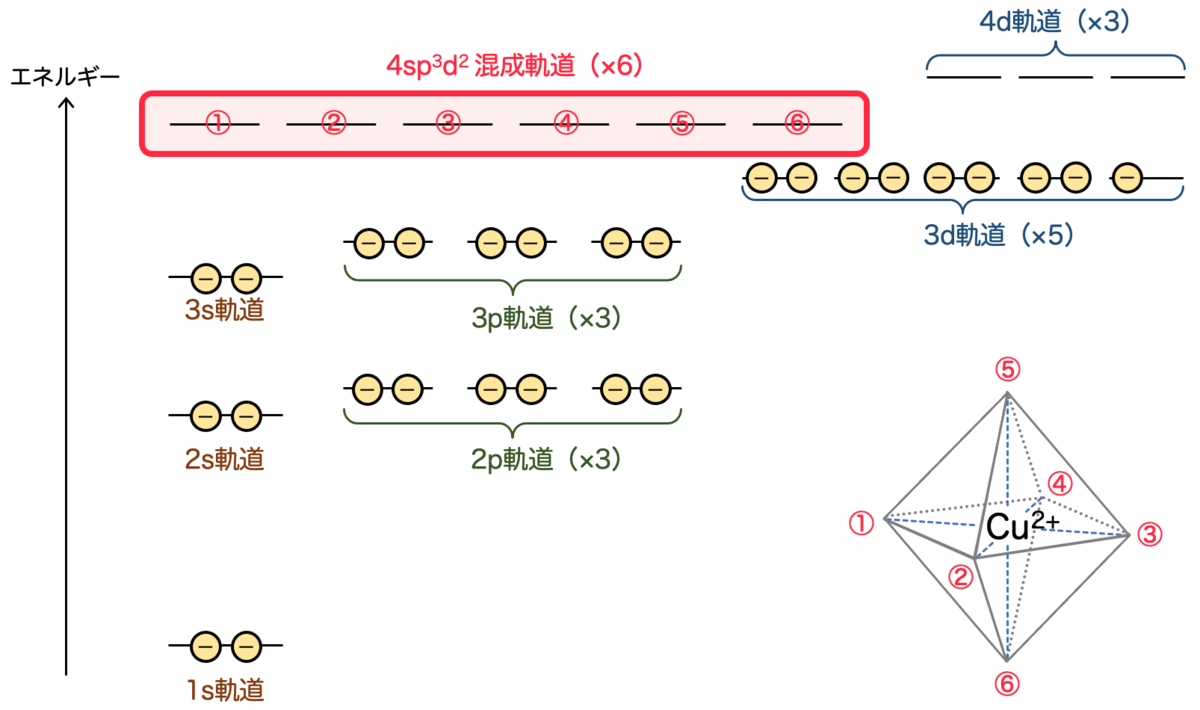
混成軌道は、あくまで分子の構造を説明するために導入された、便宜上の概念だと思った方が良さそうに思います。
6. d軌道と結晶場理論
これでひとまず、銅イオンを中心に6方向に配位子が並ぶことを説明できました。
今までの話は、主量子数 の軌道に
混成軌道6つが形成され、それらの軌道に配位子が電子を供給するということでした。
これから考えたいのは、その内側にある 3d軌道 についてです。いいですか、先ほど議論した配位結合に使った4d軌道ではなく、その内側の3d軌道が主役です。
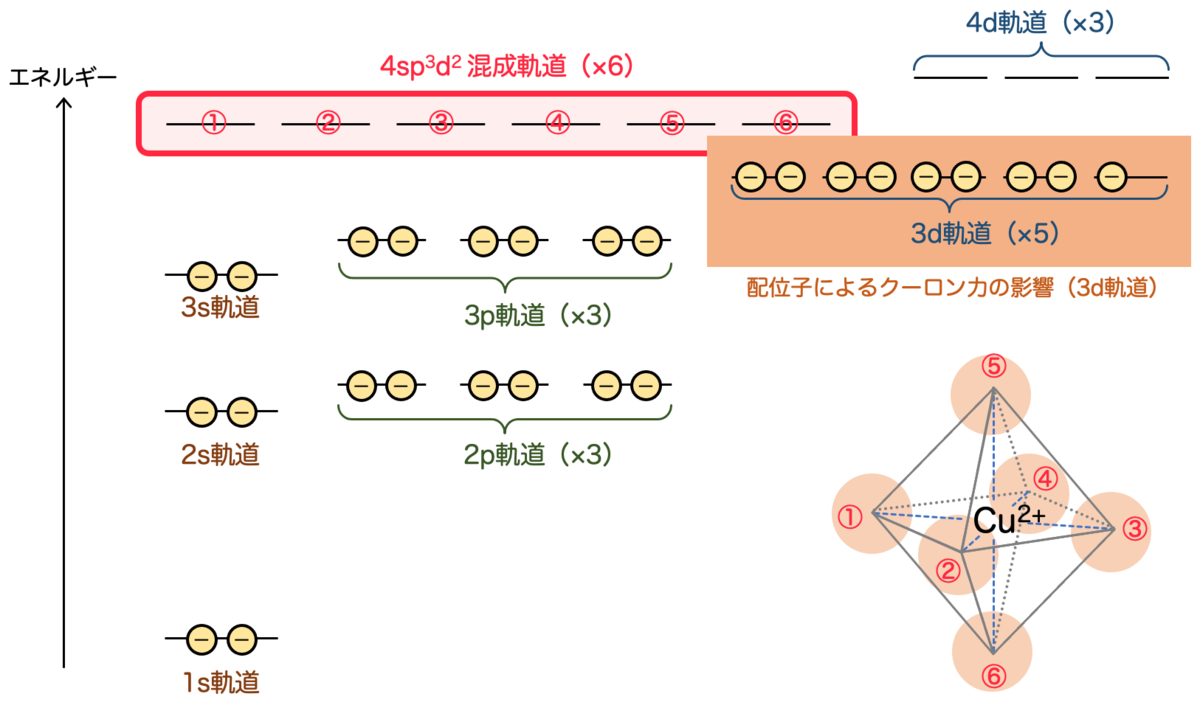
これが配位子によって影響を受ける状況について考えてみたいと思います。
まず、水素様原子でd軌道を計算したときのことを思い出しましょう。周りに何もない空間を「自由空間」といいますが、銅イオンが自由空間に置かれている状況を考えると、そのハミルトニアンは
のように書けるのでした。ここで はポテンシャルで、今の場合、原子核からのクーロン力によるポテンシャルを表します。
このハミルトニアンに対応するシュレーディンガー方程式は
ですが、これを解くと軌道が計算できるわけですね。
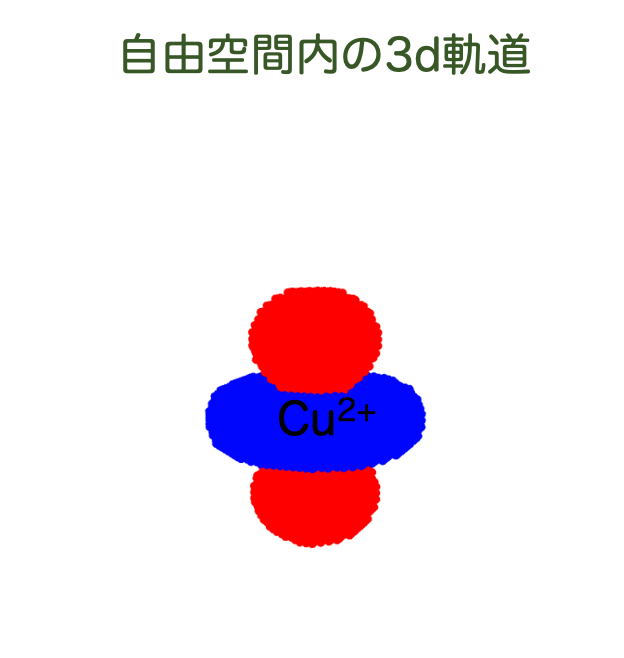
では、配位子がいる状況はどうでしょうか。
配位子は電子を持っていますので、当然クーロン力が働きます。配位子によるクーロンポテンシャルを とすると、これを考慮したハミルトニアンは
となります。このハミルトニアンに対するシュレーディンガー方程式
の解 を求めればよいわけです。
このように配位子の影響を静電場と考えて、錯体における配位子の影響を説明する理論を 結晶場理論(crystal field theory) というそうです。
ただし、この方程式も直接解くことは難しいので、近似が必要になります。
ここで配位子によるポテンシャル は、銅原子核からのポテンシャル
と比べて十分小さいと考えます。そうすると、
の方も、自由空間の軌道
に少し項を加えた形で表せるだろうと考えるわけです。
これは 摂動論 という、物理でよく用いられる常套手段です。
具体的に計算できればもちろん色々わかるのですが、計算をしなくても定性的にであれば配位子の影響を推測することが可能です。
上で説明したのは、自由空間のd軌道の形に対して、配位子の影響により軌道の形が少しだけ変化するということでした。ここで重要になるのは、d軌道の「形」によって配位子の影響の出方が異なる ということです。つまり、形を見ればある程度影響の仕方はわかるというわけです。
以下でより詳しく説明しましょう。
3d軌道には、 の5つがあるのでした。(添字に
のような意味深な記号がついていますが、これについては後編で説明します。)
それぞれの軌道は次のような形をしています:

d軌道は軌道によってかなり形が違うわけですね。これを正八面体の結晶内に置いてみると、配位子からの影響がよく分かります。たとえば、 を置いてみると、こうなります:
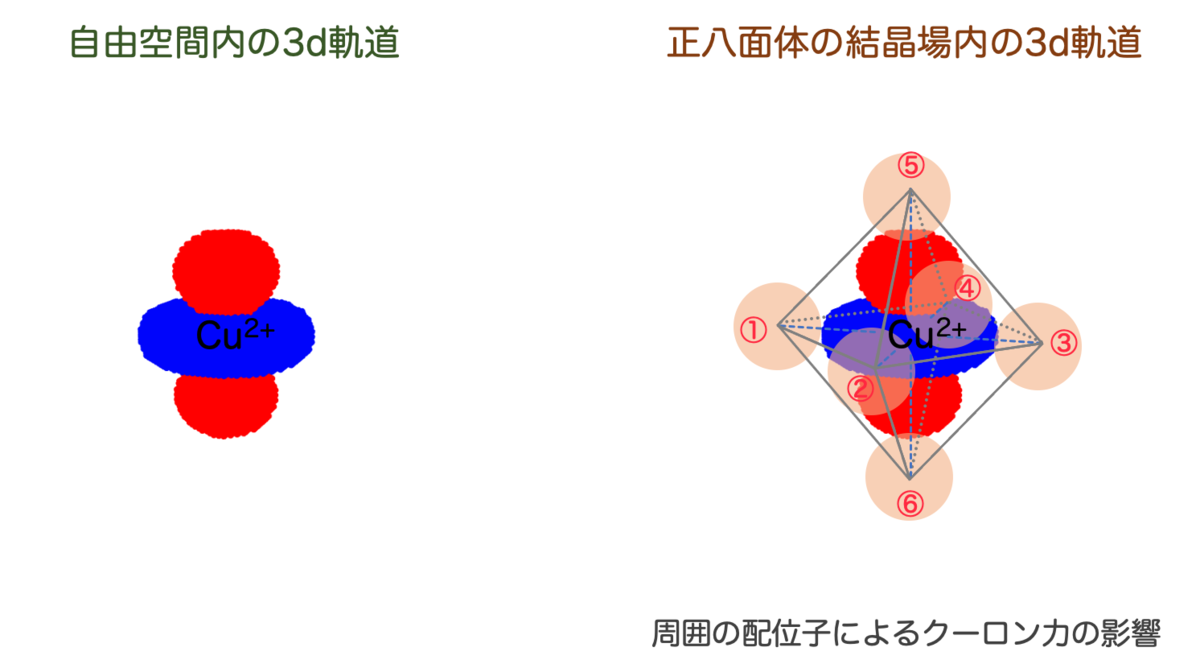
はz軸方向に張り出していますので、⑤と⑥の配位子の影響を受けそうです。
5つの軌道をすべて図示すると、その違いがよくわかります:

は⑤と⑥の影響を、
は①〜④の影響をそれぞれ強く受けそうな形をしています。
一方、 の3つについては、ちょうど配位子同士の「すきま」に電子の分布が入りこむような位置関係になっており、配位子の影響は左側2つと比べると小さそうです。
以上の観察により、 というグループと
というグループの間には、配位子が軌道に与える影響が大きく異なりそうだとわかりました。
元々、自由空間においてはd軌道のエネルギーには違いがなく、全て同じでした。つまり縮退していました。
一方、正八面体配置の配位子が付くことにより、軌道の形に応じてd軌道に対する配位子の影響に違いが生じるのです。この違いはエネルギーの違いにも現れます。
配位子の影響が強い のグループの方が、相対的にエネルギーが高くなります。つまり 縮退が解ける というわけです。
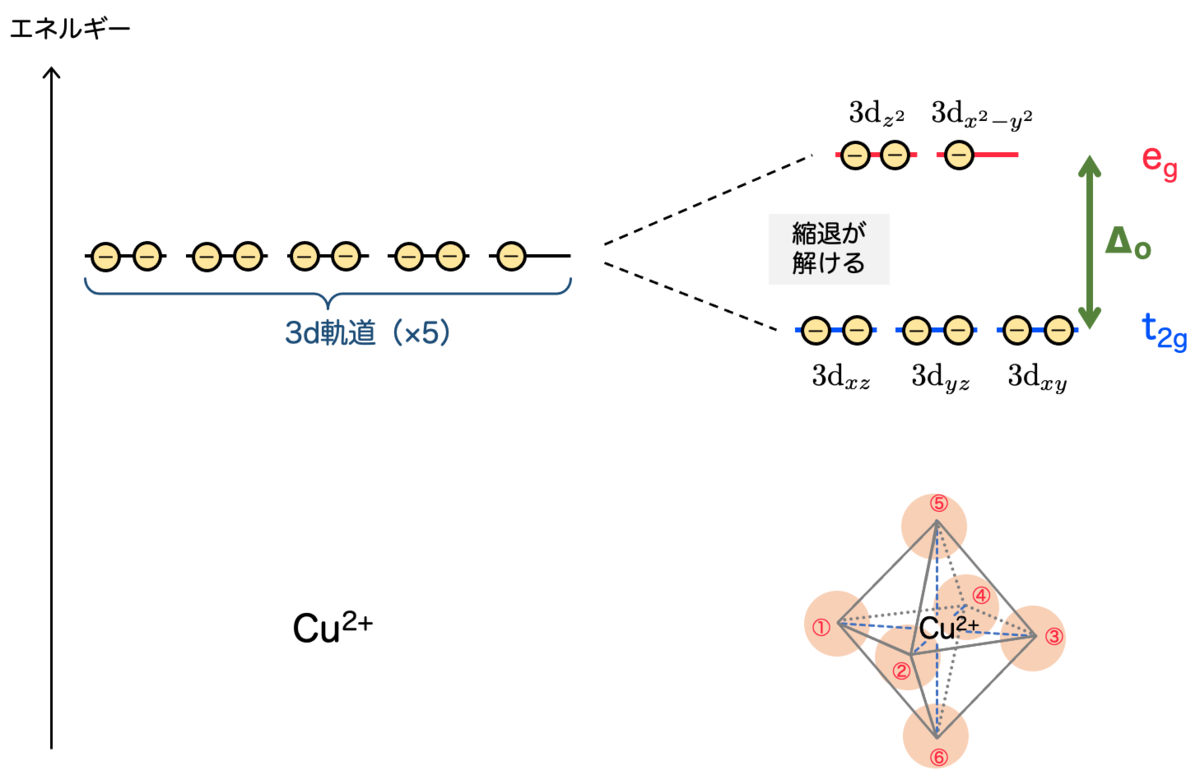
のエネルギーを
、
のエネルギーを
とすると、エネルギーが2つに分かれたことでエネルギー差
が生まれます。
d軌道の9個の電子はエネルギーが低い方から入ると考えると、基底状態では の軌道に1個分の空きが生まれます。
にいる電子は、外から
に相当する波長の光を受け取ると、吸収して
に励起します。光が吸収されるというわけですね。
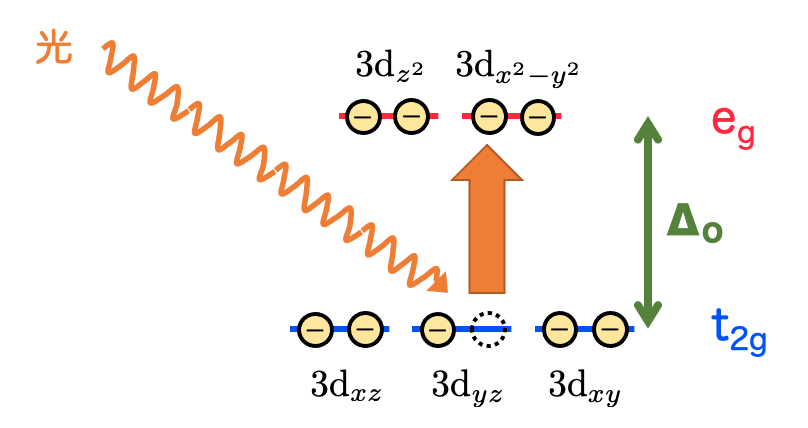
このエネルギー差に対応する波長がちょうど緑〜赤にかけての領域になるので、その補色として 青色 に見えます。これが銅(Ⅱ)イオンの錯体が青色に見える仕組みというわけです!
面白いですね!!
7. 正八面体にならない理由:ヤーン・テラー効果
前節では、銅のまわりに 正八面体状に配位していると仮定 して、配位子の影響を受けて3d軌道の縮退が解けて2つのエネルギーに分かれることを説明しました。
しかし実際の銅(Ⅱ)錯体は、正八面体そのものではなく、正八面体をz軸方向に引き伸ばした形をしているのでした。
そもそも、なぜz軸方向に引き伸ばされるのかということを説明するのが ヤーン・テラー効果 です。簡単に原理を説明します。
銅原子は3d軌道に 9個 の電子を持っています。
正八面体配位において (
のグループ)と
(
のグループ)に分かれ、
に6個の電子が入り、残り3個が
に入るわけですね。
ここで、 の縮退している2つの軌道においては、電子3個は以下の2通りのいずれかの入り方をします。

このような状況においては、一般に 「対称性を崩すことによって縮退を解く」 ように働くそうで、これにより分子の構造が変化するというのがヤーン・テラー効果です。
正八面体の場合は、①z軸方向に引き伸ばされるか、②xy平面が引き伸ばされるか、のいずれかが考えられます。銅の場合は①が起きるそうです。
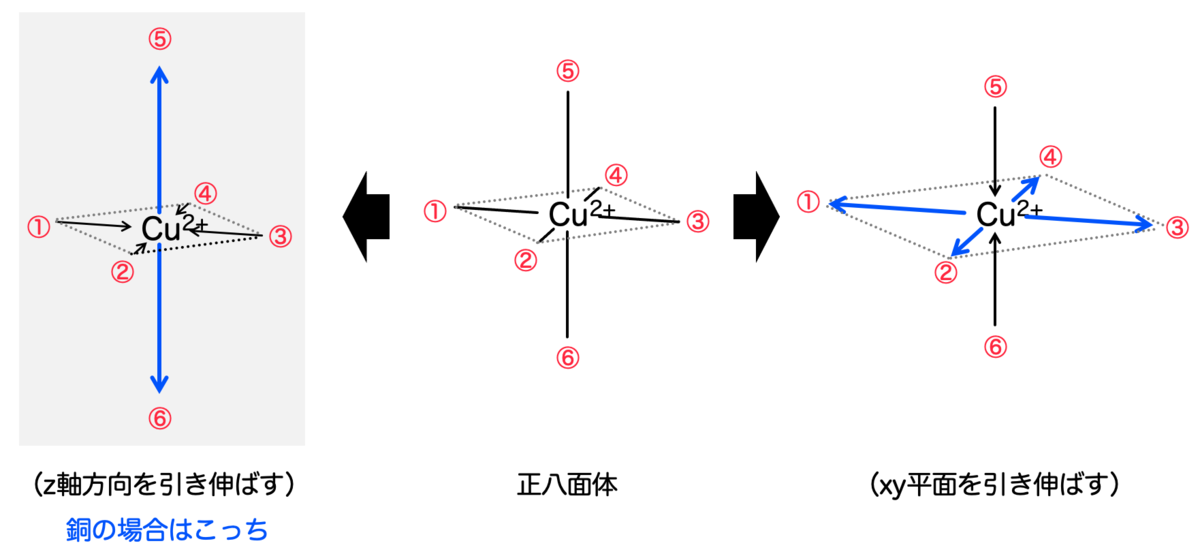
単にz軸で引き伸ばされるだけでなく、相対的にxy平面が縮んでいます。
ヤーン・テラー効果を考慮すると、エネルギーにどのような変化があるか考えてみましょう。
においては、⑤⑥の配位子が遠ざかるので影響が小さくなりエネルギーは安定化します。一方、
の方は、①〜④の配位子が近づいたことによりエネルギーは不安定化します。したがって、両者の間にエネルギー差が生まれ、縮退が解けます。

は①〜④の配位子が近づくので不安定化します。一方、
についてはやや安定化します。安定化は同程度です。したがって、
と
に分かれます。

以上をまとめると、次のような図が得られます:
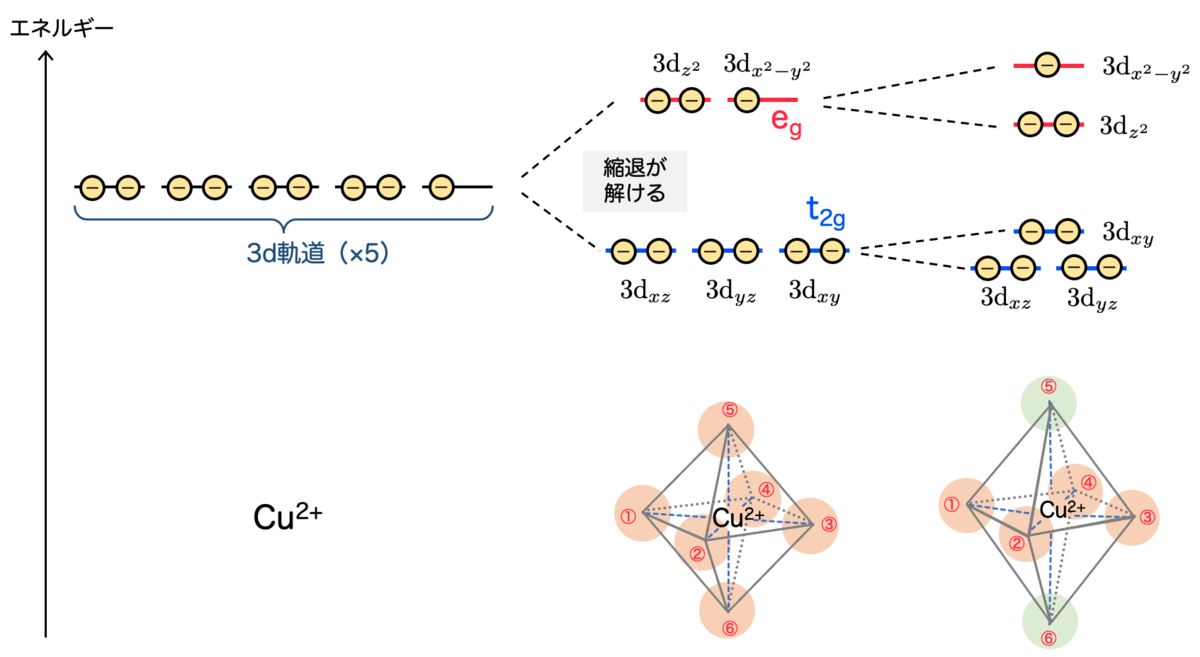
全体のエネルギーを考えると、 の方は縮退が解けたことによるエネルギーの差は小さく、また軌道がすべて埋まっているので正味のエネルギー差はありません。一方、
の方は、安定化と不安定化の程度は同程度なので、電子1個分エネルギーが安定化します。
したがって、全体のエネルギーという観点でも、対称性を崩した方が安定化するというわけですね。
8. ここまでのまとめと次回予告
今回は、硫酸銅に水を加えて得られる金属錯体が、どうして青色になるのかという問題を考えました。
銅イオンの自由空間における原子軌道を考えただけでは青色になる理由は説明できませんでした。(青色の補色の色を吸収するようなエネルギー差が存在しない。)
青色になる原因は、配位子の影響だったというわけです。配位子の静電場が、銅イオンの3d軌道に影響を与え、これにより5つの軌道の縮退が解けるという現象が起きます。縮退が解けた後の軌道のエネルギー差が、ちょうど青色の補色に対応していて、結果的に青色に見えるということでした。
大変面白いですね!
今回は、配位子の影響で縮退が解けるということを、あくまで「直感的に」説明しました。どのように分離するかについては、まだ十分な説明はできていません。
これについては、実は分子の対称性を考えることで理解できるのですが、ここで群論が使われるのです。
後編では、配位子の影響を群論を使って分析する方法について解説したいと思います。大変面白い話なので、ぜひお楽しみに!!
後編の記事はこちら:
tsujimotter.hatenablog.com
参考文献
冒頭に書いた通り、今回の記事を書くきっかけとなった記事はこちらです。
www.kiriya-chem.co.jp
今回の記事の前後編を書くにあたって、以下の教科書を参考にしました。
特に、点群自体の解説(後編)や、点群が結晶場理論にどのように関係するのかという部分(後編)については「分子軌道法」を参考にしました。
その他、参考にした記事です。



