日曜化学：量子力学の基本と球面調和関数の可視化（Python/matplotlib）

最近、とある興味 *1 から量子力学（とりわけ量子化学）の勉強をしています。

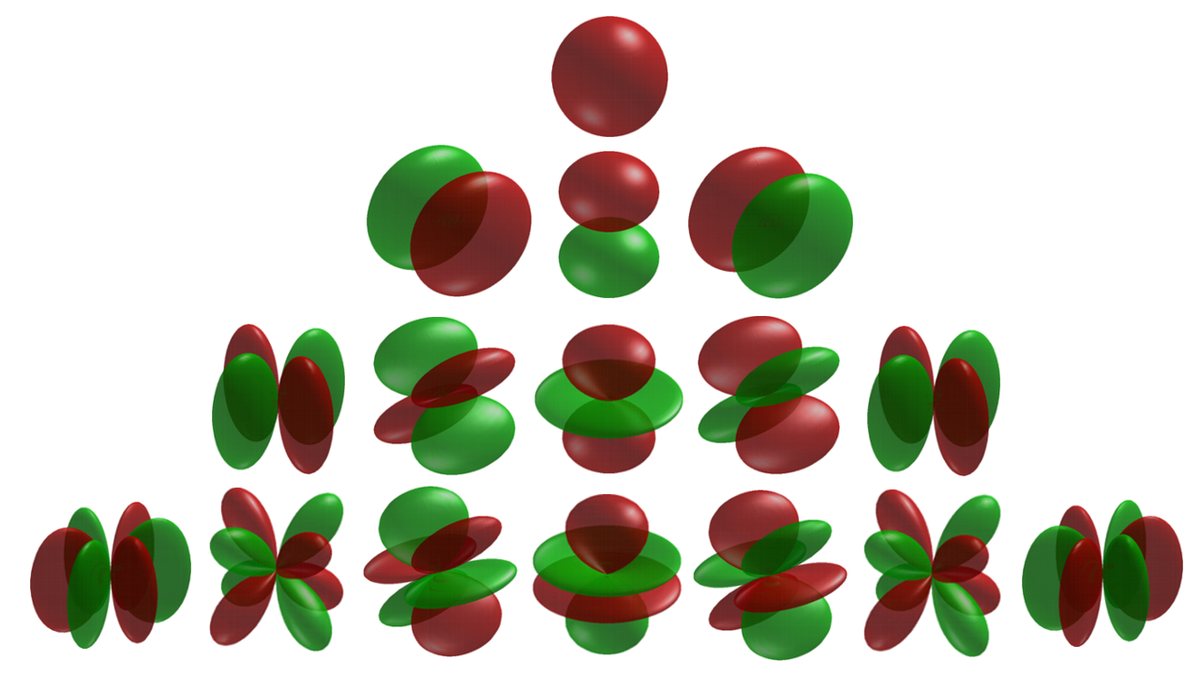
水素原子の電子の軌道を計算すると、s軌道とかp軌道とかd軌道とかの計算が載っていて、対応する図が教科書に載っていたりしますよね。

こういうやつです：

f:id:tsujimotter:20210627223229p:plain:w400

Wikipedia「球面調和関数」より引用
Attribution: I, Sarxos

個人的な体験ですが、予備校の頃は先生の影響で「化学」に大ハマりしていました *2。

ここから「Emanの物理学」というサイトの影響で「物理」に目覚め、そこからなぜか「数学」に目覚めて現在に至ります。そういった経緯もあって、化学には大変思い入れがあります。

特にこの水素原子の軌道の図は当時から気になっていて、自分で描いてみたいと思っていました。先日ようやく理解でき、実際に自分で描画できるまでになりました。以下がその画像です：

f:id:tsujimotter:20210627222555j:plain:w560

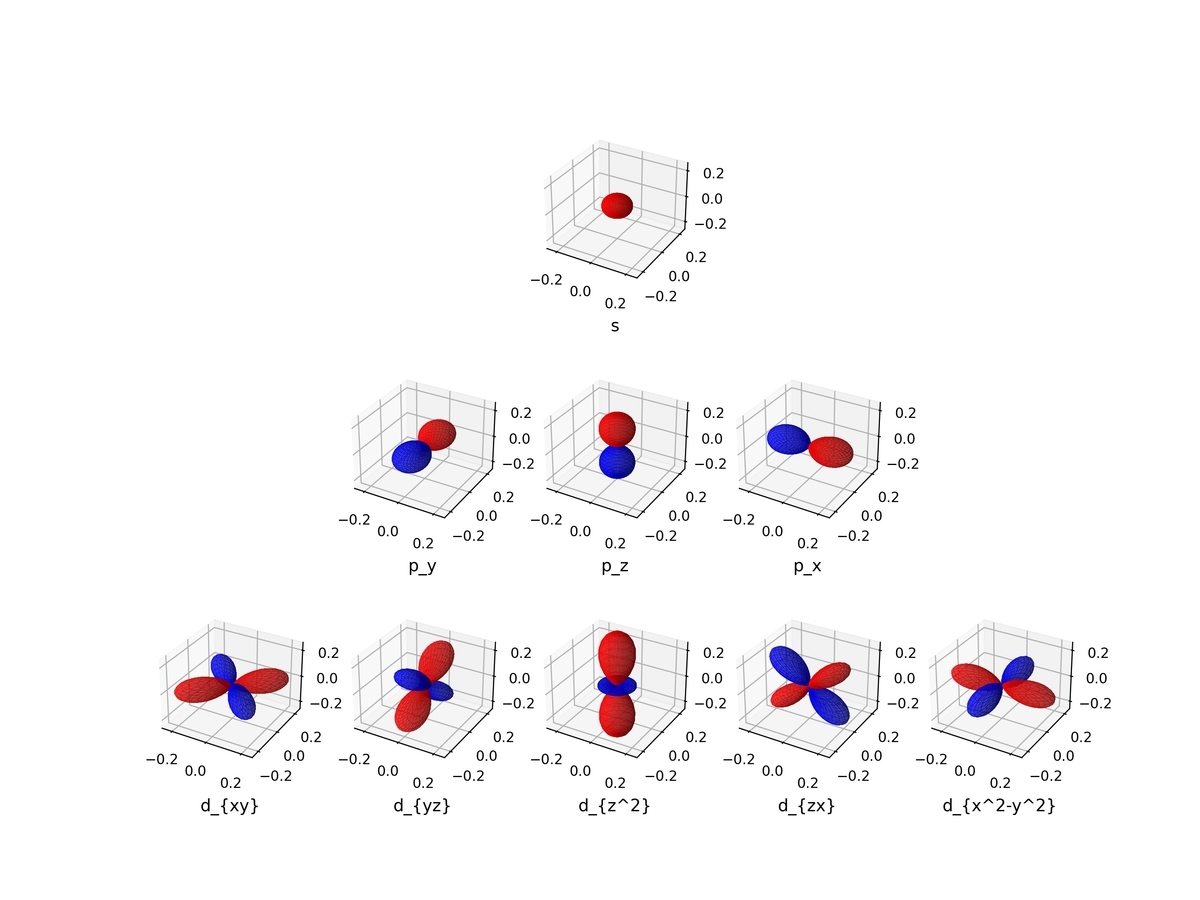
これはタイトルにもある「球面調和関数」と呼ばれる関数を可視化したものになっているのですが、この図を描くのは私の中でとても感動的な体験でした。

そこで今回の記事では上記の図の描き方を、実際に使ったプログラムを合わせて紹介したいと思います。図を描くにあたって私の中で新しく理解したことも多々ありましたので、そのノウハウも紹介したいと思います。

目次：

目次

1. 球面調和関数って？

シュレーディンガー方程式と波動関数

水素原子のシュレーディンガー方程式

変数分離

2. 変数分離した式を解く

方位角 φ についての方程式 (12) を解く

極角 θ についての方程式 (11) を解く

動径 r についての方程式 (8) を解く

3. 水素原子の原子軌道

4. 球面調和関数の可視化

l = 0 のとき（s軌道）

l = 1 のとき（p軌道）

l = 2 のとき（d軌道）

5. Pythonのmatplotlibを使ったプログラム

続きの記事はこちら

参考文献

今回の内容を理解するには量子力学に関する前提知識が必要です。

そこでセクション1〜3では、球面調和関数の背景として量子力学の基本的なところをざっとおさらいしたいと思います。その上で、水素原子のシュレーディンガー方程式の解として、球面調和関数 $Y_{l, m}(\theta, \phi)$ が現れることを紹介します。少し長くなりますので、既に内容をご存知の方は、セクション1〜3については適宜飛ばしていただいて問題ありません。

セクション4では、Pythonのmatplotlibを使って球面調和関数を実際に描画した様子を紹介します。一般に、球面調和関数は「複素関数」となってしまうので、「実関数」によって表示することが一般的で、その方法についても議論しています。

記事の一番最後のセクション5では、実際にプロットに使用したプログラムを紹介します。自分で書いてみたい方は活用していただければと思います。

1. 球面調和関数って？

ここでは、球面調和関数の背景として量子力学の基本的なところをざっとおさらいしたいと思います。

このセクションでは、水素原子のシュレーディンガー方程式を解くモチベーションの解説と、水素原子のシュレーディンガー方程式を解くことで今回の主役である球面調和関数が現れることを説明したいと思います。

シュレーディンガー方程式と波動関数

化学は、物質同士の化学反応を扱う学問です。実際の物質同士の反応の原因は、突き詰めていくとミクロな粒子（特に電子）同士の相互作用に還元されます。したがって、こうしたミクロな世界の挙動を統一的に扱う法則が必要になるわけです。

ミクロな世界においては、我々のサイズで行われる物理法則がそのまま適用できるわけではありません。ミクロな世界の粒子が従うのは「量子力学」です。

シュレーディンガー方程式 *3

$\hat{H} \Psi = E \Psi \tag{1}$

とは、そんなミクロな世界を司る基本方程式です。電子などのミクロな物質の状態を表す波動関数 $\Psi$ があり、それが満たす条件を表した方程式となっています。これを解くと電子の状態がわかるわけですね。

式 $(1)$ の右辺にある $E$ はエネルギーを表す実数であり、左辺の $\hat{H}$ はハミルトニアンという線形演算子になっています。式の形だけに着目すると、波動関数にハミルトニアンという線形作用素を作用させると、波動関数が $E$ 倍されるという形式となっています。

この形はどこかで見たことがあるのではないでしょうか。典型的な固有値問題ですね！

波動関数 $\Psi$ は一般に多粒子の状態を表すこともありますが、ここでは特に電子1粒子の状態を表すものだと考えましょう。3次元に置かれた電子の座標を ${\bf r} = (x, y, z)$ とすると、波動関数は ${\bf r}$ の関数 $\Psi({\bf r})$ だと考えることができます。

このときハミルトニアン $\displaystyle \hat{H}$ は、次のように表されます。

$\newcommand{\d}{\partial}\displaystyle \hat{H} = -\frac{\hbar}{2m_e}\left(\frac{\d^2}{\d x^2} + \frac{\d^2}{\d y^2} + \frac{\d^2}{\d z^2} \right) + V({\bf r}) \tag{2}$

ここで、 $m_e$ は電子の質量、 $\hbar$ はディラック定数（ $\hbar = h/2\pi$ 、 $h$ はプランク定数）、 $V({\bf r})$ はポテンシャルです。

要するに

$\displaystyle -\frac{\hbar}{2m_e}\left(\frac{\d^2}{\d x^2} + \frac{\d^2}{\d y^2} + \frac{\d^2}{\d z^2} \right)\Psi({\bf r}) = (E - V({\bf r}) )\Psi({\bf r}) \tag{3}$

なる方程式を解けば、電子の状態がわかるというわけですね。

特に、波動関数 $\Psi({\bf r})$ は複素数の関数ですが、絶対値の二乗 $|\Psi({\bf r})|^2$ は電子が ${\bf r}$ にいる確率密度を表します。つまり、電子が微小体積 $d{\bf r}$ 内にいる確率は $|\Psi({\bf r})|^2 \, d{\bf r}$ で表されるというわけです。

ただし、 $|\Psi({\bf r})|^2$ が確率密度であると考えるためには、これを全空間で積分した値が $1$ になっている必要があります。すなわち

$\displaystyle \int_{\text{全空間}} |\Psi({\bf r})|^2 \, d{\bf r} = 1$

が成り立つということです。

波動関数 $\Psi({\bf r})$ がこのような条件を満たすように、波動関数にあらかじめ定数をかけておくことを規格化といいます。これで波動関数の絶対値の二乗が確率密度だと解釈できるようになります。

要するに量子力学によると、電子の位置は確定せず、 $|\Psi({\bf r})|^2$ が表す確率密度に従って、空間上にぼんやりと存在するのですね。

また、ポテンシャル $V({\bf r})$ を変えれば、粒子の置かれる状況は変わるので、状況に応じてさまざまな解を取りうることになります。

水素原子のシュレーディンガー方程式

ところが現実的な問題を考えたときに、この方程式 $(3)$ を解析的に解ける状況は実はかなり限られます。

解くことができる有用な例としては、水素原子があります。水素原子は、原子核に１個の養子があり、電子が１個回っているという非常に単純な形をしています。この状況下のシュレーディンガー方程式は解析的に解くことができます。

より一般に、「水素様原子」という「正の電荷を持った原子核が１つと電子１個」の状況においても、同様に厳密に解くことができます。登場人物が２個までだったら解けるというわけですね。

もっと一般的に、登場人物が３個以上の状況、たとえば電子が複数ある状況や、原子核が複数ある場合（分子の場合）を考えたくなりますが、そういう状況ではもはや複雑すぎて厳密に解くことができないわけです。

「なんだ、量子力学はその程度のことしかわからないのか」とがっかりするかもしれませんが、そうではありません。厳密には解けなくとも、近似的に応用上有用な結果を得ることもできます。

たとえば、厳密に解ける波動関数を使って、複数の原子核によって構成される分子の軌道を近似的に表すことができたりします。これを分子軌道法といいます。この方法では、厳密解として水素原子の解を用いることになります。分子軌道法については、いつかご紹介したいと思っています。

そういった意味でも、水素原子のケースで解くことは「単なる解ける一例」ということに留まらず、重要な意味を持つわけですね。

とはいえ、この水素原子のシュレーディンガー方程式、解くのはまったく簡単ではありません。今回のテーマである球面調和関数は、この水素原子の解を表すのに用いられるので、少し解き方を理解しておくことは重要です。

まず、水素原子は原子核１個と電子１個によって構成されます。原子核を原点におき、電子の位置（座標ベクトル）を ${\bf r} = (x, y, z)$ で表します。

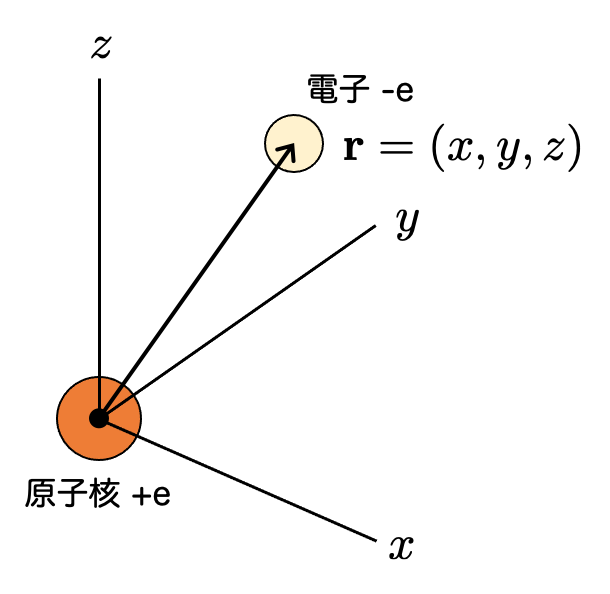
f:id:tsujimotter:20210628002856p:plain:w220

電子には、原子核との間のクーロン力が掛かっており、そのポテンシャルは原子核からの距離に反比例します。

$\displaystyle V({\bf r}) = - \frac{a}{|{\bf r}|}$

このポテンシャルは、単純に原点からの距離に依存します。このような条件では、デカルト座標系 $(x, y, z)$ を用いるよりも、球面座標系 $(r, \theta, \phi)$ で表す方が多いです。

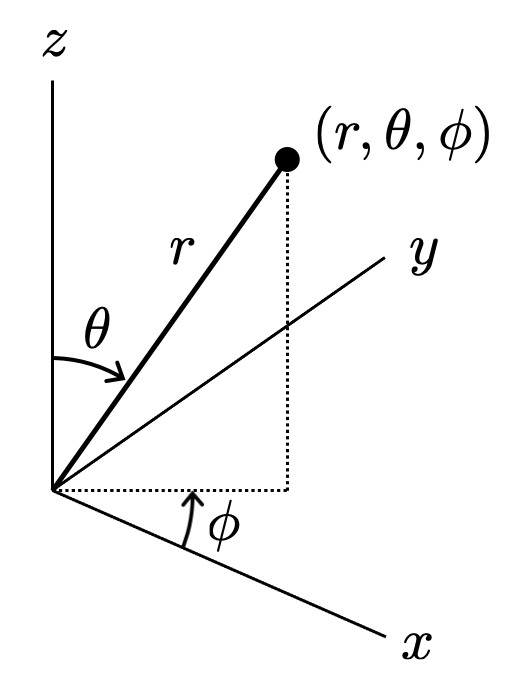
f:id:tsujimotter:20210628002203p:plain:w160

球面座標系がイメージしにくい方は、地球上の緯度・経度を思い浮かべるといいかもしれません。

$r$ は地球の半径を表す $r \geq 0$
$\theta$ は緯度（北緯・南緯）を表す $0 \leq \theta \leq \pi$
$\phi$ は経度（東経・西経）を表す $0 \leq \phi \leq 2\pi$

そこで、シュレーディンガー方程式を球面座標系 $(r, \theta, \phi)$ によって表すことにします。座標が陽に現れるのはハミルトニアンの部分なので、ここを書き換えることになります。

実際、シュレーディンガー方程式全体は、偏微分の変数変換を用いて次のように書き換えることができます：

$\displaystyle \begin{align} &-\frac{\hbar}{2m_e}\left\{\frac{1}{r^2}\frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) + \frac{1}{r^2\sin\theta}\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right) + \frac{1}{r^2\sin^2\theta}\frac{\d^2}{\d \phi^2} \right\}\Psi(r, \theta, \phi) \\ &= (E - V(r) )\Psi(r, \theta, \phi) \end{align} \tag{4}$

おいおい、どんだけ複雑な方程式を解かせるのかと思うかもしれませんが、これで問題ありません。

変数分離

以下、実際に方程式 $(4)$ を解いていくことにします。細かい式変形が続きますが、この節と次の節はだいたい雰囲気がわかれば十分です。

方程式を解くにあたって特に重要なテクニックが変数分離です。波動関数は $(r, \theta, \phi)$ の3変数関数ですが、これを $r$ の関数と $(\theta, \phi)$ の関数の積だと考えるのです。

$\Psi(r, \theta, \phi) = R(r) Y(\theta, \phi) \tag{5}$

この式を元の方程式に代入することで、「 $r$ だけを変数に持つ方程式」と「 $\theta, \phi$ だけを変数に持つ方程式」に分離することができるのです。これが変数分離です。

実際、式 $(4)$ に代入すると

$\displaystyle \begin{align} &Y(\theta, \phi)\frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) R(r) + R(r) \frac{1}{\sin\theta}\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right)Y(\theta, \phi) + R(r)\frac{1}{\sin^2\theta}\frac{\d^2}{\d \phi^2} Y(\theta, \phi) \\ &= -\frac{2m_e r^2}{\hbar}(E - V(r) )R(r)Y(\theta, \phi) \end{align} \tag{6}$

となります。 $R(r) Y(\theta, \phi)$ で割って少し整理すると

$\require{color} \newcommand{\bbr}{\textcolor{#993300}{r}}\newcommand{\bbtheta}{\textcolor{#336699}{\theta}}\newcommand{\bbphi}{\textcolor{#336699}{\phi}}\displaystyle \begin{align} &\frac{1}{R(\bbr)}\frac{\d}{\d \bbr}\left( \bbr^2 \frac{\d}{\d \bbr} \right) R(\bbr) + \frac{2m_e \bbr^2}{\hbar}(E - V(\bbr) ) \\ &= -\frac{1}{Y(\bbtheta, \bbphi)} \left\{ \frac{1}{\sin\bbtheta}\frac{\d}{\d \bbtheta}\left(\sin\bbtheta \frac{\d}{\d \bbtheta}\right) + \frac{1}{\sin^2\bbtheta}\frac{\d^2}{\d \bbphi^2} \right\} Y(\bbtheta, \bbphi) \end{align} \tag{7}$

となります。

面白いことに、式 $(7)$ の左辺は $\bbr$ だけの関数であり、右辺は $(\bbtheta, \bbphi)$ の関数となっています。これを任意の $r, \theta, \phi$ で両立する関数は、定数関数しかありえません。

そこで、その定数を $\lambda$ とおくと

$\displaystyle \frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) R(r) + \frac{2m_e r^2}{\hbar}(E - V(r) ) R(r) = \lambda R(r) \tag{8}$

$\displaystyle \left\{ \frac{1}{\sin\theta}\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right) + \frac{1}{\sin^2\theta}\frac{\d^2}{\d \phi^2} \right\} Y(\theta, \phi) = -\lambda Y(\theta, \phi) \tag{9}$

という２つの偏微分方程式が得られます。これで変数を $r$ と $(\theta, \phi)$ に分離できましたね。

式 $(8)$ の解 $R(r)$ を動径波動関数といい、式 $(9)$ の解 $Y(\theta, \phi)$ を球面調和関数と言います。

ようやく球面調和関数が出てきましたね！

動径波動関数 $R(r)$ の絶対値の２乗は原点（原子核の位置）からの距離 $r$ の中でどこに電子が存在しやすいかを表しており、球面調和関数 $Y(\theta, \phi)$ の絶対値の２乗は方向 $(\theta, \phi)$ のどの方向に電子が存在しやすいかを表しています。

これを掛け合わしたものが波動関数 $\Phi(r, \theta, \phi)$ であり、その絶対値の２乗が空間上の確率密度を表すわけですね。

2021.07.03修正：
上の $R(r)$ を「動径分布関数」と書いていましたが、「動径波動関数」に修正しました。
動径分布関数 $D(r)$ は半径 $r$ の球殻に電子がいる確率密度を表す関数 $D(r) = r^2 R(r)^2$ だったようです。

今回の主役は球面調和関数なので、具体的な解を得るために式 $(9)$ を解きたいと思います。

さらに変数分離して

$Y(\theta, \phi) = \Theta(\theta) \Phi(\phi) \tag{10}$

とすると式 $(9)$ は「 $\theta$ の関数＝ $\phi$ の関数」の形に変形できるので、やはり定数関数となります。これを $\nu$ とおくと

$\displaystyle \left\{ \sin\theta\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right) + \lambda \sin^2\theta \right\} \Theta(\theta) = \nu \Theta(\theta) \tag{11}$

$\displaystyle \frac{\d^2}{\d \phi^2} \Phi(\phi) = -\nu \Phi(\phi) \tag{12}$

という２つの式が得られます。

これで一通り変数分離できましたので、解くべき３つの方程式をまとめておきたいと思います。

$\displaystyle \frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) R(r) + \frac{2m_e r^2}{\hbar}(E - V(r) ) R(r) = \lambda R(r) \tag{8再掲}$

$\displaystyle \left\{ \sin\theta\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right) + \lambda \sin^2\theta \right\} \Theta(\theta) = \nu \Theta(\theta) \tag{11再掲}$

$\displaystyle \frac{\d^2}{\d \phi^2} \Phi(\phi) = -\nu \Phi(\phi) \tag{12再掲}$

2. 変数分離した式を解く

方程式を解きやすい形に分離できましたので、あとは１個ずつ解いていくことになります。

この節の内容は結構細かい計算が続きますが、その狙いは計算そのものではありません。方程式を解くに当たって、解には制約が現れ、「量子数」と呼ばれる整数が現れます。これを知ってもらいたいというのが狙いです。

方位角 φ についての方程式 (12) を解く

一番簡単に解けそうなのは式 $(12)$ です。実際

$\Phi(\phi) = A e^{\pm i \sqrt{v} \phi} \tag{13}$

の形をした関数が解となるわけですね。

ただし、ここからが大変重要なポイントなのですが、この形をした関数がすべて解となるわけではありません。今、 $\phi$ は球面座標（地球で言うところの「経度」）を表しているので、周期性があります。すなわち

$\Phi(2\pi) = \Phi(0)$

を満たす必要があるのですね。これが成立するためには、式 $(13)$ において $\pm \sqrt{\nu}$ が整数である必要があります。

したがって、整数 $m = \pm \sqrt{\nu}$ として

$\Phi(\phi) = A e^{i m \phi} \tag{14}$

という形のものが解となるわけですね。この $m$ を磁気量子数といいます。

定数を規格化しておくと（ $0\leq \phi \leq 2\pi$ で積分して $1$ になるように定数 $A$ をとる）

$\displaystyle \Phi_m(\phi) = \frac{1}{\sqrt{2\pi}} e^{i m \phi} \tag{15}$

が得られます。

つまり、今やったことを整理すると

$\displaystyle \frac{\d^2}{\d \phi^2} \Phi(\phi) = -\nu \Phi(\phi)$

が解を持つためには、 $\nu$ は整数 $m$ を用いて $\nu = m^2$ と表せる必要があり、その解は

$\displaystyle \Phi_m(\phi) = \frac{1}{\sqrt{2\pi}} e^{i m \phi}$

と表せるということですね。

もう少し突っ込んで線形代数の話をすると、上記の２解は

$\displaystyle \frac{\d^2}{\d \phi^2} \Phi(\phi) = -\nu \Phi(\phi)$

における固有値 $\nu = -m^2$ に対応する解ということになります。

同じ固有値 $\nu = -m^2$ に対する固有空間は、２次元のベクトル空間となっており、基底 $\frac{1}{\sqrt{2\pi}} e^{i m \phi}$ と $\frac{1}{\sqrt{2\pi}} e^{-i m \phi}$ を用いて線形結合

$\displaystyle \frac{C_1}{\sqrt{2\pi}} e^{i m \phi} + \frac{C_2}{\sqrt{2\pi}} e^{-i m \phi}$

として表せます。

つまり、上の式 $(13)$ の形の解は、同じ固有空間の基底を「たまたま」選んだものだということになります。本来は、線形結合すべてが解になるわけですが、その中から特別な基底を我々は選んで使っているというわけです。

基底の選び方には特に基準があるわけではないので、別の基底をとっても良いということに注意しましょう。これはあとで「実関数表示」を考えるにあたって必要なものとなります。

極角 θ についての方程式 (11) を解く

$\displaystyle \left\{ \sin\theta\frac{\d}{\d \theta}\left(\sin\theta \frac{\d}{\d \theta}\right) + \lambda \sin^2\theta \right\} \Theta(\theta) = m^2 \Theta(\theta) \tag{11再掲}$
（元の式 $(11)$ に $\nu = m^2$ を代入したものを掲載しています。）

答えを言ってしまうと、次が方程式 $(11)$ の解となります：

$\displaystyle \Theta_{l, m}(\theta) = (-1)^{\frac{m+|m|}{2}} \sqrt{\frac{2l+1}{2} \frac{(l-|m|)!}{(l+|m|)!}} \, P_l^{|m|}(\cos \theta) \tag{16}$

2021.07.03追記：
「答えを言ってしまうと」と書いてしまいましたが、私自身はこの方程式 $(11)$ の解き方を知っているわけではありません。参考文献の数式を引用しています。いつか理解できればと思っています。

かなり複雑な関数に見えるかもしれませんが、実はそこまででもないので、じっくり説明していきます。

実際、解の因子を色分けしてみると

$\displaystyle \Theta_{l, m}(\theta) = \textcolor{#dd830c}{(-1)^{\frac{m+|m|}{2}} \sqrt{\frac{2l+1}{2} \frac{(l-|m|)!}{(l+|m|)!}} } \, P_l^{|m|}(\cos \theta)$

となっていて、オレンジ色の部分は単なる係数です。（規格化のための定数となっています。）

パラメータとして $l$ が入っていますが、これはやはり式 $(11)$ が解を持つための条件を考えたときに、出てくるものです。

式 $(11)$ には $\lambda$ というパラメータがありましたが、（ $\Phi(\phi)$ のときと同様）すべての $\lambda$ で解を持つわけではありません。実は、整数 $l$ を用いて

$\lambda = l(l+1) \tag{17}$

$l \geq |m| \tag{18}$

と表せるときに限り、対応する解 $\Theta_{l, m}(\theta)$ を持つわけです。この $l$ を方位量子数といいます。

$\Theta_{l, m}(\theta)$ の本体は、実をいうと $P_{l}^{|m|}(\cos \theta)$ の部分だけです。 $P_{l}^{|m|}(x)$ はルジャンドルの陪多項式と呼ばれるもので、定義は次の通りです：

$\displaystyle P_l^{|m|}(x) = (1-x^2)^{|m|/2} \frac{d^{|m|} P_l(x)}{dx^{|m|}}$

$\displaystyle P_l(x) = \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2 - 1)^l$

これは複雑に見えますが、具体的に計算してみるとただの多項式（or そのルート）になることがわかるかと思います。

$l = 0$ のとき	$\displaystyle P_{0}^{0}(x) = 1$
$l = 1$ のとき	$\displaystyle P_{1}^{0}(x) = x$ $\displaystyle P_{1}^{1}(x) = \sqrt{1-x^2}$
$l = 2$ のとき	$\displaystyle P_{2}^{0}(x) = \frac{1}{2}(3x^2 - 1)$ $\displaystyle P_{2}^{1}(x) = 3\sqrt{1-x^2} x$ $\displaystyle P_{2}^{1}(x) = 3(1-x^2)$
$l = 3$ のとき	$\displaystyle P_{3}^{0}(x) = \frac{1}{2}(5x^3 - 3x)$ $\displaystyle P_{3}^{1}(x) = \frac{3}{2}\sqrt{1-x^2} (5x^2 - 1)$ $\displaystyle P_{3}^{2}(x) = 15(1-x^2)x$ $\displaystyle P_{3}^{3}(x) = 15\sqrt{1-x^2}(1-x^2)$

これらに $x = \cos \theta$ を代入して、 $-\pi \leq \theta \leq \pi$ で積分したときに $1$ になるように係数を決めると、上の $\Theta_{l, m}(\theta)$ が得られるわけですね。

結局、球面調和関数は、整数の組 $(l, m)$ によって $Y_{l, m}$ と表され、 $Y_{l, m}(\theta, \phi) = \Theta_{l, m}(\theta) \Phi_m(\phi)$ と表されるというわけです。

改めて書くと次のように表せます。これが球面調和関数の具体的な形です。

$\displaystyle Y_{l, m}(\theta, \phi) = (-1)^{\frac{m+|m|}{2}} \sqrt{\frac{2l+1}{4\pi} \frac{(l-|m|)!}{(l+|m|)!}} \, P_l^{|m|}(\cos \theta)\, e^{im\phi} \tag{19}$

動径 r についての方程式 (8) を解く

$\displaystyle \frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) R(r) + \frac{2m_e r^2}{\hbar}(E - V(r) ) R(r) = l(l+1) R(r) \tag{8再掲}$
（元の式 $(8)$ に $\lambda = l(l+1)$ を代入したものを掲載しています。）

動径波動関数 $R(r)$ についても同様に方程式 $(8)$ を解くことで解が得られます。

方程式 $(8)$ には、エネルギー $E$ というパラメータが入っていますが、やはりすべての $E$ に対して解を持つわけではありません。これについても、主量子数という正の整数 $n = 1, 2, 3, \ldots$ に対応する $E_n$ についてのみ解を持つことになります。 $E_n$ は具体的には

$\displaystyle E_n = -\frac{a^2 m_e}{2\hbar} \frac{1}{n^2} \tag{20}$

という形になります。電子が水素原子にいる以上は、このような形のエネルギーしか取り得ないということを意味します。

これがエネルギーが飛び飛びの値をとるの意味するところです。

f:id:tsujimotter:20210701144030p:plain:w320

また

$n \geq l + 1 \tag{21}$

という関係も成り立つ必要があります。

3. 水素原子の原子軌道

議論がかなり長かったので、一旦まとめます。

水素原子においては、方程式を解く過程で得られた整数の組（量子数） $(n, l, m)$ に対応する解（波動関数）しかとれない。順に $n$ を主量子数、 $l$ を方位量子数、 $m$ を磁気量子数という。

量子数 $(n, l, m)$ に対応する波動関数を

$\Psi_{n,l,m}(r, \theta, \phi) = R_{n, l}(r) Y_{l, m}(\theta, \phi)$

と表す。 $R_{n, l}(r)$ は動径波動関数、 $Y_{l, m}(\theta, \phi)$ は球面調和関数。

また、各量子数は次のような条件を満たす：

$n$ は正の整数（ $n = 1, 2, 3, \ldots$ ）
$l$ は $n \geq l+1$ を満たす非負整数
$m$ は $|m| \leq l$ を満たす整数（負の値もとる）

さらに、エネルギー $E_n$ は $n$ に対して次のように定まる：

$\displaystyle E_n = -\frac{a^2 m_e}{2\hbar} \frac{1}{n^2}$

したがって、エネルギーはとびとびの値をとる（これ以外の値をとることができない）。

$n = 1$ がエネルギー最小で、 $n$ が大きくなるほど、エネルギーは単調増加する。

以上を踏まえて原子軌道という概念を導入します。原子軌道は単に軌道ということもあります。

水素原子においては、方程式を解く過程で量子数と呼ばれる整数の組が得られ、これらに対応する解しかもたないのでした。すなわち、水素原子の電子の波動関数は、量子数に対応するものしかないということですね。

そこで量子数の条件から、取り得る組み合わせを考えていきましょう。 $n = 1, 2, 3$ について考えると、次のようになります：

主量子数	取り得る量子数の組
$n = 1$ のとき	$(n, l, m) = \textcolor{#663300}{(1, 0, 0)}$ の１つ
$n = 2$ のとき	$(n, l, m) = \textcolor{#663300}{(2, 0, 0)}, \textcolor{#336633}{(2, 1, -1), (2, 1, 0), (2, 1, 1)}$ の４つ
$n = 3$ のとき	$(n, l, m) = \textcolor{#663300}{(3, 0, 0)}, \textcolor{#336633}{(3, 1, -1), (3, 1, 0), (3, 1, 1)},$ $\textcolor{#003366}{(3, 2, -2), (3, 2, -1), (3, 2, 0), (3, 2, 1), (3, 2, 2)}$ の９つ

これらの量子数の組一つ一つを軌道といいます。

エネルギーは、 $n = 1$ が最小で、 $n = 2$ 、 $n = 3$ と大きくなるにつれて単調増加します。同じ主量子数の軌道においては、エネルギーはすべて等しくなります。

エネルギーの高低を踏まえて、水素原子の軌道を図示したものが次の図となります：

f:id:tsujimotter:20210701144509p:plain:w560

電子は基本的にはエネルギーが低いところに入るのがより安定となります。つまり、水素原子においては、 $(n, l, m) = (1, 0, 0)$ の状態にいるのが最も安定というわけですね。このような状態（もっとも安定な状態）のことを基底状態と言います。

逆に、基底状態よりもエネルギーが高い状態のことを励起状態といいます。たとえば、電子に電磁波が当たると、電磁波からエネルギーを受け取って励起状態に移ることがあります。このとき、取りうるエネルギーは $E_1, E_2, E_3, \ldots$ のいずれかしかとれません。したがって、エネルギーの差がちょうど電磁波のエネルギーに一致するものしか吸収されないのです。

電磁波のエネルギーは $h \nu$ （ $\nu$ は振動数）と表されるので、ちょうど振動数がぴったり一致するものしか吸収できないことが帰結されます。これは実験的事実とも合致します。

今は水素原子そのものを考えていますが、ポテンシャル $V(r) = -\frac{a}{r}$ の $a$ の部分を適当に変えれば、原子の個数を増やした原子核を作ることができます。つまり、原子核の電荷が $+Z$ であるような原子における電子 $1$ 個の挙動を考えることができるわけですね。これが「水素様原子」です。これもまったく同じ軌道を有することになります。

さらに踏み込んで、電子をもっと増やしてみましょう。「電子を一つ一つ増やしていってもあまり状況は変わらないと仮定する」と、任意の原子の状況を再現できそうです。

２個目の電子ももっとも安定な $(n, l, m) = (0, 0, 0)$ という軌道に入ります。

では、３個目はというと、実は $(n, l, m) = (1, 0, 0)$ に入ります。面白いことにもっとも安定なはずの $(n, l, m) = (0, 0, 0)$ には入らないのです。いったいどういうことでしょう？

この背景には、パウリの排他律という原理があります。

パウリの排他律：電子は同じ軌道に２つまでしか入ることができない

各軌道に対しては、それぞれ２つずつの状態があると考えることができます。これはスピンと呼ばれる、これまで説明しなかった第４の量子数が関係しています。

ここでは詳しく説明できませんが、電子には軌道の他にスピンという状態（上向きと下向きの２種類）があり、同じ軌道・同じスピンの状態をとることができないのです。

このように、軌道が埋まれば電子は上のエネルギーの軌道に入っていきます。同じ主量子数であれば、水素原子においては同じエネルギーでしたが、電子が増えるにつれて少しずつずれが生じてきます。多電子原子のエネルギーはおよそ次のようになります。

f:id:tsujimotter:20210701144735p:plain:w560

ところで、原子軌道にはもう少し馴染み深い表現がありますので、紹介します。

主量子数 $n = 1$ の１つの軌道：K殻
主量子数 $n = 2$ の４つの軌道：L殻
主量子数 $n = 3$ の９つの軌道：M殻

まさに高校化学で習った用語ですね！　各軌道には２個ずつの電子が入ることになるので、「K殻・L殻・M殻にそれぞれ２個・８個・１８個の電子が入る」ということになります。高校化学で習ったのは、こういうことだったわけですね。

さらに、方位量子数 $l$ に対しても、次のような名前がついています：

$l = 0$ のとき：s軌道
$l = 1$ のとき：p軌道
$l = 2$ のとき：d軌道

特に、主量子数に対応して次の表のような呼び方をします：

	$l = 0$	$l = 1$	$l = 2$
$n = 1$ （K殻）	1s軌道	ー	ー
$n = 2$ （L殻）	2s軌道	2p軌道	ー
$n = 3$ （M殻）	3s軌道	3p軌道	3d軌道

エネルギーの図では、このようになります：

f:id:tsujimotter:20210701145037p:plain:w560

4. 球面調和関数の可視化

さて、ここまでで一通りの前提が説明し終わりました。少し長かったですがお疲れ様でした。

ここからが本題なのですが、原子軌道 $(n, l, m)$ に対応する波動関数 $\Psi_{n,l,m}(r, \theta, \phi)$ を可視化したいと思います。

しかしながら、波動関数 $\Psi_{n,l,m}$ は3次元空間の点 $(r, \theta, \phi)$ に対して複素数を返す関数なので、かなり可視化するのが難しいものです。

そこで、 $r$ のことは一回忘れて「どの方向 $(\theta, \phi)$ に対して電子が多く分布しているのか」だけを考えたいと思います。ちょうど、波動関数 $\Psi_{n,l,m}$ は

$\Psi_{n,l,m}(r, \theta, \phi) = R_{n,l}(r) Y_{l,m}(\theta, \phi)$

のように変数分離されており、 $r$ を定数だと思えば $R_{n,l}(r)$ は一回忘れてしまっても良さそうです。

そこで、球面調和関数 $Y_{l,m}(\theta, \phi)$ を可視化しようという発想になるわけです。「どっちの方向に電子が多く分布するのか」ということなので、電子の分布の形をおおよそ捉えることにも繋がるわけですね。こっちの方向に電子が偏っているので反応しやすそうだ、みたいなことがわかるわけです。

また、波動関数の絶対値の２乗は確率密度を表すのでした。したがって、各 $l, m$ について

$|Y_{l,m}(\theta, \phi)|^2$

をプロットしてみたら良さそうですね。

実際にプロットするにあたっては

$r(\theta, \phi) = |Y_{l,m}(\theta, \phi)|^2$

として、 $|Y_{l,m}|^2$ の値が大きいほど原点からの距離 $r$ が遠いところに点がプロットされるように描いてみましょう。

イメージがなかなか難しいと思うので、以下では具体的に描いてみましょう。この記事の最後にPythonのプログラムを載せましたので、自分で確認したい方はぜひご活用ください。
（以下の説明に使う図は、すべて同じプログラムで作成されています。）

l = 0 のとき（s軌道）

このときは、 $m = 0$ しかとりませんので

$r(\theta, \phi) = |Y_{0,0}(\theta, \phi)|^2$

をプロットしてみましょう。

球面調和関数を計算すると

$\displaystyle Y_{0,0}(\theta, \phi) = \frac{1}{\sqrt{4\pi}}$

となります。ずいぶんシンプルになりましたね。

よって

$\displaystyle r(\theta, \phi) = \frac{1}{4\pi}$

ということになります。

右辺は角度に依存しませんので、どちらの方向も偏りなく電子が分布していることになります。原点からの距離が一定値 $\frac{1}{4\pi}$ をとるわけですから、球面ということになりますね。

実際、プロットするとこうなります：

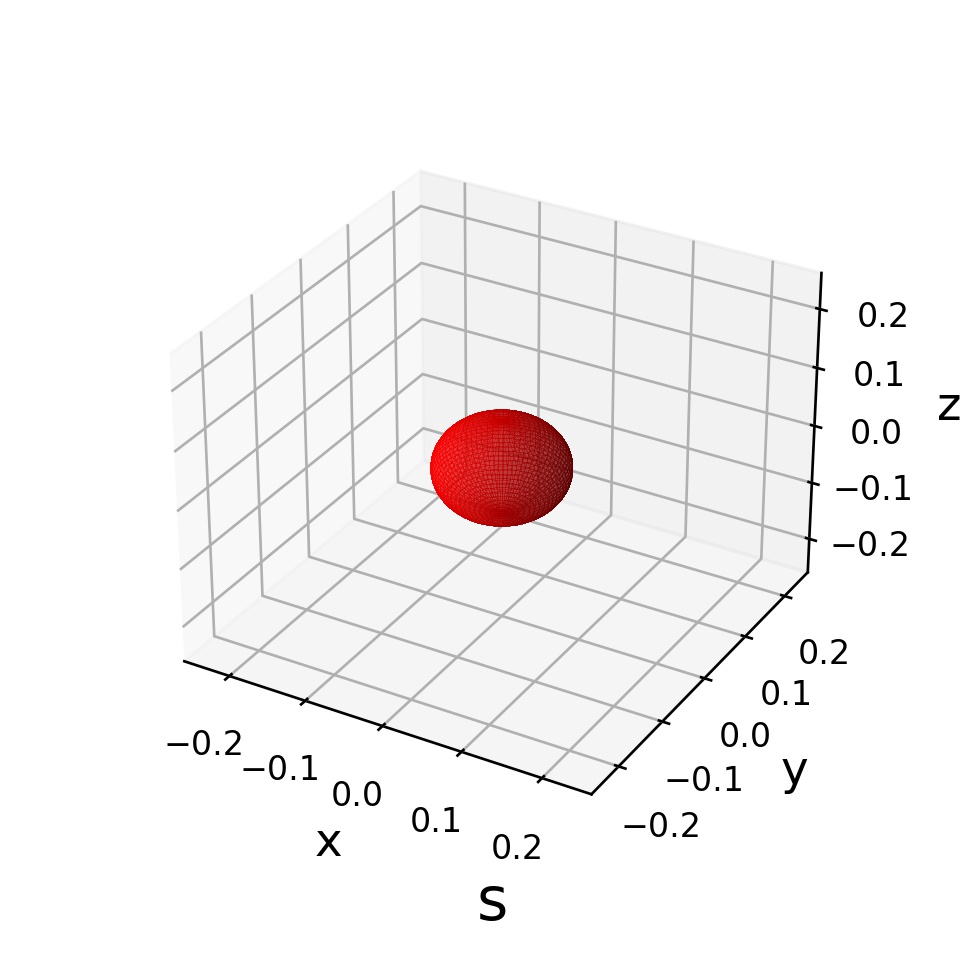
f:id:tsujimotter:20210627222139j:plain:w280

これがs軌道の電子の分布の形状ということになります。勘違いしてはいけないのは、電子が図で表した球面上に張り付いているというわけではないということです。

この図はあくまで「どの方向に電子が多く分布しているのか」を表す図であるからです。原点からの距離には「（角度に対する）相対的な強度の違い」以上の意味はありません。

実際、空間上のどの位置に電子が分布しているのかどうかは、動径波動関数 $R(r)$ との積によって決まってきます。

l = 1 のとき（p軌道）

$l = 1$ のときは、p軌道というのでした。このとき、 $m = -1, 0, +1$ の３つの軌道が存在します。

$m = 0$ のときは比較的簡単です。具体的に代入すると

$\displaystyle Y_{1,0}(\theta, \phi) = \sqrt{\frac{3}{4\pi}} \cos\theta$

となることがわかります。絶対値の２乗をとって

$\displaystyle r(\theta) = |Y_{1,0}(\theta, \phi)|^2 = \frac{3}{4\pi} \cos^2\theta$

を考えることになります。

右辺には $\phi$ がないので、 $\phi$ の方向（地球でいうと「経度」）については同じ値をとります。（図形としては回転体）

$0\leq \theta \leq \pi$ に対して $\cos^2 \theta$ となるわけですが、 $\cos^2(0) = 1, \;\; \cos^2(\pi/2) = 0, \;\; \cos^2(\pi) = 1$ なので「一回凹んでまた戻る」ような図になるはずです。

実際、描画してみるとこうなります：

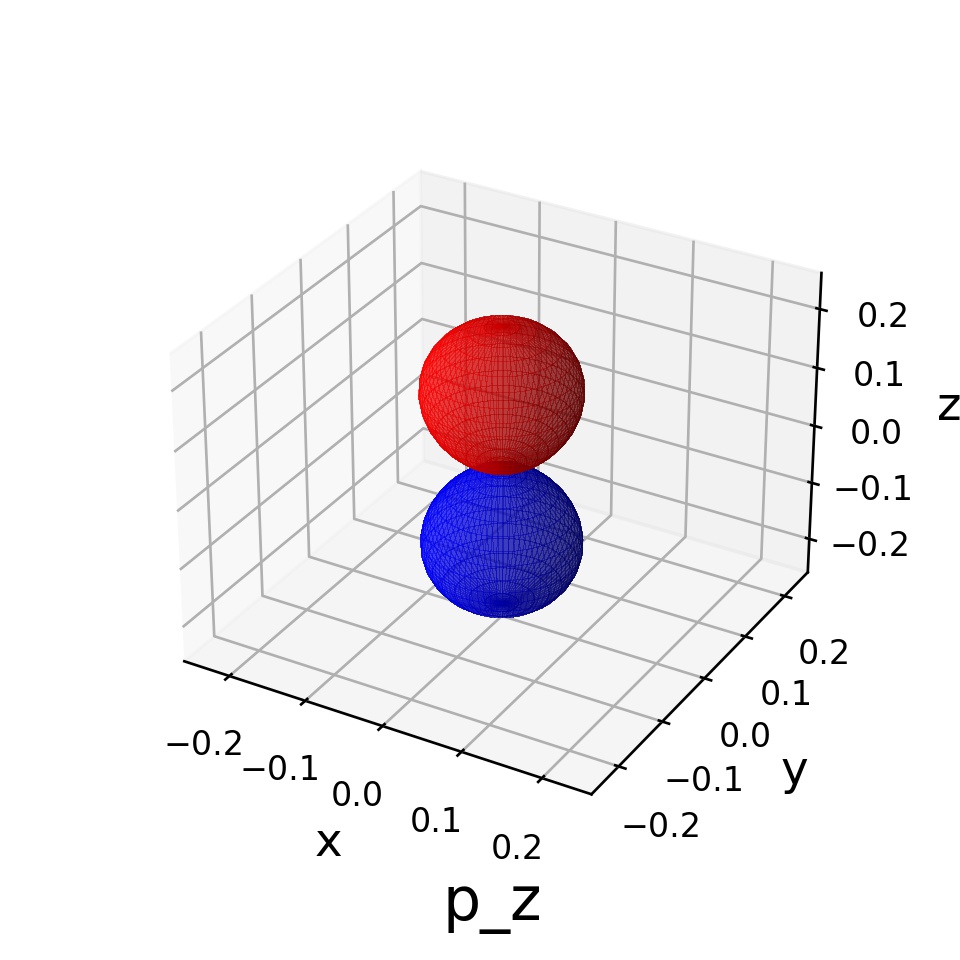
f:id:tsujimotter:20210627222122j:plain:w280

予想した通りになっているのではないでしょうか。 $z$ 軸方向にでっぱった「マラカス」みたいな形状ができています。これを $p_z$ 軌道ということにします。

赤と青の２色で色分けされていますが、これは絶対値を取る前の関数 $Y_{1, 0}(\theta, \phi)$ の正負によって分けしています（正の領域は「赤」、負の領域は「青」）。今回は直接関係ありませんが、今後分子軌道を考える上では符号の正負は関係あります。

問題は $m = -1$ と $m = 1$ についてです。マラカスを $x$ 軸方向・ $y$ 軸方向に倒したような形状が期待されますが、そのままではそうなりません。

先ほど得られた解に $l = 1, \;\; m = \pm 1$ を代入すると

$\displaystyle Y_{1, -1}(\theta, \phi) = \sqrt{\frac{3}{8\pi}} \sin\theta \, e^{-i\phi} \tag{22}$

$\displaystyle Y_{1, 1}(\theta, \phi) = -\sqrt{\frac{3}{8\pi}} \sin\theta \, e^{i\phi} \tag{23}$

となります。これらの絶対値をとると、どちらも同じ関数になってしまいます。

絶対値の二乗 $r = |Y_{1, \pm 1}(\theta, \phi)|^2$ を上に書いた方法でプロットすると、こうなります：

f:id:tsujimotter:20210628014019j:plain:w280

トーラスのような形状になりました。想定していた図とはちょっと違う感じになりますね。

冒頭で紹介したような図は、「実関数表示」というのを考えたものになります。

$\Phi_m(\phi)$ を計算したときのことを思い出しましょう。式 $(22), (23)$ において $\Phi_m(\phi)$ に対応する部分は

$\displaystyle \Phi_{1}(\phi) = \frac{1}{\sqrt{2\pi}} e^{i\phi}$

$\displaystyle \Phi_{-1}(\phi) = \frac{1}{\sqrt{2\pi}} e^{-i\phi}$

になります。これらは固有方程式

$\displaystyle \frac{\d^2}{\d \phi^2} \Phi(\phi) = - \Phi(\phi)$

の解です。これは固有値 $-1$ に対応する固有空間の基底として、「たまたま」上の１組を選んだものとなっています。固有空間の中から基底はどのように選んでもよいわけです。

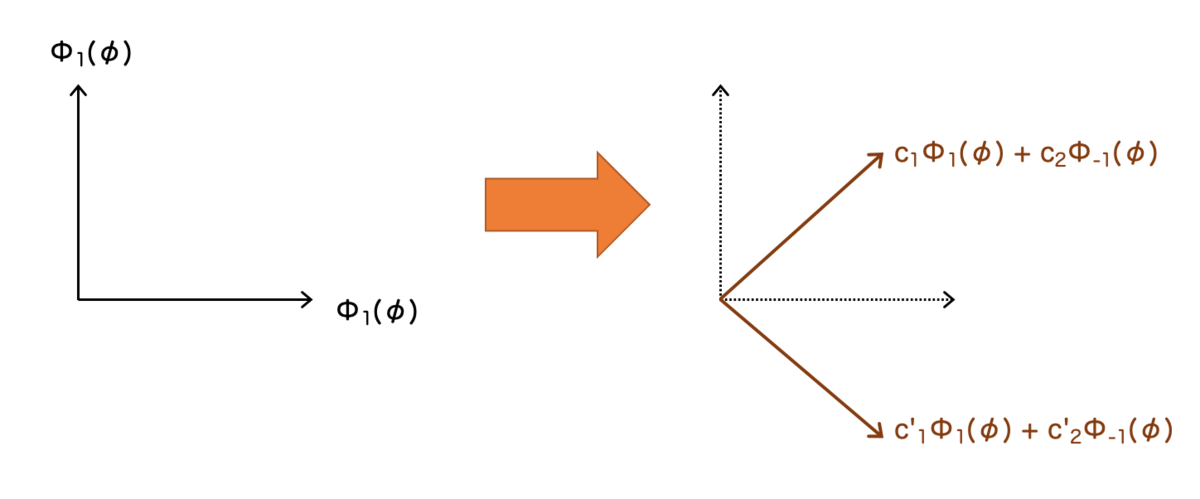
f:id:tsujimotter:20210628014800p:plain:w460

異なる基底をとるイメージ

これを踏まえて、球面調和関数の線形結合

$\displaystyle \frac{1}{\sqrt{2}}( Y_{1, -1}(\theta, \phi) - Y_{1, 1}(\theta, \phi) )$

$\displaystyle -\frac{1}{\sqrt{2}i}( Y_{1, -1}(\theta, \phi) + Y_{1, 1}(\theta, \phi) )$

を基底として採用することにしましょう。

計算すると

$\displaystyle \frac{1}{\sqrt{2}}( Y_{1, -1}(\theta, \phi) - Y_{1, 1}(\theta, \phi) ) = \sqrt{\frac{3}{4\pi}} \sin\theta \, \frac{e^{i\phi} + e^{-i\phi}}{2} = \sqrt{\frac{3}{4\pi}} \sin\theta \, \cos\phi \tag{24}$

$\displaystyle -\frac{1}{\sqrt{2}i}( Y_{1, -1}(\theta, \phi) + Y_{1, 1}(\theta, \phi) ) = \sqrt{\frac{3}{4\pi}} \sin\theta \, \frac{e^{i\phi} - e^{-i\phi}}{2i} = \sqrt{\frac{3}{4\pi}} \sin\theta \, \sin\phi \tag{25}$

となります。

元々の表示 $(22), (23)$ が複素関数だったのに対し、式 $(24), (25)$ では実関数となっています。基底関数が実関数で表せるわけですから、これは嬉しいですね。式 $(24), (25)$ のことを実関数表示と呼びます。

というわけで、実関数表示した球面調和関数の絶対値の二乗を、これまでと同様の方法でプロットしてみましょう。

つまり

$\displaystyle r(\theta, \phi) = \left|\frac{1}{\sqrt{2}} (Y_{1, -1}(\theta, \phi) - Y_{1, 1}(\theta, \phi) ) \right|^2 = \frac{3}{4\pi} \sin^2\theta \, \cos^2\phi$

$\displaystyle r(\theta, \phi) = \left|-\frac{1}{\sqrt{2i}} (Y_{1, -1}(\theta, \phi) + Y_{1, 1}(\theta, \phi) ) \right|^2 = \frac{3}{4\pi} \sin^2\theta \, \sin^2\phi$

をプロットするわけですね。

実際にプロットしたのが次の図です：

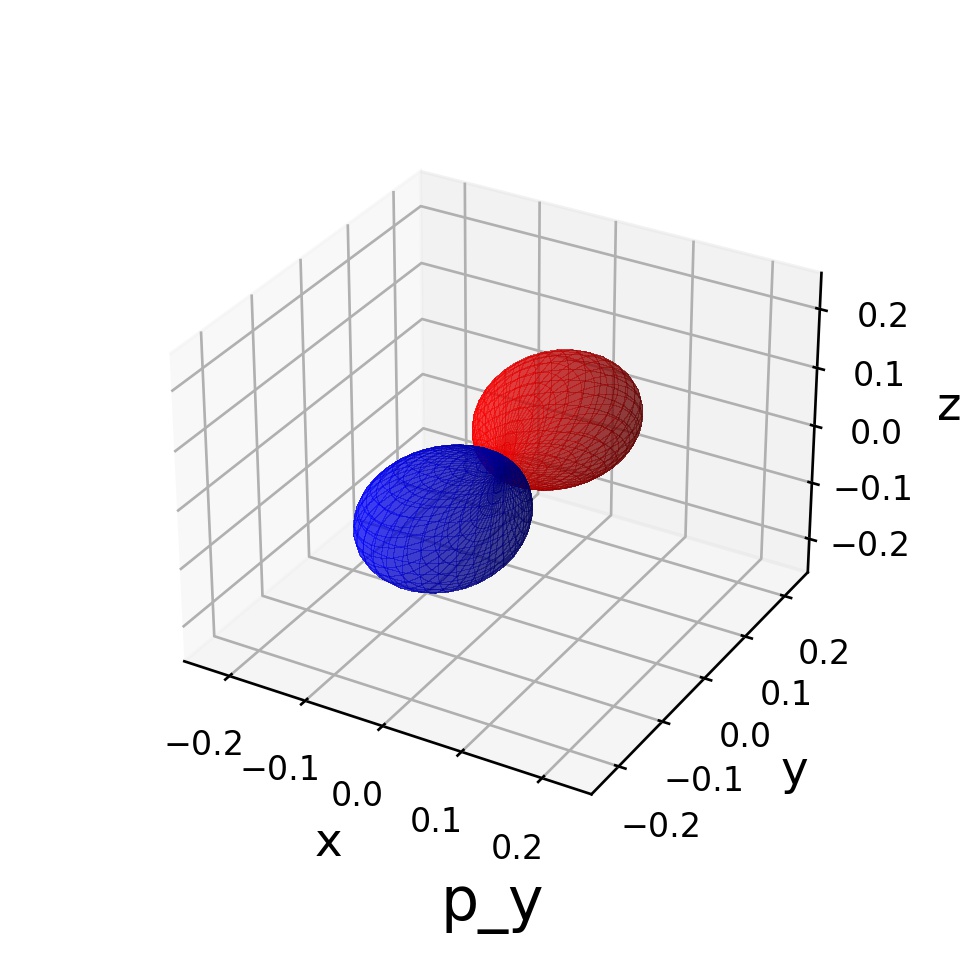
f:id:tsujimotter:20210627222235j:plain:w240

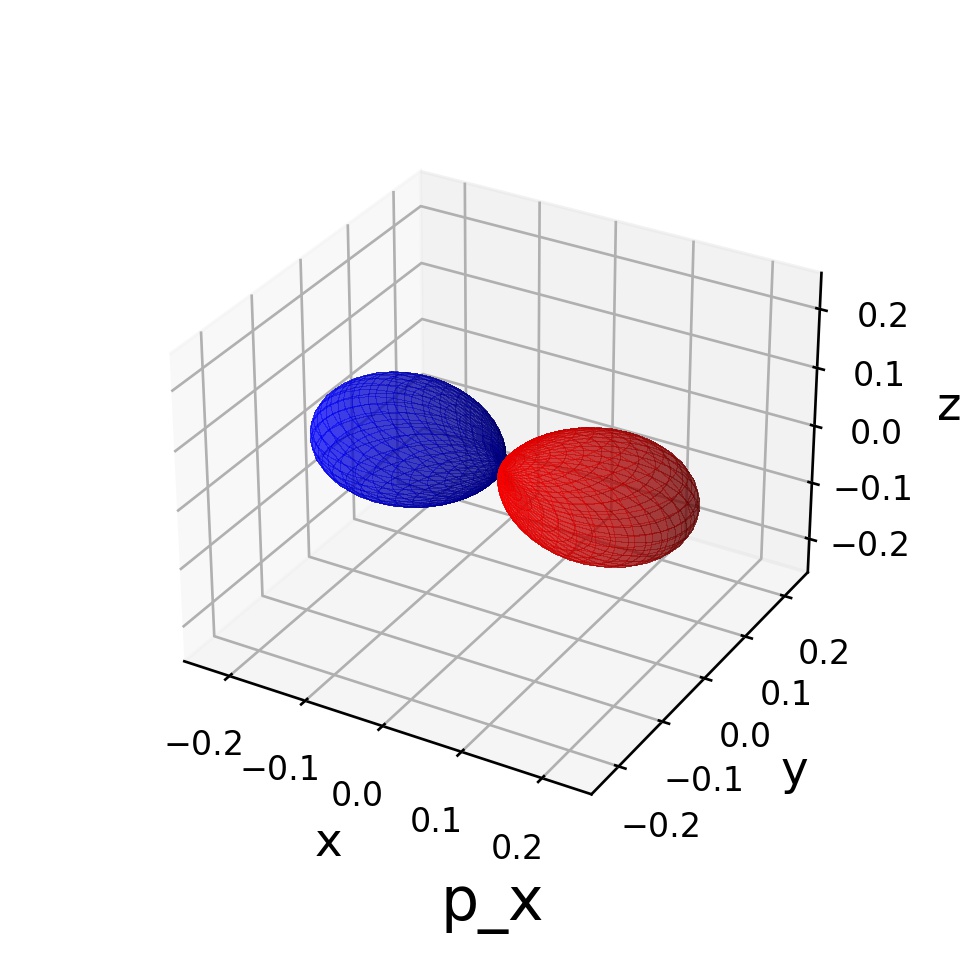
f:id:tsujimotter:20210627222250j:plain:w240

左側は $y$ 軸方向に「マラカス」みたいな形状ができていますので $p_y$ 軌道、右側は $x$ 軸方向なので $p_x$ 軌道といいます。

というわけで、よくあるp軌道の図はこのように書けるわけですね！

l = 2 のとき（d軌道）

d軌道について考えましょう。 $l = 2$ のとき、 $m = -2, -1, 0, 1, 2$ の5通りとなります。対応する球面調和関数は次の5つです。

$Y_{2, -2}(\theta, \phi) = \sqrt{\frac{15}{32\pi}} \sin^2\theta \, e^{-2i\phi}$
$Y_{2, -1}(\theta, \phi) = \sqrt{\frac{15}{8\pi}} \cos\theta \,\sin\theta \, e^{-i\phi}$
$Y_{2, 0}(\theta, \phi) = \sqrt{\frac{5}{16\pi}} (3\cos^2\theta - 1)$
$Y_{2, 1}(\theta, \phi) = -\sqrt{\frac{15}{8\pi}} \cos\theta \,\sin\theta \, e^{i\phi}$
$Y_{2, -2}(\theta, \phi) = \sqrt{\frac{15}{32\pi}} \sin^2\theta \, e^{2i\phi}$

$m \neq 0$ については複素関数となっていますので、実関数表示を考えましょう。

$m = \pm 1$ については同じ固有空間に属するので、次の線形結合を考えます：

$\displaystyle \frac{1}{\sqrt{2}}(Y_{2, -1}(\theta, \phi) - Y_{2, 1}(\theta, \phi) ) = \sqrt{\frac{15}{4\pi}} \cos\theta \,\sin\theta \, \cos\phi$

$\displaystyle -\frac{1}{\sqrt{2}i}(Y_{2, -1}(\theta, \phi) + Y_{2, 1}(\theta, \phi) ) = \sqrt{\frac{15}{4\pi}} \cos\theta \,\sin\theta \, \sin\phi$

$m = \pm 2$ についても同様に次の線形結合を考えます：

$\displaystyle \frac{1}{\sqrt{2}}( Y_{2, 2}(\theta, \phi) + Y_{2, -2}(\theta, \phi) ) = \sqrt{\frac{15}{16\pi}} \sin^2\theta \, \cos 2\phi$

$\displaystyle \frac{1}{\sqrt{2}i}( Y_{2, 2}(\theta, \phi) - Y_{2, -2}(\theta, \phi) ) = \sqrt{\frac{15}{16\pi}} \sin^2\theta \, \sin 2\phi$

そんなわけで、以下の５つの実関数表示をプロットすることになります。

$\displaystyle \frac{1}{\sqrt{2}i}( Y_{2, 2}(\theta, \phi) - Y_{2, -2}(\theta, \phi) ) = \sqrt{\frac{15}{16\pi}} \sin^2\theta \, \sin 2\phi$
$\displaystyle -\frac{1}{\sqrt{2}i}(Y_{2, -1}(\theta, \phi) + Y_{2, 1}(\theta, \phi) ) = \sqrt{\frac{15}{4\pi}} \cos\theta \,\sin\theta \, \sin\phi$
$\displaystyle Y_{2, 0}(\theta, \phi) = \sqrt{\frac{5}{16\pi}} (3\cos^2\theta - 1)$
$\displaystyle \frac{1}{\sqrt{2}}(Y_{2, -1}(\theta, \phi) - Y_{2, 1}(\theta, \phi) ) = \sqrt{\frac{15}{4\pi}} \cos\theta \,\sin\theta \, \cos\phi$
$\displaystyle \frac{1}{\sqrt{2}}( Y_{2, 2}(\theta, \phi) + Y_{2, -2}(\theta, \phi) ) = \sqrt{\frac{15}{16\pi}} \sin^2\theta \, \cos 2\phi$

これらの絶対値の二乗をとってプロットすると、次のようになります：

f:id:tsujimotter:20210627222314j:plain:w240

f:id:tsujimotter:20210627222351j:plain:w240

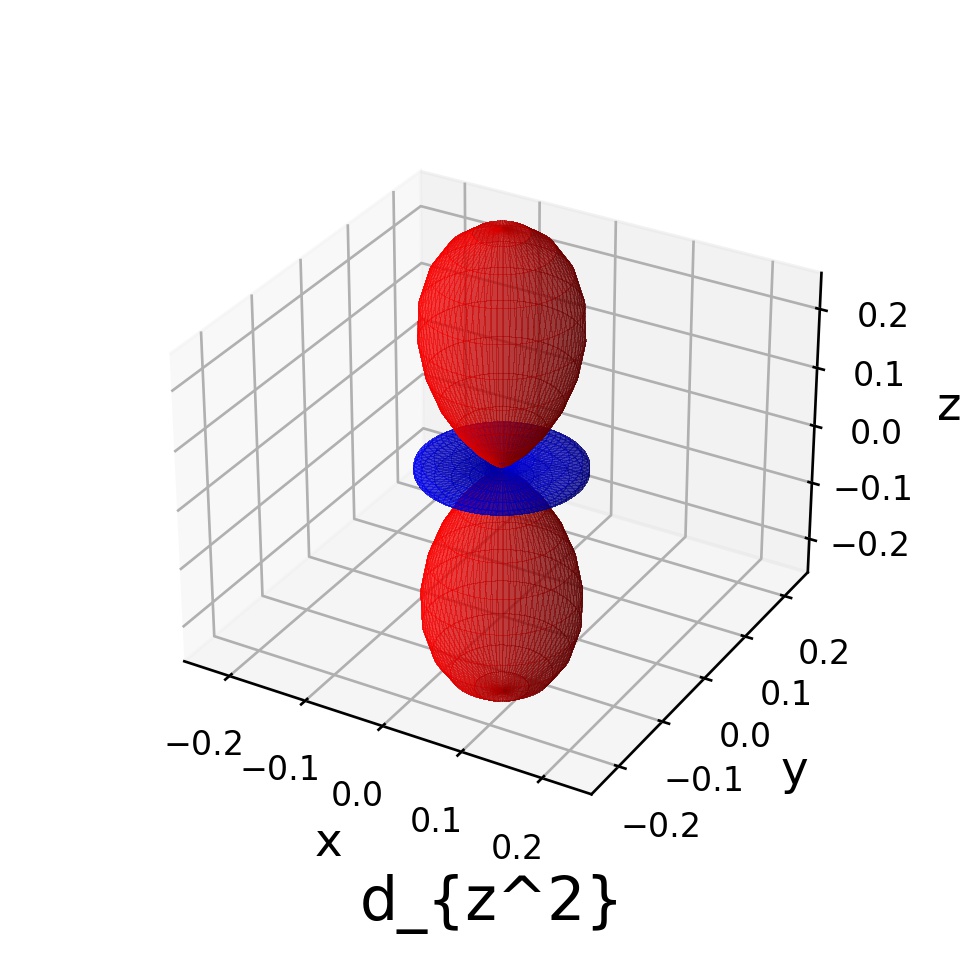
f:id:tsujimotter:20210627222408j:plain:w240

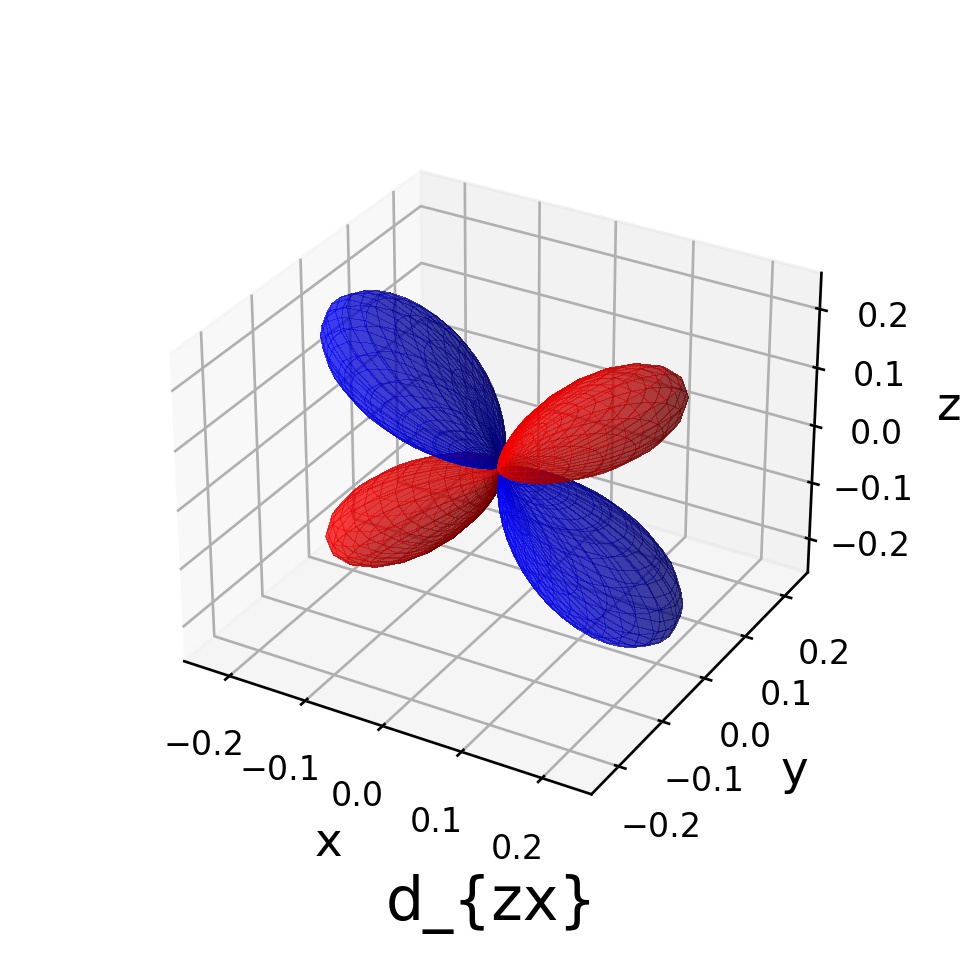
f:id:tsujimotter:20210627222430j:plain:w240

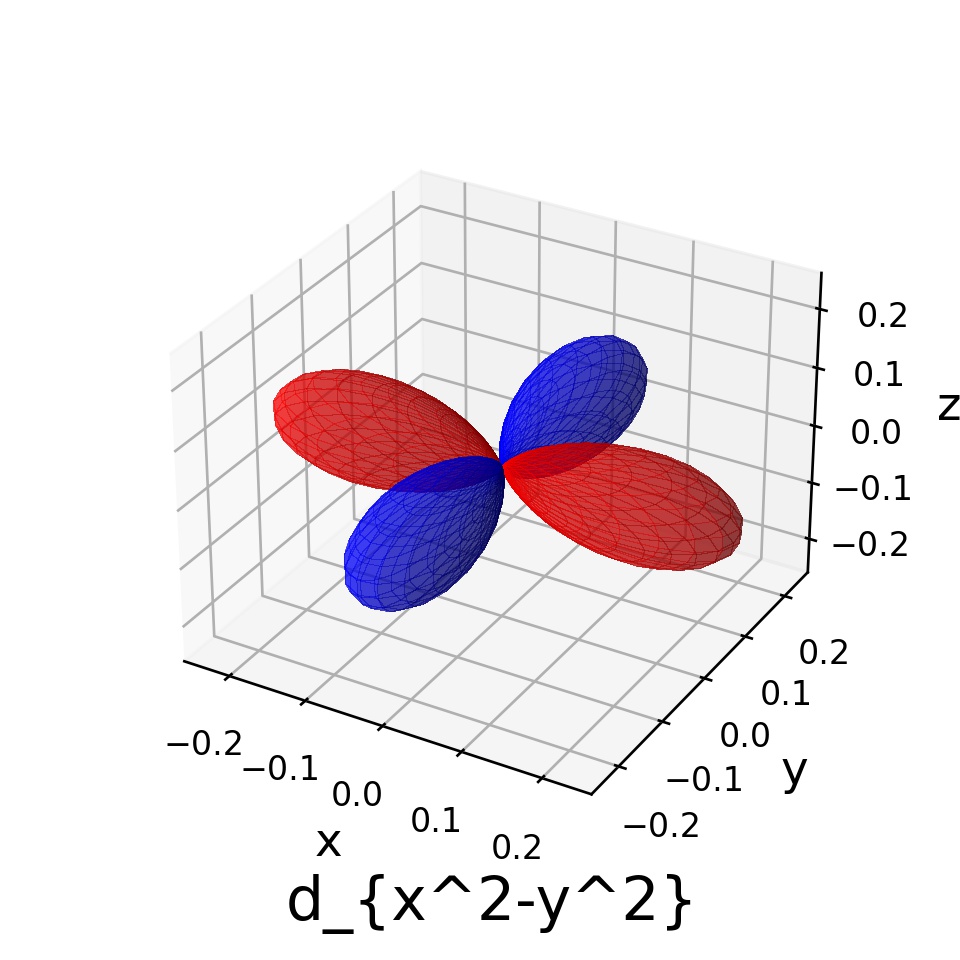
f:id:tsujimotter:20210627222447j:plain:w240

慣習にしたがって、上から順に $d_{xy}, \; d_{yz}, \; d_{z^2}, \; d_{zx}, \; d_{x^2 - y^2}$ と呼びます。

これらがd軌道の形ということですね！

5. Pythonのmatplotlibを使ったプログラム

最後に今回作ったプログラムを紹介しましょう。

まず、このプログラムはPython 3を想定して作っています。また、以下の２つのライブラリをインストールする必要があります：

numpy
matplotlib

以下が今回描画に使ったプログラムです。

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as axes3d

import math


# 球面調和関数（ただし、実関数表示したもの）
def spherical_harmonics(theta, phi, l, m):
    if l == 0:
        if m == 0:
            # l=0, m=0
            return np.sqrt(1.0/(4*np.pi))
    if l == 1:
        if m == 0:
            # l=1, m=0
            return np.sqrt(3.0/(4.0*np.pi)) * np.cos(theta)
        if m == 1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.cos(phi)
        if m == -1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.sin(phi)
    if l == 2:
        if m == 0:
            return np.sqrt(5.0/(16.0*np.pi)) * (3.0*(np.cos(theta)**2) - 1.0)
        if m == 1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.cos(phi)
        if m == -1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.sin(phi)
        if m == 2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.cos(2*phi)
        if m == -2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.sin(2*phi)


        
names = [["s"], ["p_y", "p_z", "p_x"], ["d_{xy}", "d_{yz}", "d_{z^2}", "d_{zx}", "d_{x^2-y^2}"]]

theta, phi = np.linspace(0, np.pi, 40), np.linspace(0, 2 * np.pi, 80)
THETA, PHI = np.meshgrid(theta, phi)

for l in range(3):
    for m in range(-l,l+1):
        fig = plt.figure(figsize=(4.0, 4.0))
        ax = fig.add_subplot(1,1,1, projection='3d')
        
        # 図のタイトルをイイ感じの場所に
        ax.set_title("{}".format( names[l][l+m] ), y=-0.15, size = 18)

        R = spherical_harmonics(THETA, PHI, l, m)**2
        X = R * np.sin(THETA) * np.cos(PHI)
        Y = R * np.sin(THETA) * np.sin(PHI)
        Z = R * np.cos(THETA)
        
        # 軸の設定
        ax.set_xlabel("x", size = 14)
        ax.set_ylabel("y", size = 14)
        ax.set_zlabel("z", size = 14)
        
        # x,y,zの表示範囲を設定
        ax.set_xlim3d(-0.25,0.25)
        ax.set_ylim3d(-0.25,0.25)
        ax.set_zlim3d(-0.25,0.25)
        
        # 色付けのルールを設定
        colortuple = ('r','b')
        COLORS = np.empty(THETA.shape, dtype=str)
        for y in range(PHI.shape[1]):
            for x in range(PHI.shape[0]):
                th = THETA[x,y]
                ph = PHI[x,y]
                if spherical_harmonics(th, ph, l, m) > 0:
                    # 球面調和関数の値が正であれば「赤」
                    COLORS[x, y] = colortuple[0]
                else:
                    # 球面調和関数の値が負であれば「青」
                    COLORS[x, y] = colortuple[1]
        
        # (l, m) に対応するグラフをプロット
        plot = ax.plot_surface(
            X, Y, Z,facecolors=COLORS, rstride=1, cstride=1,
            linewidth=0, antialiased=False, alpha=0.5)
        
        # ファイルを保存する
        plt.savefig("{}.jpg".format(names[l][l+m]),dpi=240)
        # グラフを表示
        plt.show()

上記のPythonコードを実行すると、同じディレクトリに画像が９枚生成されます。

このプログラムは

球面調和関数の定義（spherical_harmonics関数）
定義した関数を使ってグラフを描画する

という部分によって構成されています。

球面調和関数の定義の部分についてですが、今回は球面調和関数の手計算による計算結果を直接spherical_harmonics関数内に記述する形を取りました。

これだと一般の $l, m$ について計算できないわけですが、実際ルジャンドル陪多項式を計算するのは結構面倒なのでこのようにしています。

多項式の微分を計算しているだけなので、もう少しがんばればできそうな気もしますが、今回はやめておきます。

書いたあとで気づいたのですが、実はscipyというライブラリでは、球面調和関数 $Y_{l, m}(\theta, \phi)$ を直接計算してくれる関数があります。
docs.scipy.org

すごいですね！　便利な世の中になったものです。
（ちなみに、ルジャンドル陪多項式自体もscipyで計算できます！）

ただし、scipyで計算されるのは「複素関数」なので、今回やったように実関数に直してあげる必要があります。その点に注意してお使いください。

上記のコードは、グラフごとに画像を１枚ずつ生成するコードでしたが、以下はすべてをまとめて１枚の画像としてプロットするためのコードです。add_subplotをつかって、縦3×横5のグラフを生成するように変更しています。

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as axes3d

import math


# 球面調和関数（ただし、実関数表示したもの）
def spherical_harmonics(theta, phi, l, m):
    if l == 0:
        if m == 0:
            # l=0, m=0
            return np.sqrt(1.0/(4*np.pi))
    if l == 1:
        if m == 0:
            # l=1, m=0
            return np.sqrt(3.0/(4.0*np.pi)) * np.cos(theta)
        if m == 1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.cos(phi)
        if m == -1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.sin(phi)
    if l == 2:
        if m == 0:
            return np.sqrt(5.0/(16.0*np.pi)) * (3.0*(np.cos(theta)**2) - 1.0)
        if m == 1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.cos(phi)
        if m == -1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.sin(phi)
        if m == 2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.cos(2*phi)
        if m == -2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.sin(2*phi)


        
names = [["s"], ["p_y", "p_z", "p_x"], ["d_{xy}", "d_{yz}", "d_{z^2}", "d_{zx}", "d_{x^2-y^2}"]]

theta, phi = np.linspace(0, np.pi, 40), np.linspace(0, 2 * np.pi, 80)
THETA, PHI = np.meshgrid(theta, phi)

fig = plt.figure(figsize=(12.0, 9.0))
for l in range(3):
    
    for m in range(-l,l+1):
        # 3x5のサブプロット（左から順にm=-lからm=lまでプロットする）
        ax = fig.add_subplot(3,5,3+m+5*l, projection='3d')
        
        # 図のタイトルをイイ感じの場所に
        ax.set_title("{}".format( names[l][l+m] ), y=-0.35)

        R = spherical_harmonics(THETA, PHI, l, m)**2
        X = R * np.sin(THETA) * np.cos(PHI)
        Y = R * np.sin(THETA) * np.sin(PHI)
        Z = R * np.cos(THETA)
        
        # x,y,zの表示範囲を設定
        ax.set_xlim3d(-0.25,0.25)
        ax.set_ylim3d(-0.25,0.25)
        ax.set_zlim3d(-0.25,0.25)
        
        # 色付けのルールを設定
        colortuple = ('r','b')
        COLORS = np.empty(THETA.shape, dtype=str)
        for y in range(PHI.shape[1]):
            for x in range(PHI.shape[0]):
                th = THETA[x,y]
                ph = PHI[x,y]
                if spherical_harmonics(th, ph, l, m) > 0:
                    # 球面調和関数の値が正であれば「赤」
                    COLORS[x, y] = colortuple[0]
                else:
                    # 球面調和関数の値が負であれば「青」
                    COLORS[x, y] = colortuple[1]
        
        # (l, m) に対応するグラフをプロット
        plot = ax.plot_surface(
            X, Y, Z,facecolors=COLORS, rstride=1, cstride=1,
            linewidth=0, antialiased=False, alpha=0.5)
        
plt.savefig("Y.jpg",dpi=240)
plt.show()