tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

二項係数を求める関数の作り方 (Ruby編)

数学 ruby 技術系

「二項係数」って、数学系のプログラムを組んでいると割とよく登場するのですが、だいたいいつも計算方法が分からなくてググるのですよね。（私だけ？）

しかも、ググったところで、あまりよい方法は見つからなかったりするのです。
（よく出てくるのは、プログラミング初心者の書いた Yahoo! 知恵袋の質問記事だったり。）

探すための時間がもったいないなと思いましたので、自分の備忘録的に書いておきたいと思います。

短い記事になるかな、と思ったら案外検討すべきことがいろいろ出てきて、ちょいとボリューミーな記事になりました。

ちなみに，スクリプトはすべて Ruby で書いています。理由は，単に tsujimotter が Ruby が好きだからです。笑
たぶんほかの言語に変換することは簡単だと思いますので，アルゴリズムだけ確認してお好きな言語で実装してみてくださいね。

二項係数の定義

n 個のものから， k 個のものを選ぶ組み合わせの総数を，

\displaystyle \binom nk

と書いて，これを二項係数と呼びます。

なぜ二項「係数」なのか，というと「二項展開」というのがあって，二項係数を使って

\displaystyle (x+1)^n = \sum_{k=0}^{n} \binom nk x^k

のようにかけるのでしたね。二項展開の係数だから「二項係数」なのです。

余談ですが、この二項係数は tex だと "\binom nk" と書けばよいのですよ。便利ですね。わたくし、今日はじめて知りました。笑

そういえば、高校のときは {}_nC_k とも書きましたね。今回は，tex で書きやすいということもあり， \displaystyle \binom nk でいきたいと思います。

シンプルなソリューション（再帰）

さて、この二項係数ですが、以下のような式で書くことができますね。

\displaystyle \binom nk = \binom {n-1}{k-1} + \binom {n-1}{k}

え、そんな式見覚えないって？冗談言わないで下さい。笑

高校のときにやりませんでした？
n-1 個のボールと 1 個のボールに分けて， 1 個のほうが選ばれる場合と選ばれない場合で，場合分けするやつですよ。

・・・

さて、この式は， \binom nk という式を，より小さい n-1 や k-1 を使った式に置き換えている，と見ることができます。
したがって，「再帰」を適用しやすい式の形をしているわけです。

この式をそのまんま，Ruby を使って書いたものが，次のスクリプトです。

# 二項係数 ver. 1
#   再帰をつかってシンプルに計算するバージョン
def binom_v1 n,k
   if k==0 then 
      return 1
   elsif n==k then
      return 1
   else
      return binom_v1(n-1,k-1)+binom_v1(n-1,k)
   end
end

あ，言い忘れましたが， n, k を n-1, k-1 に落としていくと，いつまでたっても終わりませんから、 n=1 や n=k のときに止めてあげる必要がありますね。上の２つの条件はそれらを表現しています。


さて，この方法さえあれば，とりあえずはなんとかなるでしょう。

これで満足できる方は，以下の説明を読む必要はまったくありません！


・・・


さて。

人間とは欲張りなもので，やっていくうちにいろいろと不満が出てくるものです。


上の実装における一番の問題点は，計算が遅いということです。


ためしに，次のようなスクリプトで実行速度を測ってみましょう。 \binom nk を， n=0 からはじめて n=29 まで実行しています。ただし， k の値は， n/2 の整数部分をとっています。

require 'benchmark'

# (中略) binom_v1 の定義をここに書く

# 二項係数 nCk を計算する関数
def binom n,k
   binom_v1 n,k
end

### ベンチマークテスト
##### ログデータは "benchmark.csv" に格納
def binom_test_1
   File.open("benchmark.csv", "w") do |io|
      30.times do |i|
         n = i
         k = i/2
         b = 0
         result = Benchmark.realtime do
            b = binom n,k
         end
         io.puts "#{n},#{k},#{b},#{result}"
      end
   end
end

# テスト実行
binom_test_1


実行してみるとわかりますが，かなり時間がかかります。。。
私の環境では，一分以上かかりました。

横軸に n を，縦軸に実行時間（単位：秒）をとったグラフが次の図です。

f:id:tsujimotter:20150207045905p:plain:w400

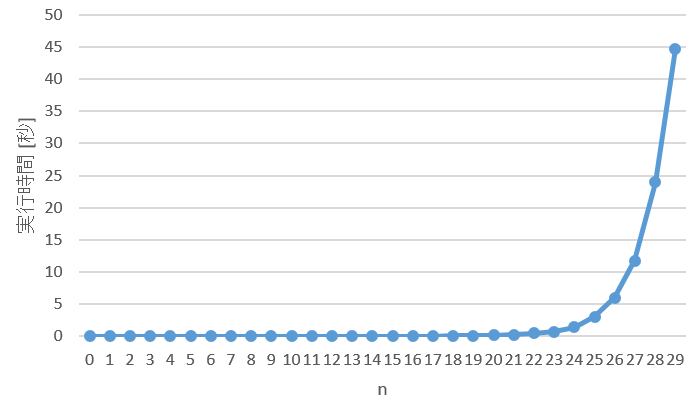
n=29 ではたしかに 40 秒以上もかかっていますね。しかも性質が悪いことに，指数関数的に増加していることが分かります。


これは当然といえば当然で，再帰で実行されるときに，２つに分岐しているからなのです。分岐した先でもさらに２分岐して，その先でも２分岐して・・・と，倍々ゲームで増えていきます。結局，実行時間は 2^n に比例するというわけです。

まぁ， n = 20 程度で，しかもそれほど繰り返し利用しない，という条件であればこの実装でも何ら問題ないでしょう。逆に n = 100 まで計算したい，となるとこの方法では絶望的ですね。おまけに，再帰があまりに続くとStackOverflowの可能性もあります。

この辺は，求める要求次第です。絶対的な方法などないのです。

私は「とある目的」により， n=100 くらいまで計算したかったので次の方法に進みます。

計算量を劇的に減らす方法

先ほどの再帰において，最大の問題は「分岐が発生すること」でした．分岐によって倍々ゲームで実行時間が加算されていくことが問題だったのわけです。

ここで，先ほどの再帰において分岐をなくしてしまえば，指数関数的な実行時間の増加はなくなり，実行時間は n に対して線形になります。

そんなことができるんでしょうか。

実はできるんです。この式を使いましょう。

\displaystyle \binom nk = \binom {n-1}{k-1} \frac{n}{k}

たしかに，これなら２通りの二項係数に分岐することはありません。しかし，こんな式，本当に成り立つんでしょうか。

この疑問には，結構簡単に答えることができますのでやってみましょう。


そもそも高校では，二項係数はこのように習いましたよね。

\displaystyle \binom nk = \frac{n!}{k!(n-k)!}

この n, k を，それぞれ n-1, k-1 に落としてあげると，こうなります。

\displaystyle \binom {n-1}{k-1} = \frac{(n-1)!}{(k-1)!(n-k)!}

下の式で上の式を割ってあげると，目的の式が得られますね。


さぁ，というわけで，Rubyのスクリプトに直していきましょう。

# 二項係数 ver. 2
#   より高速に計算するバージョン
def binom_v2 n,k
   k = [k, n-k].min

   if k==0
      val = 1
   else
      val = binom_v2(n-1,k-1)*n/k
   end

   return val
end


さて，最初の行に変なことをやっていますね。 k と n-k のいずれか小さいほうを k に再代入しているわけなのですが，いったい何をやっているのでしょうか。

これはですね，より計算量を減らすための対策なのです。

二項係数には，以下のような性質がありました．

\displaystyle \binom nk = \binom {n}{n-k}

これを使って，次に計算する再帰の回数をより小さくしたかったというわけです。まぁ小手先のテクニックですね。

みなさんもやりませんでした？
\binom {6}{4} を計算するより \binom {6}{2} を計算したほうが早そうだなあ、みたいな。
これと同じことです。


さて、一応最初のバージョンと値が一致するかどうかは、以下のようなスクリプトで確認できます。

# （いろいろ省略）

### v1, v2 のどちらのバージョンも同じ値を返すことの確認
def binom_test_2
   20.times do |n|
      n.times do |k|

         b1 = binom_v1(n,k)
         b2 = binom_v2(n,k)

         if b1!=b2 then
            puts "#{b1},#{b2}"
         end
      end
   end
end

### 実行テスト
#binom_main_1
binom_main_2


最初のときと同じく，実行時間を測ってみると，びっくりするぐらい改善されています。

require 'benchmark'

# (中略) binom_v1, binom_v2 の定義をここに書く

# 二項係数 nCk を計算する関数
def binom n,k
   #binom_v1 n,k
   binom_v2 n,k
end

### ベンチマークテスト
##### ログデータは "benchmark.csv" に格納
def binom_test_1
# （中略）
end

# テスト実行
binom_test_1
#binom_test_2


実行してみると，なんとほとんど 0 秒です。笑
笑っちゃうぐらいはやいですね。

40 秒って何だったのでしょう。。。

このベンチマークのライブラリは，「ミリ秒」単位で測れるのですが，一回の実行でミリ秒もかからないのですね。


というわけで，実用上はずいぶん改善したので，もういいかなと思うかもしれませんが，実はもう少し改善できます。
実際問題，一回の実行程度では，ほぼ計算の時間がかからなかったわけですが， n をある程度大きくして繰り返し実行すると，多少時間がかかるわけです。

そこで次の項では，繰り返し実行する際に効果的な方法を紹介します。

キャッシュを使う方法

この方法は，まぁよくある高速化の方法なのですが，一度計算した値を保管しておけばよいのです。一時的に保存しておく値のことを「キャッシュ」といいますね。

幸い，今回の関数は整数を引数にとるわけなので，キャッシュはやりやすいわけです。

大したことはないので，さっそく実装してみましょう。

_MAXNUM=1000
$array = Array.new(_MAXNUM+1).map{Array.new(_MAXNUM+1, 0)}

# 二項係数 ver.3
#    既に計算した値は, 二次元配列 $array にキャッシュされて次回呼び出し時に使用される 
def binom_v3(n,k)
   if $array[n][k] == 0 then
      k = [k, n-k].min

      if k==0 then
         val = 1
      else
         val = binom_v3(n-1,k-1)*n/k
      end

      $array[n][k] = val
      return val

   else
      return $array[n][k]
   end
end


今回は，_MAXNUM という変数を用いて，1000x1000 の配列を事前に用意しています。関数で使用するためには，グローバル変数にしなければいけないので，array の前に $ マークがついていることに注意です。

ちなみに， n や k に 1000 以上の値を入れると，エラーが発生しますので注意してください。この辺りは，もっとスマートに実装できるような気もしますが，いい方法を考えるのは面倒なのでやめておきます。


ともかく，この方法を使えば，一回使用した n, k の組み合わせに対しては，配列から取り出すだけなので，一瞬で計算が返ってきます。

私の「とある目的」では，二項係数の同じ組み合わせを大量に計算するようなものだったので，この効率化は必須なのでした。

まとめ

いかがだったでしょうか。

今回は，二項係数の再帰的な計算の実装方法を，

  1. シンプルに二分岐
  2. 線形化
  3. キャッシュ化

の３パターンで紹介しました。

どれを使うかは，そのときの条件次第ですね。

n が十分小さくて，手早く使いたいだけなら 1. でも構いませんし， n が 30 を超えるなら 2. を使えばいいですし，さらに繰り返し同じ値を使うなら 3. というわけですね。ただし，キャッシュのメモリの上限には十分注意してくださいね。


今回のすべてのスクリプトをまとめたコードは，以下のサイトに上げておきましたので，よかったらお使いください。

binom.rb - 二項係数を３パターンで実行するスクリプト


さて，今回 tsujimotter の「とある目的」のために書いた記事なのですが，いったい何の目的で使うのでしょうか。

そのうちこのブログでも紹介するかもしれませんが，今はもったいぶって内緒にしておきます。笑

それでは，今日もガッツリ書いてしまいましたが，この辺で失礼します。


追記：続きです！
tsujimotter.hatenablog.com