前回のtsujimotterのノートブックでは ベータ関数 が登場しましたが、ベータ関数にはもう少し親しみやすい導入があります。それが高校数学でいわゆる 1/6公式 と呼ばれる積分の公式です。
このブログでも何度か登場した 超幾何関数 も関係します!お楽しみに!

なお、今回の記事の内容は、すどさんと黒木玄さんの一連のツイートに影響を受けて書いたものです。ツイートのリンクは記事の最後にまとめて紹介しております。
本記事の内容は、お二方の元ツイートだけを読んでも十分理解できるものとなっております。しかしながら、自分で計算してみて面白くなり、やはり自分の言葉でもまとめてみたいと思うようになりました*1。とても楽しい話題を提供してくださったすどさん、黒木玄さんに感謝しつつ、執筆させていただきます。
tsujimotterのノートブックで「ベータ関数」の話題が登場したばかりですので、タイミング的にもちょうどよいかと思っています。ぜひ最後まで読んでいただければと思います。
「1/6公式」とは?
直線 と2次関数
によって囲まれる面積
について考えてみましょう。

図のように と
は2点で交わるとし、交点それぞれの
座標を
とします(
と仮定します)。
このとき、面積 が
と表せるというのが、いわゆる 「1/6公式」 です。
この公式を初めて教えてもらったときは、面積の式に「交点の 座標
」と「2次関数の係数
」しか現れないことに驚きました。その他の情報をまったく必要としないのですね。ちょっと不思議な感じがします。
「1/6公式」の背景には次のような理屈があります。
まず、面積 を「符号も含めて」考えることにすると、
と
軸で囲まれた図形

の面積から、 と
軸で囲まれた図形

の面積を引いたものとして表せます。
もし ならば、
から
の範囲で、2次関数は直線の上にきます。この場合は面積
が「負」になるように符号を設定しています。
つまり
ということですね。積分の差は、被積分関数同士の差をとって積分したものと一致しますので
となります。
なので、
は2次関数となります。
一般の2次関数を決定するためには、「2次の係数」と「2つの根」を決定すれば十分です。 の2次の係数は
ですね。また、2つの根は
です。したがって
となります。
これを から
の範囲で積分すれば、面積
が得られますね。すなわち
ということです。
あとは右辺の積分を計算すればよいというわけですね。
あとでもっとスマートな方法を紹介しますが、愚直に考えても公式は得られます。つまり被積分関数を
のように展開し、それらを項別に積分します。
以上の計算により、面積 が
と表せることが示されました。なお、係数 に絶対値をつければ、面積の符号を常に正にとることができます。
しかしながら、積分計算が難解すぎて間違いそうですし、できることならやりたくないですよね。「一度くらいやってみようか」程度であればよいかもしれませんが。
もう少しスマートに式変形することを考えましょう。
置換積分によってスマートに
変数を置き換えることで積分を簡単化することを目指します。
今、 から
の範囲で積分しています。ここで、積分範囲が
から
になるように、変数
を「圧縮」した新しい変数
を用意することにしましょう。こんなイメージです:
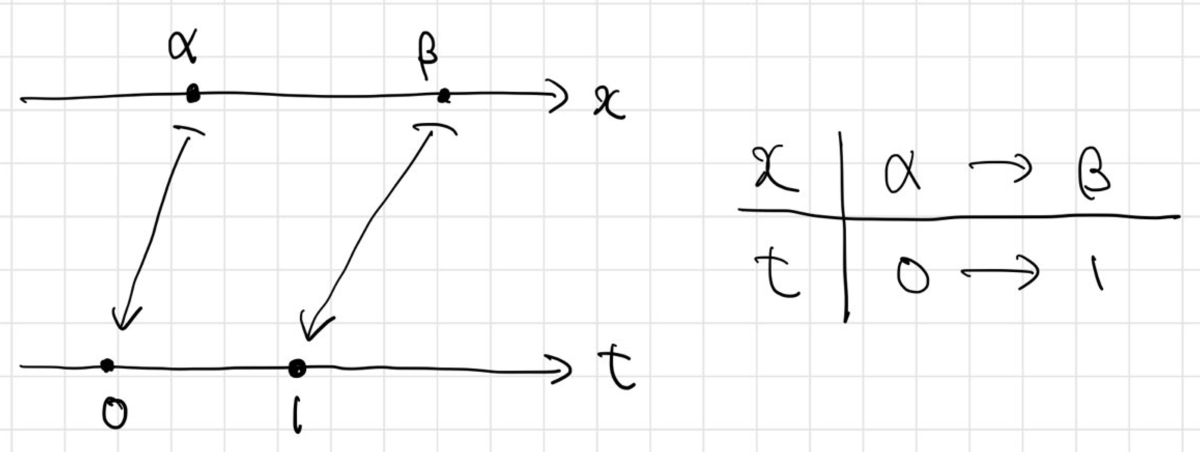
このような変数変換は、いくらか試行錯誤してみることで得られます。積分範囲の開始点を から
にずらしたいので、
を
とします。すると、図のようになりますね:


以上の議論により、新しい変数 を
とすればよいことが分かりました。
逆に、 を
を用いて表すことができます:
これを使うと、次の変換則が得られます:
これらの変換則を用いて置換積分を実行すると、次のようになります:
3つの変換則によって、それぞれ が1つずつ出てくるので、
が現れるわけですね。
あとは、 に関する積分
を計算できればよいわけですが、単に展開して項別積分することで計算できます:
前節と比べて、ずいぶん簡単な計算になりましたね!
ベータ関数・ガンマ関数に帰着させる
最後に計算した積分 について、もう一つの見方を提示しましょう。
もう察しがついている人はいるかと思いますが、上記の積分は ベータ関数 の特殊値になっています。ベータ関数の定義は、次のものでした:
は収束する。 をベータ関数という。
ここで とした
が上記の積分というわけですね。
つまり、面積 は
として、ベータ関数の特殊値によって表せるということですね! 面白いです!
このベータ関数の特殊値が になることについては、ガンマ関数 を使うことで、より深く理解できます。ガンマ関数
は、次のように定義される関数です。
は収束する。 をガンマ関数という。
ガンマ関数の積分に対して、部分積分を適用することで
が得られます。加えて であることから、ガンマ関数は階乗関数の一般化だと思うことができます。
実際、1以上の整数 に対して
が成り立ちます。
ガンマ関数とベータ関数の間には、以下のような有名な公式があります:
この定理が最後のキーとなります。

- 作者:杉浦 光夫
- 発売日: 1980/03/31
- メディア: 単行本
この定理とガンマ関数が階乗関数である事実を使うと
という感じに、 が得られます。
つまり「1/6公式」の分母の「6」は
から来ていたことが分かりました! 面白いですね!!
このようにして考えると、積分の公式をもっと一般化できそうだということに気づきます。
実際、一般の に対して、全く同様の式変形によって次の式が得られます:
特に が1以上の整数であるとき、上記の積分は次のように表せる:
さらなる高みへ:超幾何関数との関係
前節までは、実軸上の2点 (
)において、それぞれ重複度
の零点を持つような
次多項式の積分を考えてきました。明示的には説明していませんでしたが、そのような積分を計算してきたと言えます。

これを実軸上の3点 (
)に拡張した問題を考えてみましょう。
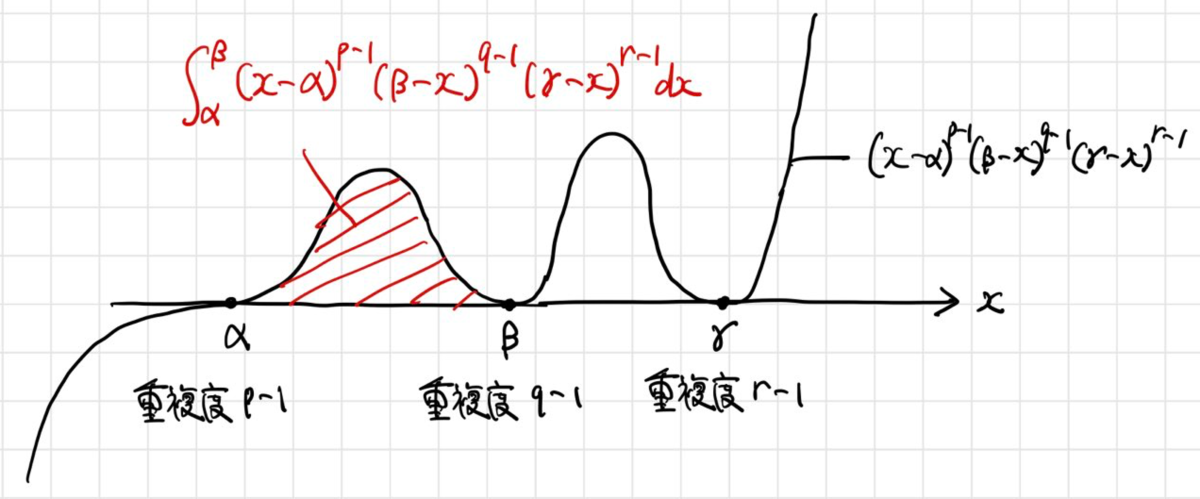
すなわち、この節を通して考えたい積分の問題はこちらです。
この積分が 超幾何関数の積分表示 を使って表せることを示しましょう。(「超幾何関数の積分表示」については、議論の中で触れたいと思います。)
問題の積分に対して、前節までと同じように
という変数変換を行います。 から
までの積分範囲は、
から
までに変わります。
また、
という変換則は前節とまったく同じです。
次に、 についてですが、
とすることができます。先の変換則とは異なり、 が飛び出てくるのがポイントです。
これらの変換則を用いて、問題の積分を次のように変形できます:
さて、最後の積分を考えるために、「超幾何級数の積分表示」を思い出しましょう:
定理(ベータ関数とガンマ関数の関係)より
なので、逆に超幾何積分がベータ関数と を用いて
と表せると思ってもいいですね。
ここで問題の積分は、 とすることで超幾何関数の積分表示に一致します。よって、次のように計算できます:
ただし、超幾何関数の積分表示の条件を考慮して
かつ
または
が非負整数
を満たす必要があります。
前者の条件は を 1 以上の整数としているので、そのままで成立します。後者の条件も
を 1 以上の整数としているので、そのまま成立します。もちろん、
を満たしていれば、
は任意にとっても問題ありません。
というわけでこの節の問題に対する解答をまとめると、こうなります:
が成り立つ。
これまでベータ関数や超幾何関数を遠い存在だと思っていた人もいるかと思います。しかしながら「1/6公式」という高校数学的な問題から自然な一般化を考えると、なんとベータ関数や超幾何関数が現れるというのです! 面白いですね!
今回の話を通して、ベータ関数や超幾何関数が身近に感じられてきたのではないでしょうか?
それでは今日はこの辺で!
参考にさせていただいたツイートたち
冒頭で述べた通り、今回の内容はすどさんと黒木玄さんの以下のツイート(およびその関連ツイート)に影響されて書いたものです。とても楽しい話をTwitterで共有してくださり、ありがとうございます。あらためて感謝申し上げます。
すどさんのツイート:
一般にいう「数学の先生を困らせる系証明」(結城さんごめんなさい)。でもこっちが本質だと個人的には思っていたりする。@hyuki pic.twitter.com/cwgoKCNTf4
— すど (@ysmemoirs) 2015年11月22日
あと,暗記系の代表格「 6 分の 1 公式」をこうしちゃうとか……https://t.co/d4GsqRce7w
— すど (@ysmemoirs) 2019年1月29日
黒木玄さんのツイート:
積分が
— 黒木玄 Gen Kuroki (@genkuroki) 2019年1月29日
-(β-α)^m×(定数)
になることが明らかになるまで変形すれば、定数部分がものすごく役に立っているベータ函数になっていることがあらわに見えます。
「定期試験数学」「受験数学」っぽいノリではなく、「役に立っている数学」まで視界を広げることは、数学教育全般で大事だと思います。< pic.twitter.com/TqlrT7yhBU
さらにおまけ。
— 黒木玄 Gen Kuroki (@genkuroki) 2019年1月30日
例えばα<β<γとし、ちょうどx=α,β,γでそれぞれA,B,Cの重複度の零点を持つ場合を考えると、(Gaussの)超幾何函数が出て来ます。
この意味で高校の数学の授業時間中に「超幾何函数まで一般化して調べること」を提案する高校生がいても不思議でも何でもありません! pic.twitter.com/mnMqX2AcoU
#数楽 微小追記版
— 黒木玄 Gen Kuroki (@genkuroki) 2019年2月7日
超幾何函数は高校数学に自然に出て来る。
∫_α^β (x-α)^{p-1} (β-x)^{q-1} (γ-x)^{-b} dx
= (β-α)^{p+q-1} (γ-α)^{-b}
×∫_0^1 t^{p-1} (1-t)^{q-1} (1-zt)^{-b} dt
= (β-α)^{p+q-1} (γ-α)^{-b}
×B(p,q) Σ_{k=0}^∞ ((p)_k (b)_k)/((p+q)_k k!) z^k
ここで z = (β-α)/(γ-α). pic.twitter.com/iAnFivfozr
また、清史弘さんがタイミングのよいツイートをなさっていましたので紹介させていただきます。
【問題】
— 清 史弘 (@f_sei) 2020年9月27日
次の問題は大学生以上になると、特に難しくはないと思いますが、高校生、受験生の皆さんはどうすればよいか、アイディアはありますか? #清史弘の問題 pic.twitter.com/KLrlN3nd3L