素数大富豪 Advent Calendar 2018 の24日目の記事です。
本記事は、素数大富豪 Advent Calender 2018 の24日目の記事として、素数大富豪プレーヤーのレーティングを算出する手法について、筆者による提案手法を紹介したいと思います。また、その手法を用いて過去の大会における結果を元にレーティングを算出しましたので、その結果も合わせて紹介したいと思います。
お詫びと謝辞
今回の記事は、昨年に企画された素数大富豪 Advent Calender 2018の24日目に書かれるはずだった記事です。
以下の画像をご覧いただいてわかるように、素数大富豪 Advent Calender 2018では、私だけ記事を書いておりません。
私のせいで25日分が揃わず、大変申し訳ございません。。。
1年越しになりましたが、389日目にしてようやく記事を書くことができましたので、投稿させていただきます。
また、今回の分析に用いたデータであるMATH POWER2017の勝敗データについては、二世さんに作成いただきました。また、せきゅーん杯の勝敗データについては、はなぶさんにご提供いただきました。お二人に心から感謝いたします。
はじめに
2014年にトランプゲーム「素数大富豪」が発案されてから5年経ちました*2。近年では、プレー人口も一定の規模になり、大会等 *3*4*5 も不定期で開催されるようになりました。
一方で、プレーヤー間のレベル差が大きくなってきたという現状も報告され、それに伴い初心者のプレーヤーの参入のハードルが高くなってきたのではないかという問題も指摘されています [要出典]。
初心者のプレーヤーがいきなり強いプレーヤーと対戦することにより、モチベーションを下げてしまう「不幸な接触」を防ぐために、筆者は素数大富豪のレーティング方法を提案しました。
本記事では、筆者の提案した「イロレーティングに基づく素数大富豪のレーティング方式*6*7」を紹介するとともに、そのレーティングに基づいて行った素数大富豪大会のレーティング結果について紹介し、その結果を議論したいと思います。
なお、筆者の過去の研究 [6] ではMATH POWER杯2016の対戦結果を元にしたレーティングを、[7] では以降4大会の結果を加えたレーティングを計算しています。本記事はそれぞれの結果をまとめた内容となっています。
イロレーティング *8
イロレーティングとは、2人対戦ゲームにおける実力を測定する算出方法であり、チェスの公式戦において実際にレーティングに用いられています。本研究では、素数大富豪の対戦においてイロレーティングを用いることを提案します。
イロレーティングは、次の2つの前提を元に算出されます。
- 200点のレート差があるプレーヤー間では、レートの高い側が約76パーセントの確率で勝利する
- 平均的なプレーヤーのレートを1500とする
プレーヤー のレートをそれぞれ
としたとき、
が
に勝利する確率
は式
で算出されます。
まず、 が試合を行った際のゲーム数を
とし
の勝ち数を
とします。
なお、今回の結果の中に、引き分けとなった試合は含まれませんでした。
このとき、 のレートは次のように更新されます。
ここで、 は定数です。 本研究では、チェスの大会等で一般に用いられる
を用います。
式 の計算を繰り返すことでレートが次々に更新され、最終的に妥当な勝利確率になるところでレートが収束します。実際のレート計算のアルゴリズムは次の通りです。

実験結果
MATH POWER杯2016・2017・2018の3大会のほか、2018年1月に開催された「せきゅーん杯」、2019年10月に開催された「マスパーティ杯」を対象とします。試合総数は105、ゲーム総数は264、プレーヤー総数は70です。
各大会の試合データと該当大会までの通算のレーティングを結果として示します。
MATH POWER杯2016(2016年10月4日・5日開催)
- 参加者数:16名
- データに使用された(放送された)参加者数:12名
- ゲーム数:10試合25ゲーム(放送された分のみ)
- 1対1トーナメント形式
- 2ゲーム先取(決勝のみ3ゲーム先取)
結果は表1の通りです。
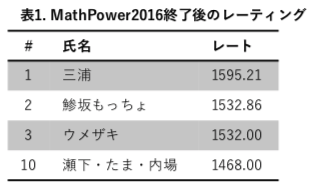
MATH POWER杯2017(2017年10月7日・8日開催)
- 参加者数:27名(内新規22名)
- データに使用された(放送された)参加者数:13名(累計20名)
- ゲーム数:11試合27ゲーム(放送された分のみ)
- 1対1トーナメント形式
- 2ゲーム先取(決勝のみ3ゲーム先取)
累積のレーティング結果(一部抜粋)は表2の通りです。
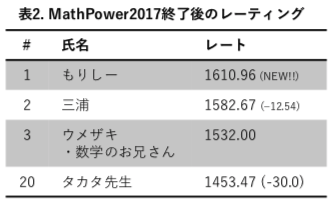
せきゅーん杯(2018年1月14日開催)
- 参加者数:16名(内新規10名)
- データに使用された(放送された)参加者数:16名(累計31名)
- ゲーム数:34試合78ゲーム
- 予選:4名1グループ総当たり(2ゲーム先取)
- 決勝:1対1トーナメント(2ゲーム先取)
累積のレーティング結果(一部抜粋)は表3の通りです。

MATH POWER杯2018(2018年10月6日・7日開催)
- 参加者数:24名(内新規11名)
- データに使用された参加者数:24名(累計43名)
- ゲーム数:23試合67ゲーム(全試合のデータ使用)
- 1対1トーナメント形式
- 2ゲーム先取(決勝のみ3ゲーム先取)
累積のレーティング結果(一部抜粋)は表4の通りです。
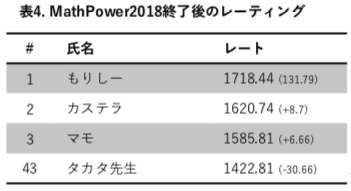
マスパーティ杯(2019年10月19日・20日開催)
- 参加者数:28名(内新規13名)
- データに使用された参加者数:28名(累計56名)
- ゲーム数:27試合67ゲーム(全試合のデータ使用)
- 1対1トーナメント形式
- 2ゲーム先取(決勝・準決勝のみ3ゲーム先取)
累積のレーティング結果(一部抜粋)は表5の通りです。

5大会終了後のレーティング結果

画質が悪くてすみません。
表6にはレーティング1500のプレーヤーが14名入っています。これらのプレーヤーは大会に登録されたものの、(放送されなかったという理由により)ゲーム数・勝利数のデータが得られなかったプレーターです。レートが一度も更新されず、初期値である1500のままとなっています。
図1では、代表的なプレーヤー(最終的なレーティングにおける上位7名)についてのレーティングの推移をまとめています。
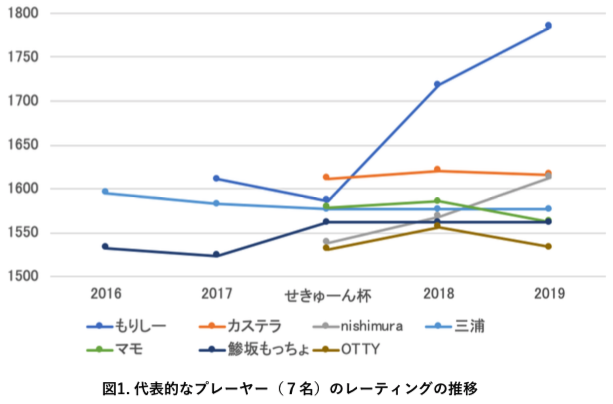
MATH POWER杯2016で優勝した三浦氏は、前半ではレーティング上位を保っていましたが、後半の大会には出場しなかったためレーティングが停滞しています。
最終的なレーティング最上位者のもりしー氏は、MATH POWER杯2016で優勝しレーティング最上位になり、その後せきゅーん杯で順位を落としましたが、以降は順当にレートを伸ばしていく推移を見せました。グラフからは、まだレーティングを上昇させそうな様子が観察されます。
考察
試合数・ゲーム数について
せきゅーん杯以降の大会について、試合数やゲーム数が大幅に増加しています。素数大富豪研究会2018における筆者の発表以降に開催された大会については、(放送するしないに関わらず)すべての試合でデータを記録するよう依頼しており、その結果データ数が大幅に増加する結果となりました。
したがって、後半3大会においては、大会に登録したすべてのプレーヤーのレートが計算されることになります。レーティング計算において、これらのデータ数が十分であったかについての考察は次の項で述べたいと思います。
レーティングの収束性
以下ではレーティングの収束性についての議論をします。一つの観点として、得られたレーティングの値 を用いて、式
を計算し、期待される勝率
を評価する方法が考えられます。
例として、MATH POWER杯2016の結果における最上位と最下位のプレーヤーのレートを考えます。最上位のプレーヤー(三浦氏)のレートは であり、最下位のプレーヤー(瀬下氏・たま氏・内場氏)のレートは
でした。これらを元に、最下位のプレーヤーが最上位のプレーヤーに勝利する確率
は、次のように計算されます。
すなわち、最下位のプレーヤーは最上位に32.5%の確率で勝利することになります。しかしながら、優勝プレーヤーに約3回に1回は勝利するという仮定は、やや現実的でないように考えられます。このような結果は、レーティングにおいてデータ数が少なかったことが要因と考えられます(MATH POWER杯2016の時点でのゲーム数は25)。
一方、マスパーティ杯までの5大会の結果における最上位のプレーヤー(もりしー氏 )と最下位のプレーヤー(辻順平氏(筆者)
)のレートを考えます。
に対する
の勝率は次のように計算されます。
すなわち、最下位のプレーヤーは最上位に10.8%の確率で勝利することになります。この結果は、優勝プレーヤーに対し最下位プレーヤーが約10回に1回は勝利するということを意味しますが、これは経験的にも十分妥当な結果かと思われます。
もちろん、このような評価は筆者による主観的なものであり、収束性を測るには十分とは言えません。
より客観的な分析のためには、ランダムで生成された試合結果のシミュレーションに基づいて、レーティングを計算した際の評価値と比較する方法が考えられます。この方法により、レート更新時のパラメータ の妥当性についても合わせて検証できると考えられます。これらについては今後の課題とします。
レーティングのインフレ
また、図1の結果からもわかるように、もりしー氏のレーティングが上昇し続けている傾向が見られます。
実際、イロレーティングに基づくレーティング法は、プレーヤーのレーティングが過大になるインフレ(あるいはその逆のデフレ)が生じる場合があることが知られている。今回の結果も、十分な試合数がなされていないため断定はできないが、このままインフレが続く可能性は考えられます。
試合数が少ないのにレーティングが高いプレーヤー
表6の結果を見ると、レートが1500以上のプレーヤーの中に、ゲーム数の合計が5未満のプレーヤーが5名います。これらのプレーヤーは、試合数は少ない中でたまたま勝率が高くなったプレーヤーであり、これらがより勝利数の多いプレーヤー(たとえば、40位のキグロ氏)よりもレートが高い結果となっており、妥当ではないという見方もできます。
素数大富豪研究会で教えていただいたのですが、ルービックキューブの公式大会のレーティング方法は、試合数の多いプレーヤーの方が相対的にレートが高くなるように設計されているそうです。今後の課題として、そのような方式との比較ができるかと思います。
プレーヤーの重複登録
素数大富豪研究会中に判明したことですが、最終的なレーティング結果において、同一人物が異なるプレーヤーとして登録されているケースが見受けられます。具体的には、以下の2名です。
- しろくま氏(24位と41位)
- ジャッカル氏(25位と38位)
また、14位のはなぶさん氏と55位のHF氏は同一人物です。これは大会ごとの登録名が異なるものになっていたために起きたケースです。たまたま知り合いだったために同一人物であることが判明しましたが、異なる登録名のプレーヤーに対し、その同一性を判別するのは困難な課題です。このような課題が上がったこと自体は、今回の研究の一つの成果かと思います。
レーティングを正しく計算するにあたっては、この同一性の問題は避けて通れない課題です。対策としては、登録者にIDを発行するレーティング協会等を作ることが考えられますが、容易なものではありません。
応用:レーティングの大会への利用
上記のような課題を抱える本研究のレーティング方式ですが、課題が解決すれば十分な応用が考えらえます。
一つは、大会運営に利用することです。レーティングが大きく異なるプレーヤーについては、ハンディキャップをつけるという方法が考えられます。イロレーティングの一つの特徴として、レート差から期待勝率が計算できるというものがあります。実際、5大会の結果における最上位と最下位のプレーヤーのレートさに基づいて、期待勝率が10.8%と算出されました。これらの勝率を元に、たとえば最上位プレーヤーが10ゲーム先取するか、最下位プレーヤーが1ゲーム先取したら勝敗が決定するように設計することも可能です。
実際、札幌で開催予定の素数大富豪大会札幌杯*9においては、レベルに応じた出場制限のついた部門が用意されていますが、そのような場合にレーティングを参照するという方法も想定されます。
おわりに
本研究では、素数大富豪で利用可能なレーティングを目的として、イロレーティングを用いた方式を提案しました。また、過去5大会の勝敗結果に基づいて、レーティングを実際に計算し、その妥当性を検証しました。
データ量が十分性やレーティングの収束性についてはまだ疑問があり、より詳細な分析が望まれるものの、十分な応用可能性が示される結果となりました。
Appendix: 使用したデータ
データは以下のDropboxリンクで共有しています。今後の研究にご活用ください。
(ただし、上記に問題としてあげた「データの重複」は解決していません。)
www.dropbox.com
参考文献
*3:[3] MATH POWER
*4:[4] 素数大富豪大会 せきゅーん杯 - connpass
*5:[5] マスパーティ 開催決定!
*6:[6] 辻順平,素数大富豪のレーティングに関する提案,素数大富豪研究会2018 (2018).
*7:[7] 辻順平,素数大富豪のレーティングに関する追調査,素数大富豪研究会2019 (2019).