「数体の素元星座定理」に関するプレプリントについて

2021年に入ってすぐに、とんでもないニュースが飛び込んできました。もちろん、数学のニュースです。

東北大学の研究チームによる論文のプレプリントがarXivで公開されました。タイトルは "Constellations in prime elements of number fields" で、こちらのリンクからアクセスできます：

Constellations in prime elements of number fields
Wataru Kai, Masato Mimura, Akihiro Munemasa, Shin-ichiro Seki, Kiyoto Yoshino
https://arxiv.org/abs/2012.15669

Wataru Kai, Masato Mimura, Akihiro Munemasa, Shin-ichiro Seki, Kiyoto Yoshinoの5名により発表されたプレプリントです。著者の一人であるShin-ichiro Seki（関真一朗）さんの名前は、今回の記事で何度か登場します。

上記の原稿はプレプリントですので、査読がなされたわけではありません。したがって、証明されたかどうかを確認するためには、自分で証明を読み込んで確認するほかありません。

普段、このようなプレプリントはなるべく紹介しないようにしているのですが、今回ばかりはどうしてもブログでご紹介したくなりました。というのも、証明されたとされる結果があまりにすごいからです！

英語で書かれた論文ですが、主定理の名称を日本語でいうなら

「数体の素元星座定理」

ということになります。いかにも興味をそそられる内容ですよね！

この「数体の素元星座定理」なる日本語訳については、関真一朗さんご自身のツイートから拝借させていただきました。

これに対し、我々はTerence Taoの予想を全ての数体に対して精密な形で解決しました。名付けて「数体の素元星座定理」
— せきゅーん (@integers_blog) 2021年1月1日

今回の記事では、上記のプレプリントについて

「星座」とはいったいどういう概念なのか？
この論文の主定理はどういう結果なのか？
どれぐらいすごいのか？

ということに関して、私の理解できた内容をなるべく噛み砕いた上でご紹介したいと思います。

大変興奮する内容となっていますので、ぜひご覧になってください！

目次：

「星座」とは何か

数体の素元星座定理（主定理）

「数体の素元星座定理」のすごさ

定理1.6について

補足：プレプリントの正しさについて

「星座」とは何か

プレプリントの内容を紹介するにあたって、重要なキーワードは「星座（constellation）」です。ここではまず、テレンス・タオ（2006年）による「星座定理」を紹介したいと思います。テレンス・タオはフィールズ賞を受賞している超有名な数学者ですね。

通常の意味での素数とは、 $2, 3, 5, 7, \ldots$ のように、整数を素因数分解したときに出てくる数のことでした。整数は数直線の上に等間隔に並んだ点として表すことができます。今回考えたいのは、もう一つの軸である虚数軸を加えた複素数の世界です。複素数の実部と虚部がどちらも整数であるような数をガウス整数といいます。

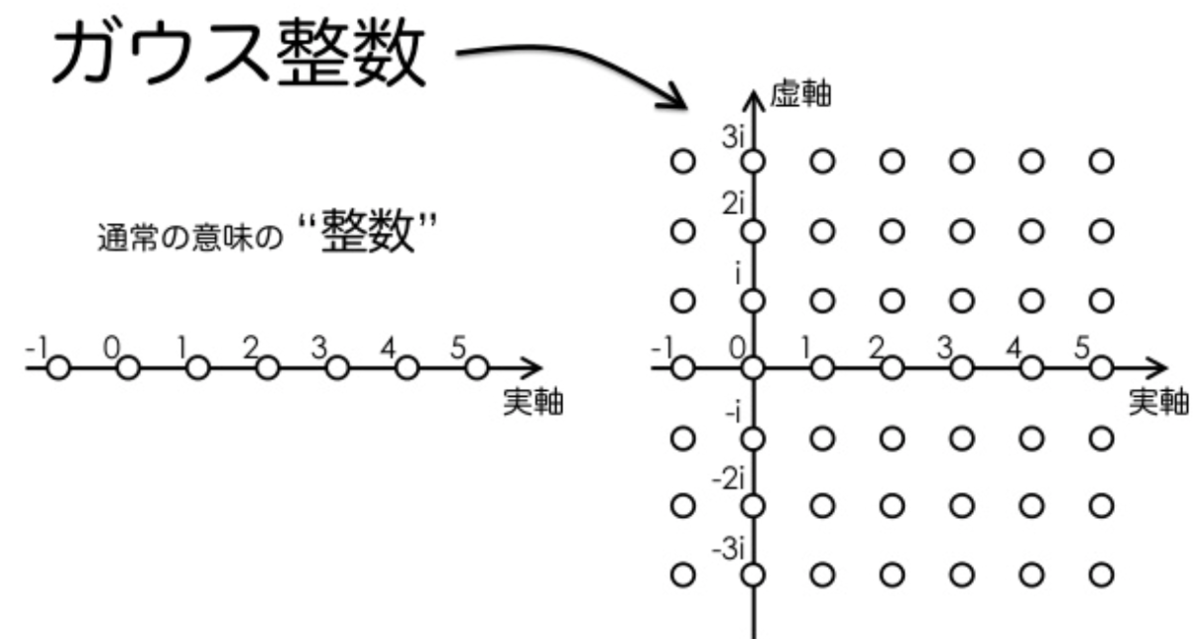
ガウス整数の中でも「素数的な存在」を考えることができて、これをガウス素数といいます。次の図の黒丸のところがガウス素数にあたります。

より正確に（通常の意味での）素数とは、 $\pm 1, \pm p$ 以外の整数で割り切れないような1を除く正の整数 $p$ のことです。

同様にガウス素数とは、 $\pm 1, \pm i, \pm p, \pm pi$ 以外のガウス整数で割り切れないような単数（ $\pm 1, \pm i$ ）を除くガウス整数 $p$ のことです。たとえば

$5+2i, \;\; 7, \;\; 3i$

といった数がガウス素数の一例ですね。

ガウス素数を黒い四角でプロットすると次のようになります：

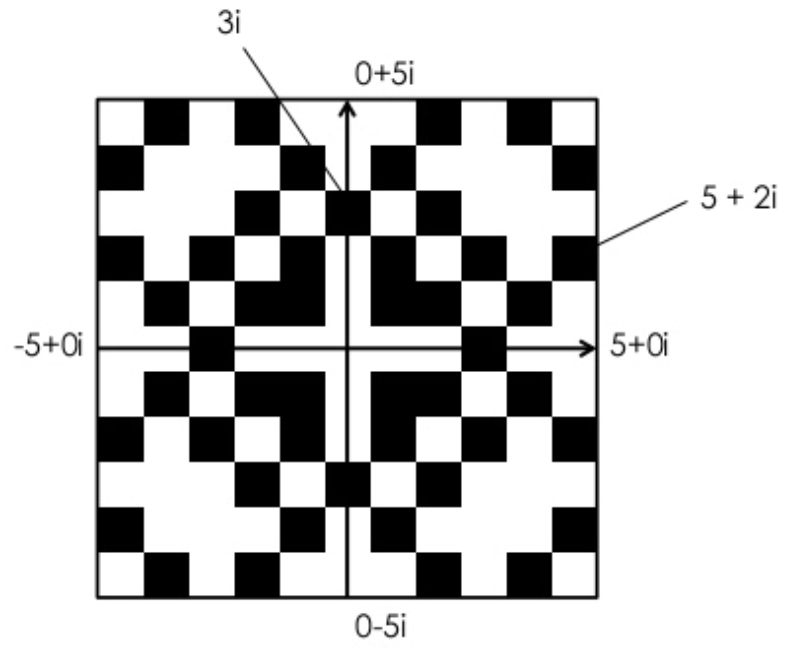
より広い範囲を調べてみると、次のようになります：

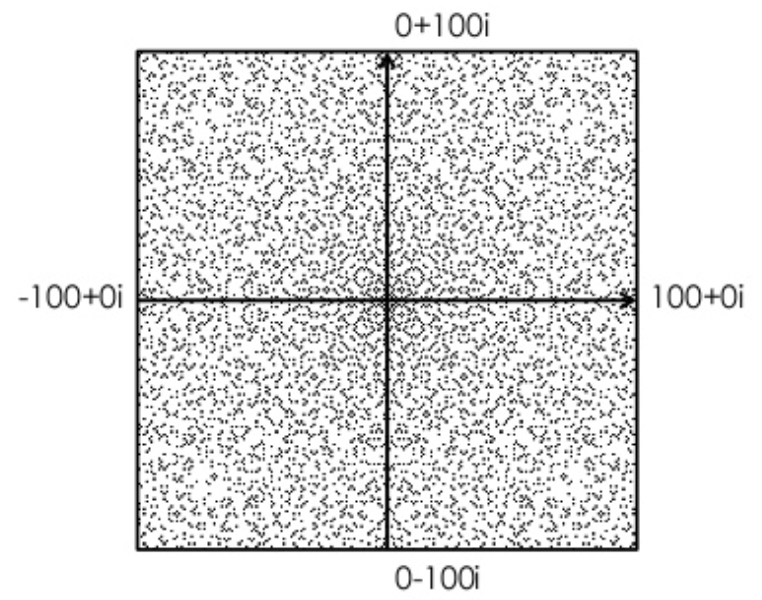
狭い範囲ではそれなりの密度でガウス素数が分布しているように見えますが、範囲を広げれば広げるほど、ガウス素数の分布は薄くなっていきます。

このガウス素数の各点をつないでできる図形が、今回の主役である「星座」という概念です。たとえば、図のような図形は星座です。

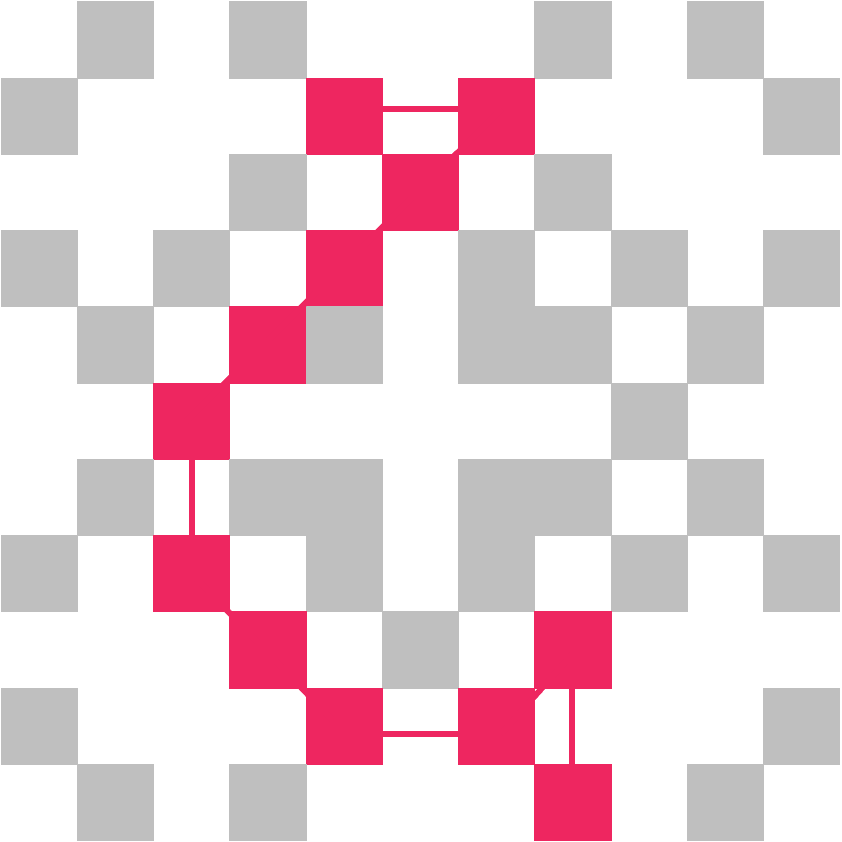
ガウス素数を１つの星と見立てて、星々を繋いで星座を作っているイメージですね。
（ちなみに、上の図はギリシャ文字の "ζ" をイメージして作った星座です。笑）

まず、有限個のガウス整数からなる集合のことを「形状」といいます。ある形状 $S$ が与えられたときに、 $S$ を拡大や平行移動して得られる集合を $S$ の「星座」といいます。

詳しい人向けの解説：
ガウス整数全体の集合 $\mathbb{Z}[i]$ は2次元の格子点で表せますので、これを $\mathbb{Z}^2$ と（ $\mathbb{Z}$ 加群として）同一視します。形状 $S$ は $\mathbb{Z}^2$ の有限な部分集合として定義されます。また、拡大・平行移動を次で定義します：

拡大・・・1以上の整数 $a$ に対して、 $aS := \{ ax \mid x \in S\}$ を $S$ の拡大という（ $ax$ は $x$ のすべての成分を $a$ 倍したもの）
平行移動・・・ $d \in \mathbb{Z}^2$ に対して、 $S+d = \{ x+d \mid x \in S\}$ を $S$ の平行移動という（ $x+d$ は $x$ と $d$ の各成分を足したもの）

ある1以上の整数 $a$ と $d \in \mathbb{Z}^2$ が存在して $aS + d$ と表される集合を星座と言います。

用語を定義したところで、天才数学者テレンス・タオが証明した驚くべき定理を紹介しましょう。

定理（ガウス素数の星座定理）

ガウス素数の集合には任意の形状の星座が無数に存在する

任意の形状に対して、その形状の「星座」であって、星座内のすべての点がガウス素数であるものが必ず存在するというのです。「任意の形状」ということは、あんな形状やこんな形状であっても、星座として存在するというわけです。

しかも、単に1つ存在するというだけでなく無数にです！「無数に」というのは要するに無限個存在するということです。これはやばいですね！

ある形状 $S$ を $n$ 個ならべた $S'$ を改めて形状とすると、 $S'$ の星座も存在することになります。したがって、任意の形状の星座が1個存在するのであれば、そこから無数に存在することが導かれます。少なくとも1個存在するというのが本質的なわけですね。

以前、日曜数学会というイベントにて、ガウス素数の星座定理について発表したことがありました。そのときは「おうし座」や「オリオン座」などのいくつかの「星座」の例を実際にガウス素数から探索して、それを紹介したりしました。
nico.ms

次のページでは、私が探した星座がガウス整数のどこにあるのかを実際に観察することができます。こうやって観察すると「任意の形状の星座が存在する」という驚くべき定理も、なんだか納得できそうな気がしてきます。
tsujimotter.info

数体の素元星座定理（主定理）

いよいよ、今回のプレプリントの主定理に話を進めたいと思います。

ガウス整数という「2次元の整数の世界」において、その素数全体という部分集合に対して「任意の形状の星座」が存在するという定理を紹介しました。このように聞くと、こんな一般化を考えたくなるかもしれません。

ガウス整数を $n$ 次元に一般化したような整数の世界において、その「素数」に対して「任意の形状の星座」は存在するか？

この問題にトライしたのが今回のプレプリントだったのです。「 $n$ 次元に一般化」と書いたところは、実際は「数体」という一般化を考えることになります。これについて前提となる最低限の概念を簡単に紹介しましょう。

なお、単に $n$ 次元に拡張するだけであれば、プレプリントのTheorem 1.2の直後にある (2) についての研究があります。これは、通常の意味での素数全体の集合 $P$ を $n$ 次元に並べた $P^n$ を考えて、 $P^n$ の相対密度が正である部分集合において任意の形状の星座が存在するという定理です。

この拡張は少し機械的な感じがする拡張ですが、今回のプレプリントによる拡張はより「自然」だと感じられるような定式化となっています。

有理数を係数とする $n$ 次の多項式 $f(x)$ の根（ $f(x) = 0$ の解のこと）となる複素数を代数的数といいます。

たとえば、1次方程式

$2x + 3 = 0$

の解 $x = -\frac{3}{2}$ は有理数ですが、これは代数的数です。

虚数単位 $i$ は $i^2 = -1$ ですから、 $f(x) = x^2 + 1 = 0$ の解となります。これも代数的数ですね。

代数的数 $\alpha$ を根に持つような次数最小の多項式を最小多項式といいます。

数体とは、有理数体 $\mathbb{Q}$ に代数的数 $\alpha$ を添加して得られる体 $\mathbb{Q}(\alpha)$ のことです。四則演算が滞りなく行える集合を体といい、 $\mathbb{Q}(\alpha)$ は $\mathbb{Q}$ と $\{\alpha\}$ の和集合を含む最小の体として定義されます。

$\alpha$ の最小多項式を $f(x)$ としたとき、 $f(x)$ の次数 $n$ を数体 $\mathbb{Q}(\alpha)$ の拡大次数と言います。このとき、 $\mathbb{Q}(\alpha)$ の任意の元は、 $n$ 個の有理数 $a_0, a_1, \ldots, a_{n-1}$ を用いて

$a_0 + a_1 \alpha + a_2 \alpha^2 + \cdots + a_{n-1} \alpha^{n-1}$

と表せます。 $\mathbb{Q}(\alpha)$ は、ちょうど $n$ 次元の（ $\mathbb{Q}$ 上の）ベクトル空間として表せるわけですね。

数体 $K = \mathbb{Q}(\alpha)$ の整数とは、 $n$ 次元のベクトル空間における格子点のような存在です。 $K$ の元 $\alpha$ であって、 $\alpha$ の最小多項式として最高次の係数が1である整数係数多項式を取れるものを $K$ の整数といいます。 $K$ の整数全体は環（足し算・引き算・掛け算ができる集合）をなし、これを $\mathcal{O}_K$ と表します。

抽象的な定義が続いたので具体例を示しますね。

有理数体 $K = \mathbb{Q}$ は、拡大次数は $1$ の数体と考えることができます。その整数環は $\mathcal{O}_K = \mathbb{Z}$ です。拡大次数は $1$ です。

ガウス数体 $K = \mathbb{Q}(i)$ は、 $i$ の最小多項式が $f(x) = x^2 + 1$ であるため、拡大次数は $2$ です。また、その整数は $a + bi$ （ $a, b$ は整数）という形の数全体であり、 $\mathcal{O}_K = \mathbb{Z}[i]$ と表します。これがガウス整数の集合です。ガウス整数は、2次元の格子点になっていましたね。

他にも2次元の例は無数に考えることができます。 $m \neq 0, 1$ を平方因子を持たない整数として $K = \mathbb{Q}(\sqrt{m})$ があります。 $\sqrt{m}$ の最小多項式は $f(x) = x^2 - m$ なので、拡大次数は $2$ です。その整数は $a+b\omega$ （ $a, b$ は整数）という形の数全体であり、 $\mathcal{O}_K = \mathbb{Z}[\omega]$ です。ここで $\omega$ は $m$ に応じて $\sqrt{m}$ か $\frac{1+\sqrt{m}}{2}$ となります。いずれにしても整数環 $\mathcal{O}_K$ は2次元の格子点として表せるわけです。

変わった例としては、 $K = \mathbb{Q}(\sqrt[3]{2})$ があります。 $\sqrt[3]{2}$ の最小多項式は $f(x) = x^3 - 2$ であり、拡大次数は $3$ です。その整数は $a + b\sqrt[3]{2} + c (\sqrt[3]{4})^2$ （ $a, b, c$ は整数）という形の数全体であり、 $\mathcal{O}_K = \mathbb{Z}[ \sqrt[3]{2} ]$ と表します。この場合は、3次元の格子点ですね。

他にも各 $n > 1$ について、拡大次数が $n$ であるような無数の数体が存在します。

一般に、数体 $K$ の拡大次数を $n$ としたとき、 $K$ は $n$ 次元のベクトル空間だと思うことができます。 $\mathcal{O}_K$ もまた $n$ 次元の格子点とみなせます。

また、一般の数体の整数環 $\mathcal{O}_K$ に対しても「素数」に相当する概念を定義することができて、それを素元といいます。

詳しい人向けの解説：
$\mathcal{O}_K$ には、素数の拡張として「素元」と「既約元」の2種類を考えることができますが、両者は異なる概念です。

一般に「素元」ならば「既約元」なので

$\{\text{素元}\} \; \subset \; \{\text{既約元}\}$

ということになります。ガウス素数は素元かつ既約元だったわけですが、星座定理を一般に拡張する上では、素元か既約元かのどちらを選ぶか検証する必要があります。素元だけで星座定理が成り立つならば、より強い定理ということになります。

実際、素元で十分だというのが、次の主定理の結果です。

さて、これにてプレプリントの主定理を述べる準備が整いました。

数体 $K$ の整数環 $\mathcal{O}_K$ に対して、ガウス整数のときと同様に $n$ 次元の形状 $S$ を定義します。ここで、 $\mathcal{O}_K$ の元を $n$ 次元の格子点とみなしています。これらを拡大したり、平行移動したりして得られる集合 $S'$ を $S$ の星座といいます。

このとき任意の形状に対して、 $\mathcal{O}_K$ の素元で構成される星座が存在するというのがプレプリントの定理の主張です。まさにガウス整数の星座定理の $n$ 次元への一般化というわけですね。

定理の主張を引用しましょう：

Theorem 1.3 (Constellation theorem in the prime elements of a number field). Let $K$ be a number field. Then there exist constellations of arbitrary shape in $\mathcal{O}_K$ consisting of prime elements of $\mathcal{O}_K$ .

日本語に訳すとこうなると思います：

定理1.3（数体の素元星座定理）

$K$ を数体とする。このとき、 $\mathcal{O}_K$ の任意の形状に対して $\mathcal{O}_K$ の素元によって構成される星座が存在する。

すばらしいですね！　こんなことが本当に成り立つとしたら、それはすごいことだと思うのです！

「数体の素元星座定理」のすごさ

とはいっても、ここまでの説明で「すごさ」はまだ十分伝わっていない気がするので、それをもう少しだけ説明したいと思います。

もっとも簡単なケースである $n = 1$ のとき、すなわち $K = \mathbb{Q}$ のとき、 $\mathcal{O}_K = \mathbb{Z}$ の星座定理を考えましょう。任意の形状を考えてよいので、 $S$ として

$S = \{0, 1, 2, \ldots, k-1\} \subset \mathbb{Z}$

というものも考えてよいでしょう。この $S$ を $a$ 倍し、 $d$ だけ平行移動させると

$aS + d = \{b, a+d, 2a+d, \ldots, (k-1)a+d\} \subset \mathbb{Z}$

となります。これは初項 $d$ 、公差 $a$ であるような長さ $k$ の等差数列ということになります。

この長さ $k$ の等差数列がすべて素数によって構成されるような $a, d$ が存在するといっているわけですね。これは、

素数からなる任意の長さの等差数列が存在する

ことを意味します。これはグリーン・タオの定理と呼ばれる大定理です。

本当は、上で得られた $aS + d$ が（ $-$ 素数）の形の数を含む可能性も考える必要があります。しかしながら、簡単な議論により（正の）素数のみからなる等差数列の存在が言えます。

たとえば、

$3, 5, 7$

$5, 11, 17, 23, 29$

は、どちらも素数からなる等差数列であり、それぞれ長さ3, 5のものです。他にも、コンピュータを使って、素数からなる長さ27までの等差数列が2019年に発見されているそうです。しかしながら、グリーン・タオの定理は、素数からなる任意の長さの等差数列があると主張しているわけですね。

グリーン・タオの定理の証明は、それ自体大変難しいものです。そのような大定理を一番簡単なケースとして含んでいるわけですね。

興味がある方は、関さんご自身によるMathpowerの講演をご覧ください。グリーン・タオの定理のすごさがわかるかと思います。
www.nicovideo.jp

元々、関さんはこの分野の研究者ではなかったようですが、2017年のMathpowerに向けて尋常ではない熱意のもと勉強されていました。その結果として上記の素晴らしい講演となったわけですね。また、この講演がきっかけとなり今回の研究に繋がったとのことです。

グリーン・タオの定理を $K = \mathbb{Q}$ の定理と見たときに、 $K = \mathbb{Q}(i)$ に対する定理がテレンス・タオによるガウス素数の星座定理です。

ここまででも十分難しい問題というわけですが、さらに数体 $K$ に一般化することは、素人目にも簡単なことではなさそうに思います。実際、よく知られていることとして、一般の数体の整数環 $\mathcal{O}_K$ において素因数分解（正確には既約元分解）の一意性は保たれません（UFDではない）。単数群も複雑になります。

タオ自身も数体への一般化を構想していたようですが、「少なくとも整数環がUFDかつ単数群が有限群（10個しかない）の場合には証明できるだろう」と予想していたようです。

今回のプレプリントでは、その条件の一切を取っ払って、任意の数体に対して星座定理を示してしまったと主張しています。これはとんでもないことだとは思いませんか！！

実は、今回のプレプリントでは、上で紹介した定理1.3の結果をさらに強めることに成功しています。それが系1.5です。これもこのプレプリントのすごさの一つだと思います。

Corollary 1.5. In the statement of Theorem 1.3, we can take constellations that do not admit associate pairs.

系1.5

定理1.3の主張において、同伴のペアを持たない星座を選ぶことができる。

これはどういう主張か説明しましょう。

整数環には単数と呼ばれる数が存在します。整数の場合 $\pm 1$ 、ガウス整数の場合 $\pm 1, \pm i$ です。 $1$ のような数だと思っていただければと思います。ある数 $a$ に単数 $u$ を掛けてできる数 $au$ を考えたとき、 $a$ と $au$ は同伴であるといいます。

単数の個数が小さい場合はあまり気にならないかもしれませんが、たとえば $\mathbb{Z}[\sqrt[3]{2}]$ の場合は $\varepsilon_0 = 1 + \sqrt[3]{2} + (\sqrt[3]{2})^2$ を基本単数として $\varepsilon^{n}$ （ $n$ は整数）と書ける数がすべて単数となります。無限に単数があるわけですね。つまり、一つの数 $a$ に対して同伴な数は無限に存在するわけです。

したがって、単数が十分に多い場合は、一つの数を使って同伴な数をたくさん作り、その数を使って星座を構成できてしまうかもしれません。これは少し「ずるい」感じがします。

しかしながら、上の系1.5は同伴なペアを一切含まないような星座を取ることができるといっていて、定理1.3より強い結果になっていることがわかりますね。実際、定理1.4が肝になっていて、これによって強い主張をいうことができるようです。

もちろん、私は証明の一切をまだ読めてはいないので、技術的な部分については何も知りません。細部まで理解することができたら、より深い感動を味わえるのだと思います。しかしながら、定理の主張だけでもこれだけ感動できるというのは、なかなかないことだと思います。

個人的には、関さんとは以前から親しくさせていただいており、尊敬すべき数学者であり、なおかつ日曜数学の仲間だと思っています。そのため、今回の結果を知って、感慨深い気持ちです。2016年の数学カフェで一緒に講演したときに、グリーン・タオの定理の主張を教えていただきました。その頃は、関さん自身はグリーン・タオの定理については、まだ十分に理解できていないと話していた記憶があります。その後、Mathpowerの講演を準備しているところも、ブログを通して見てきました。その熱意は本当に鬼気迫る感じで、講演でもその熱量に圧倒されました。あのときの講演がこのような形で味を結んだのですね。本当に嬉しく思います。

定理1.6について

上で説明した定理1.3・系1.5だけでも十分味わい深いのですが、プレプリントにはもう一つ面白い結果（定理1.6）が載っています。最後にそれを味わってから終わりにしたいと思います。

定理1.6（2元2次形式の表現する素数に関する星座定理）

$F\colon \mathbb{Z}^2 \to \mathbb{Z}$ を原始的な2次形式とする。また、 $F$ の判別式 $D_F$ は完全平方数ではないとし、 $F$ は負定値ではないとする。このとき、与えられた有限集合 $S\subset \mathbb{Z}^2$ に対して、 $S$ の星座 $\mathcal{S}$ が $\mathbb{Z}^2$ 内に存在して、関数 $F(x, y)$ は $\mathcal{S}$ 上で相異なる素数の値をとる。

この定理1.6は 2次形式の表現する素数に関する定理です。

次の記事で「2次形式の表現する素数」に関する記事を書いていますので、この分野に興味がある方はぜひご覧になってください。
tsujimotter.hatenablog.com

2次形式とは

$x^2 + y^2$

$2x^2 + 2xy + 3y^2$

のような式のことです。どちらもすべての項の次数が「ちょうど2」となっていますね。

一般の（2元）2次形式は、整数 $a, b, c$ を用いて

$F(x, y) = ax^2 + bxy + cy^2$

と表せる式として定義されます。整数 $x, y$ によって素数 $p$ が $p = F(x, y)$ と書けるとき、 $p$ は $F$ によって表現されるといいます。

2次形式によって表現される素数の法則は、古くから数学者の興味を掻き立ててきました。

フェルマーは $p = x^2 + y^2$ と表せる素数の必要十分条件は $p = 2$ または $p \equiv 1 \pmod{4}$ であることを発見しました。

ラグランジュは、 $p\neq 2, 5$ であるような素数に対して

$\begin{align} p = x^2 + 5y^2 \;\; &\Longleftrightarrow \;\; p \equiv 1, 9 \pmod{20} \\ p = 2x^2 + 2xy + 3y^2 \;\; &\Longleftrightarrow \;\; p \equiv 3, 7 \pmod{20} \end{align}$

が成り立つことを示しました。

こんな風に2次形式で表せる素数 $p$ の法則が、 $p$ を $N$ で割ったあまりで表せるというのが大変興味深いです。もちろん、法則が「 $N$ で割ったあまり」で表せないものもあって、これがまた面白いのですが。

ここまでが古典的な結果です。定理1.6では、2次形式について $F(x, y)$ が素数を表現するような $(x, y)$ 全体の集合 $A$ について考えています。

たとえば、 $F(x, y) = x^2 + 5y^2$ が素数を表現するような $(x, y)$ の集合は、次の図の左側になります。

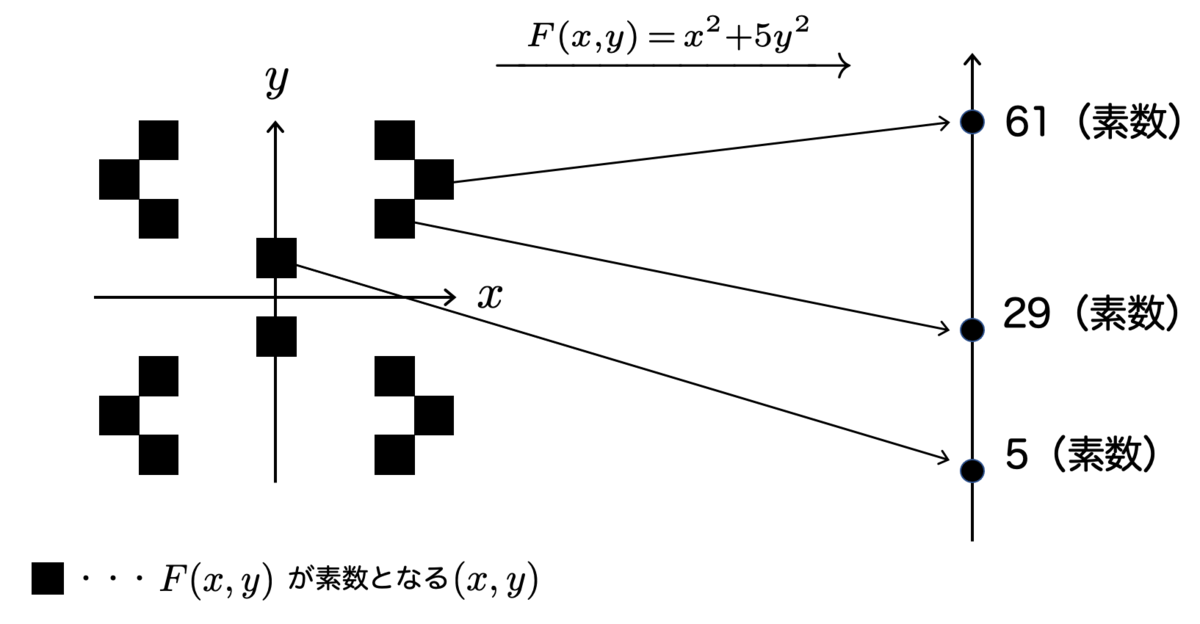
このような集合 $A$ で構成されるような2次元の星座が存在するかどうかを考えたいと思います。

定理1.3との関係を述べましょう。2次形式 $F(x, y) = x^2 + y^2$ を考えます。素数 $p$ がこの $F(x, y)$ によって表現されるとき

$p = x^2 + y^2 = (x + yi)(x - yi)$

と分解され、右辺はガウス整数の共役な積になっています。したがって、このような素数 $p$ はガウス整数の集合 $\mathbb{Z}[i]$ においてガウス素数の積に分解されるということですね。 $F(x, y)$ によって表現される素数を分解して得られるガウス素数全体は、ガウス素数全体の部分集合になります。このように考えると、2次元の星座定理の拡張になっていると思えます。

また、2次形式 $F(x, y) = x^2 + 23y^2$ を考えると、これは

$x^2 + 23y^2 = (x + y\sqrt{-23})(x - y\sqrt{-23})$

のように分解されますが、これは環 $\mathbb{Z}[\sqrt{-23}]$ を考えていることになります。

ところで、 $\mathbb{Q}(\sqrt{-23})$ の整数環（極大整環）は $\mathbb{Z}\left[\frac{1+\sqrt{-23}}{2}\right]$ でしたから、この場合は整数環と一致しません。つまり、整数環とは限らない一般の整環も視野に入れた問題設定というわけですね。拡張になっているわけです。

その上で同様に2次元の星座を定義したときに、星座定理が成り立つかどうか考えたいと思います。

いくつか細かな仮定を入れます。

素数を表現するためには、 $F(x, y) = ax^2 + bxy + cy^2$ の係数 $a, b, c$ の最大公約数が1である必要があります。最大公約数が1より大きな $d$ であるとすると、表現されるすべての数が $d$ で割り切れてしまうからです。このような2次形式を原始的（primitive）といいます。

また、判別式 $b^2 - 4ac$ が完全平方数（perfect square）ではない、負定値（negative definite; $F(x, y)$ が負の値しか表現しない）ではないという条件も仮定します。

これらは当然仮定すべき条件というものであって、特殊な条件では全くないことに注意しましょう。

このように設定した上で

（上記の仮定を満たす）任意の2次形式に対して星座定理が成り立つ

というのが定理1.6の主張です。すなわち、形状 $S \subset \mathbb{Z}^2$ （有限集合）に対して、 $S$ の拡大・平行移動して得られる星座 $\mathcal{S} \subset A$ が存在するというわけです。

これはすごいですね！

しかも！！

このとき星座 $\mathcal{S} \subset A$ が表現する素数はすべて異なる素数になります！！！

おおお、面白い！！！

実際、こんなことが成り立つのか、具体例で確認してみましょう。

2次形式として $F(x, y) = x^2 + 23y^2$ を考えて、 $F(x, y)$ が素数を表現する $(x, y)$ 全体の集合を $A$ としましょう。

また、形状 $S$ として7点集合「北斗七星」を考えます。

$S$ を拡大・平行移動して得られる星座 $\mathcal{S}$ であって、 $A$ に含まれるものを探しましょう。

実際、 $-90 \leq x \leq 90, \;\; -90 \leq y \leq 90$ の範囲で探すと、次のような星座が見つかりました！

ちょっと見辛いかもしれませんが、グレーの点が $A$ の点、赤い点が見つけた星座 $\mathcal{S}$ です。せっかくなので $\mathcal{S}$ の座標も表示しておきましょう。

$\mathcal{S} = \{(40, -21), \; (52, -27), \; (58, -33), \; (64, -39), \; (64, -45), \; (76, -51), \; (82, -45)\}$

ここで、 $\mathcal{S}$ によって $F(x, y)$ が表現する素数を計算すると

$\{11743, \; 19471, \; 28411, \; 39079, \; 50671, \; 65599, \; 53299\}$

となります。たしかに、どれも相異なる素数となっていますね！！

いやー、面白いな！！

補足：プレプリントの正しさについて

最後になりますが、念のために論文の正しさということについて、一点注意を述べておきたいと思います。

学術論文というのは、一般に論文誌に投稿され、数名の査読者によって内容が十分に精査されてから論文誌として出版されます。この過程によって、内容の正しさが一定程度保証されるわけですね。もちろん、査読をクリアしたからといって証明が正しいと保証されているわけではなく、出版後もさまざまな研究者によって検証されていくわけです。

今回のものは、論文誌に投稿前（あるいは査読中）の原稿を事前公表する「プレプリント」と呼ばれるものであり、まだ査読が入っていない原稿です。したがって、（著者が万全のチェックをした上で出していることは仮定してよいとは思いますが）十分に正しさが保証されたものとはいえません。内容の正しさは、あくまで読者自身が確認することが前提というわけですね。

そのため、まだプレプリントの段階の内容を紹介する際には、その点を十分に配慮する必要があると考えています。今回の記事について述べておくと、数体の素元星座定理が「証明された」とは一切書いておりません。