指数層系列(1)：指数関数の性質から得られる短完全列

今日の記事は３回に渡るシリーズ記事の第１回です。シリーズを通して、複素数の変数を持つ指数関数

$\displaystyle \exp(x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \left(= \sum_{n=0}^{\infty} \frac{x^n}{n!} \right) \tag{1}$

に関連する「指数層系列」と呼ばれる概念について紹介したいと思います。

指数層系列シリーズの記事は、こちらのタグから読むことができます：
tsujimotter.hatenablog.com

指数層系列は、層の間の準同型がなす完全列です。その完全列が成立する背景には、指数関数の持つ素朴な３つの性質（指数法則・対数関数・周期性）があります。高校のときに習った指数関数が、層という高度な概念に繋がっていくというのはとても興味を引き立てるものがあります。

最終的には指数層系列まで行きたいのですが、今回はその前の準備段階として、指数関数の性質から導ける短完全列を２つほど紹介したいと思います。

記号の定義と前提知識
複素数全体の集合を $\mathbb{C}$ と表し、0でない複素数全体の集合を $\mathbb{C}^{\times}$ と表します。

また、 $\mathbb{C}$ の任意の開集合 $U$ に対し、 $U$ 上の正則関数全体の集合を $\mathcal{O}(U)$ とし、 $U$ 上の「至るところ 0 でない」正則関数全体の集合を $\mathcal{O}(U)^\times$ とします。

また、今回の記事では、正則関数や対数関数の多価性についての知識を前提とします。自信がない方はこちらの記事を読んでいただけると嬉しいです。
tsujimotter.hatenablog.com

目次：

1. 指数関数は 0 にならない

2. 正則関数の間の完全列

まとめ

参考文献

1. 指数関数は 0 にならない

指数関数を特徴付ける重要な性質に

$\begin{align} \exp(x+y) &= \exp(x) \exp(y) \\ \exp(0) &= 1 \end{align} \tag{2}$

がありました。高校生のときに当たり前に習った指数法則ですが、ここからいくつか重要な性質が導かれます。

まず、指数関数は「至るところ 0 にならない」ことが導かれます。 $y = -x$ を代入すると

$\displaystyle \exp(x)\exp(-x) = 1$

となります。すなわち、 $\exp(x)$ は逆元 $\exp(-x)$ を持つことがわかり、至るところ0にならないとわかります。

したがって、0を除く複素数全体を $\mathbb{C}^\times$ とすると

$\begin{align} \exp \colon \mathbb{C} &\longrightarrow \mathbb{C}^\times \\ x &\longmapsto \exp(x) \end{align} \tag{3}$

という写像が得られるわけです。

また指数法則 $(2)$ より、式 $(3)$ の写像が「アーベル群の準同型写像」であることが次のようにわかります。

複素数 $\mathbb{C}$ は足し算に対して群をなします。また、0でない複素数は掛け算に対して群をなします。どちらも交換法則がなりたつので、アーベル群です。

$x, \; y \in \mathbb{C}$ のとき $x+y\in\mathbb{C}$

$x, \; y \in \mathbb{C}^\times$ のとき $xy\in\mathbb{C}^\times$

定義域 $\mathbb{C}$ と値域 $\mathbb{C}^\times$ に上の演算を入れて群構造を考えたときに、指数関数は群の演算を保つ準同型写像になっているというのが式 $(2)$ の意味するところです。

$\begin{align} \exp \colon \mathbb{C} &\longrightarrow \mathbb{C}^\times \\ x &\longmapsto \exp(x) \\ y &\longmapsto \exp(y) \\ x+y &\longmapsto \exp(x)\exp(x) \\ 0 &\longmapsto 1 \end{align}$

アーベル群の準同型写像 $\exp\colon \mathbb{C} \to \mathbb{C}^\times$ を得たわけなのですが、この写像 $\exp$ は全射であることがわかります。証明のキーは、対数関数 $\log$ の存在です。

任意の $y \in \mathbb{C}^\times$ に対して、 $x \in \mathbb{C}$ を $\log(y)$ の主値とすれば $y = \exp(x)$ を満たします。したがって、任意の $y \in \mathbb{C}^\times$ に対して、 $y = \exp(x)$ なる $x \in \mathbb{C}$ の存在が言えました。

また、 $\exp$ が単射でないこともわかります。それは $\exp$ の周期性（あるいは $\log$ の多価性）からわかります。

実際

$\exp(x) = 1$

となるような $x \in \mathbb{C}$ は、 $x = 2\pi i n \;\; (n \in \mathbb{Z})$ という形に限ることがわかります。

すなわち

$2\pi i \mathbb{Z} := \{ 2\pi i n \mid n \in \mathbb{Z} \}$

とおけば、 $\operatorname{Ker}(\exp) = 2\pi i \mathbb{Z}$ と表すことができます。また、 $2\pi i \mathbb{Z}$ は足し算についてアーベル群をなし、 $\mathbb{C}$ の部分群です。

以上の事実を「完全列」という言葉ですっきりまとめることができます。

「完全列」という概念に慣れていない人に向けて、少しだけ説明しておきます。一般に

$\cdots \longrightarrow A \xrightarrow{\;f\;} B \xrightarrow{\;g\;} C \longrightarrow \cdots \tag{4}$

なるアーベル群と準同型の列があり

$\operatorname{Ker}(g) = \operatorname{Im}(f)$

が成り立つとき、式 $(4)$ の列は $B$ で完全であるといいます。式 $(4)$ の列のすべての対象について完全であるとき、 $(4)$ は完全列であるといいます。完全列が

$0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$

という形をしているとき、短完全列であるといいます。

先の議論を踏まえて、次のような短完全列が得られます：

$0 \longrightarrow 2\pi i \mathbb{Z} \xrightarrow{\;\;i\;\;} \mathbb{C} \xrightarrow{\exp} \mathbb{C}^\times \longrightarrow 0 \tag{5}$

ここで $i$ は、 $2\pi i \mathbb{Z}$ の $\mathbb{C}$ への埋め込み写像です。

さて、式 $(5)$ が短完全列であることは、定義にしたがって左から順に確認すればよいでしょう。

$\begin{align} \operatorname{Ker}(2\pi i \xrightarrow{i} \mathbb{C}) &= \operatorname{Im}(0 \rightarrow \mathbb{C}) \;\;\;\; (= 0) \\ \operatorname{Ker}(\mathbb{C} \xrightarrow{\exp} \mathbb{C}^\times) &= \operatorname{Im}(2\pi i \xrightarrow{i} \mathbb{C}) \\ (\mathbb{C}^\times = ) \;\;\;\; \operatorname{Ker}(\mathbb{C}^\times \rightarrow 0) &= \operatorname{Im}(\mathbb{C} \xrightarrow{\exp} \mathbb{C}^\times) \end{align}$

これらの条件は、それぞれ次のことを表しています。

１番目の条件は $i$ が単射であること
２番目の条件は $\exp$ の核 $\operatorname{Ker}(\mathbb{C} \xrightarrow{\exp} \mathbb{C}^\times)$ が $2\pi i \mathbb{Z}$ であること
３番目の条件は $\exp$ が全射であること

指数関数の持つ重要な情報を、完全性によって簡潔に表現しているわけですね。

このような完全列が今日の主役です。

2. 正則関数の間の完全列

上の完全列と同じような考え方を応用すると、もう一つ興味深い完全列を得ることができます。今度の完全列における対象は「正則関数全体の集合」です。

$\mathbb{C}$ 上の任意の開集合を $U$ とします。 $U$ 上の正則関数全体の集合を $\mathcal{O}(U)$ と表し、その中で特に「至るところ0にならない」正則関数全体の集合を $\mathcal{O}(U)^\times$ と表すことにします。

$\mathcal{O}(U)$ は環をなすことがわかり、特に加法についてアーベル群をなすことがわかります。このときの $f, g \in \mathcal{O}(U)$ に対する加法の演算 $f + g$ は、任意の $x \in U$ に対して

$(f+g)(x) = f(x) + g(x)$

が成り立つこととして定義されます。 $f, g \in \mathcal{O}(U)^\times$ に対する乗法 $fg$ も、同様に任意の $x \in U$ に対して

$(fg)(x) = f(x)g(x)$

が成り立つこととして定義されます。

乗法に対して逆元を持つことは、至るところ0にならないことと同値（逆数をとったときに分母が0にならない）なので、 $\mathcal{O}(U)^\times$ は乗法に対してアーベル群をなします。

ここでは、前節のように $\mathcal{O}(U), \; \mathcal{O}(U)^\times$ の間の準同型写像を考えたいと思います。任意の正則関数 $f \in \mathcal{O}(U)$ をとったときに、 $\exp$ と $f$ の合成 $\exp \circ f$ を考えます。

すなわち、合成 $\exp\circ f$ は任意の $x \in U$ に対して

$(\exp \circ f)(x) = \exp( f(x) )$

として定義されます。

すると

$\begin{align} \exp \colon \mathcal{O}(U) &\longrightarrow \mathcal{O}(U)^\times \\ f \;\;\;&\longmapsto \exp \circ f \end{align} \tag{6}$

という写像が得られることが、次のようにしてわかります。

微分すると

$\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}(\exp \circ f)(x) = \exp( f(x) ) \frac{\mathrm{d}f}{\mathrm{d}x}$

より、合成関数 $\exp\circ f$ も $U$ 上の正則関数となります。

さらにいえば、 $\exp$ は至るところ0にならない関数なので、 $\exp\circ f$ も至るところ0にならない関数であることがわかります。したがって、 $\exp\circ f \in \mathcal{O}(U)^\times$ です。

また、 $f, g \in \mathcal{O}(U)$ は、任意の $x$ に対して

$\exp( (f+g)(x) ) = \exp( f(x) + g(x) ) = \exp( f(x) ) \exp( g(x) )$

を満たしますから

$\exp \circ (f+g) = (\exp \circ f) (\exp \circ g)$

です。すなわち、式 $(6)$ の写像はアーベル群の準同型写像です。

このようにして得られた準同型写像について、前節と同じような完全列が成り立つかどうか考えたいと思います。ただし、ここから先は任意の開集合 $U$ を考えるのではなく、 $U$ としては連結な領域を考えたいと思います。

私はいつも「連結」と「単連結」という用語の違いで混乱するので、まとめて図で表しておきたいと思います。

f:id:tsujimotter:20191217131207p:plain:w500

要するに繋がっていたら「連結」で、繋がっていてかつ穴が空いていなければ「単連結」です。

$U$ は連結という条件で $\exp( f(x) ) = 1$ になるような正則関数 $f \in \mathcal{O}(U)$ を考えます。

まず、前節の議論により $\operatorname{Ker}(\mathbb{C} \xrightarrow{\exp} \mathbb{C}^\times) = 2\pi i \mathbb{Z}$ です。したがって

$f\colon U \longrightarrow 2\pi i \mathbb{Z}$

となります。 $U$ の連結性と $f$ の連続性より、 $f$ が定数関数であることが言えて

$f(x) = 2\pi i n \;\; (n \in \mathbb{Z})$

という形に限ることがわかります。

f:id:tsujimotter:20191217140111p:plain:w360

したがって

$\operatorname{Ker}(\mathcal{O}(U) \xrightarrow{\exp} \mathcal{O}(U)^\times) = 2\pi i \mathbb{Z}$

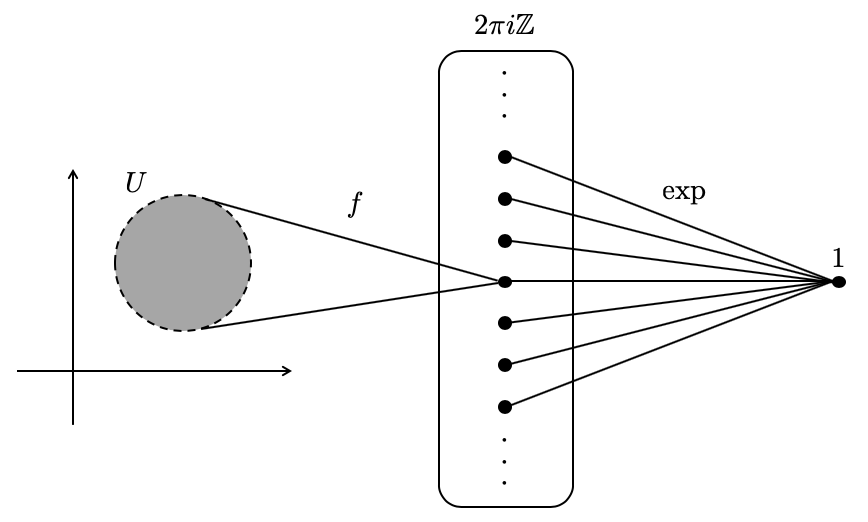
ということです。この場合の $2\pi i \mathbb{Z}$ の元は、 $U$ 上の正則関数であるような定数関数だと思っています。

以上の議論により、任意の連結な開集合 $U \subset \mathbb{C}$ に対して、次の完全列が得られます。

$0 \longrightarrow 2\pi i \mathbb{Z} \xrightarrow{\;\;i\;\;} \mathcal{O}(U) \xrightarrow{\exp} \mathcal{O}(U)^\times \tag{7}$

ほとんど、式 $(5)$ と同じような形の完全列が得られていて、面白いですね。

今は、 $U$ として連結なものだけを考えています。つまり、連結成分が1個ということですね。

一方で連結成分が2個以上の場合は、 $\exp( f(x) ) = 1$ なる $f$ としては、連結成分ごとに異なる $2\pi i \mathbb{Z}$ の値を対応させてもよいとわかります。

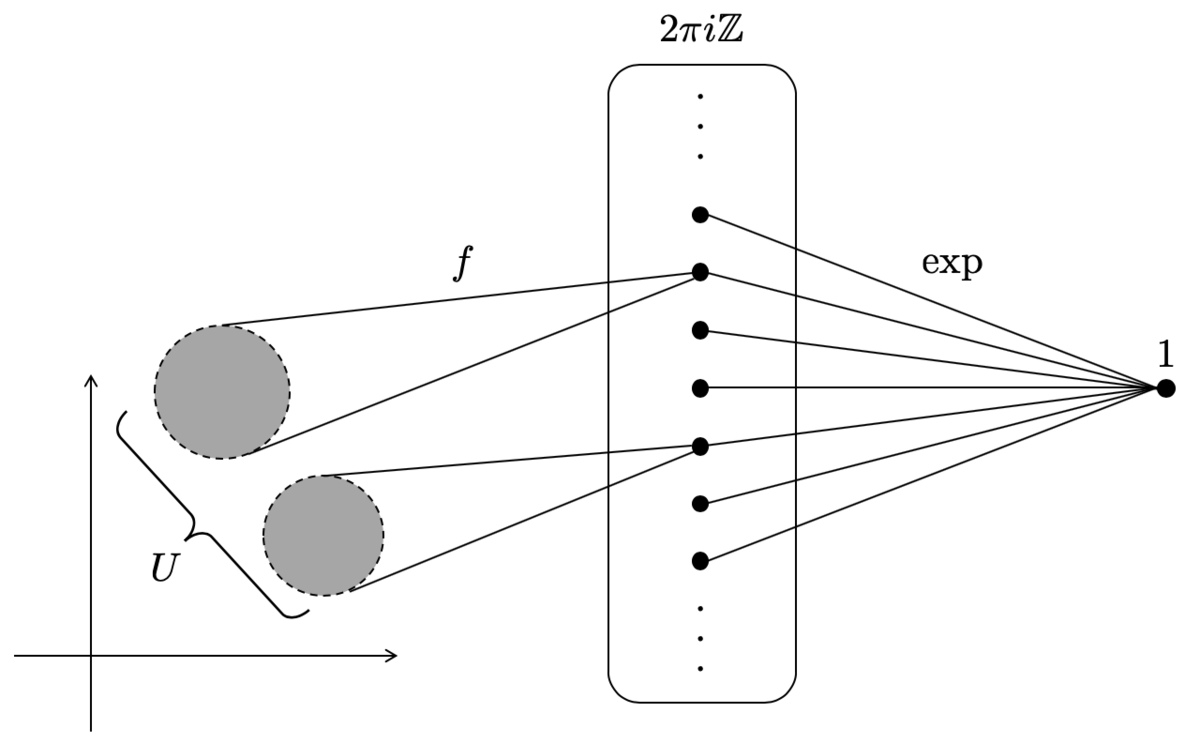
f:id:tsujimotter:20191217140648p:plain:w360

したがって、 $U$ が連結ではないとき、 $U$ の連結成分の個数を $r$ とすると

$0 \longrightarrow 2\pi i \mathbb{Z}^{\oplus r} \xrightarrow{\;\;i\;\;} \mathcal{O}(U) \xrightarrow{\exp} \mathcal{O}(U)^\times$

が成り立つことになりますね。このことは、次回「定数層」の話をする際に、もう一度触れたいと思います。

ところで、完全列 $(7)$ と完全列 $(5)$ の違いを考えると、完全列 $(7)$ の最後が $0$ ではないことが気になりますね。これは、 $\mathcal{O}(U) \xrightarrow{\exp} \mathcal{O}(U)^\times$ の全射性が示せていないことによります。

結論から言うと

$U$ が単連結であることが、 $\exp$ が全射であることの必要十分条件

となります。

「 $U$ は単連結 $\Longrightarrow \; \exp$ は全射」の証明については、少し難しいので今回は扱いません。次回登場する「指数層系列」や、その次に扱う「層係数コホモロジー」によってスッキリ解決できますので、またそのときに議論することにします。

ここでは、「 $\exp$ は全射 $\Longrightarrow \; U$ は単連結」の対偶として、単連結ではない開集合 $U$ に対して、全射性が成り立たないことを示しましょう。

単連結でない開集合 $U$ を考えます。 $U$ は単連結ではないので、少なくとも一つ以上の穴が空いています。穴の中の一点として $a \in \mathbb{C}$ を考えます。

f:id:tsujimotter:20191219085403p:plain:w200

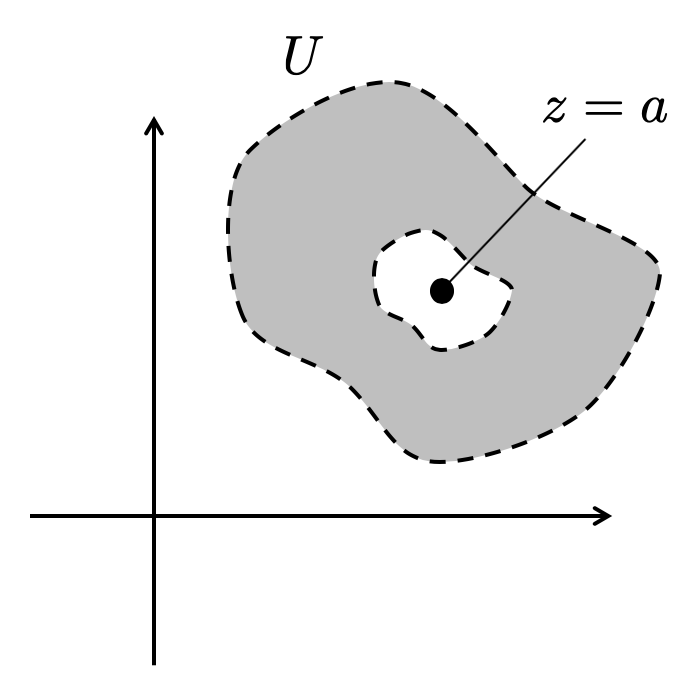
このとき、 $U$ 上の至るところで 0 にならない正則な関数として $g(z) = z - a$ があります。

$g(z) = z - a$ が 0 になるのは $z = a$ に限りますが、 $z = a$ は $U$ の外側にあるので問題ありません。よって、 $g \in \mathcal{O}(U)^{\times}$ です。

$g$ に $\log$ を合成した $f = \log \circ g$ を考えましょう。この関数は $z \in U$ に対して

$f(z) = \log( g(z-a) ) = \log(z-a)$

になるので、これは原点を $z = a$ にずらした対数関数ですね。

今、定義域 $U$ においては、 $z = a$ の周りを1周する経路がとれます。（そもそも、それが単連結ではないことの定義でした。）

f:id:tsujimotter:20191219085345p:plain:w200

そのように1周させて元の位置に戻ると、 $f(z)$ は異なる値をとってしまいます（「iのi乗はそこに至る経路で決まる」の議論を思い出しましょう）。すなわち、 $f$ は $U$ 上の多価正則な関数です。したがって、 $f\not\in \mathcal{O}(U)^\times$ となります。

今までの議論により「単連結でない $U$ では、ある $g \in \mathcal{O}(U)^\times$ が存在して $g = \exp \circ f$ なる $U$ 上の正則関数 $f$ が存在しないこと」を示せました。すなわち、「 $U$ は単連結でない $\;\; \Longrightarrow\;\; \mathcal{O}(U) \xrightarrow{\exp} \mathcal{O}(U)^\times$ は全射ではない」が示せたというわけです。