12 = 3×4, 56 = 7×8シリーズの第4弾。まさか続くと思っていませんでした。
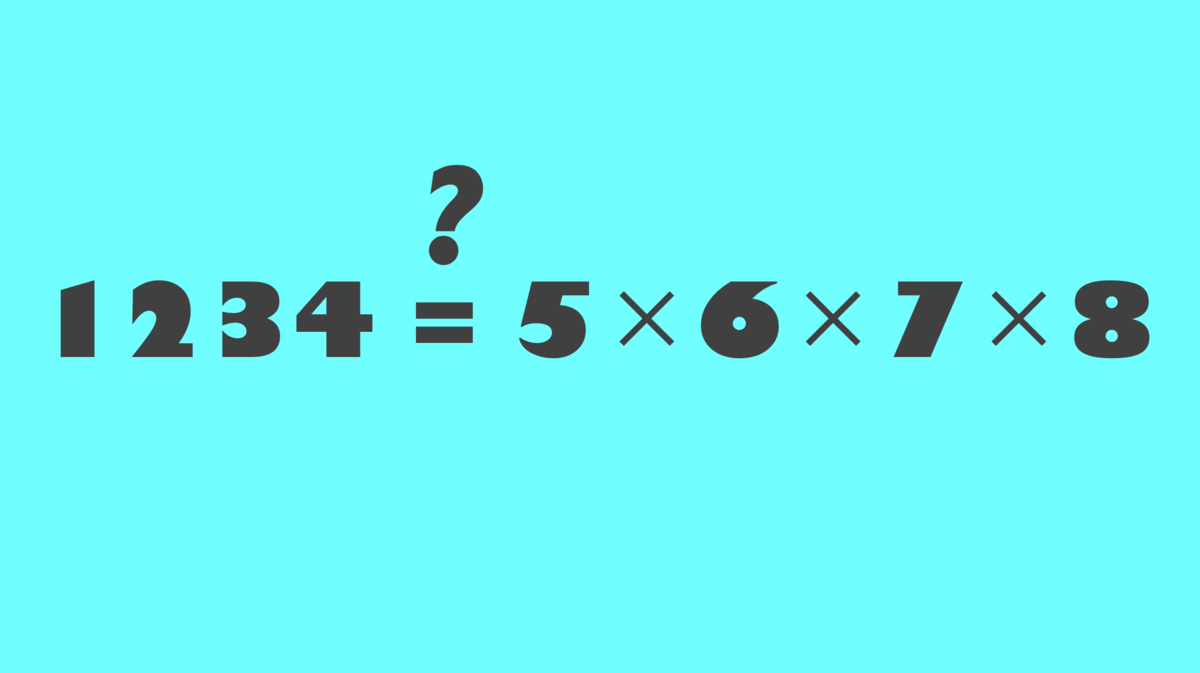
シリーズの記事は「12 = 3×4, 56 = 7×8」というタグでまとめていますので、よろしければご覧になってください。
tsujimotter.hatenablog.com
今日のテーマ
前回までの記事を公開したところ、二世さん(@m_2sei)から
まさか、この先の問題が解けるとは思っていなかったので驚きです。許可をいただいてその解法を紹介したいと思います。
というわけで、今回の問題はこちらです。
このとき、 の組を求めよ。
次数がだいぶ増えてきたので、いかにも難しそうですが、やってみましょう。
解法
基本的には、みうらさんによる3-3のパターン(左辺が3桁、右辺が3つ積のパターン)の解法の通りに進めていきます。
tsujimotter.hatenablog.com
まず なので、正の整数
を用いて
と表すと
となることがわかります。
その を用いて、式
に
を代入します。
これで、変数は だけになりました。
さらに式 の(左辺)
(右辺)を、関数
で表すことにします。
となるような
が元の問題の解を与えるというわけです。
ここで のとき、
は実際には正の値をとってしまう、という補題を示したいと思います。すなわち、この条件では解がないということです。
ここで、 は
についての 3次関数 になっていることに注意します(4次の項が消えた!)。
のとき、
の3次、2次、1次の項の係数はそれぞれ
となることがわかります。したがって、 は
のとき 単調増加 します。
ここで のとき、
を計算すると
となります。
したがって、 が言えました。(補題の証明終わり)
以上により、 として考えるべき範囲は
のとき、すなわち
の 3通り を調べればよいでしょう。
 のとき
のとき
を代入すると
となります。 で微分すると
であり、 より
が のグラフの極値となります。よって、
は
の範囲で単調増加します。
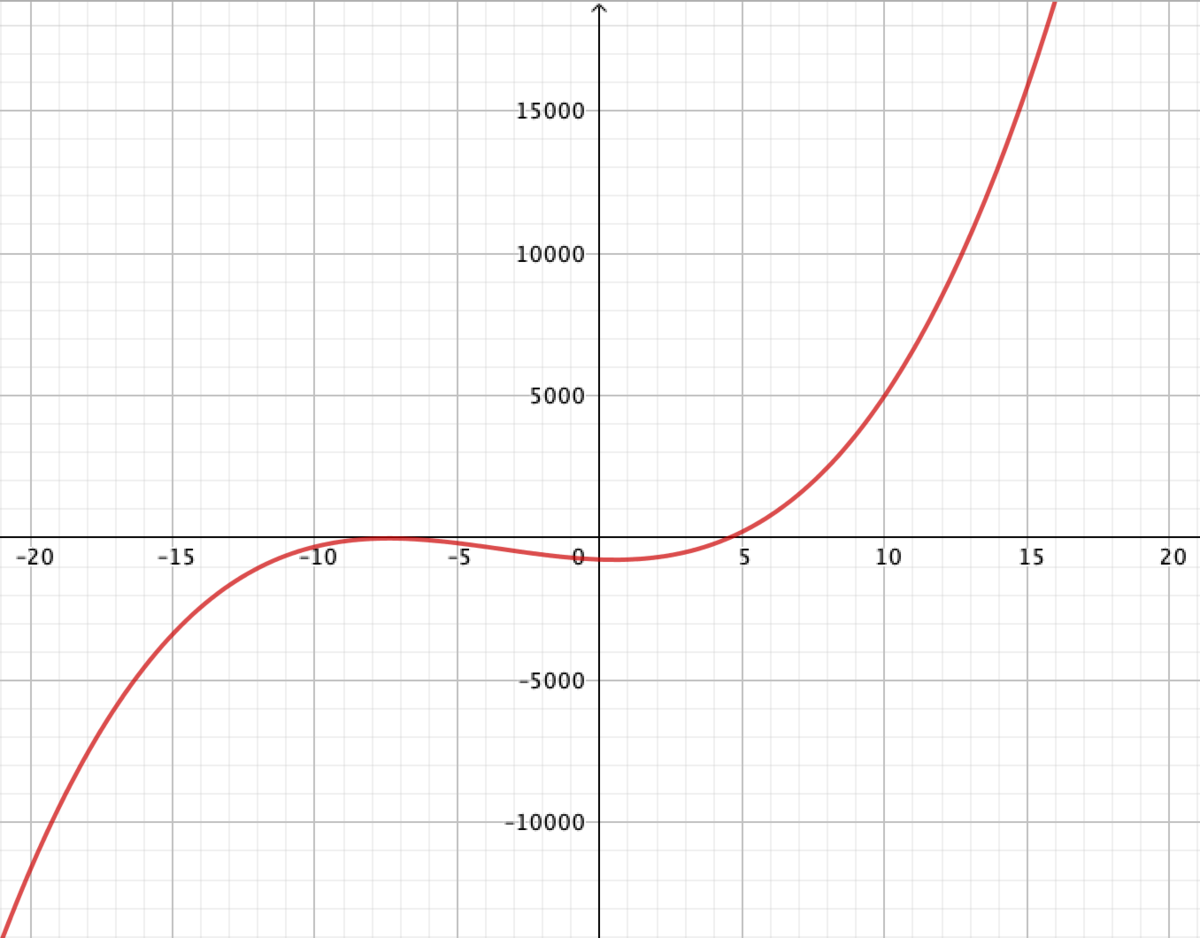
より、
の範囲で
の符号は正に転じるわけですが、実際
より、整数解を持ちません。
 のとき
のとき
を代入すると
となります。 の係数が正のため、
は単調増加します。
ここで
より、整数解を持ちません。
 のとき
のとき
を代入すると
となります。 の係数が正のため、
は単調増加します。
ここで
より、整数解を持ちません。
以上から、すべての なる
に対して、条件を満たす整数
は存在しないことがわかります。
よって、式 には条件を満たす整数解がないことが示されました。(終わり)
おわりに
無事に4-4の問題を解くことができました。
方法は基本的には3-3のときと同じでしたが、 の解が整数かどうかの判定については、3-3の方法と少し異なりました。今回使った方法であれば、
の次数は関係ないので、5-5以降の問題でもそのまま使えるかもしれません。
tsujimotterは正直なところ、4-4の問題が解けるものだとは思っていませんでした。だから、二世さんから「できた」と言われたときは心底驚きました。
私自身は2桁, 3桁の結果で満足してしまっていて、その先をやろうとは思いませんでした。これ以降の問題では4次方程式等の高次の多項式が出てくるのでできないだろうと、安直に考えてしまっていたわけです。ところが、実際にやってみたらできてしまったわけですね。
取り組んでもいないのに「できない」なんて簡単にいうもんじゃないと反省しました。私自身はこれまでも、自分で問題に取り組むことを面倒臭がり、安易に答えを求めたがる傾向がありました。今回の問題を通して、実際に取り組むということの重要性を実感しました。そういう経緯もあって、この問題はぜひ紹介したいなと思ったわけです。
これまで解決できた問題を整理すると、次の図のようになります。
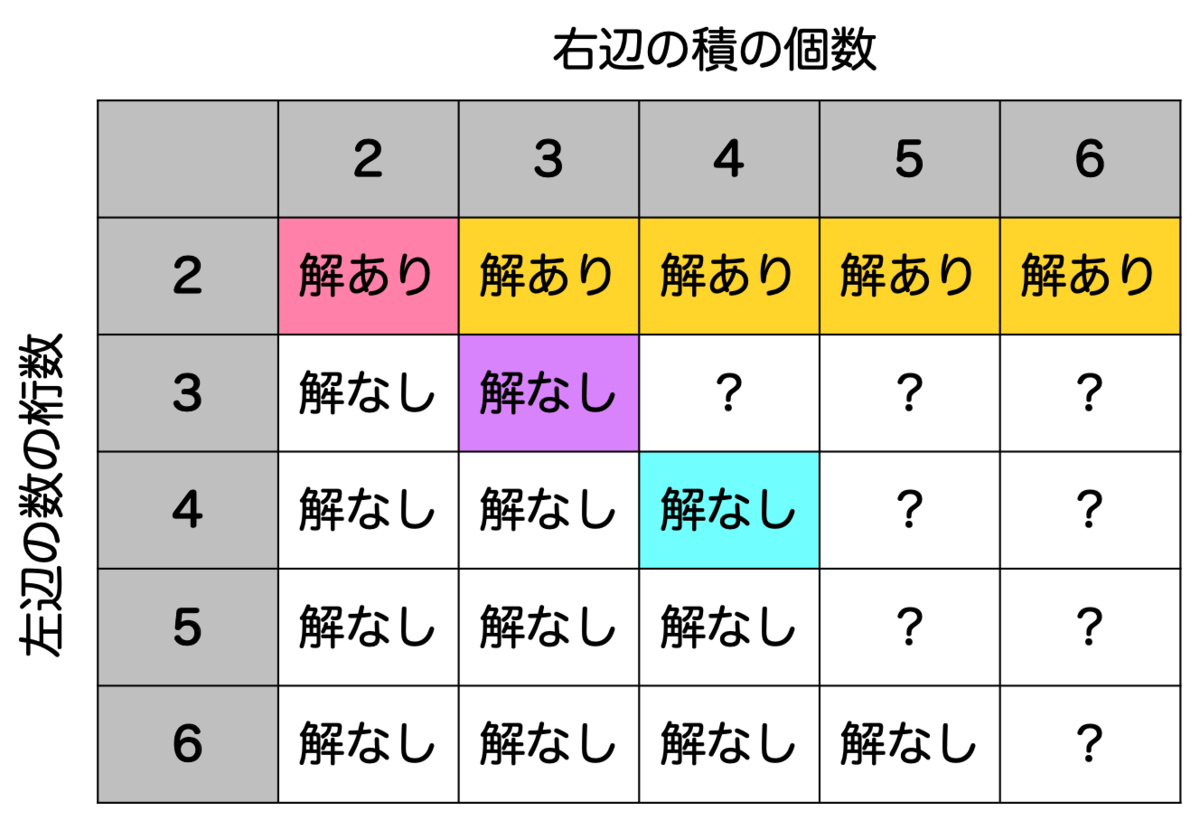
対角成分の問題は 2-2, 3-3, 4-4 まで解決することができましたが、この先も同様の方法で解決できるかもしれません。
気になるのは、3, 4行目の右側の部分ですね。これについてはまた異なる手法が必要になるのでしょうか。
また何か進んだら書きたいと思います。
それでは、今日はこの辺で。
*1:こちらが実際に送ってもらった解答です。
