「」を示す問題が2003年の東大入試で出題されました。これは有名なのでみなさん良くご存じかと思いますが、一方で以下の動画のような解法はご存知でしょうか?
たいへん面白い解法なので、まずは一度ご覧いただきたいです。動画の解説もとても丁寧です。今回の記事はこの動画の内容を前提としてお話したいと思います。
動画の概要欄にもリンクが載っていますが、Yahoo知恵袋の以下の質問の「その他の回答」に載っていた回答が元ネタだそうです。
detail.chiebukuro.yahoo.co.jp
元ネタの人はどうやって発見したんでしょうね。いやー不思議です。
今回私が考えたいのは、いったいどうしてこんな解法が存在するのであろうかということです。登場するパラメータが絶妙なバランスで構成されていて、このような解法が存在すること自体が非自明です。
今回はその背景にある理屈を整数論的に分析してみたいと思います。最後まで読んでいただければ、実は動画で紹介された という数が、いかに特別な数であったか分かるかと思います。
それではぜひ最後までお付き合いください!
ペル方程式とピタゴラス数
今回の問題設定を図示してみると、以下のようになります。
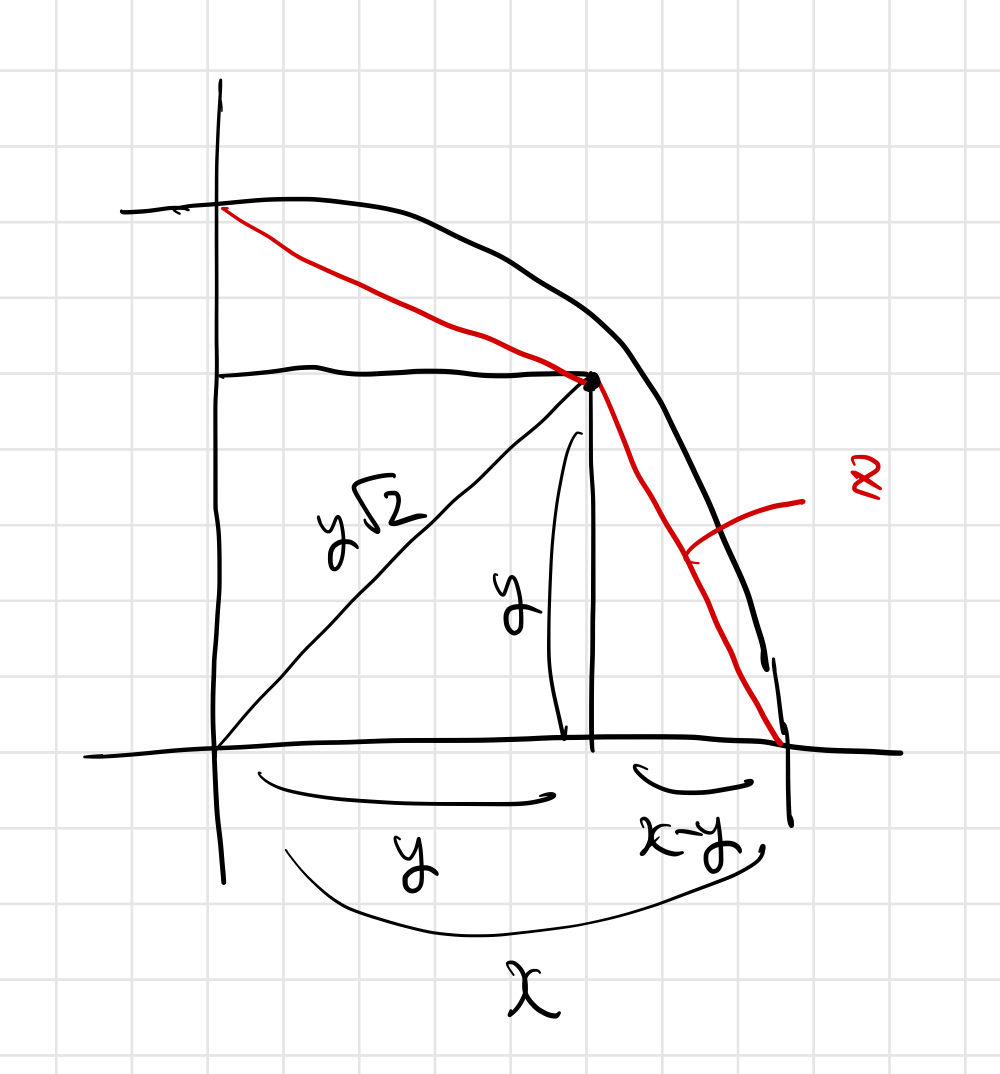
が円の半径の長さで、
は正方形の一辺の長さです。ここで「うまい
を選ぶ」と、
の部分が簡単になって、円周率の近似値が得られると言う話ですね。実際、動画の方法では
を選んでいました。
ここで をいかに選ぶかというのが重要なのですが、さしあたって 2つポイント があります。
一辺の長さが の正方形の対角線の長さ
が、円の半径
より小さく、なるべく近い値をとることが1つめのポイントです。実際、動画の中では
を満たす整数 を選んでいました。このような方程式を ペル方程式 と言います。
ペル方程式 は
の最良近似
を与えるという性質もあり、「なるべく近い値をとる」という目的に合致するチョイスですね。
ペル方程式 には無数の解があって、小さい方から並べるとこのようになります:
は3番目に小さな解にあたります。
さて、単にペル方程式の解であるというだけでなく、さらに ピタゴラス数 が絡んでくるというのが2つめのポイントです。
図の赤い線の長さを とすると、辺の長さが
の直角三角形が出てきます。この斜辺の長さ
が整数であるというのです。整数だから円周率の近似が計算しやすい(中学生にも計算できる)というわけですね。
長さが整数であるような直角三角形の3辺の組をピタゴラス数といいます。特に、今回のように3辺の長さが互いに素になっているものを原始的ピタゴラス数といいます。
まとめると、今回の整数 の組は、次のような条件を満たすペアだったというわけですね!
- (ペル方程式)
- (原始的ピタゴラス数)
なお「原始的」であることは必然的な条件です。
というのも、ペル方程式の解である時点で となります(公約数
をとると仮定すると、
となる)。さらに、
ですし、ピタゴラス数の条件
より
であることが言えるからです。
よって、原始的ピタゴラス数だけを考えれば十分と言うことになります。
このような整数の組はどれぐらいあるのか?
ここで気になってくるのは、上のような条件を満たす正の整数 の組はどれぐらいあるのだろうか、という問題です。
ペル方程式には無限個の解がありますし、原始的ピタゴラス数も無限に存在するので、他にもこのような組み合わせがあっても良さそうですよね。
ところが、大変面白いことに の範囲では、そのような組は
しか存在しないのです。というか、それを 証明することができました。今回はその証明を紹介したいと思います。
は奇跡のペアだった というわけですね。
証明のための最初のステップは、原始的ピタゴラス数の一般論を用いることです。
が原始的ピタゴラス数ということで、
のいずれか一方は偶数、もう一方は奇数になります。どちらが偶数か特定しましょう。
ペル方程式 より、
なので
は奇数です。よって
は奇数です。
は奇数より
おくと
となりますが、ここから
は偶数であるとわかります。
以上により、 が奇数、
が偶数とわかりました。
原始的ピタゴラス数の一般論より、 は偶奇の異なる互いに素な整数
を用いて
と表せます。 が偶数であることを反映して、
としています。
この条件とペル方程式 を同時に満たすような
を決定すれば良いわけです。
だからといって、単純に代入して
を満たす整数 を求めようとすると泥沼になりそうです。実際、これは4次の代数曲線の整数点を求める問題となり、一筋縄では行かなそうです。
「どうにかして解が既知である方程式に帰着できないか」と考えていたところ、@kunne_isepo さんより解決のヒントをいただくことができました。上記の整数問題を
の整数解の問題に帰着することができるのです。
Tomohiro Yamadaさんのホームページによると、式 の方程式の整数解は
の8つ(符号はすべての組み合わせを考える)のみであることが、Ljunggren(1942年)により証明されているのだそうです。
それでは、式 に帰着させることを考えましょう。
このような を用いて、
とおくと、 は
を満たす。
どうやって、このような変換を見つけたのかと思うかもしれません。
元々、式 の整数解
が満たす
によるパラメータ表示を求める方法があります。原始的ピタゴラス数のときと同じ要領なのですが、@kunne_isepo さんに教えていただいたのがその方法でした。
この手順を逆に辿ることで、上の変換が得られるという寸法です。
それでは、上のグレー色の枠内の主張を示しましょう。
まず
は、元々ピタゴラスの式が成り立つように与えられたパラメータです。すなわち
が成り立ちます。左辺の変数を用いて言い換えると
が成り立つというわけですね。
式 と
を
に代入し、以下のように計算します:
よって、 が成り立つことが示されました。
これにてグレー色の枠内の主張の証明が完結し、問題を に帰着することができました。
この方程式の整数解は
のみであることが知られているので、これらの解に対して、対応する を議論すれば良いでしょう。
のとき
より、
が言えます。
これに対応する円の半径 は
ですが、これは に反します。したがって、このケースは不適です。
のとき
より、
が言えます。
これに対応する円の半径 は
であり、対応する正方形の一辺の長さ は
となります。
これらは、動画で登場した の組であり、条件を満たすような
はこの組以外は存在しないことが示されました。
せっかくなので、今決定した整数解(正負含む)を曲線
にプロットすると次のようになります:
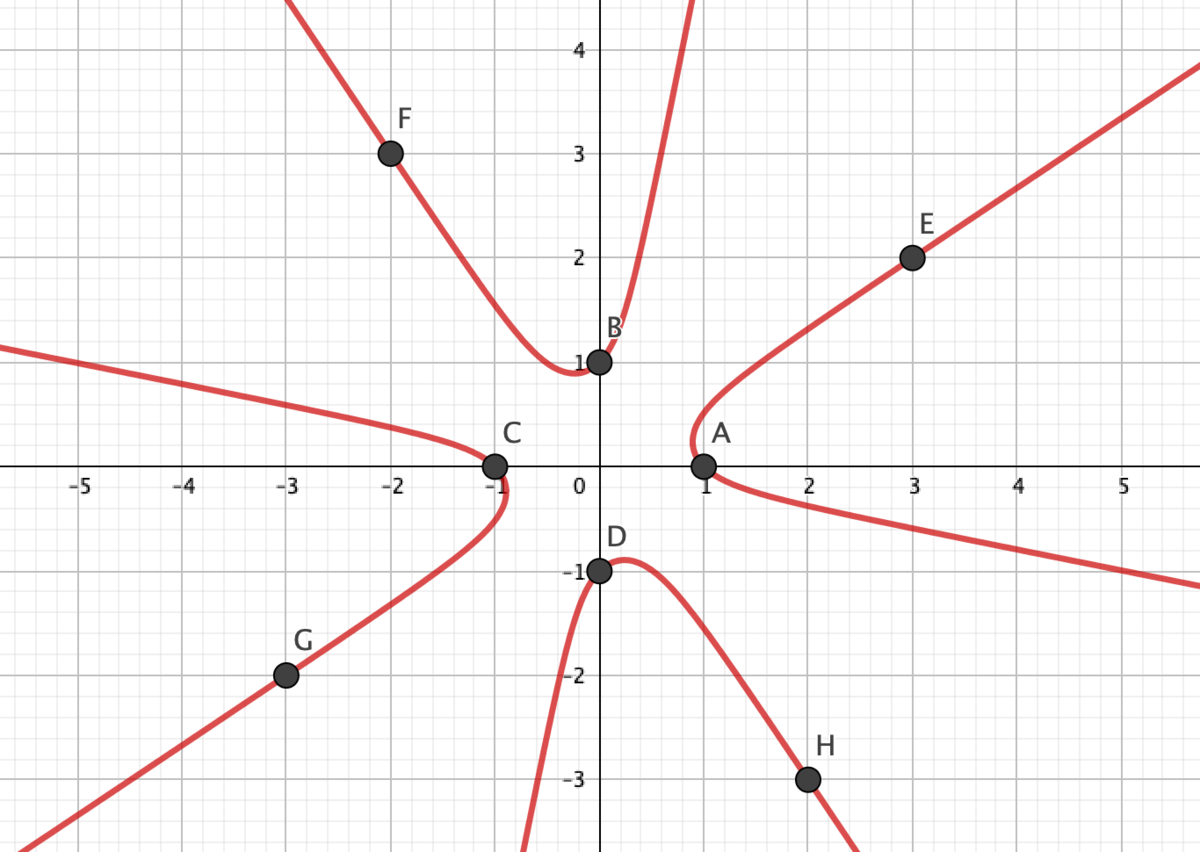
(ちゃんと証明した点が格子点上に乗っていることが確認できたときは興奮しました!)
おわりに
今回の記事では、動画の証明方法を拡張するために、条件を満たす を求めようという記事でした。
そのような には
- (ペル方程式)
- (原始的ピタゴラス数)
という条件が自然に課されます。
このような条件を満たす正整数の組 は、なんと
しか存在しないということが示されました!面白いですね!
個人的には、この問題が
という有名な方程式の整数解に帰着できるというのが面白かったです。
この方程式は実際楕円曲線であり、 とおけばワイエルシュトラスの標準形
に変形できます。
楕円曲線の整数解を求めると言うことが、数学においてどれぐらい有用なのかと言うのは、なかなかピンと来づらいかと思います。色々定理を教わっても、それがどれぐらい重要なのかがわかりづらい。
実際に今回のような応用があることがわかると、その強力さを実感できて面白いですよね。
とすることにより、円周率のマチンの公式というこれまた面白い応用と結びつきます。
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com
というわけで、大変楽しい日曜数学でした。それでは今日はこの辺で!